Izomorfismus obecných grafů a stromů
LAB 05
B4M33PAL - Ing. David Pařil
Příklad
Izomorfizmus Cyklu
Máme dvě neorientované kružnice stejné délky \(k > 2\).
Kolik mezi nimi existuje izomorfismů?
Řešení
Pro kružnici (cyklus) s \(k>2\) obsahuje grupa automorgismů:
1) \(k\) rotací
2) \(k\) zrcadlení (reverzí)
Příklad
Izomorfizmy grafů
Určete počet izomorfismů mezi grafy \(G_1\) a \(G_2\).
Graf \(G_1\)
Graf \(G_2\)
Určete počet izomorfismů mezi grafy \(G_1\) a \(G_2\).
Určete počet izomorfismů mezi grafy \(G_1\) a \(G_2\).
Máme 4 vrcholy stupně 2 a 4 vrcholy stupně 3.
Zvolíme obraz jednoho koncového vrcholu v \(G_2\) - jsou 4 možnosti. Jakmile je zvolen, obraz jeho partnera v páru i všech dalších vrcholů je už jednoznačně určen.
Tedy počet izomorfizmů = 4.
Izomorfizmus
Příklad
Neizomorfní bijekce - Část 1
Kolik je takových bijekcí mezi uzly grafů \(G_1\) a \(G_2\) na obrázku níže, které nejsou izomorfismy?
5
1
2
3
4
a
b
c
d
e
\(G_1\)
\(G_2\)
Řešení
Oba grafy mají stejnou stupňovou posloupnost \(3, 3, 2, 2, 2,\).
Střecha (stupeň 2 sousedící s dvěmi stupni 3) určuje zobrazení \(4 \rightarrow e\).
Vrcholy stupně 3 lze vzájemně zobrazit 2 způsoby (prohození).
Vrcholy stupně 2 se pak jednoznačně přizpůsobí.
5
1
2
3
4
a
b
c
d
e
5
1
2
3
4
a
b
c
d
e
Počet izomorfismů:
Počet bijekcí:
Počet neizomorfismů:
\(2\)
\(5! = 120\)
\(120 - 2 = 118\)
Příklad
Neizomorfní bijekce - Část 2
Kolik je takových bijekcí mezi uzly grafů \(G_1\) a \(G_2\) na obrázku níže, které nejsou izomorfizmy?
3
5
6
8
4
7
1
2
\(G_1\)
e
a
b
c
d
f
g
h
\(G_2\)
Jediný vrchol stupně 7 je pevný.
Tři listy stupně 1 lze libovolně permutovat \(\rightarrow 3! = 6\) možností.
Čtyři vrcholy stupně 2 tvoří dvě nerozlišitelné hrany:
- 4 volby pro první node (např. \(5 \rightarrow g/h/a/b\))
- 2 možnosti prohození druhé hrany
Celkem tedy \(8! - 6 \times 8 = 40320 - 48 = 40272\)
3
5
6
8
4
7
1
2
e
a
b
c
d
f
g
h
Příklad
Neizomorfní bijekce - Část 3
Kolik je takových bijekcí mezi uzly grafů \(G_1\) a \(G_2\) na obrázku níže, které nejsou izomorfizmy?
e
a
b
f
d
c
3
5
4
2
1
6
\(G_1\)
\(G_2\)
Řešení
Oba grafy jsou obyčejný cyklus \(C_6\) \(\rightarrow\) každý vrchol má stupeň 2
Z prvního příkladu již víme, že izomorfismů tedy máme \(2 \cdot 6 = 12\)
Počet bijekcí, které nejsou izomorfismy je tedy \(720-12 = \textbf{708}\)
e
a
b
f
d
c
3
5
4
2
1
6
Příklad
Neizomorfní bijekce - Část 4
Kolik je takových bijekcí mezi uzly grafů \(G_1\) a \(G_2\) na obrázku níže, které nejsou izomorfizmy?
1
2
3
4
5
8
7
6
e
d
b
g
a
c
h
f
\(G_1\)
\(G_2\)
Řešení
Oba grafy jsou izomorfní. Mají stupně:
- \(2\times\) stupeň 5
- \(2\times\) stupeň 2 sousedící s oběma stupni 5
- \(2\times\) stupeň 2 tvořící hrany připojené na jeden ze stupňů 5
1
2
3
4
5
8
7
6
e
d
b
g
a
c
h
f
Oba grafy jsou izomorfní. Mají stupně:
- \(2\times\) stupeň 5
- \(2\times\) stupeň 2 sousedící s oběma stupni 5
- \(2\times\) stupeň 2 tvořící hrany připojené na jeden ze stupňů 5
1
2
3
4
5
8
7
6
e
d
b
g
a
c
h
f
Automorfismus musí zachovat tyto třídy, máme následující možnosti:
- 2️⃣ prohodit či neprohodit \(\textcolor{red}4 \leftrightarrow \textcolor{red}5\)
- 2️⃣ prohodit či neprohodit \(2 \leftrightarrow 7\)
- 2️⃣ prohodit či neprohodit \(1 \leftrightarrow 6\)
- 2️⃣ prohodit či neprohodit \(3 \leftrightarrow 8\)
1
2
3
4
5
8
7
6
e
d
b
g
a
c
h
f
Automorfismus musí zachovat tyto třídy, máme následující možnosti:
- 2️⃣ prohodit či neprohodit \(\textcolor{red}4 \leftrightarrow \textcolor{red}5\)
- 2️⃣ prohodit či neprohodit \(2 \leftrightarrow 7\)
- 2️⃣ prohodit či neprohodit \(1 \leftrightarrow 6\)
- 2️⃣ prohodit či neprohodit \(3 \leftrightarrow 8\)
Neizomorfismů je tedy: \(8! - 2 \cdot 2 \cdot 2 \cdot 2 = 40320 - 16 = \textbf{40304} \)
Příklad
Asymptotická složitost speciálního izomorfismu
Máme dány dva neorientované grafy, každý obsahuje právě \(n\) uzlů a oba grafy mají skóre
$$(n─1, n─2, n─3, n─4, ..., \frac n 2+1, \frac n 2, \frac n 2, \frac n 2─1, \frac n 2─2, ..., 3, 2, 1)$$
to jest skoro všechny uzly grafu mají navzájem různý stupeň, s výjimkou dvou uzlů, které mají stejný stupeň \(\frac n 2\).
Jaká bude asymptotická složitost ověření izomorfizmu těchto dvou grafů v závislosti na hodnotě \(n\)?
Řešení
Stupně jsou téměř všechny různé, takže korespondence vrcholů je daná jednoznačně pro \(n−2\) vrcholů. Nejednoznačné zůstávají jen dva vrcholy.
Pro jednoznačné přiřazení stačí ověřit, že se každá hrana \(G_1\) promítá na hranu \(G_2\):
$$m = \frac 1 2 \sum deg = \frac 1 2 \left( \sum_{k=1}^{n-1} k + \frac n 2 \right) = \frac 1 2 \left(\frac{n(n-1)}{2} + \frac n 2 \right) = \frac{n^2}{4} = O(n^2)$$
Dvě možnosti přiřazení jsou jen konstantní faktor \(\rightarrow\) asymptotická složitost testu izomorfismu je \(O(n^2)\)
Příklad
počet izomorfizmů s využitím deskriptorů
Předveďte postup určování počtu izomorfizmů pro následující dvojice grafů s využitím deskriptorů:
$$\begin{aligned} D_1(G,x) &= \deg_G(x),\\[2pt] D_2(G,x) &= \bigl[d_j(x) :\; j=1,2,\ldots,\max\{\deg_G(x): x\in V(G)\}\bigr],\\ &\quad \text{kde } d_j(x)=\bigl|\{\, y : y \text{ sousedí s } x \text{ a } \deg_G(y)=j \,\}\bigr|. \end{aligned}$$
Předveďte postup určování počtu izomorfizmů pro následující dvojice grafů s využitím deskriptorů:
$$\begin{aligned} D_1(G,x) &= \deg_G(x),\\[2pt] D_2(G,x) &= \bigl[d_j(x) :\; j=1,2,\ldots,\max\{\deg_G(x): x\in V(G)\}\bigr],\\ &\quad \text{kde } d_j(x)=\bigl|\{\, y : y \text{ sousedí s } x \text{ a } \deg_G(y)=j \,\}\bigr|. \end{aligned}$$
5
1
2
3
4
a
b
c
d
e
\(G_1\)
\(G_2\)
5
1
2
3
4
a
b
c
d
e
| x | D1(G1,x) | D2(G1,x) |
|---|---|---|
| 1 | 2 | [0,1,1] |
| 2 | 2 | [0,1,1] |
| 3 | 3 | [0,2,1] |
| 4 | 2 | [0,0,2] |
| 5 | 3 | [0,2,1] |
| x | D1(G1,x) | D2(G1,x) |
|---|---|---|
| a | 3 | [0,2,1] |
| b | 2 | [0,1,1] |
| c | 2 | [0,1,1] |
| d | 3 | [0,2,1] |
| e | 2 | [0,0,2] |
| x | D1(G1,x) | D2(G1,x) |
|---|---|---|
| 1 | 2 | [0,1,1] |
| 2 | 2 | [0,1,1] |
| 3 | 3 | [0,2,1] |
| 4 | 2 | [0,0,2] |
| 5 | 3 | [0,2,1] |
| x | D1(G1,x) | D2(G1,x) |
|---|---|---|
| a | 3 | [0,2,1] |
| b | 2 | [0,1,1] |
| c | 2 | [0,1,1] |
| d | 3 | [0,2,1] |
| e | 2 | [0,0,2] |
1) Z našich tabulek vyjdou shodné třídy:
-
{4}↔{e} \{4\}\leftrightarrow\{e\}\(\lbrace 4 \rbrace \leftrightarrow \lbrace e \rbrace \) (vektor [0,0,2][0,0,2][0,0,2]),
-
\(\lbrace 3,5 \rbrace \leftrightarrow \lbrace a,d \rbrace \) (vektor [0,2,1][0,2,1][0,2,1]),
-
{3,5}↔{a,d} \{3,5\}\leftrightar
-
{1,2}↔{b,c} \{1,2\}\leftrightarrow\{b,c\}\(\lbrace 1,2 \rbrace \leftrightarrow \lbrace b,c \rbrace \) (vektor [0,1,1][0,1,1][0,1,1]).
2) Dopočítej počet izomorfismů:
- 1️⃣ \(\lbrace 4 \rbrace \rightarrow \lbrace e \rbrace \)
- 2️⃣\(\lbrace 3,5 \rbrace \rightarrow \lbrace a,d \rbrace \) lze prohodit
- 1️⃣\(\lbrace 1,2 \rbrace \rightarrow \lbrace b,c \rbrace \) jednoznačné
Příklad
Izomorfní iluze
Popište, jak budete co nejefektivněji rozhodovat, zda dva uvedené grafy jsou nebo nejsou izomorfní.
Rozložme podle \(D_1\) i podle \(D_2\) (počty vrcholů ve vzdálenostech 1–3)
| x | D1(G1,x) | D2(G1,x) |
|---|---|---|
| 1 |
4 | 4,6,4 |
| 2 | 4 | 4,6,4 |
| 3 | 4 | 4,6,4 |
| 4 | 6 | 6,8,0 |
| 5 | 6 | 6,8,0 |
| 6 | 6 | 6,8,0 |
| 7 | 2 | 2,6,6 |
| 8 | 2 | 2,6,6 |
| 9 | 2 | 2,6,6 |
| 10 | 4 | 4,6,4 |
| 11 | 4 | 4,6,4 |
| 12 | 4 | 4,6,4 |
| 13 | 2 | 2,6,6 |
| 14 | 2 | 2,6,6 |
| 15 | 2 | 2,6,6 |
| x | D1(G2,x) | D2(G2,x) |
|---|---|---|
| 1 | 4 | 4,6,4 |
| 2 | 4 | 4,6,4 |
| 3 | 4 | 4,6,4 |
| 4 | 6 | 6,8,0 |
| 5 | 6 | 6,8,0 |
| 6 | 6 | 6,8,0 |
| 7 | 2 | 2,6,6 |
| 8 | 2 | 2,6,6 |
| 9 | 2 | 2,6,6 |
| 10 | 4 | 4,6,4 |
| 11 | 4 | 4,6,4 |
| 12 | 4 | 4,6,4 |
| 13 | 2 | 2,6,6 |
| 14 | 2 | 2,6,6 |
| 15 | 2 | 2,6,6 |
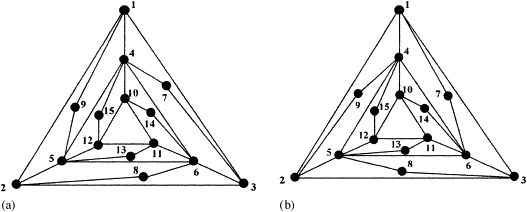

Všechno je stejný 😎👍
Přesto grafy nejsou izomorfní 😭
Vpravo existuje 6-cyklus obsahující dva vrcholy stupně 2 ve vzdálenosti 2
Vlevo existuje 6-cyklus obsahující dva vrcholy stupně 2 ve vzdálenosti 3
Grafy nemohou být izomorfní!
Nyní bychom mohli vyzkoušet některé další invariantní indukující funkce, jako např. stupně uzlů v určité vzdálenosti od x, excentricitu x, excentricitu sousedů x, počet trojúhelníků incidentních s x, počet cyklů o délce 4 incidentních s x atd...
Žádná z nich by významně nezvýšila počet různých rodin uzlů v grafech.
Tento příklad byl vybrán k demonstraci obtížnosti posouzení izomorfismu.
Příklad
Certifikovaný Graf
Po sestavení certifikátu stromu odpovídá každému uzlu stromu určitý podřetězec konečného certifikátu.
Sestavte certifikát každého ze 4 stromů a určete, které jeho podřetězce odpovídají jednotlivým uzlům stromu.
a)
01
01
01
01
01
01
0011
01
01
0011
000111
000111
b)
01
01
01
01
01
01
01
01
0010101010101011
c)
01
01
01
01
01
01
01
0011
0011
001011
00010110011011
d)
01
01
01
01
01
01
01
01
01
01
01
0001010110010101100111
01
00101011
0011
00101011
Příklad
De-Certifikovaný Graf
Rekonstruujte strom z certifikátu:
a) 0011 b) 0001 0110 0101 0111 c) 0001 0110 0101 1001 0111 d) 0000 0101 1100 1110 0001 0111 0111
(mezery a barvy jsou pouze pro zvýšení čitelnosti)

a) 0011
Nevalidní certifikát 😭
Existuje jenom jeden strom s 2 uzly a jeho certifikát je 0101.
b) 0001 0110 0101 0111
Nevalidní certifikát 😭
c) 0001 0110 0101 1001 0111
d) 0000 0101 1100 1110 0001 0111 0111
Příklad
Listí z Certifikátu 🍃
Je dán certifikát stromu.
Vysvětlete, jak určíme počet listů tohoto stromu (bez kompletní rekonstrukce stromu).
0101011010110100100101010100101010010010100101010010101001001010010100101010010100110010101001010010010100101010010100101010010100010010100101010010100101001010100101001010010100101001010100100101010010101010101001010010100101010100101010101010101010110101010101100101011010010101010101001010110100101001010011010010101010101010010100101010100101010010101001010100101010011011010100101010010010100101010010100101011001010010101010100101010010101010010101010010101010010101010100101010101010010101010010100101010100101010010101001010101001010101001010101010010100101001001010101010101010101010101010101101010101101010101010101010101010101001010100101010010101010010110101100110010100101101001010101001010110110101001010101001101001010101011010101010010011010101010010101101010011101010101001
Podle algoritmu pro konstrukci certifikátu jsou všechny listy označeny řetězcem 01.
Popisky interních uzlů se skládají z alespoň 4 symbolů a tento popisek obsahuje jako podřetězce všechny popisky podstromů s kořeny v X.
Proto je korespondence mezi podřetězci 01 v certifikátu stromu a listy stromu bijekcí.
Počet podřetězců 01 v certifikátu se rovná počtu listů ve stromu.
Řešení
Příklad
Maximální Stupeň Uzlu z Certifikátu
Je dán certifikát stromu.
Vysvětlete, jak určíme maximální stupeň uzlu tohoto stromu (bez kompletní rekonstrukce stromu).
Co je certifikát: Řetězec z nul a jedniček, který kóduje průchod stromem do hloubky (DFS).
0 znamená „jdu po nové hraně k dítěti“
1 znamená „vracím se o jednu hranu zpět“
Řešení
Dekódování (rekonstrukce stromu z certifikátu):
Pořadí dětí nemusíme znát (narozdíl od kódování).
Stačí postupovat sekvenčně:
-
když čtu 0, nakreslím novou hranu od aktuálního uzlu k novému vrcholu a přesunu se do něj;
-
když čtu 1, vrátím se po jedné hraně zpět směrem ke středu (k rodiči).
Řešení
Dekódování (rekonstrukce stromu z certifikátu):
Pořadí dětí nemusíme znát (narozdíl od kódování).
Stačí postupovat sekvenčně:
-
když čtu 0, nakreslím novou hranu od aktuálního uzlu k novému vrcholu a přesunu se do něj;
-
když čtu 1, vrátím se po jedné hraně zpět směrem ke středu (k rodiči).
Zásobník (stack):
Během dekódování si vedeme zásobník navštívených uzlů.
Když z uzlu odcházíme naposledy (přečtu 1 a už pro něj není další 0), uzel „zavřeme“ a odebereme ho ze zásobníku.
Stupeň (degree) uzlu:
Stačí si u každého uzlu počítat, kolikrát jsme v něm byli, zatímco je na zásobníku.
Ve chvíli, kdy se uzel zavře, je počet těchto návštěv rovný jeho stupni.
Příklad
Certifikát T(1,3)
Strom typu \(T(1,3)\) obsahuje uzly pouze stupně \(1\) nebo \(3\).
Popište neformálně jak bude vypadat certifikát takového stromu a navrhněte algoritmus, který pomocí certifikátu ověří, zda strom je skutečně typu \(T(1,3)\).
Kořen:
-
je-li centroid jeden, kořen má 3 děti ⇒ celý certifikát je
-
jsou-li centroidy dva, certifikát je konkatenace dvou top-bloků S S, přičemž každý z nich je typu 0 S S 1.
Řešení
Sleaf -> 01
Sint -> 0 S S 1
R1 -> 0 S S S 1 (jediný centroid)
R2 -> Sint Sint (dva centroidy)
CERT -> R1 | R2