kombinatorika, Grayovy kódy

LAB 06

B4M33PAL - Ing. David Pařil

Příklad

Rank Permutace

Určete rank permutace:

$(4, 2, 5, 1, 3)$
$(5, 6, 3, 4, 1, 2)$

Řešení

Lexikografický rank od nuly

Lehmerův kód

$4!\cdot$

$3!\cdot$

$2!\cdot$

$1!\cdot$

$0!\cdot$

$=72$

$=6$

$=4$

$=0$

$=82$

Rank permutace

Lexikografické pořadí:

Řešení

$=592$

$5!\cdot$

$3!\cdot$

$4!\cdot$

$2!\cdot$

$1!\cdot$

$0!\cdot$

$=480$

$=96$

$=12$

$=4$

$=0$

Lexikografické pořadí:

Příklad

Permutace z Ranku

Najděte permutaci množiny $\lbrace1, 2, 3, 4, 5, 6\rbrace$, jejiž rank je:

$111$
$222$

Řešení

$=111$

$5!\cdot$

$3!\cdot$

$4!\cdot$

$2!\cdot$

$1!\cdot$

$0!\cdot$

$=0$

$=96$

$=12$

$=2$

$=1$

$=0$

$\rightarrow\frac{111}{120}$

$\rightarrow\frac{111}{24}$

$\rightarrow\frac{15}{6}$

$\rightarrow\frac{3}{2}$

$\rightarrow\frac{1}{1}$

$\rightarrow\text{vždy } 0$

Lexikografické pořadí:

Řešení

$=222$

$5!\cdot$

$3!\cdot$

$4!\cdot$

$2!\cdot$

$1!\cdot$

$0!\cdot$

$=120$

$=96$

$=6$

$=0$

$\rightarrow\frac{222}{120}$

$\rightarrow\frac{102}{24}$

$\rightarrow\frac{6}{6}$

$\rightarrow\frac{0}{2}$

$\rightarrow\frac{0}{1}$

$\rightarrow\text{vždy } 0$

Lexikografické pořadí:

Příklad

Rank podmnožin

Určete rank 3-prvkové podmnožiny:

$\lbrace 2, 4, 6\rbrace$
$\lbrace 2, 5, 6 \rbrace$

množiny $\lbrace1, 2, 3, 4, 5, 6, 7\rbrace$

Řešení

$\lbrace 1, 2, 3\rbrace$
$\lbrace 1, 2, 4\rbrace$
$\lbrace 1, 2, 5\rbrace$
$\lbrace 1, 2, 6\rbrace$
$\lbrace 1, 2, 7\rbrace$
$\lbrace 1, 3, 4\rbrace$
$\lbrace 1, 3, 5\rbrace$
$\lbrace 1, 3, 6\rbrace$
$\lbrace 1, 3, 7\rbrace$
$\lbrace 1, 4, 5\rbrace$
$\lbrace 1, 4, 6\rbrace$
$\lbrace 1, 4, 7\rbrace$
$\lbrace 1, 5, 6\rbrace$
$\lbrace 1, 5, 7\rbrace$
$\lbrace 1, 6, 7\rbrace$
$\lbrace 2, 3, 4\rbrace$
$\lbrace 2, 3, 5\rbrace$
$\lbrace 2, 3, 6\rbrace$
$\lbrace 2, 3, 7\rbrace$
$\lbrace 2, 4, 5\rbrace$
$\lbrace 2, 4, 6\rbrace$
$\lbrace 2, 4, 7\rbrace$
$\lbrace 2, 5, 6\rbrace$
$\lbrace 2, 5, 7\rbrace$
$\lbrace 2, 6, 7\rbrace$
$\lbrace 3, 4, 5\rbrace$
$\lbrace 3, 4, 6\rbrace$
$\lbrace 3, 4, 7\rbrace$
$\lbrace 3, 5, 6\rbrace$
$\lbrace 3, 5, 7\rbrace$
$\lbrace 3, 6, 7\rbrace$
$\lbrace 4, 5, 6\rbrace$
$\lbrace 4, 5, 7\rbrace$
$\lbrace 4, 6, 7\rbrace$
$\lbrace 5, 6, 7\rbrace$

Hledám rank podmnožiny $\lbrace 2, 4, 6\rbrace$

Kolik čísel je na pozici 1 menších jak 2?
Kolik čísel je na pozici 2 menších jak 4?
Kolik čísel je na pozici 3 menších jak 6?

Čísel, co začínají 1 je $\binom{6}{2}$.
Čísel, co pokračují 3kou je $4$, protože zbývají už jen 4, 5, 6, 7.
Pouze číslo 5 může být na poslední pozici menší než 6.

$\Rightarrow 15 + 4 + 1 = \bold{\textcolor{orange}{20}}$

Řešení

Hledám rank podmnožiny $\lbrace 2, 5, 6\rbrace$

Kolik čísel je na pozici 1 menších jak 2?
Kolik čísel je na pozici 2 menších jak 5?
Kolik čísel je na pozici 3 menších jak 6?

Čísel, co začínají 1 je $\binom{6}{2}$.
Čísel, co pokračují 3kou nebo 4kou je $7$
- $3 \Rightarrow 4, 5, 6, 7$
- $4 \Rightarrow 5, 6, 7$
Žádné číslo nemůže být na poslední pozici menší než 6.

$\Rightarrow 15 + 7 + 0 = \bold{\textcolor{orange}{22}}$

Řešení

Hledám rank podmnožiny $\lbrace 2, 5, 6\rbrace$

$2$

$3$

$4$

$5$

$6$

$1$

$0$

$\_$

$\binom 6 2$

$\binom 4 1$

$\binom 3 1$

$\binom{7-\textcolor{red}{1}}{3-\textcolor{purple}{1}}$

$\binom{7-\textcolor{green}{3}}{3-\textcolor{purple}{2}}$

$\binom{7-\textcolor{green}{4}}{3-\textcolor{purple}{2}}$

Obecně:

$$\binom{n-a_{ij}}{k-\textcolor{purple}{j}}$$

Příklad

Podmnožina z ranku

Rank 4-prvkové podmnožiny $X$ množiny $\lbrace 1, 2, 3, 4, 5, 6, 7, 8\rbrace$ je právě:

A) $55$

B) $35$

Určete $X$

Řešení

Vezmeme lexikografický rank od nuly a „rozbalíme“ ho po blocích.

Pro $n=8$, $k=4$ mají bloky podle 1. prvku velikosti $\binom{8-a_1}{3}$.
Uvnitř bloku (daný $a_1$) mají bloky podle 2. prvku velikost $\binom{8-a_2}{2}$, pak $\binom{8-a_3}{1}$ a nakonec je 1 prvek.

A) rank = 55

$\binom 7 3 = 35$ pro $a_1 = 1$
$\binom 6 3 = 20$ pro $a_1 = 2$
$35+20 = 55 \Rightarrow a_1 = 3$ a zbytek $r = 0$ v tomto bloku
$\binom 4 2 = 6$ pro $a_2 = 4$ $\Rightarrow$ přeteklo $\Rightarrow$ první prvek
$\binom 3 1 = 3$ pro $a_3 = 5$ $\Rightarrow$ přeteklo $\Rightarrow$ první prvek
Poslední prvek je první možný $a_4 = 6$

$X = \lbrace 3,4,5,6 \rbrace$

Řešení

Vezmeme lexikografický rank od nuly a „rozbalíme“ ho po blocích.

A) rank = 35

$\binom 7 3 = 35$ pro $a_1 = 1$
$35 = 35 \Rightarrow a_1 = 2$ a zbytek $r = 0$ v tomto bloku
$\binom 5 2 = 10$ pro $a_2 = 3$ $\Rightarrow$ přeteklo $\Rightarrow$ první prvek
$\binom 4 1 = 4$ pro $a_3 = 4$ $\Rightarrow$ přeteklo $\Rightarrow$ první prvek
Poslední prvek je první možný $a_4 = 5$

$X = \lbrace 2,3,4,5 \rbrace$

Příklad

Generátor zcela náhodných slov (bez opakování)

Je dána množina malých písmen $P = \lbrace a, b, c, ..., z \rbrace$ bez diakritiky. Máme vygenerovat tabulku $T$ s 8 sloupci, jejíž každý řádek bude obsahovat jednu 8-prvkovou podmnožinu množiny $P$ tak, že každá buňka na řádku bude obsahovat právě jeden znak. Tabulka bude obsahovat všechny možné navzájem různé 8-prvkové podmnožiny $P$ a žádná podmnožina se v $T$ nebude opakovat. Určete, jak bude tabulka velká a zda ji váš počítač bude moci vyplnit během 1 sec.

Řešení

Počet řádků:

Počet buněk:

Stihneme to za $1s$?

¯\_(ツ)_/¯

Můj laptop v pythonu s itertools: $0.141s$

$$1562275 \cdot 8 = 12\,498\,200 \text{ buněk}$$

$$\binom {26} 8\ = \frac{26!}{8! \cdot (26-8)!} = 1\,562\,275 \text{ řádků}$$

To je 12.5 MB paměti 😯

Příklad

Rekurze 101

Napište pseudokód funkce, která vypíše všechny neprázdné podmnožiny množiny

$$\lbrace 0, 1, 2, ..., n─1 \rbrace$$

Řešení

Systematicky "beru/neberu" každý prvek:

subset = []

def dfs(i):
    if i == n:
        if subset:  # neprázdné
            print(subset)
        return
    # 1) nevzít i
    dfs(i + 1)
    # 2) vzít i
    subset.append(i)
    dfs(i + 1)
    subset.pop()

dfs(0)

Příklad

Přívětivé permutace

Mějme permutace množiny $M = \lbrace 1, 2, 3, ..., n \rbrace$, $n > 4$.

Permutaci $p$ této množiny prohlásíme za přívětivou, pokud platí:

$$\begin{align*} p(3) &\in \lbrace 3, n \rbrace \\ p(n) &\in \lbrace 3, n \rbrace\\ p(1) &= 1 \\ p(2) &= 2 \\ p(i) &\in \lbrace 4, ..., n−1 \rbrace \text{ pro } i = 4, ..., n−1 \end{align*}$$

Určete počet přívětivých permutací množiny M.

Řešení

Máme pěvně dané:

$p(1) = 1$
$p(2) = 2$

Hodnoty $3$ a $n$ se smějí objevit jen na pozicích $3$ a $n$

Na pozicích $4, ..., n-1$ tedy mohou být jen čísla $4, ..., n-1$ a to právě 1×

Přívětivé permutace:

$$\begin{align*} p(3) &\in \lbrace 3, n \rbrace \\ p(n) &\in \lbrace 3, n \rbrace\\ p(1) &= 1 \\ p(2) &= 2 \\ p(i) &\in \lbrace 4, ..., n−1 \rbrace \text{ pro } i = 4, ..., n−1 \end{align*}$$

Z toho plyne:

dvojice $(p(3), p(n))$ je permutace $(3, n)$ $\Rightarrow$ 2 možnosti.
zbytek je libovolná permutace množiny $\lbrace 4, ...., n-1 \rbrace$ o velikosti $n-4$

Celkem:

$2 \cdot (n-4)!$ přívětivých permutací.

Příklad

Generování kódu pana šedého :)

Předpokládejme, že každý prvek Gray code $G_n$, jímž je n-tice nul a jedniček, bude uložen v poli znaků o délce $n$.

Napište pseudokód rekurzivní funkce, která pro dané $n$ vygeneruje a vypíše celý Gray code $G_n$.

Řešení podle Pata

Pat chodí na přednášky a proto zná

Lemma 1:

Mějme:

$0 \leq r \leq 2^n -1$
$B = b_{n-1}, ..., b_0$ je binární kód $r$
$G=g_{n-1}, ..., g_0$ je Grayův kód $r$

Pak pro všechna $j \in \lbrace 0, 1, ..., n-1 \rbrace$

$$g_j = (b_j + b_{j+1})\%2$$

Zdroj obrázku: https://patamat.cz/

Využití pro účely výuky na ČVUT FEL dle AutZ §31a

Řešení podle Pata

Zdroj obrázku: https://patamat.cz/

Využití pro účely výuky na ČVUT FEL dle AutZ §31a

def gray_code(n):
    for r in range(1 << n):
        g = r ^ (r >> 1)     # z lemmatu: g_j = b_j XOR b_{j+1}
        print(f"{g:0{n}b}")  # n-bitový řetězec

Řešení podle Mata

Mat nechodí na přednášky a tak se rozhodl pro rekurzivní řešení

Zdroj obrázku: https://patamat.cz/

Využití pro účely výuky na ČVUT FEL dle AutZ §31a

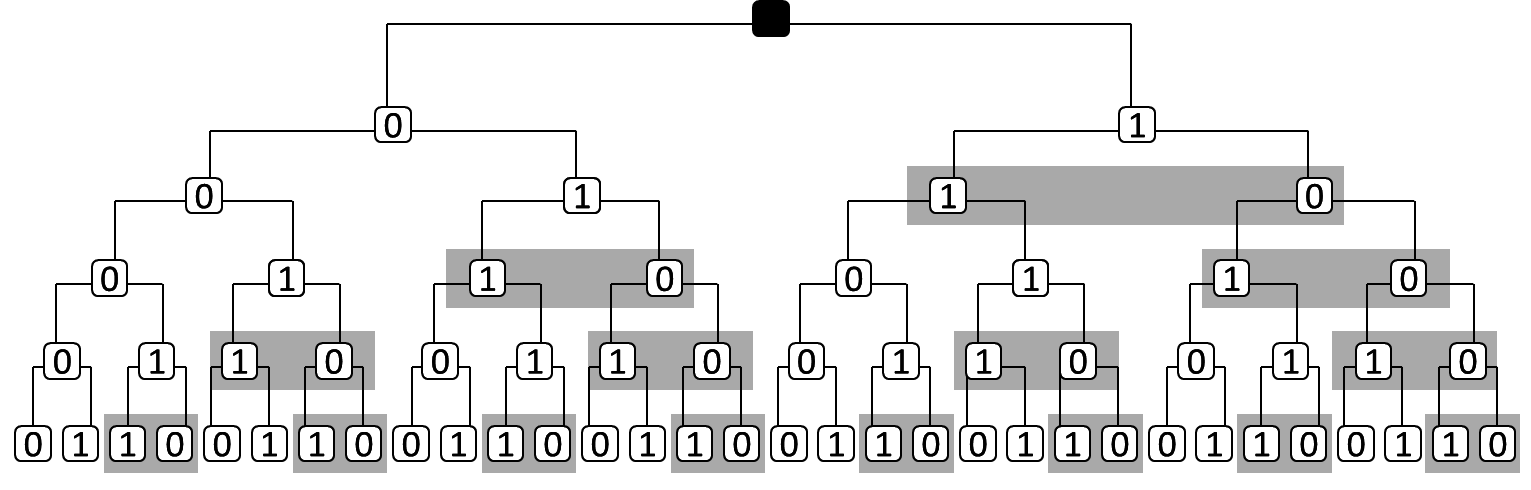
Všimněte si, že levé děti jsou $(0, 1)$ a pravé děti jsou $(1, 0)$ (obrácené pořadí)

Řešení podle Mata

Zdroj obrázku: https://patamat.cz/

Využití pro účely výuky na ČVUT FEL dle AutZ §31a

def gray(n: int) -> None:
    code = [0] * n

    def rec(k: int, firstcall: bool) -> None:
        if k == 0:
            # tisk od MSB k LSB (reverzně)
            print(''.join(str(code[i]) for i in range(n - 1, -1, -1)))
            return
        i = k - 1
        if firstcall:
            code[i] = 0; rec(k - 1, True)
            code[i] = 1; rec(k - 1, False)
        else:
            code[i] = 1; rec(k - 1, True)
            code[i] = 0; rec(k - 1, False)

    rec(n, True)

Příklad

Pointer problem

Všechny permutace množiny $M$ s $98$ prvky očíslujeme pořadovými čísly od $0$ do $98!−1$.

V programu pak nepracujeme s permutacemi ale jen s jejich pořadovými čísly. Víme, že budeme zkoumat pokaždé najednou $100$ permutací, čili v paměti budeme muset mít uloženo právě $100$ pořadových čísel různých permutací množiny $M$.

Kolik minimálně bitů si musíme v paměti rezervovat, abychom si těchto $100$ reprezentací mohli uložit?

Řešení

Každý "pořadový index" je číslo v rozsahu $0 ... 98!-1$

Minimální počet bitů na jedno číslo je $[\log_2(98!)]$

Výpočet:

$[\log_2(98!)] = 512$ bitů na jedno číslo
Pro 100 čísel: $100 \times 512 = 51\,200$ bitů

To odpovídá $6\,400$ bajtů

Příklad

Perm.NEXT()

Uvažujme všechny k-prvkové podmožiny množiny

$$M = \lbrace 1, 2, 3, ..., n \rbrace, 1 \leq k \leq n$$

Vyjděte z algoritmu transformujícího seznam prvků jedné podmnožiny na seznam prvků podmožiny bezprostředně následující v lexikografickém uspořádání těchto podmnožin.

Navrhněte a popište algoritmus, který bude transformovat seznam prvků jedné podmnožiny na seznam prvků podmožiny bezprostředně předcházející v témže lexokografickém uspořádání.

Bude mít stejnou asymptotickou složitost?

Řešení

Mějme kombinaci $(a_1 < a_2 < ... < a_k)$ z $\lbrace 1, ..., n \rbrace$ v lexikografickém pořadí.

NEXT

Najdi zprava první pozici, kterou lze zvětšit

def next_comb(a: List[int], n: int) -> Optional[List[int]]:
    k = len(a)
    b = a[:]  # kopie vstupu

    # hledej zprava první pozici, kterou lze zvětšit
    i = k - 1
    while i >= 0 and b[i] == n - (k - 1 - i):   # max na této pozici
        i -= 1
    if i < 0:
        return None  # a je poslední kombinace

    # zvětši ji a ocas nastav na nejmenší možné hodnoty
    b[i] += 1
    for j in range(i + 1, k):
        b[j] = b[j - 1] + 1
    return b

NEXT

Najdi zprava první pozici, kterou lze zvětšit

def next_comb(a: List[int], n: int) -> Optional[List[int]]:
    k = len(a)
    b = a[:]  # kopie vstupu

    # hledej zprava první pozici, kterou lze zvětšit
    i = k - 1
    while i >= 0 and b[i] == n - (k - 1 - i):   # max na této pozici
        i -= 1
    if i < 0:
        return None  # a je poslední kombinace

    # zvětši ji a ocas nastav na nejmenší možné hodnoty
    b[i] += 1
    for j in range(i + 1, k):
        b[j] = b[j - 1] + 1
    return b

PREV

Najdi zprava první pozici, kterou lze zmenšit bez porušení růstu prefixu

def prev_comb(a: List[int], n: int) -> Optional[List[int]]:
    k = len(a)
    b = a[:]

    # hledej zprava první pozici, kterou lze zmenšit
    i = k - 1
    while i >= 0 and b[i] == (1 if i == 0 else b[i - 1] + 1):  # minimum na pozici
        i -= 1
    if i < 0:
        return None  # a je úplně první kombinace (1,2,...,k)

    # zmenši ji a ocas nastav na největší možné hodnoty (co nejvíc vpravo)
    b[i] -= 1
    for j in range(i + 1, k):
        b[j] = n - (k - 1 - j)   # ... n-2, n-1, n
    return b

DEMO

# {1..8}, k=4
A = [2, 4, 6, 7]
print(next_comb(A, 8))  # -> [2, 4, 6, 8]
print(prev_comb(A, 8))  # -> [2, 4, 5, 8]

Jaká je tedy asymptotická složitost? Liší se u NEXT a PREV?

$$O(k)$$

Příklad

Bicykl

Uvažujeme permutace množiny $M = \lbrace 1, 2, 3, ..., n \rbrace$.

Cyklus délky $k$ v permutaci $p$ definujeme jako množinu
$$A = \lbrace a_1, a_2, ..., a_k \rbrace \subseteq M$$

pro kterou platí:
$$1 \leq a_1 < a_2 < ... < a_k \leq n$$

$$\begin{align*}p(a_j) &= a_{j+1} \text{ pro } 1 \leq j < k\\ p(a_k) &= a_1 \end{align*}$$
Určete, kolik je takových permutací množiny $\lbrace 1, 2, 3, ..., n \rbrace$, které obsahují právě dva cykly, z nichž jeden má délku $4$ a druhý délku $n-4$.

Řešení

Počet permutací na $\lbrace 1, ..., n \rbrace$, které mají přesně dva cykly délky $4$ a $n-4$:

Vyber 4 prvky do čtyřcyklu $\rightarrow \binom n 4$ možností
Počet možných "otočení" cyklu je $(4-1)! = 3! = 6$
Zbylých $n-4$ prvků tvoří 2. cyklus $\rightarrow$ $(n-4-1)!$ otočení

Celkem:

$$ \binom n 4 \cdot 6 \cdot (n-5)! $$

Příklad

TODO

Rank permutace $\pi$ množiny $N = \lbrace 0, 1, 2, ..., n─1 \rbrace$ je pořadové číslo této permutace v seznamu všech permutací množiny $N$ uspořádaném v rostoucím lexikografickém pořadí. Prvky seznamu jsou číslovány od $0$.

Napište pseudokód funkce která v čase úměrném $n$ vytiskne takovou permutaci $\pi$ množiny $N$, jejíž rank je právě $\frac{n!}{2}$.
Předpokládáme $n \geq 2$.

Příklad

TODO

Napište pseudokód funkce která v čase úměrném $n$ vytiskne takovou permutaci $\pi$ množiny $N$, jejíž rank je právě $\frac{n!}{2}$.
Předpokládáme $n \geq 2$.

Příklad

TODO

Uvažujme všechny permutace množiny $M = \lbrace 1, 2, 3, ..., n\rbrace$.

Vyjděte z algoritmu transformujícího danou permutaci na permutaci bezprostředně následující v lexikografickém uspořádání.

Navrhněte a popište algoritmus, který bude transformovat danou permutaci na permutaci bezprostředně předcházející v témže lexokografickém uspořádání. Bude mít stejnou asymptotickou složitost?

Příklad

TODO

Permutace $p$ množiny $\lbrace 1, 2, 3, ..., n \rbrace$ se nazývá derangement, pokud platí:

$$1 \leq k \leq n \Rightarrow p(k) \neq k$$

Napište všechny derangementy množiny $\lbrace 1, 2, 3, 4 \rbrace$.
Určete 1000000-tý prvek v lexikografickém uspořádání derangementů množiny $\lbrace 1, 2, 3, ..., 20\rbrace$.

Příklad

TODO

$P = (000, 001, 011, 110, 111, 101, 100)$ představuje Gray code $G_3$.

Dvě konečné posloupnosti $A$ a $B$ prohlásíme za ekvivalentní, pokud:

Obrácením pořadí prvků v $A$ získáme posloupnost $B$ nebo
Rotací o 1 nebo více pozic doleva nebo doprava posloupnosti $A$ získáme posloupnost $B$ nebo
Existuje posloupnost $C$ ekvivalentní s $A$ i s $B$.

Najděte 8-prvkovou posloupnost $Q$ představující Gray code, která není ekvivalentní s $P$.

⚠️ Gray code = binární soustava, kde se sousední prvky liší právě 1 bitem.

kombinatorika, Grayovy kódy

Příklad

Rank Permutace

Příklad

Permutace z Ranku

Příklad

Rank podmnožin

Příklad

Podmnožina z ranku

Příklad

Generátor zcela náhodných slov (bez opakování)

Příklad

Rekurze 101

Příklad

Přívětivé permutace

Příklad

Generování kódu pana šedého :)

Příklad

Pointer problem

Příklad

Perm.NEXT()

Příklad

Bicykl

Příklad

TODO

Příklad

TODO

Příklad

TODO

Příklad

TODO

Příklad

TODO

Na Viděnou Za týden :)

Na
Viděnou
Za týden :)