Konečné automaty, Regulární výrazy
LAB 08
B4M33PAL - Ing. David Pařil
Příklad
Par de expresiones regulares
Nad abecedou \(\lbrace 0, 1 \rbrace\), jsou dány dva jazyky \(L_1\) a \(L_2\). Slova \(L_1\) jsou popsána regulárním výrazem 0*1*0*1*0*, slova \(L_2\) jsou popsána regulárním výrazem (01+10)*.
-
Najděte nejkratší neprázdné slovo v průniku \(L_1 \cap L_2\).
-
Najděte nejdelší slovo v průniku \(L_1 \cap L_2\).
-
Najděte nejkratší slovo, které leží v \(L_1\), ale neleží v \(L_2\).
-
Najděte nejkratší slovo, které leží v \(L_2\), ale neleží v \(L_1\).
-
Najděte nejkratší slovo, které neleží v \(L_1 \cup L_2\).
\[\begin{array}{|l|l|l|}\hline \text{\textbf{Symbol}}&\text{\textbf{Význam}}&\text{\textbf{Příklad}}\\\hline R+S\;(\text{nebo }R\cup S)&\text{sjednocení / alternace}&0+1\ \text{ přijme }0\text{ nebo }1\\ R^{*}&0\times \text{ a více}&(01)^{*}=\varepsilon,\,01,\,0101,\ldots\\ (R)&\text{závorky}&0(10+01)\\ R?&0\times \text{ nebo }1\times=R+\varepsilon&0?=\varepsilon \text{ nebo }0\\ R^{+}&1\times \text{ a více }=RR^{*}&(01)^{+}\\\hline\end{array}\]
Nad abecedou \(\lbrace 0, 1 \rbrace\), jsou dány dva jazyky \(L_1\) a \(L_2\). Slova \(L_1\) jsou popsána regulárním výrazem 0*1*0*1*0*, slova \(L_2\) jsou popsána regulárním výrazem (01+10)*.
-
Najděte nejkratší neprázdné slovo v průniku \(L_1 \cap L_2\).
-
Najděte nejdelší slovo v průniku \(L_1 \cap L_2\).
-
Najděte nejkratší slovo, které leží v \(L_1\), ale neleží v \(L_2\).
-
Najděte nejkratší slovo, které leží v \(L_2\), ale neleží v \(L_1\).
-
Najděte nejkratší slovo, které neleží v \(L_1 \cup L_2\).
Řešení
Co přesně generují výrazy:
0*1*0*1*0*
(01+10)*
000…
111…
000…
111…
000…
01
10
0*1*0*1*0*
(01+10)*
000…
111…
000…
111…
000…
01
10
1) Najděte nejkratší neprázdné slovo v průniku \(L_1 \cap L_2\).
01
0
1
nebo
10
1
0
0*1*0*1*0*
(01+10)*
000…
111…
000…
111…
000…
01
10
2) Najděte nejdelší slovo v průniku \(L_1 \cap L_2\).
01
10
01
10
0
11
00
11
0
0*1*0*1*0*
(01+10)*
000…
111…
000…
111…
000…
01
10
3) Najděte nejkratší slovo, které leží v \(L_1\), ale neleží v \(L_2\).
01
0
nebo
10
1
0*1*0*1*0*
(01+10)*
000…
111…
000…
111…
000…
01
10
4) Najděte nejkratší slovo, které leží v \(L_2\), ale neleží v \(L_1\).
01
0
nebo
10
1
1
01
01
0
1
0
10
10
0
1
0
0*1*0*1*0*
(01+10)*
000…
111…
000…
111…
000…
01
10
5) Najděte nejkratší slovo, které neleží v \(L_1 \cup L_2\).
10
1
10
10
0
1
0
1
0
1
0
1
\(L_1\) Pokrývá všechna slova délky \(\leq 4\)
Příklad
Stavové Diagramy
Nakreslete stavový diagram automatu přijímajícího právě všechna slova nad abecedou \(\lbrace0,1\rbrace\), která:
-
obsahují podposloupnost
1010alespoň jednou -
neobsahují podposloupnost
1010 -
obsahují podposloupnost
1010právě jednou -
obsahují podposloupnost
1010nejvýše dvakrát
Řešení
1) Obsahují podposloupnost 1010 alespoň jednou
NFA:
DFA:
B
S
A
C
D
0,1
1
0
1
0
0,1
B
S
A
C
D
0
1
0
1
0
0,1
1
0
1
Řešení
2) Neobsahují podposloupnost 1010
DFA:
1
B
S
A
C
D
0
1
0
1
0
0,1
0
1
Pouhé prohození akceptačních stavů
Řešení
3) Obsahují podposloupnost 1010 právě jednou
DFA:
1
B
S
A
C
D
0
1
0
1
0
0
1
1
B'
S'
A'
C'
D'
0
1
0
1
0
0
1
0,1
0
E
F
0
0,1
1
1
0,1
Řešení
4) Obsahují podposloupnost 1010 nejvýše dvakrát
DFA:
0
1
S
A
B
C
1
0
1
0
1
0
D
0
1
B'
A'
C'
1
0
1
0
1
D'
0
1
B''
A''
C''
D''
1
0
1
0
0
1
0
0
První výskyt \(\rightarrow\)
Druhý výskyt \(\rightarrow\)
Třetí výskyt \(\rightarrow\)
Příklad
Návrh regulárních jazyků
Napište regulární výraz pro jazyk nad abecedou \(\lbrace 0, 1 \rbrace \)
- jehož slova obsahují pouze nuly
- jehož každé slovo obsahuje právě jedinou jedničku
- jehož každé slovo obsahuje alespoň jednu jedničku
- jehož každé slovo obsahuje alespoň dvě jedničky
- jehož slova obsahují sudý počet jedniček
- jehož slova obsahují lichý počet jedniček
Napište regulární výraz pro jazyk nad abecedou \(\lbrace 0, 1 \rbrace \)
- jehož slova obsahují pouze nuly
-
00*
-
- jehož každé slovo obsahuje právě jedinou jedničku
-
0*10*
-
- jehož každé slovo obsahuje alespoň jednu jedničku
-
0*1(0+1)*nebo(0+1)*10*nebo(0+1)*1(0+1)*
-
- jehož každé slovo obsahuje alespoň dvě jedničky
-
0*10*1(0+1)*nebo(0+1)*10*10*
-
- jehož slova obsahují sudý počet jedniček
-
(0*10*1)*0*nebo0*(10*10*)*
-
- jehož slova obsahují lichý počet jedniček
-
(0*10*1)*0*10*nebo0*10*(10*10*)*
-
Příklad
Počítáme s automaty
Navrhněte NKA (nedeterministický konečný automat) nad abecedou \(\lbrace0, 1, 2\rbrace\), který v textu vyhledá všechny řetězce obsahující tři nuly, dvě jedničky a žádné dvojky
Navrhněte NKA (nedeterministický konečný automat) nad abecedou \(\lbrace0, 1, 2\rbrace\), který v textu vyhledá všechny řetězce obsahující tři nuly a dvě jedničky
Řešení
B
S
A
C
0,1,2
0
0
0
F
D
E
G
0
0
0
1
1
1
1
J
H
I
K
0
0
0
1
1
1
1
Jak najít všechny
řetězce (ne jen první)?
Řešení
B
S
A
C
0,1
0
0
0
F
D
E
G
0
0
0
1
1
1
1
J
H
I
K
0
0
0
1
1
1
1
Všimněte si absence jakékoli sebe-smyčky ve stavu \(K\).
Někteří studenti často nechápou, že automat je vyhledávací automat, takže když je v konečném stavu, pouze hlásí, že nalezl podřetězec.
Konkrétní větev výpočtu (pamatujte, že se jedná o NFA provádějící mnoho větví výpočtu) poté končí.
Příklad
#Automat #NKA #abababa
Navrhněte NKA nad abecedou \(\lbrace a, b, c, d \rbrace \), který v textu vyhledá všechny řetězce ve tvaru #ba##b#, kde symbol # představuje právě jeden libovolný znak z množiny \(\lbrace a, b, d \rbrace \).
Automat musí být schopen zpracovat celý text libovolné délky, tj. octnout se v koncovém stavu po přečtení posledního znaku každého výskytu hledaného řetězce.
Řešení
Navrhněte NKA nad abecedou \(\lbrace a, b, c, d \rbrace \), který v textu vyhledá všechny řetězce ve tvaru #ba##b#, kde symbol # představuje právě jeden libovolný znak z množiny \(\lbrace a, b, d \rbrace \).
Automat musí být schopen zpracovat celý text libovolné délky, tj. octnout se v koncovém stavu po přečtení posledního znaku každého výskytu hledaného řetězce.
S
B
a,b,c,d
a,b,d
A
C
D
F
E
G
b
a
a,b,d
a,b,d
b
a,b,d
Příklad
Žábomat
Sestavte automat, který v textu nad abecedou \(A\) vyhledává všechna slova popsaná regulárním výrazem \(R\).
\(A = \lbrace a,b,c \rbrace\), \(R =\) (ac* + bb)*a
Sestavte automat, který v textu nad abecedou \(A\) vyhledává všechna slova popsaná regulárním výrazem \(R\).
\(A = \lbrace a,b,c \rbrace\), \(R =\) (ac* + bb)*a
Řešení
ac
bb
accc
acc
bb
bb
a
a
Sestavte automat, který v textu nad abecedou \(A\) vyhledává všechna slova popsaná regulárním výrazem \(R\).
\(A = \lbrace a,b,c \rbrace\), \(R =\) (ac* + bb)*a
S
a
ac
bb
accc
acc
bb
bb
a
a
c
b
b
a

c
a
b
a
b
b
a
a
b
b
a
a
c
a
Příklad
Převrácená želva-o-mat
Mějme abecedu \(A= \lbrace a, b, c, ..., z \rbrace \).
Pořadové číslo znaku a bude 1,
pořadové číslo znaku b bude 2, atd, až
pořadové číslo znaku z bude 26.
Slovo nad \(A\) nazveme uspořádané, pokud pro každý jeho znak platí, že všechny znaky za ním ve slově následující mají vyšší pořadové číslo než tento znak.
Sestavte NKA, který vyhledá v textu nad abecedou \(A\) všechna uspořádaná slova.
Řešení
S
A
B
C
D
E
F
G
Zkrácená verze pro \(A= \lbrace a, b, c, d, e, f, g \rbrace \).
a,b,c,d,e,f
Z definice každý substring délky 1 je taktéž uspořádané slovo.
Tedy (mimo jiné) každý znak bude detekován jako uspořádané slovo...

Příklad
Porovnávání počtu s pomocí automatů
Sestavte NKA nad abecedou \(\lbrace 0, 1, 2 \rbrace\), který v textu vyhledá všechny řetězce obsahující stejný počet znaků \(0\), \(1\) i \(2\).
Řešení
Takový konečný automat neexistuje!!
Pro porovnání počtu nul a jedniček v jakémkoli možném slově by potřeboval nekonečně mnoho stavů, z nichž každý by registroval určitý počet (nepárovaných jedničkami) dosud přečtených nul.
Jeho neexistence je důsledkem základní věty zvané pumpovací lemma pro regulární jazyky.
Ačkoli lemma v kurzu Algoritmy neuvádíme/nepřipomínáme, očekáváme, že lepší studenti kurzu budou obeznámeni s myšlenkou, že jakýkoli jazyk, jehož rozpoznávání vyžaduje počítání neomezeného počtu výskytů nějakých symbolů/podřetězců, není regulární.
Typickým příkladem takové nemožnosti je jazyk všech správně tvarovaných závorkových výrazů nebo jen párování závorek.
https://en.wikipedia.org/wiki/Context-free_grammar#Well-formed_parentheses
https://en.wikipedia.org/wiki/Context-free_grammar#Matching_pairs
Příklad
Ověření certifikátu
Chtěli bychom sestavit konečný automat nad abecedou \(\lbrace0, 1\rbrace\), který přijímá všechna slova, která představují certifikát nějakého neorientovaného stromu.
Vysvětlete, zda to je či není možné, a pokud to možné je, popište, jak by se takový automat konstruoval.
Řešení
Protože každý certifikát představuje řetězec správně tvarovaných závorek (0 a 1 odpovídají otevírací a uzavírací závorce), platí pro tento problém stejný "postup" jako v předchozím problému. Příklad nemá řešení!
Příklad
Operace ROT
Operace ROT zvolí některý znak \(x\) v řetězci a nahradí ho znakem v abecedě bezprostředně následujícím za \(x\).
Pokud \(x\) je poslední znak v abecedě, nahradí ho znakem prvním v abecedě.
Sestavte NKA, který v textu vyhledá všechny podřetězce, které lze z daného vzorku aabcb získat pomocí nejvýše dvou operací ROT.
Abeceda je \(\lbrace a, b, c\rbrace\).
Řešení
S
A
B
C
D
E
A'
B'
C'
D'
E'
B''
C''
D''
E''
a
a
b
c
b
b
b
c
a
c
a
b
c
b
b
c
b
b
c
a
c
a,b,c
Příklad
Podobnost regulárních výrazů
Rozhodněte, zda uvedené regulární výrazy představují stejný regulární jazyk.
(01+0)*00(10+0)*
Rozhodněte, zda uvedené regulární výrazy představují stejný regulární jazyk.
(01+0)*00(10+0)*
Řešení
Ano!
Oba obsahují všechny konečné řetězce sestávající pouze z nul.
Každý řetězec v obou jazycích začíná nulou a končí nulou.
Jakýkoli řetězec, který neobsahuje podřetězec 11, je v obou jazycích slovo.
Příklad
TODO
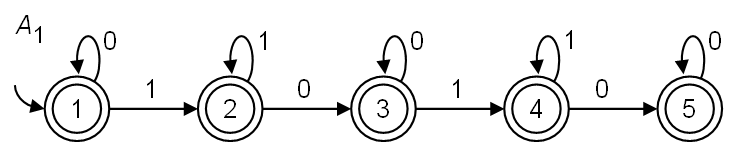
Popište neformálně, jaký jazyk přijímá uvedený automat nad
abecedou \(\lbrace0, 1\rbrace\).
Napište regulární výraz popisující týž jazyk.
Příklad
TODO
Napište regulární výraz popisující maximální (vzhledem k inkluzi) množinu M řetězců nad abecedou {a, b, c} takovou, že:
a) každý řetězec v M začíná i končí symbolem b,
b) každý řetězec v M obsahuje právě jediný výskyt symbolu c kdekoli v řetězci,
c) žádný řetězec v M nesmí na liché pozici obsahovat symbol a (pozice se číslují od 1).