Číselně teoretické algoritmy
LAB 10
B4M33PAL - Ing. David Pařil
Příklad
perfektně rozsypaný hrášek
Máme dva obrázky - pokaždé jde o čtverec se 100 body uvnitř.
- obrázek - souřadnice každého bodu generovány nezávisle a pseudonáhodně
- obrázek - souřadnice byly generovány analogicky, ale navíc byly souřadnice systematicky modifikovány (nám neznámým) způsobem.
Odhadněte, kterého obrázku se týkají dodatečné úpravy a zdůvodněte svůj odhad.

- obrázek - souřadnice každého bodu generovány nezávisle a pseudonáhodně
- obrázek - souřadnice byly generovány analogicky, ale navíc byly souřadnice systematicky modifikovány (nám neznámým) způsobem.
- obrázek - souřadnice každého bodu generovány nezávisle a pseudonáhodně
- obrázek - souřadnice byly generovány analogicky, ale navíc byly souřadnice systematicky modifikovány (nám neznámým) způsobem.
- obrázek - souřadnice každého bodu generovány nezávisle a pseudonáhodně
- obrázek - souřadnice byly generovány analogicky, ale navíc byly souřadnice systematicky modifikovány (nám neznámým) způsobem.
První obrázek je systematicky modifikován.
(Každá buňka z mřížky 10x10 obsahuje právě 1 bod \(\rightarrow\) body byly generovány per-buňka)
Druhý obrázek reprezentuje klasické náhodné generování přes celý canvas.
Příklad
Jedna rudá kostka, 11 možností
Máte jednu hrací kostku.
Popište, jak využijte házení kostkou tak, abyste měli generátor náhodných celých čísel v rozmezí 0...10.
Všechna čísla 0, 1, 2, …, 10 musí být generována se stejnou pstí.

Příklad řešení
- Hoďte hrací kostkou dvakrát
- Máte 12 možných výstupů (všechny stejně pravděpodobné)
- Rozhodněte:
- Prvních 11 výstupů namapujte na čísla 0, 1, ..., 10
- Pokud padne 12. výstup vraťte se do kroku 1.

Příklad
Náhodné pole
Vysvětlete, jak pomocí generátoru náhodných čísel zamícháte do náhodného pořadí seřazené pole čísel.
Akce musí proběhnout v čase úměrném délce pole.
1
2
3
4
5
6
7
8
9
0
Seřazené:
1
2
3
4
5
6
7
8
9
0
Postupně tvořím nové pole vybíráním prvků z pole původního.
Náhodné:
8
5
2
6
0
1
9
3
7
4
Řešení
Jak to zapsat v kódu tak, abychom neplýtvali pamětí/allocama?
Knuth shuffle algoritmus (též Fisher–Yates alg.):
Postupně vybíráme náhodné prvky z dosud „nezamíchané“ části pole a prohazujete je na konec „zamíchané“ části.
Řešení
for i := n-1 downto 1 do
j := random(0, i) // celé číslo mezi 0 a i včetně
swap(A[i], A[j])-
Pro \(i\) od \(n-1\) dolů po \(1\):
-
vygenerujte náhodné celé číslo \(j\) z intervalu \(0 … i\)
-
prohoďte \(A[i]\) a \(A[j]\)
-
Po skončení cyklu je pole náhodně promíchané (rovnoměrné rozdělení).
Příklad
Lineární kongruentní generátory
Ověřte, zda lineární kongruentní generátor s danými parametry má maximální možnou délku periody.
- \(x_{n+1} = (91 x_n + 49) \bmod 600\)
- \(x_{n+1} = (\ \ 8 x_n + 80) \bmod \ \ 49\)
- \(x_{n+1} = (37 x_n + 55) \bmod 144\)
- \(x_{n+1} = (99 x_n + 81) \bmod 113\)

Řešení
Lineární kongruentní generátor:
$$x_{n+1} = (A x_n + C) \bmod M$$
má maximální periodu \(M\) iff:
- \(\text{GCD}(C, M) = 1\)
- pro každý prvočíselný dělitel \(p\) modulu \(M\) platí \(p|(A-1)\)
- jestliže \(4|M\), pak také \(4|(a-1)\)
\(p \text{ dělí }(A-1)\)
\(\text{nesoudělná}\)
aka Hull-Dobellovo kritérium
1) Řešení \(x_{n+1} = (91 x_n + 49) \bmod 600\)
Ověřujeme Hull-Dobellovo kritérium:
‣ \( M = 600 = 2^3 \cdot 3 \cdot 5^2 \)
- \(\text{GCD}(49, 600) = 1\) ✅
- \(p = \{2, 3, 5\}\); \(A-1 = 90\). Ověřujeme: \(2|90,\ 3|90,\ 5|90\) ✅
- \(4|600\) platí, ale \(4 \!\nmid\!90\) ❌
- Nemá maximální možnou periodu 🙁
2) Řešení \(x_{n+1} = (8 x_n + 80) \bmod 49\)
Ověřujeme Hull-Dobellovo kritérium:
‣ \( M = 49 = 7^2 \)
- \(\text{GCD}(80, 49) = 1\) ✅
- \(p = \{7\}\); \(A-1 = 7\). Ověřujeme: \(7|7\) ✅
- \(4 \!\nmid\! 49\) neplatí, není co řešit ✅
- Má maximální možnou periodu 😊
3) Řešení \(x_{n+1} = (37 x_n + 55) \bmod 144\)
Ověřujeme Hull-Dobellovo kritérium:
‣ \( M = 144 = 16 \cdot 9 = 2^4 \cdot 3^2 \)
- \(\text{GCD}(55, 144) = 1\) ✅
- \(p = \{2, 3\}\); \(A-1 = 36\). Ověřujeme: \(2|36,\ 3|36\) ✅
- \(4 | 144\) platí a zároveň \(4|36\) ✅
- Má maximální možnou periodu 😊
4) Řešení \(x_{n+1} = (99 x_n + 81) \bmod 113\)
Ověřujeme Hull-Dobellovo kritérium:
‣ \( M = 113 = \text{prvočíslo} \) 😯
- \(\text{GCD}(81, 113) = 1\) ✅
- \(p = \{113\}\); \(A-1 = 98\). Ověřujeme: \(113|89\) ❌
- Už není co řešit
- Nemá maximální možnou periodu 😭
Příklad
Lehmerův generátor
Určete délku periody v Lehmerově generátoru, který je dán předpisem
$$x_{n+1} = ((M-1)\cdot x_n) \bmod M$$
kde \(M\) je prvočíslo.

Pozn: Obecný Lehmer:
$$x_{n+1} = (A \cdot x_n) \bmod M$$
Řešení
Máme:
$$x_{n+1} = ((M-1)\cdot x_n) \bmod M$$
Protože \(M - 1 \equiv -1 \) (\(\bmod M\)), můžeme psát:
$$x_{n+1} = ((M-1)\cdot x_n) \bmod M = (M \cdot x_n - x_n) \bmod M \equiv -x_n \bmod M$$
Z toho vyplývá, že se nám bude v cyklu negovat vstupní \(x_0\):
$$[x_0, -x_0, x_0, -x_0, ...] \bmod M$$
Tedy perioda tohoto generátoru je 2.
Příklad
Myslím, že jich bude alespoň pět
Určete, kolik přibližně prvočísel leží v intervalu:
- \([0, 10^9]\)
- \([10^9, 2 \cdot 10^9]\)
- \([2\cdot 10^9, 3\cdot 10^9]\)
\(0\)
\(10^9\)
\(2\cdot 10^9\)
\(3\cdot 10^9\)
1. ???
2. ???
3. ???
Řešení
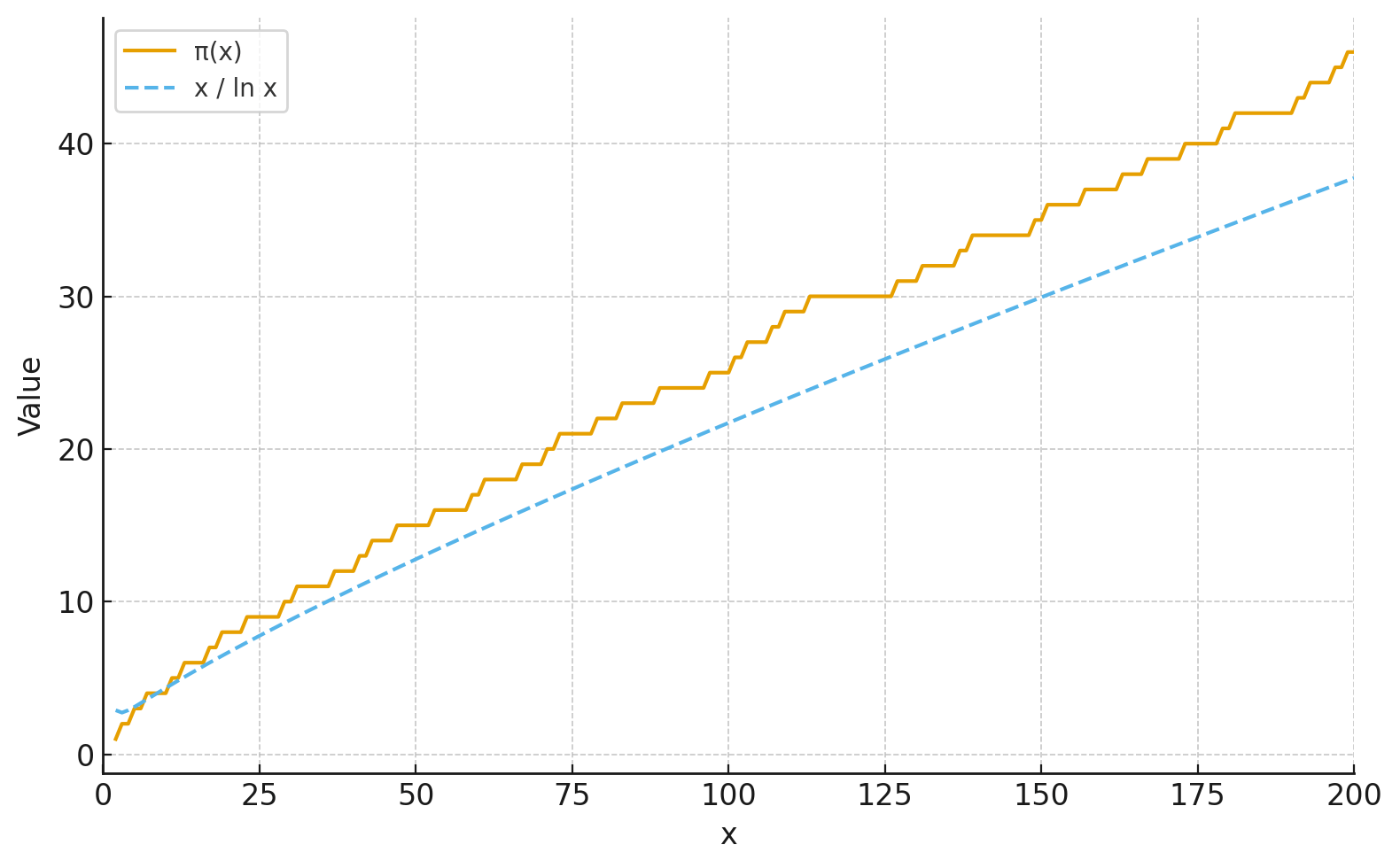
Použijeme větu o rozdělení prvočísel:
$$\pi(x) \approx \frac{x}{\ln x}$$
kde \(\pi(x)\) je počet prvočísel \(\leq x\)
- \(\pi(10^9) \approx \frac{10^9}{\ln(10^9)} = \frac{10^9}{9\ln(10)}\approx 48\,000\,000\)
- \(\pi(2 \cdot 10^9) - \pi(10^9) \approx \frac{2\cdot 10^9}{\ln(2\cdot 10^9)} - \frac{10^9}{\ln(10^9)} \approx 45\,000\,000\)
- \(\pi(3 \cdot 10^9) - \pi(2 \cdot 10^9) \approx \frac{3\cdot 10^9}{\ln(3\cdot 10^9)} - \frac{2\cdot 10^9}{\ln(2\cdot 10^9)} \approx 44\,000\,000\)
\(0\)
\(10^9\)
\(2\cdot 10^9\)
\(3\cdot 10^9\)
1. ???
2. ???
3. ???
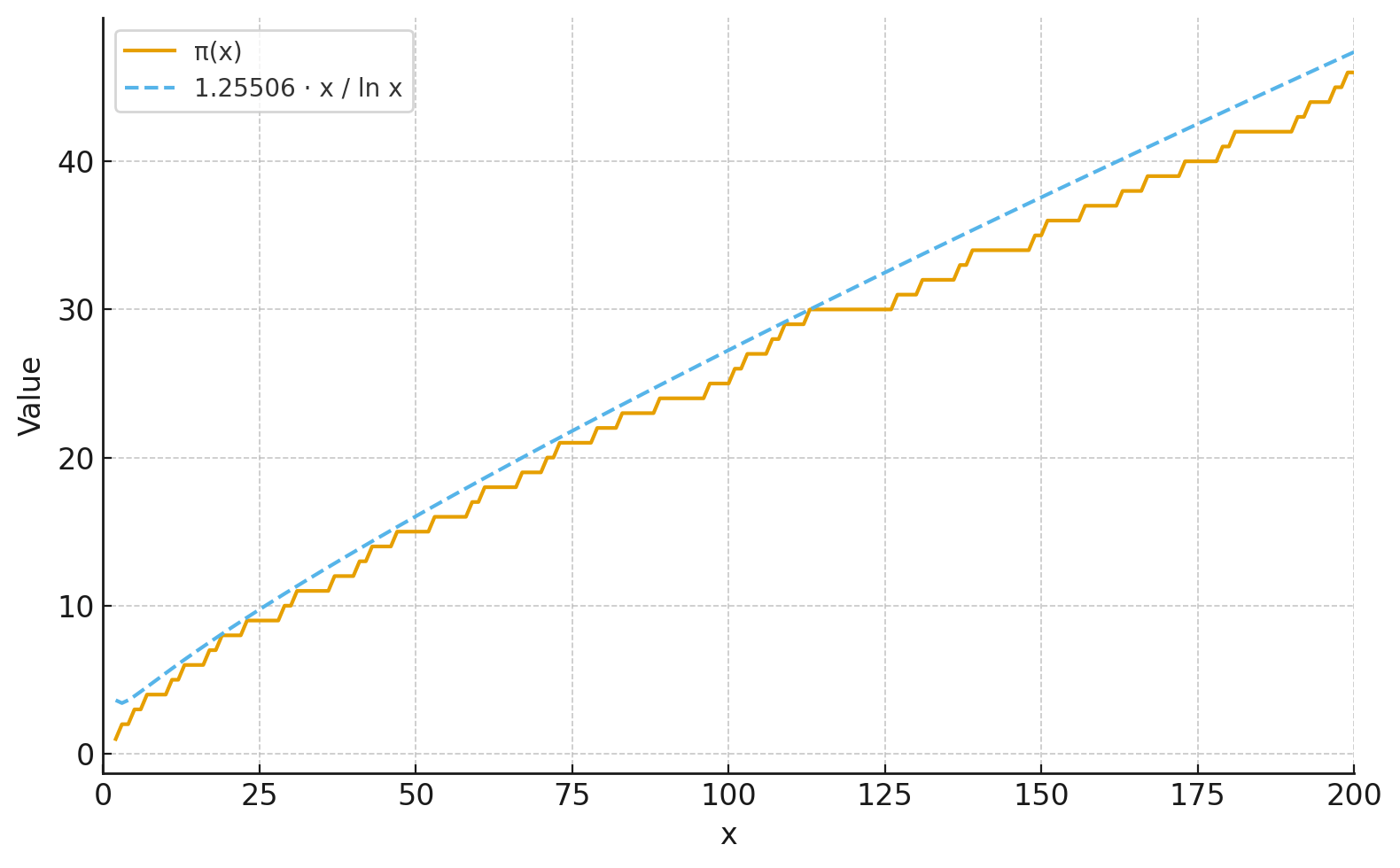
Platí:
$$\pi(x) < 1.25506 \frac x {\ln(x)}$$
Příklad
polo-Eratosthenovo síto
Řekneme, že přirozené číslo je poloprvočíslo, pokud je buď prvočíslem nebo celou mocninou prvočísla.
Popište modifikaci Eratosthenova síta, která bude generovat právě poloprvočísla. Napište pseudokód.

Eratosthenovo síto


~200 let př. n. l.:
- změřil poloměr země
- vynalezl Erato. síto
- má kráter na měsíci
Zdroj: https://cs.wikipedia.org/wiki/Eratosthenovo_s%C3%ADto
Řešení
Popište modifikaci Eratosthenova síta, která bude generovat právě poloprvočísla. Napište pseudokód.
procedure semiprimes(N):
// 1) klasické síto – najdeme prvočísla
for i := 2 to N do
is_prime[i] := true
for i := 2 while i * i <= N do
if is_prime[i] then
j := i * i
while j <= N do
is_prime[j] := false
j := j + i
// 2) z prvočísel vyrobíme poloprvočísla (p, p^2, p^3, ...)
for i := 2 to N do
is_semiprime[i] := false
for p := 2 to N do
if is_prime[p] then // p je prvočíslo
x := p
while x <= N do
is_semiprime[x] := true
x := x * p // další mocnina p^kJde to i lépe
procedure semiprimes(N):
for i := 2 to N do
cnt[i] := 0
for i := 2 to N do
if cnt[i] = 0 then // i je prvočíslo
j := i
while j <= N do
cnt[j] := cnt[j] + 1 // i je jedním z prvočíselných dělitelů j
j := j + i
// výpis poloprvočísel (prvočísla + jejich mocniny)
for n := 2 to N do
if cnt[n] = 1 then
output n
procedure semiprimes(N):
// 1) klasické síto – najdeme prvočísla
for i := 2 to N do
is_prime[i] := true
for i := 2 while i * i <= N do
if is_prime[i] then
j := i * i
while j <= N do
is_prime[j] := false
j := j + i
// 2) z prvočísel vyrobíme poloprvočísla (p, p^2, p^3, ...)
for i := 2 to N do
is_semiprime[i] := false
for p := 2 to N do
if is_prime[p] then // p je prvočíslo
x := p
while x <= N do
is_semiprime[x] := true
x := x * p // další mocnina p^kJako skoroprvočísla označíme právě ta přirozená čísla, která jsou součinem dvou různých prvočísel.
Popište modifikaci Eratosthenova síta, která bude generovat skoroprvočísla. Napište pseudokód.
Příklad
Skoro-Eratosthenovo síto

Řešení
procedure almostprimes(N):
for i := 2 to N do
count[i] := 0
for p := 2 to N do
if is_prime[p] then
j := p
while j <= N do
count[j] := count[j] + 1
j := j + p
// skoroprvočísla:
for n := 2 to N do
if count[n] = 2 then
output nprocedure almostprimes(N):
for i := 2 to N do
count[i] := 0
for p := 2 to N do
if is_prime[p] then
j := p
while j <= N do
count[j] := count[j] + 1
j := j + p
// skoroprvočísla:
for n := 2 to N do
if count[n] = 2 then
output nPříklad
Princip síta
Vygenerujeme všech 168 prvočísel menších než 1000 (2, 3, 5, …, 991, 997) a dále ze seznamu S = (1000, 1001, …, 999999) všech celých čísel větších než 999 a menších než 1000000 vyškrtneme všechny násobky uvedených prvočísel.
Kolik čísel zbyde v S a kolik z nich budou prvočísla? Uveďte co nepřesnější odhad.

Řešení

Blokující prvočísla
Ostatní prvočísla
Každé složené číslo z intervalu \((10^3, 10^6)\) má nějaký prvočíselný dělitel z intervalu \((0, 10^3)\)
Po síťování zůstanou v \(S\) jen čísla, která vůbec nemají prvočíselný dělitel \(< 1000\), tedy právě prvočísla
$$\pi(999999) - \pi(999)$$
$$=78498-168$$
$$=78330$$
(přibližně)
Zdroj: https://cs.wikipedia.org/wiki/Eratosthenovo_s%C3%ADto
Příklad
Počet prvočísel
Určete, jaký je maximální možný počet prvočísel v kterémkoli z intervalů:
$$[30k, 30k+29], \quad k = 1, 2, 3, 4, ...$$
Řešení
1
2
3
4
5
6
7
8
9
0
11
12
13
14
15
16
17
18
19
10
21
22
23
24
25
26
27
28
29
20
31
32
33
34
35
36
37
38
39
30
41
42
43
44
45
46
47
48
49
40
51
52
53
54
55
56
57
58
59
50
61
62
63
64
65
66
67
68
69
60
71
72
73
74
75
76
77
78
79
70
81
82
83
84
85
86
87
88
89
80
91
92
93
94
95
96
97
98
99
90
99
101
102
103
104
105
106
107
108
109
100
111
112
113
114
115
116
117
118
119
110
0-29
10 prvočísel
30-59
7 prvočísel
17 celkem
60-89
7 prvočísel
24 celkem
90-119
6 prvočísel
30 celkem
Rozsah: \([30k, 30k+29]\)
Platí:
$$\pi(x) < 1.25506 \frac x {\ln(x)}$$
\(\pi(30) < 11.07\)
\(\pi(60) < 18.39\)
\(\pi(90) < 25.10\)
\(\pi(120) < 31.45\)
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
120-149
5 prvočísel
35 celkem
\(\pi(150) < 37.57\)
150-179
6 prvočísel
41 celkem
\(\pi(180) < 43.50\)
180-209
5 prvočísel
46 celkem
\(\pi(210) < 49.29\)
Řešení
1
2
3
4
5
6
7
8
9
0
11
12
13
14
15
16
17
18
19
10
21
22
23
24
25
26
27
28
29
20
31
32
33
34
35
36
37
38
39
30
41
42
43
44
45
46
47
48
49
40
51
52
53
54
55
56
57
58
59
50
61
62
63
64
65
66
67
68
69
60
71
72
73
74
75
76
77
78
79
70
81
82
83
84
85
86
87
88
89
80
91
92
93
94
95
96
97
98
99
90
99
101
102
103
104
105
106
107
108
109
100
111
112
113
114
115
116
117
118
119
110
0-29
10 prvočísel
30-59
7 prvočísel
17 celkem
60-89
7 prvočísel
24 celkem
90-119
6 prvočísel
30 celkem
Rozsah: \([30k, 30k+29]\)
Platí:
$$\pi(x) < 1.25506 \frac x {\ln(x)}$$
\(\pi(30) < 11.07\)
\(\pi(60) < 18.39\)
\(\pi(90) < 25.10\)
\(\pi(120) < 31.45\)
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
120-149
5 prvočísel
35 celkem
\(\pi(150) < 37.57\)
150-179
6 prvočísel
41 celkem
\(\pi(180) < 43.50\)
180-209
5 prvočísel
46 celkem
\(\pi(210) < 49.29\)
Příklad
TODO
Vypočtěte:
- \(\text{GCD}(220, 284)\)
- \(\text{GCD}\left( \binom{30}{10}, \binom{31}{9} \right)\)
- \(\text{GCD}(2100, 100!)\)