Generative vs discriminative probabilistic models

Discriminative classification

Given a training set \( \{\pmb{x}_n, \pmb{c}_n \}\) consisting of features \( \pmb{x}_n \) (predictors) and target vectors \( \pmb{c}_n \) solve:

Generative classification

p(\pmb{\theta}|\pmb{D}) \propto p(\pmb{\theta}) \prod_n p_{\pmb{\theta}}(c_n|\pmb{x}_n)

p(\pmb{\theta}|\pmb{D}) \propto p(\pmb{\theta}) \prod_n p_{\pmb{\theta}}(\pmb{x}_n|\pmb{c}_n) p(\pmb{c}_n)

can exploit unlabelled data in addition to labelled data.

requires potentially expensive data labeling.

better generalization performance.

Bernardo, J. M., et al. "Generative or discriminative? getting the best of both worlds." Bayesian statistics 8.3 (2007): 3-24.

Mackowiak, Radek, et al. "Generative classifiers as a basis for trustworthy image classification." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.

Wu, Ying Nian, et al. "A tale of three probabilistic families: Discriminative, descriptive, and generative models." Quarterly of Applied Mathematics 77.2 (2019): 423-465.

Ho, Nhat, et al. "Neural rendering model: Joint generation and prediction for semi-supervised learning." arXiv preprint arXiv:1811.02657 (2018).

Hsu, Anne, and Thomas Griffiths. "Effects of generative and discriminative learning on use of category variability." Proceedings of the Annual Meeting of the Cognitive Science Society. Vol. 32. No. 32. 2010.

Mixture models

p_{\pmb{\theta}}(\pmb{X}) = \prod_{n=1}^N p_{\pmb{\theta}}(\pmb{x}_n) = \prod_{n=1}^N \sum_{z_n} p_{\pmb{\theta}}(\pmb{x}_n|z_n)p_{\pmb{\theta}}(z_n)

\ln p(\pmb{X}) = \int \text{d} \pmb{\theta} q(\pmb{\theta}) \left[ \sum_{n=1}^N \sum_{z_n} q(z_n) \ln \frac{q(\pmb{z_n})}{p_{\pmb{\theta}}(\pmb{x}_n|z_n)p_{\pmb{\theta}}(z_n)} + \ln \frac{q(\pmb{\theta})}{p(\pmb{\theta})}\right]

Variational free energy

Exponential family

p_{\pmb{\theta}}(\pmb{x}_n|z_n) = h(\pmb{x}_n) \exp\left\{\pmb{\theta}_{z_n} \cdot \pmb{T}(\pmb{x}_n) - A_{z_n}\right\}

Mixture models

\begin{split} q_{k+1}(z_n) &\propto e^{\left < \ln p_{\pmb{\theta}_{z_n}}(\pmb{x}_n) \right>_{q_k(\pmb{\theta}_{z_n})} + \left< \ln p_{\pmb{\rho}}(z_n) \right>_{q_k(\pmb{\rho})} } \\ q_{k+1}(\pmb{\theta}_z) &\propto p(\pmb{\theta}_z)e^{\sum_n q_{k+1}(z_n=z)p_{\pmb{\theta}_z}(\pmb{x}_n)} \\ q_{k+1}(\pmb{\rho}) &\propto p(\pmb{\rho}) e^{\sum_n \sum_{z_n} q_{k+1}(z_n) \ln p_{\pmb{\rho}} (z_n)} \end{split}

Iterative updating

Mixture models

\begin{split} q(z_n) &\propto e^{\left < \ln p_{\pmb{\theta}_{z_n}}(\pmb{x}_n) \right>_{q(\pmb{\theta}_{z_n})} + \left< \ln p_{\pmb{\rho}}(z_n) \right>_{q(\pmb{\rho})} } \\ \end{split}

A link to multinomial regression

\pmb{T}(\pmb{x}) = \left( \pmb{x}, \pmb{f}_1(\pmb{x}), \pmb{f}_2 (\pmb{x}), \ldots \right) \\ \pmb{\theta}_z = \left(\pmb{\theta}^0_z, \pmb{\theta}^1, \pmb{\theta}^2, \ldots \right)

q(z_n = i) = \frac{e^{\bar{\pmb{\theta}}^0_{i} \pmb{x}_n + b_{i}} }{\sum_k e^{\bar{\pmb{\theta}}^0_k \pmb{x}_n + b_{k}}}

Classification with MM

c_n^* = \argmax_i \frac{e^{\bar{\pmb{\theta}}^0_{i} \pmb{x}_n^* + b_{i}} }{\sum_k e^{\bar{\pmb{\theta}}^0_k \pmb{x}_n^* + b_{k}}}

1. Given a training set \( \{\pmb{x}_n, c_n \}\) map labels \( c_n \) to one hot encoded vectors \( \pmb{e}[c_n] \)

2. Update parameters

\begin{split} q(\pmb{\theta}_c) &\propto p(\pmb{\theta}_c)e^{\sum_n e_c[c_n] p_{\pmb{\theta}_c}(\pmb{x}_n)} \\ q(\pmb{\rho}) &\propto p(\pmb{\rho}) e^{\sum_n \pmb{e}[c_n]^T \cdot \ln p_{\pmb{\rho}} (c_n)} \end{split}

3. Given a test set \( \{\pmb{x}^*_n \}\) predict labels as

Discriminative classification

c_n^* = \argmax_i \frac{e^{E_{q(\pmb{W}, \pmb{b})} \left[\ln p(i|\pmb{W} \cdot \pmb{x}_n^* + \pmb{b} ) \right]}}{\sum_k e^{E_{q(\pmb{W}, \pmb{b})} \left[\ln p(k|\pmb{W} \cdot \pmb{x}_n^* + \pmb{b} ) \right]}}

1. Given a training set \( \{\pmb{x}_n, c_n \}\) learn model parameters using (approximate) inference

\begin{split} p(\pmb{W}, \pmb{b}|\pmb{\mathcal{D}}) \propto p(\pmb{W}) p(\pmb{b}) \prod_{n=1}^N p(c_n| \pmb{W} \cdot \pmb{x}_n + \pmb{b}) \end{split}

2. Given a test set \( \{\pmb{x}^*_n \}\) predict labels as

Wojnowicz, Michael T., et al. "Easy Variational Inference for Categorical Models via an Independent Binary Approximation." International Conference on Machine Learning. PMLR, 2022.

Semi-supervised learning

1. Given fully labeled \( \{\pmb{x}_n, c_n \}\) and unlabeled \(\{x_l^*\}\) datasets learn model parameters

\begin{split} q_{k+1}(z_l) &\propto e^{\left < \ln p_{\pmb{\theta}_{z_n}}(\pmb{x}_l^*) \right>_{q_k(\pmb{\theta}_{z_l})} + \left< \ln p_{\pmb{\rho}}(z_l) \right>_{q_k(\pmb{\rho})} } \\ q_{k+1}(\pmb{\theta}_z) &\propto p(\pmb{\theta}_z|\{\pmb{x}_n, c_n\})e^{\sum_n q_{k+1}(z_l=z)p_{\pmb{\theta}_z}(\pmb{x}_l^*)} \\ q_{k+1}(\pmb{\rho}) &\propto p(\pmb{\rho}|\{\pmb{x}_n, c_n\}) e^{\sum_n \sum_{z_l} q_{k+1}(z_l) \ln p_{\pmb{\rho}} (z_l)} \end{split}

c_l^* = \argmax_i \frac{e^{\bar{\pmb{\theta}}^0_{i} \pmb{x}_l^* + b_{i}} }{\sum_k e^{\bar{\pmb{\theta}}^0_k \pmb{x}_l^* + b_{k}}}

2. Predict labels for the unlabeled dataset as

Gaussian mixture model

\pmb{T}(\pmb{x}) = (\pmb{x}, \pmb{x}\pmb{x}^T) \\ \pmb{\theta}_z = (\pmb{\Sigma^{-1}} \pmb{\mu}_z, - \frac{1}{2} \pmb{\Sigma}^{-1})

Normal-Inverse-Wishart prior

p(\pmb{\Sigma}^{-1}) \prod_{z} p(\pmb{\mu}_z|\pmb{\Sigma}^{-1}) = \\ \mathcal{W}(\pmb{\Sigma}^{-1}; \pmb{V}_0, \nu_0) \prod_z \mathcal{N}(\mu_z; 0, (\kappa_0 \pmb{\Sigma}^{-1})^{-1})

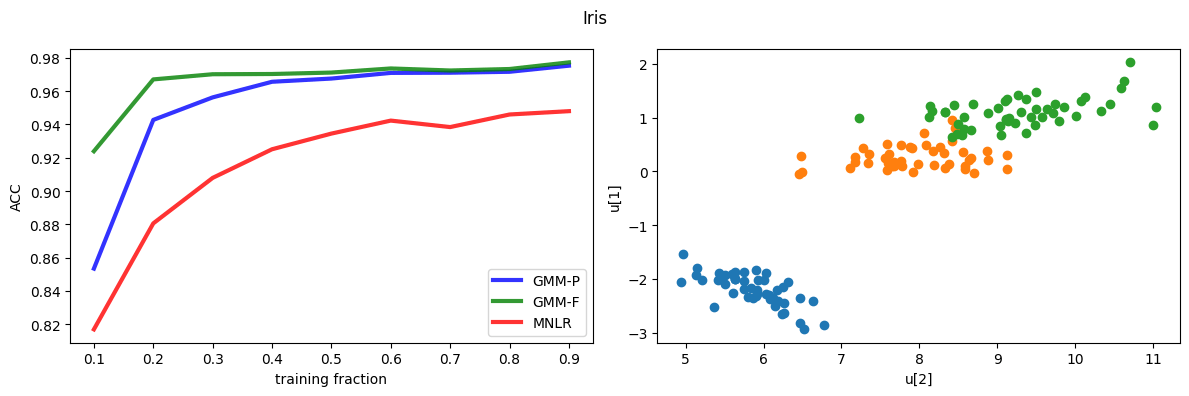
Comparison

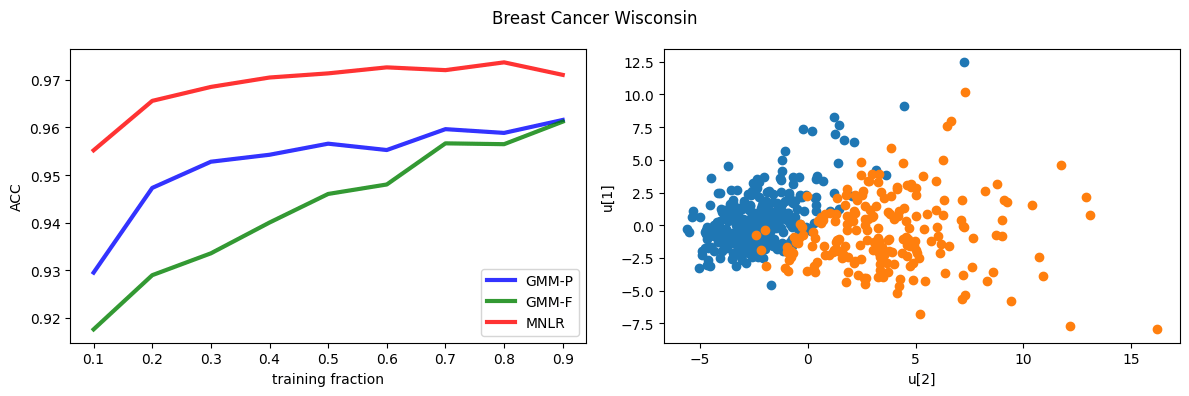
Mixture of mixtures

p_{\pmb{\theta}}(\pmb{x}_n) = \sum_{c_n} p_{\pmb{\theta}}(c_n) \sum_{z_n} p_{\pmb{\theta}}(z_n|\pmb{u}_n, c_n) p_{\pmb{\theta}}(\pmb{u}_n| c_n)p_{\pmb{\theta}}(\pmb{x}_n| \pmb{u}_n, z_n, c_n)

\pmb{T}(\pmb{x}) = \left( \pmb{x}, \pmb{f}_1(\pmb{x}), \pmb{f}_2 (\pmb{x}), \ldots \right) \\ \pmb{\theta}_{z, c}(\pmb{u}_n) = \left(\pmb{\theta}^0_{z, c}(\pmb{u}_n), \pmb{\theta}^1, \pmb{\theta}^2, \ldots \right)

c_n^* = \argmax_i \frac{e^{\bar{\pmb{\theta}}^0_{i, n} \pmb{x}_n^* + b_{i, n}} }{\sum_k e^{\bar{\pmb{\theta}}^0_{k, n} \pmb{x}_n^* + b_{k, n}}}

Prediction

parameters become a function of datapoints

Example

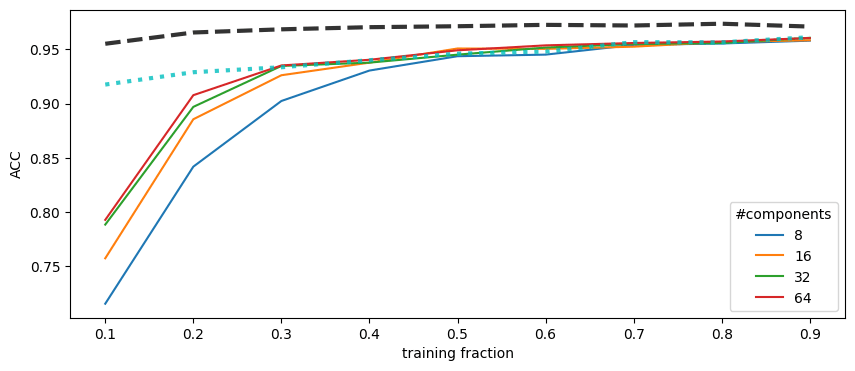
can we improve GM approach with sparse structural priors?

NNs as hierarchical MMs

\begin{split} \text{ReLU}(x) &= x h(x) \\ \text{swish}(x) &= x \sigma(x) \end{split}

\text{swish}(x) = \sum_{z \in \{0, 1\}} \int \text{d} u u p(u|x, z) p(z|x)

p(x|z, u) p(u|z) p(z)

Generative model

rsLDS

\prod_{t=1}^T p(y_t|x_t) p(x_t|z_t, x_{t-1})p(z_t|x_{t-1}, z_{t-1})

Linderman, Scott, et al. "Bayesian learning and inference in recurrent switching linear dynamical systems." Artificial intelligence and statistics. PMLR, 2017.