AI 101

HMIA 2025

https://slides.com/djjr/hmia2025-ai-bootcamp

AI 101

HMIA 2025

Goals

Demystify some terms. Fill in some gaps. Not exactly "big picture" but "starting picture." Meet 30 people at 30 different places.  Apologies to those who know way more than I do.

THERE ARE NO SILLY QUESTIONS.

I don't have all the answers.

AI 101

HMIA 2025

"Readings"

Video: Introduction to Machine Learning [3m21s]

Video: The History of Machine Learning [4m57s]

Video: Intro to Machine Learning (ML Zero to Hero - Part 1) [7m17s]

Video: Large Language Models Explained Briefly [7m57s]

Activity: Networks of Neurons

Activity: Teachable Machine

PRE-CLASS

CLASS

Outline

  1. Programing vs Machine Learning
  2. AI landscape
  3. How machines learn
  4. Training/Deployment; pretraining/finetuning; supervised/unsupervised; RL/RLHF; loss & optimization
  5. Perceptron, neuron, layers, forward, backward
  6. Accuracy, precision, reliability, validity
  7. Bias/fairness
  8. Alignment

HMIA 2025 AI Bootcamp

HMIA 2025 AI Bootcamp

HMIA 2025 AI Bootcamp

https://youtu.be/6mSx_KJxcHI?feature=shared

PRE-CLASS

HMIA 2025 AI Bootcamp

PRE-CLASS

HMIA 2025 AI Bootcamp

https://youtu.be/N6wxM4wZ7V0?feature=shared

PRE-CLASS

HMIA 2025 AI Bootcamp

PRE-CLASS

Intro to Machine Learning (ML Zero to Hero - Part 1) [7m17s]

HMIA 2025 AI Bootcamp

https://youtu.be/KNAWp2S3w94?feature=shared

PRE-CLASS

HMIA 2025 AI Bootcamp

PRE-CLASS

HMIA 2025 AI Bootcamp

Text

https://www.youtube.com/watch?v=LPZh9BOjkQs

3Blue1Brown: Large Language Models Explained Briefly [7m57s]

PRE-CLASS

HMIA 2025 AI Bootcamp

PRE-CLASS

HMIA 2025 AI Bootcamp

PRE-CLASS

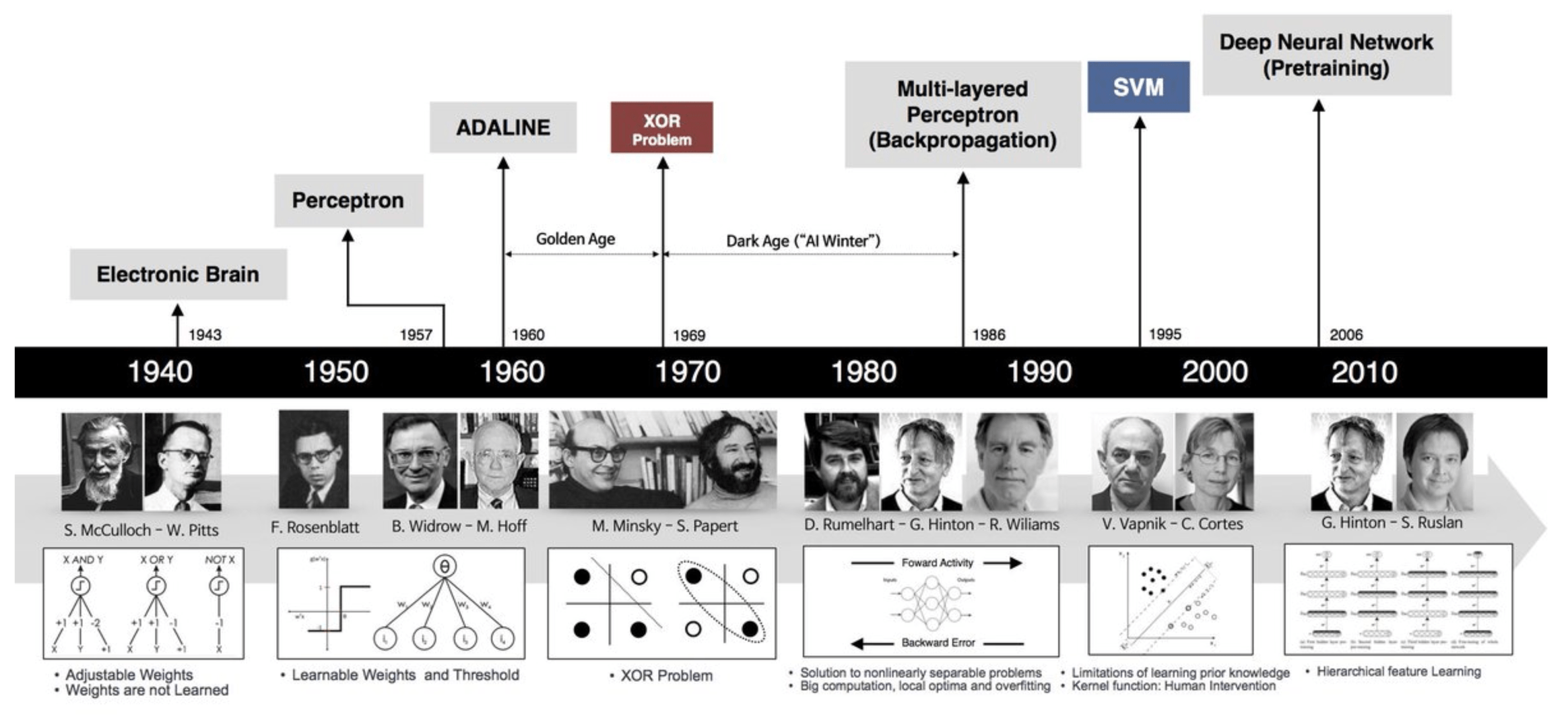
History

HMIA 2025 AI Bootcamp

CLASS

Models

HMIA 2025 AI Bootcamp

CLASS

Models

HMIA 2025 AI Bootcamp

CLASS

\hat{Y} = m X + b

m

b

X→

→Y

a black box with two dials

prediction

data

parameters

error/loss

Brains Can Be Built of Biological Neurons

HMIA 2025 AI Bootcamp

CLASS

Inputs

Output

f(\text{dendrites})

dendrites

axon

nucleus

Models Can Be Built of Artificial Neurons

HMIA 2025 AI Bootcamp

CLASS

Inputs

Output

1

0

f(1,0)

Models as Functions

HMIA 2025 AI Bootcamp

CLASS

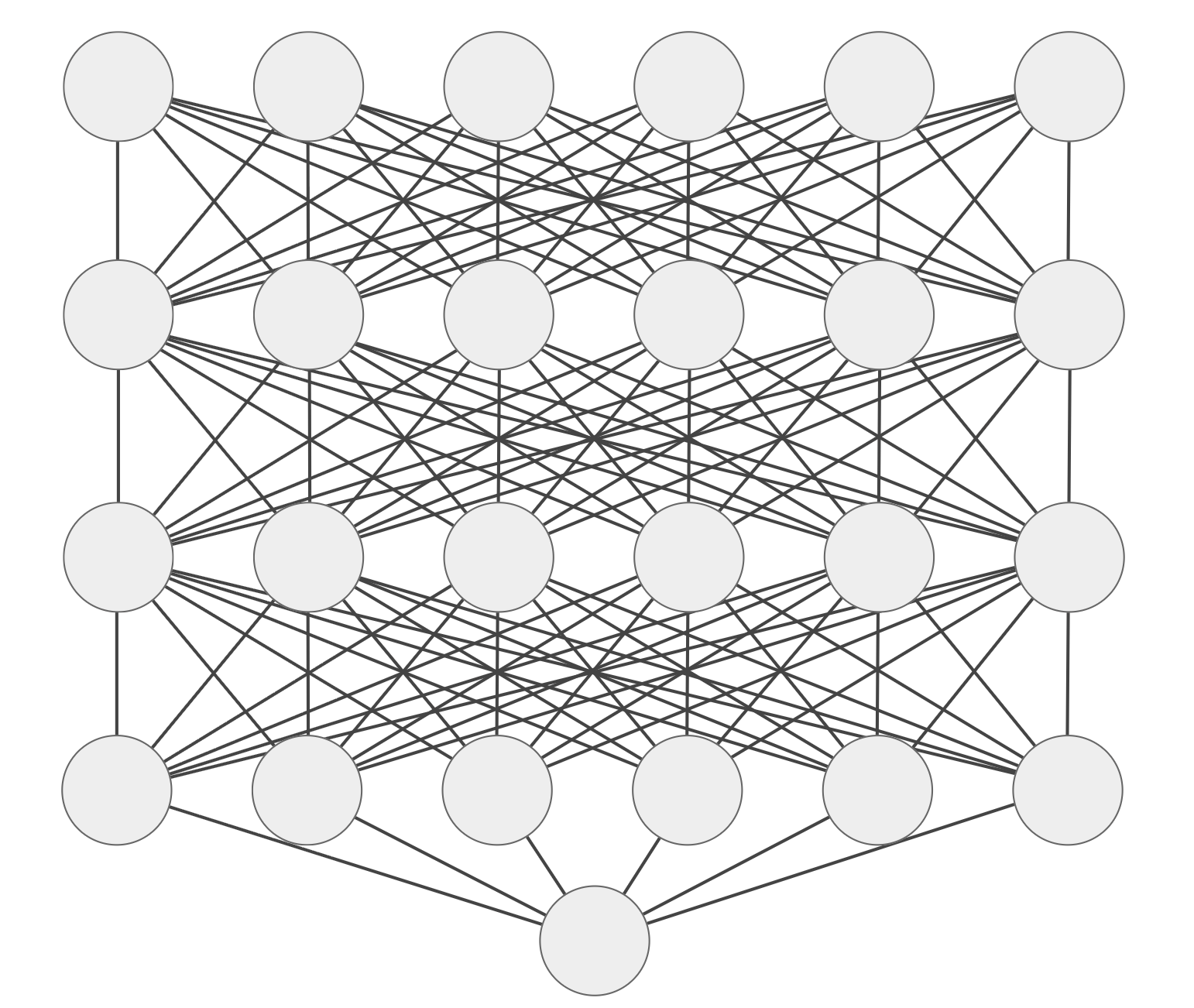
Input

Hidden Layers

Output

X_1
X_2
X_3
X_4
X_5
X_6
\hat{Y} = f(x_1,x_2,x_3,x_4,x_5,x_6)

weights (that's what's "learned")

Deep (multiple hidden layers)
Neural (each node an artificial neuron)

Network

Why Linear Algebra?

HMIA 2025 AI Bootcamp

CLASS

Input

Hidden Layers

X_1
X_2
X_3
X_4
X_5
H_1 = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{bmatrix}
h_{11} = x_1 w_{11} + x_2 w_{12} + x_3 w_{13} + x_4 w_{14} + x_5 w_{15}
w_{11}
w_{12}
w_{13}
w_{14}
w_{15}
\begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} & w_{15} \\ w_{21} & w_{22} & w_{23} & w_{24} & w_{25} \\ w_{31} & w_{32} & w_{33} & w_{34} & w_{35} \\ w_{41} & w_{42} & w_{43} & w_{44} & w_{45} \\ w_{51} & w_{52} & w_{53} & w_{54} & w_{55} \end{bmatrix}

Cat Detector as Function

HMIA 2025 AI Bootcamp

CLASS

=(12,98,231,...)
(0,1)

point in super high dimensional space

f

Reinforcement Learning

HMIA 2025 AI Bootcamp

CLASS

STOP+THINK

What else about learning to ride a bike strikes you as interesting? Do you think it's important that it's fun?  Is it important that mom is there?

Living is One Fork in the Road After Another

https://devblogs.nvidia.com/deep-learning-nutshell-reinforcement-learning/ (Video courtesy of Mark Harris, who says he is “learning reinforcement” as a parent.)

 

Agent Models

Reinforcement Learning with Human Feedback

(RLHF)

Remember the other day when we talked about having "other people in our head"?

Train your model to produce outputs from inputs.

Let it run on a lot of different inputs and rate the outputs.

Build a model that predicts the rating of each output, given a particular input.

IMAGES

0.17
0.01
0.17
0.07
0.38
0.07
0.14

Try out everything over and over and over again and keep track of how everything works out each time.

The Plan

What can models do?

HMIA 2025 AI Bootcamp

CLASS

Classify: "look" at an item and put it in a category

Predict: "look" at some information and say what comes/happens next

Optimize: "look" at situation, objective, and resources and choose best solution

Generate: "look" at a description, create a text or image or sound

Translate: "look" at something in one form and transform it to another form

 

Networks of Neurons

HMIA 2025 AI Bootcamp

CLASS

Imagine you are a worm learning how to move around in the world.  You are constantly bumping into things. Some things are sharp and threatening. You can defend yourself against sharp, threatening things by curling into a ball.  But if you curl into a ball everything something touches you, all the other worms will laugh and you'll never get anywhere.

So you have this neuron that responds to touch
and drives the curl-up action in response.  How                does the worm train                                                 the neuron to respond to the proper levels of touch (only curl                       up when you                                                         encounter a sharp and threatening touch)?

Let's suppose the neuron works like this: the input is                      a measure of                                             the touch; this is compared to a threshold and if it is higher, the neuron                                  triggers                      a curl-up action.

Initially, the threshold is zero: the worm curls up at the                                                            slightest touch.  This happens a few times, touches of level 1 and level 2 and level 9, and the                                                          worm notices that nothing happened, the touch did not cause any harm.  So, it raises                                                     the threshold to 1.  Now when it gets a level 1 touch it just keeps moving. But level 2 touches                                                  cause it to curl up.  And then some 5s and 6s and it curls up.  Again, it notices that nothing happened so it                                                                   raises the threshold to level 2.

This continues for a bit and it has raised the threshold to level 6. Then
one day, it gets a level 5 poke that really hurts — a sharp thorn or a
hidden barb.  So the worm lowers its threshold by 1 to level 5.  Now it curls up when it feels a level 5 poke.  For a while, it seems to be avoiding injury quite well so it lowers the threshold to 4. Then it notices that sometimes a level 5 poke is painful but sometimes not and so it leaves the threshold at 4. The worm has learned an approximate rule: curl up when things feel like level 5 or higher — but not always, and not perfectly.

HMIA 2025 AI Bootcamp

CLASS

We all know about the game of guessing the number of jelly beans in a jar.  And if you have taken a statistics you have heard of the "wisdom of the crowd" : we can ask a bunch of people to estimate and then we take the average of their guesses.

Could we teach a machine to learn how much to
trust each person’s guess — and adjust based
on feedback?

 

ROUND 1. Present the jar, record the guesses,
compute the average, reveal the actual number of
jelly beans.

Remind ourselves that computing the average is
the same as computing a weighted sum where the weights are all 1/n where n is the number of people guessing. We count the number of folks in the room
and compute 1/n. "This is your initial weight."

ROUND 2. We ask for show of hands: how many had a guess that was high? Low?  If your guess last round was higher than the actual number, subtract 0.05 from your weight. If it was lower, add 0.05. ​

If you were spot-on, leave it as is.

Now we introduce a new jar and ask folks to write down their guess.

  We have folks do a little math - multiply their
  guess times their weight - and we add up all the results.

   Then we reveal the actual number of jelly beans.

    ROUND 3. We repeat the process.
 

  STOP+THINK. What's going to happen to folks who consistently guess too low?

 

We can introduce some limits like "your weight can never go above 1 or below 0.  Or, after we increment or decrement everyone's weights we could adjust them all so they still add up to 1. This would preserve the math of the weighted average.

STOP+THINK. Would it be better to add/subtract more weight from people who were really far off, and less from those who were just a little off?

HMIA 2025 AI Bootcamp

CLASS

HMIA 2025 AI Bootcamp

\frac {1}{5} \times 200 + \frac {1}{5} \times 150 + \frac {1}{5} \times 250 + \frac {1}{5} \times 250 + \frac {1}{5} \times 150 = 200
\text {Actual} = 220
\begin{aligned} & \text{New Weights: } 0.25, 0.25, 0.15, 0.15, 0.25 \end{aligned}
\text {Actual} = 400
\begin{aligned} & \text{New Guesses: } 300, 350, 450, 500, 500 \end{aligned}
\begin{aligned} & \text{New Weighted Average } \\ &= 300 \times 0.25 + 350 \times 0.25 + 450 \times 0.15 + 500 \times 0.15 + 500 \times 0.25 \\ &= 75 + 187.5 + 67.5 + 75 + 125 = 455 \end{aligned}
\begin{aligned} & \text{New Weights: } 0.3, 0.3, 0.1, 0.1, 0.2 \end{aligned}
\text {Actual} = 150
\begin{aligned} & \text{New Guesses: } 100, 150, 250, 200, 300 \end{aligned}
\begin{aligned} & \text{New Weighted Average } \\ &= 100 \times 0.3 + 150 \times 0.3 + 250 \times 0.1 + 200 \times 0.1 + 300 \times 0.2 \\ &= 30 + 45 + 25 + 20 + 60 = 180 \end{aligned}
\begin{aligned} & \text{Guesses: } 200, 150, 250, 250, 150 \end{aligned}

low

high

high

low

low

CLASS

HMIA 2025 AI Bootcamp

\begin{aligned} & \text{Guess: } 100 \end{aligned}
\begin{aligned} & \text{Guess: } 300 \end{aligned}
\begin{aligned} & \text{Guess: } 200 \end{aligned}
\begin{aligned} & \text{Guess: } 250 \end{aligned}
\begin{aligned} & \text{Guess: } 150 \end{aligned}
\begin{aligned} & \text{Weight: } 0.3 \end{aligned}
\begin{aligned} & \text{Weight: } 0.2 \end{aligned}
\begin{aligned} & \text{Weight: } 0.1 \end{aligned}
\begin{aligned} & \text{Weight: } 0.1 \end{aligned}
\begin{aligned} & \text{Weight: } 0.3 \end{aligned}
\begin{aligned} & \text{New Weighted Average } \\ &= 100 \times 0.3 + 150 \times 0.3 + 250 \times 0.1 + 200 \times 0.1 + 300 \times 0.2 \\ &= 30 + 45 + 25 + 20 + 60 = 180 \end{aligned}

CLASS

Models as Functions

HMIA 2025 AI Bootcamp

CLASS

Input

Hidden Layers

Output

X_1
X_2
X_3
X_4
X_5
X_6
\hat{Y} = f(x_1,x_2,x_3,x_4,x_5,x_6)

Models

HMIA 2025 AI Bootcamp

CLASS

Google has a cool online tool called Teachable Machine that let's you train a computer vision model in your browser.

Go to the Teachable Machine site and train a model to distinguish between something and something else.

HMIA 2025 AI Bootcamp

CLASS

HMIA 2025

NEXT Alignment Bootcamp