LOGIC


Logic
NOTES from google drive
Logic II

STOP+THINK.
How many rows in the truth table for this expression?
VW!XY || !VWZ || VWYZ || VW!XYZ
5031
STOP+THINK.
How many rows in the truth table for this expression?
VW!XY || !VWZ || VWYZ || VW!XYZ
Count the variables: V, W, X, Y, and Z - five total.
Therefore we need 25=32 rows.
Part I
Motivation
you want to build a number displaying machine
Tutorial
Prep
- y = f(x)
- CSS classes
- another page element property (classname)
- JavaScript "switch"
We have set up a shell with some HTML, CSS, and JS. Here's what happened behind the scenes:
Create 10 buttons in the <div> each of which sends a single digit to a function called "display(x)"
Create a <div> ("division") element to contain our button pad
Add <br /> ("line break") tags to create "line breaks" so we see three buttons per line
Create a table in HTML with 5 rows and 3 columns that we can use for the seven segment display.
Give the seven table cells that will be part of the 7 segment display the ids A through G.
Give the table cells A, G, and D the class "horizontal" and cells B, C, E, F the class "vertical" so that we can use CSS to style them
Instructions 1
Create the classes vertical and horizontal in CSS
.vertical {
width: 20;
height: 60;
background-color: red;
}.horizontal
{
width: 60;
height: 20;
background-color: red;
}

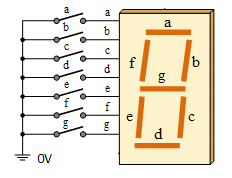

off on on off off off off
on off on on off on on
on on on on on on on
Think Slowly
Start Simply
Can we design a digital electronic machine to do this?
Imperfect Analogy




ANALOG - CONTINUOUS
DIGITAL - DISCRETE
ANALOG - CONTINUOUS
DIGITAL - DISCRETE



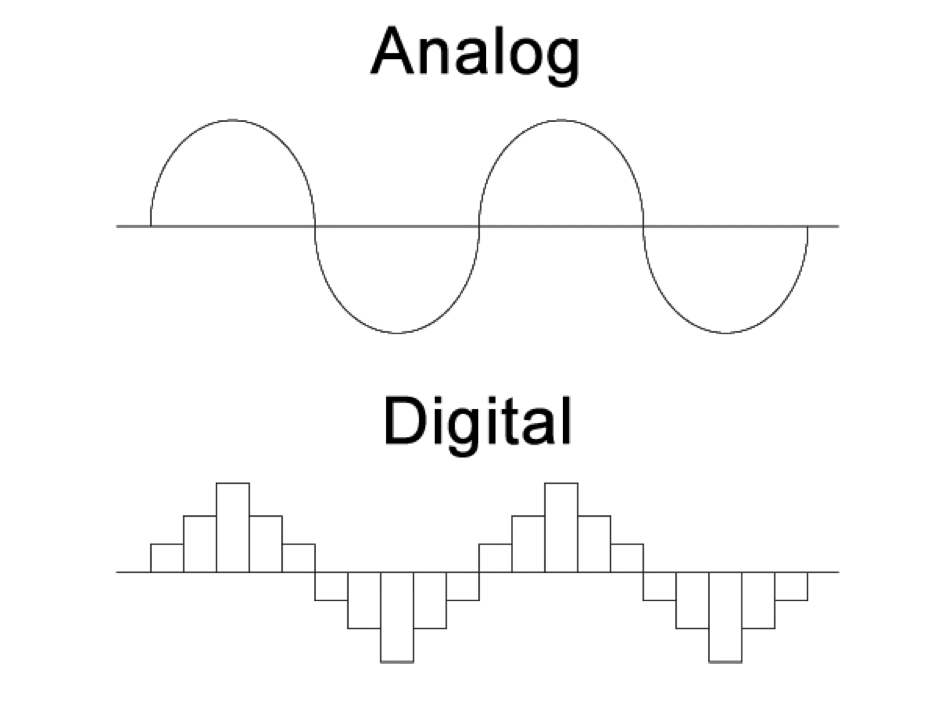

analog
digital
input
output











4 input bits
4 input bits
5 output bits
push button switches
Tools We Already Have
- Binary output from each key


?
Agenda
- Logic
- Circuits
Review

Review
Statement: sentence that can be true or false
Logical expression: combination of logical variables and operators
LOGIC 101
My name is Dan.


My name is Dan.
value = TRUE
value = FALSE
A = it is sunny out
A?
A = it is sunny out
A?
A is a logical variable. A name that stands for a statement or condition that can be true or false.
A LOGICAL VARIABLE CAN TAKE ON ONE OF TWO LOGICAL VALUES
TRUE
FALSE
1
0
LOGICAL VARIABLES can be combined
with LOGICAL OPERATORS
such as AND, OR, and NOT
to form LOGICAL EXPRESSIONS
which also can only be TRUE or FALSE
D = A and B
E = A and C
F = A or B
G = not C
H = B and not C
I = not A or not C
TRUE
TRUE
TRUE
TRUE
TRUE
FALSE
STOP+THINK
-
Consider the three expressions below as articulated by your instructor:
A = "My name is Dan."
B = "At the moment, I am in Toronto."
C= "I am a dog."
Which of the following logical expressions is true?

LOGICAL OPERATORS
- "Binary" Operators (connecting two values)
- AND
- OR
- "Unary" Operator (works on just one value)
- NOT
Alternative Notations
A and B also written AB, A∧B, A·B, A && B
A or B also written A+B, A∨B, A || B
not A also written ~A, !A, ¬A, Ā
Definitions I
W is true if both A, B are true
W is
true when A is false,
false when A is true
W = A or B
W = A and B
W is true if either or both A,B truee
W = not A
Boolean Algebra: the "math" of logic
- akin to multiplication
- AB, A∧B, A·B
-
1 or TRUE is identity
- X AND TRUE = X
- X·1=X for any X
Only two "numbers": 0 and 1
Three "operations":
AND
- akin to addition
- A+B, A∨B
-
0 or FALSE is identity element
- X or FALSE = X
- X+0=X
- akin to negation
- ~A, !A, ¬A, Ā
- not 0 = 1, not 1 = 0
OR
NOT
2. Match expressions on left with notation on the right
A∨B
A·B
A∧B
AB
A+B
A OR B
A and B
A && B
A||B
STOP+THINK
Match
A∨B
Ā
A·B
A∧B
AB
A+B
A OR B
~A
!A
¬A
A and B
A && B
A||B
Boolean Algebra: the "math" of logic
AND takes precendence over OR
AB + C
means "A and B ... or C"
not "A and ... B or C"
but use parentheses to say otherwise
A(B + C)
means "A and ... B or C"
Boolean Algebra: the "math" of logic
AND "distributes" over OR
A(B + C) = AB + AC
Boolean Algebra: the "math" of logic
common vars can be "factored out: of ORs
AB + AC = A(B + C)
STOP+THINK
3. Is the middle expression the same as the one on the left or the one on the right?
| (ABC) + D | ABC+D | AB + CD |
| ((ABC)+(ABD))E | AB+CD E | (AB)+(CDE) |
| (A+!A)(B) | A!B+AB | A(!B+B) |
| AC+BD | AB(C+D) | ABC+ABD |
Boolean Algebra: the "math" of logic
Since 1/0 are exhaustive
A + !A = TRUE
Since 1/0 are mutually exclusive
A · !A = FALSE
Putting a Few Results Together
A + !A = TRUE
AB + AC = A(B+C)
A · TRUE = A
AB + A!B = A
AB + A!B = A(B+!B)
AB + A!B = A(TRUE)
AB + A!B = A
Boolean Algebra: the "math" of logic
Summary so far
A + !A = TRUE
A · !A = FALSE
AB + AC = A(B + C)
A(B + C) = AB + AC
X·1 = X for any X
X+0 = X for any X
STOP+THINK
4. Simplify this expression using the AB+A!B=A rule.
!AB + A!C + AC + !A!B
!AB + (A!C + AC) + !A!B
!AB + A(!C + C) + !A!B
!AB + A + !A!B
A + AB + !A!B
A + !A(B + !B)
A + !A
TRUE
STOP+THINK
5. Simplify this expression using the AB+A!B=A rule.
!ABCD + !AB!CD
!ABDC + !ABD!C
!ABD(C + !C)
!ABD(TRUE)
!ABD
STOP+THINK
6. Simplify this expression using the AB+A!B=A rule.
!ABCD + ABCD + !ABC!D + ABC!D
BCD + BC!D
BC
BCD + !ABC!D + ABC!D
One More Thing
(AB)C = (AB)C
(A+B)+C = (A+B)+C
AB = BA
A+B = B+A
TRUTH TABLES
A logical expression is DEFINED by its truth table which shows its value for every possible combination of inputs
TRUTH TABLES
A truth table is simply a listing of all possible combinations for an expression along with the value of the expression for each combination.
Suppose an expression includes three variables A, B, and C.
A can be true or false
B can be true or false
C can be true or false
B can be true or false
C can be true or false
C can be true or false
C can be true or false
1
0
11
10
01
00
111
110
101
100
011
010
001
000
A
C
B
exp
TRUTH TABLES
A truth table is simply a listing of all possible combinations for an expression along with the value of the expression for each combination.
Suppose an expression includes three variables A, B, and C.
0 0 1
0 0 0
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A
C
B
exp
"expression" - we'll put the value of the expression for each input combination here
TRUTH TABLES
| A | B | A+B |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
row for each
input combination
row for each
input combination
column
for each
variable
column
for "output"
TRUTH TABLES
| A | B | A+B |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| A | B | C |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 0 | 0 | 0 |
| A | B | C | D |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 |
all the 1's for the first varible
{
all the 0's for the first varible
{
all the 1's for the first varible
{
all the 0's for the first varible
{
all the 0's for the first varible
all the 1's for the first varible
| A |
|---|
| 1 |
| 0 |
| A | B |
|---|---|
| 1 | 1 |
| 1 | 0 |
| 0 | 1 |
| 0 | 0 |
| A | B | C |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 0 | 0 | 0 |
| A | B | C | D |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 |
Definitions II
| A | B | AB |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
AND
| A | B | A+B |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
OR
| A | !A |
|---|---|
| 1 | 0 |
| 0 | 1 |
NOT
7. Example: Build Truth Table for !A + B
A
B
1
1
0
0
1
0
1
0
!A
!A+B
1
B
1
0
1
0
0
0
1
1
0
1
1
STOP+THINK
8. Build Truth Table for !A!B + BC
| A | B | C |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 0 | 0 | 0 |
!A!B
| 1 |
| 1 |
| 1 |
| 1 |
BC
+
| !A |
|---|
| 0 |
| 0 |
| 0 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| !B |
|---|
| 0 |
| 0 |
| 1 |
| 1 |
| 0 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
STOP+THINK
8. Example: Build Truth Table for !A!B + BC
A
B
C
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
!A
!B
!A·!B
B·C
!A!B+BC
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
Boolean Algebra: the "math" of logic
AND "distributes" over OR
A(B + C) = AB + AC
| A | B | C | A | and | B+C | AB | + | AC |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 0 | ||||
| 0 | 1 | 1 | 1 | |||||
| 0 | 1 | 0 | 1 | |||||
| 0 | 0 | 1 | 1 | |||||
| 0 | 0 | 0 | 0 |
| A | B | AB | !(AB) | !A | + | !B | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | ||||||
| 1 | 0 | ||||||
| 0 | 1 | ||||||
| 0 | 0 |
!(AB)
= !A+ !B
| A | B | A+B | !(A+B) | !A | AND | !B | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | ||||||
| 1 | 0 | ||||||
| 0 | 1 | ||||||
| 0 | 0 |
!(A+B)
= !A !B
Laws
DeMorgan
!(AB) = !A+!B
!(A+B) = !A!B
Distributive
A(B+C) = AB + AC
Double negation
!!A = A
Boolean Algebra: the "math" of logic
Summary so far
A + !A = TRUE
A · !A = FALSE
AB + AC = A(B + C)
A(B + C) = AB + AC
X·1 = X for any X
X+0 = X for any X
!(A+B) = !A!B
!(A · B) = !A + !B
}
}
}
}
identity elements
distributive property
mutual exclusive + exhaustive
definition of NOT
DeMorgan's Laws
1
1
1
1
1
1
0
0
0
1
1
1
0
0
0
0
Truth tables tell what combinations of inputs make an expression true.
The expression is true if any one of these combinations occur.
A "combination" is a particular value for the first variable AND the second variable AND the third variable AND so on.
Truth table for expression can be written as
"or of ands"
where the ands are the input combinations of each row with a 1
| A | B | C | EXP |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 |
1
1
1
1
1
1
0
0
0
1
1
1
0
0
0
0
Boolean Algebra: the "math" of logic
| A | B | C | EXP |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 |
1
1
1
1
+
+
+
B
A
C
1
1
1
A
!C
!B
1
0
0
C
!A
!B
1
0
0
!C
!A
!B
0
0
0
Boolean Algebra: the "math" of logic
And, finally:
an "or of ands*" for each row with a 1
| A | B | C | EXP |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 |
1
1
1
1
1
1
1
1
0
0
1
0
0
0
0
0
+
+
+
+
+
+
B
A
C
A
!C
!B
C
!A
!B
!C
!A
!B
Part II Physical Logic
Our Motivating Problem




Push
button
Generate
4 bit signal
Send
7 bit signal
Illuminate segments
?
Claude
Shannon
1938
Logical Expressions and switching circuits are the same thing



Logic 2 Storyboard
If electricity is new territory, perhaps work through a few slides...
but first...
Imagine a one kilogram mass attached to a rope
1 kg
We lift it one meter
thereby "storing" 9.8 "joules" of energy in the mass
1 kg
1 m
9.8 joules
which we can get back by lowering the mass
1 kg
This happens because we have to do work to raise the mass because of the gravitational attraction between it and the earth
1 kg
Electrical Potential Energy VOLTS
positive and negative electric charges are attracted to one another
-
+
potential (volts)
Electrical Potential Energy VOLTS
separating positive and negative charges increases potential
-
+
potential (volts)








Batteries as voltage source

+
-
3V

Batteries in a circuit

+
-
3V


Batteries in a circuit

+
-
3V

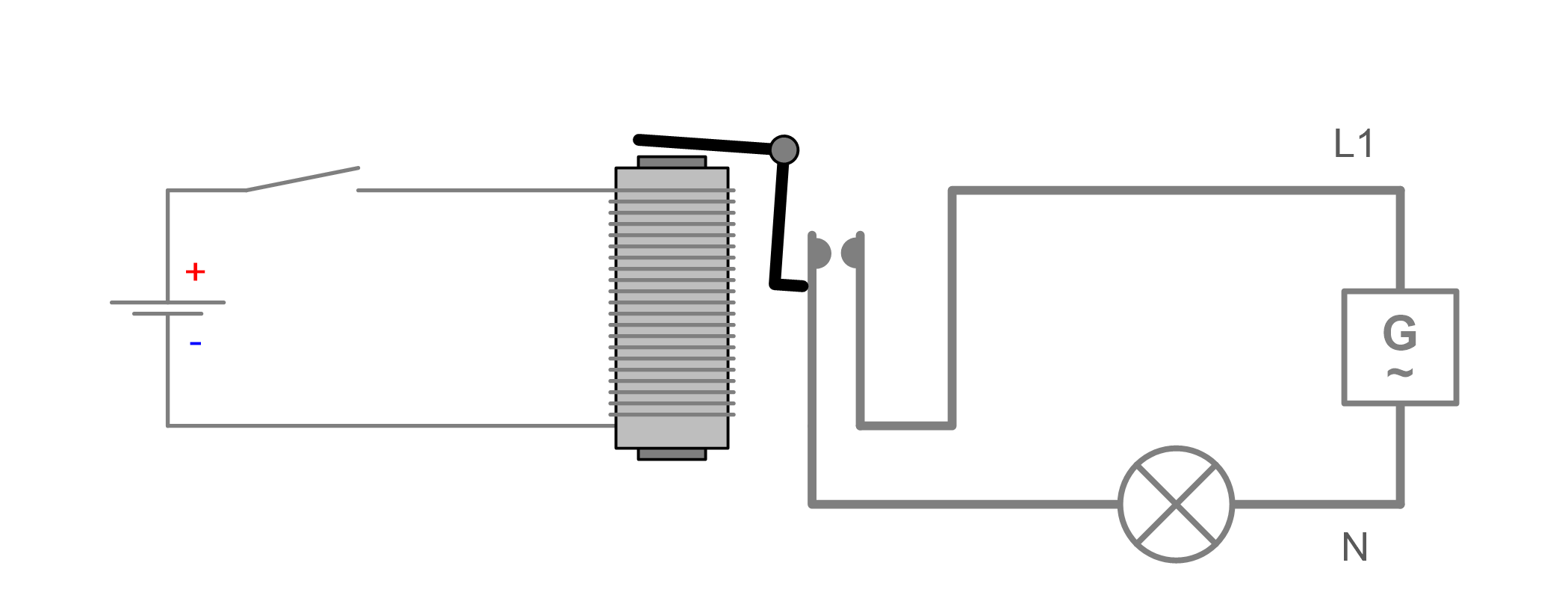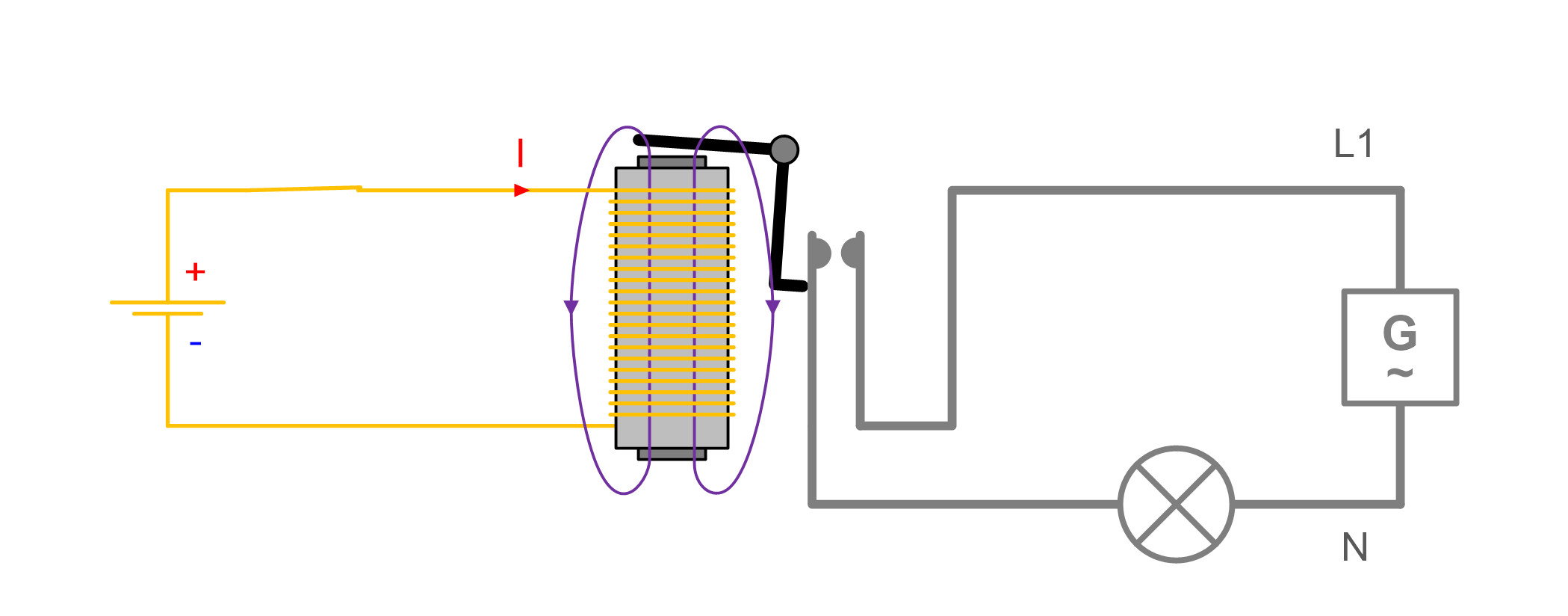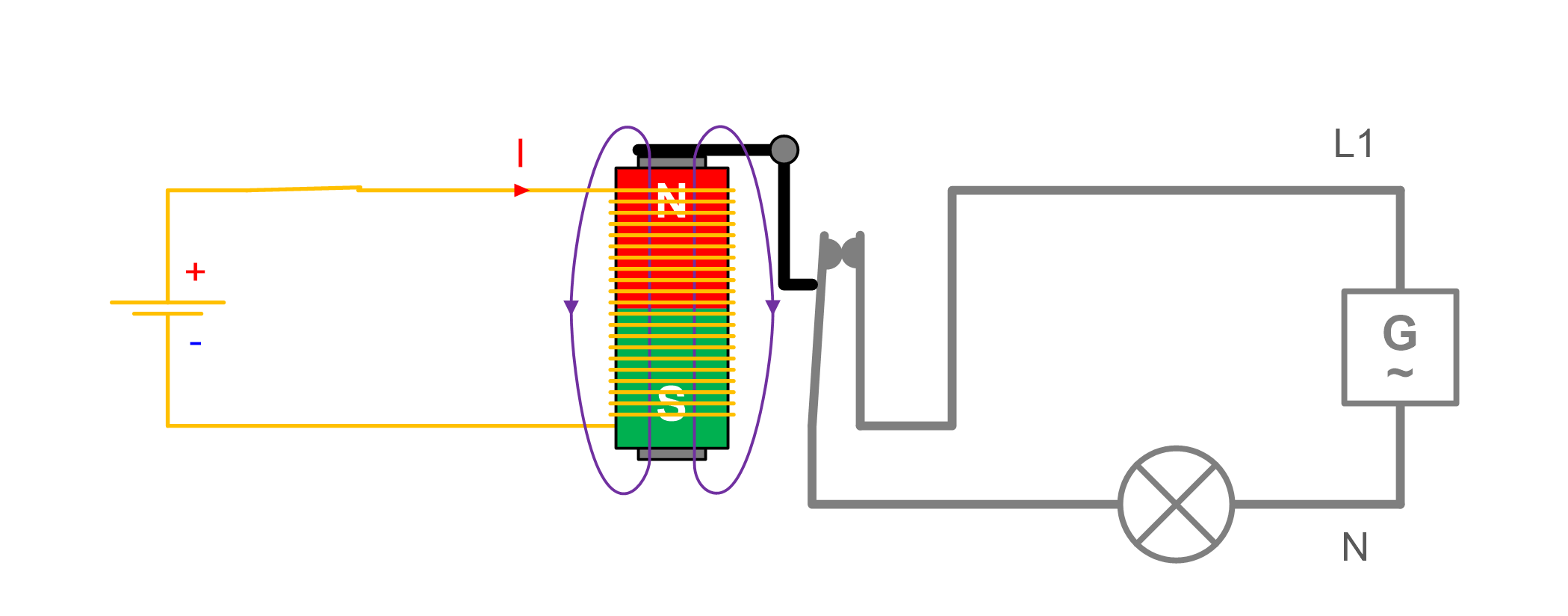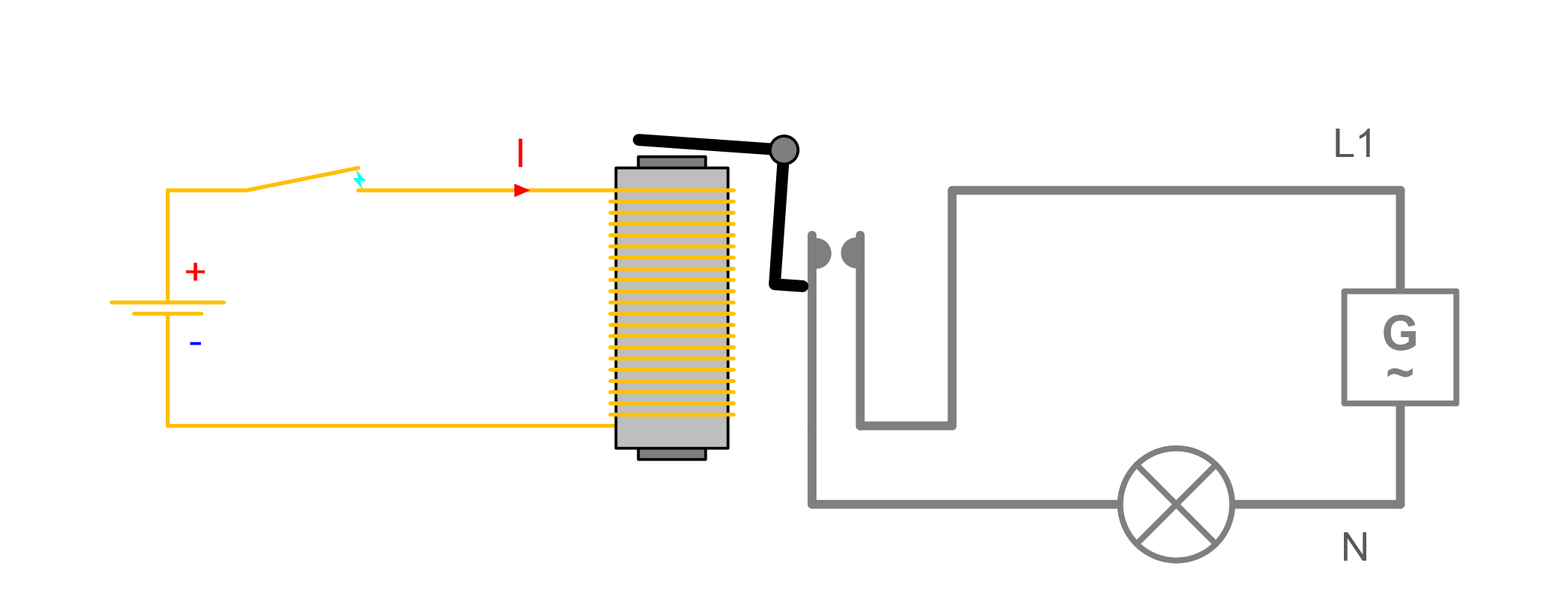
Circuit is closed. Light bulb "feels" a voltage difference
Circuit is open. Light bulb "feels" no voltage difference
Voltages in a circuit
+
3V
Circuit is closed. Light bulb "feels" a voltage difference
Circuit is open. Light bulb "feels" no voltage difference
Ground
aka
0V
By Cloullin - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=101294652
A
B
C
D
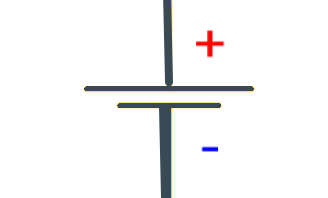
E
Logical Values + Electricity
+3 or +5 volts
0 volts
1
0
true
false
Switch and Logic
Switch and Logic
AND
AND
A and B
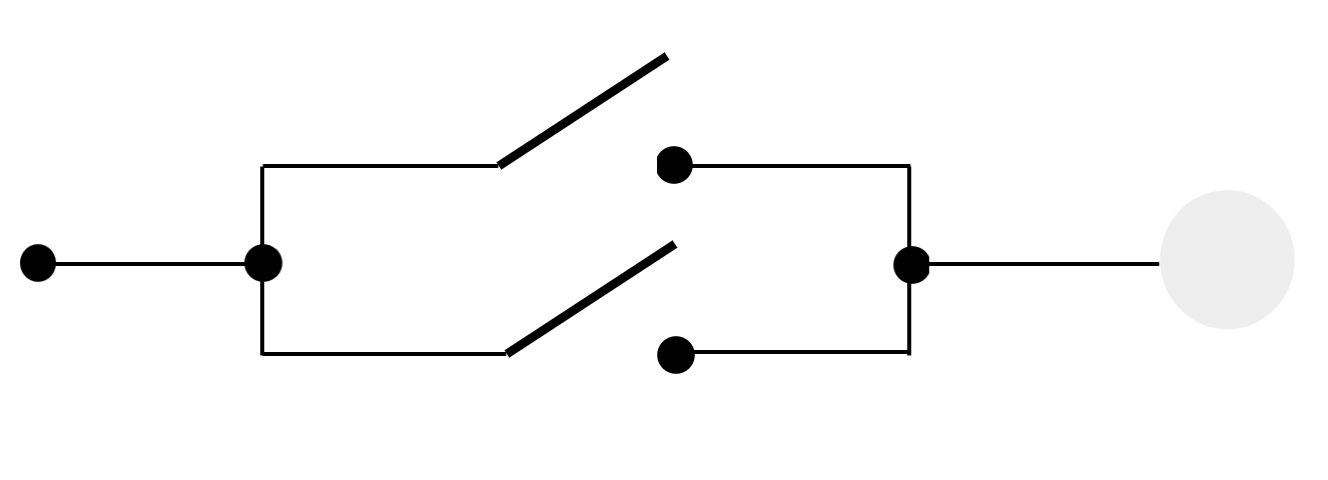

+
-
3V

A or B
Logical Operators + Switches

+
-
3V

A
B
A
B

+
-
3V

Logical Operators + Switches
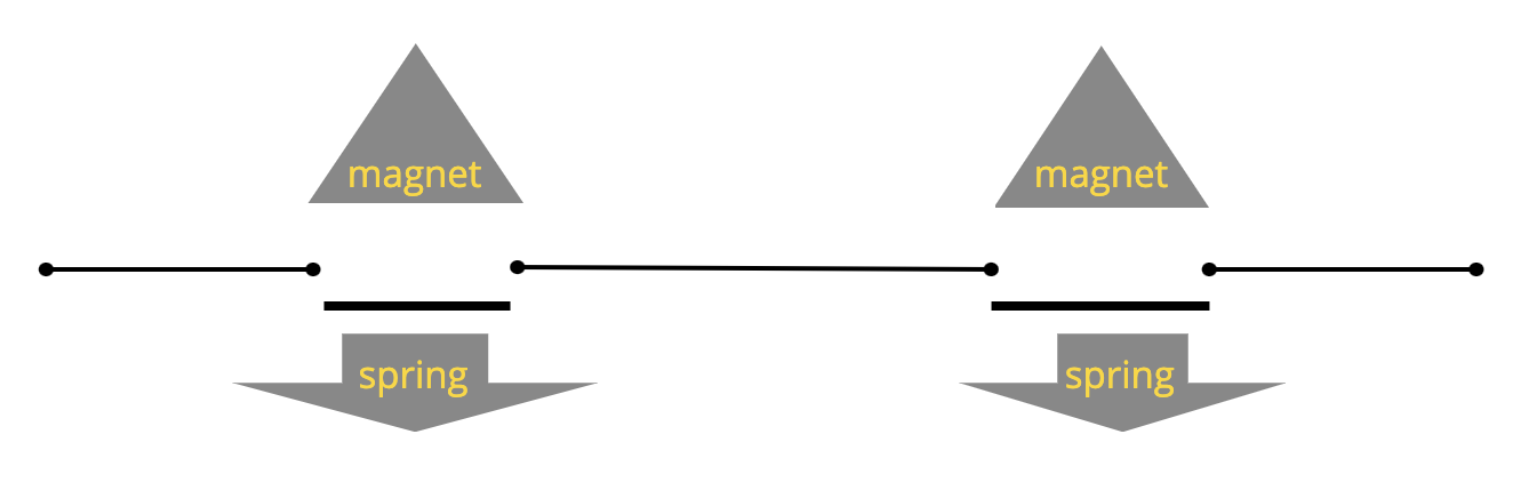
Logical Values + Switches
+3-5 volts
+3-5 volts
logical 0
logical 1
OPEN SWITCH
CLOSED SWITCH
For what it's worth: the usual value of digital "1" is +3-5 volts DC
AND, OR
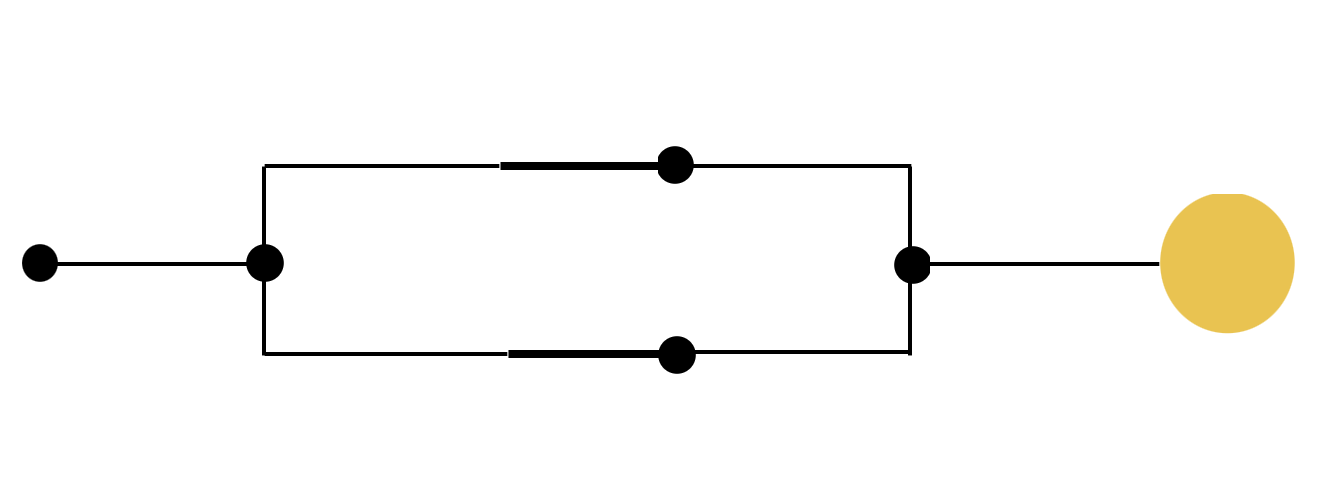
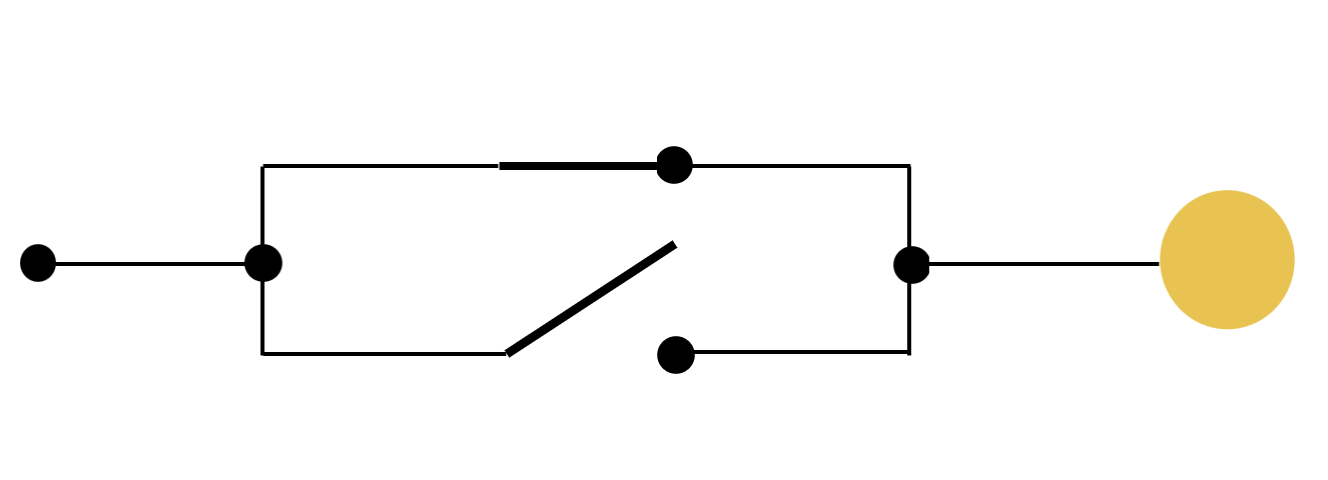
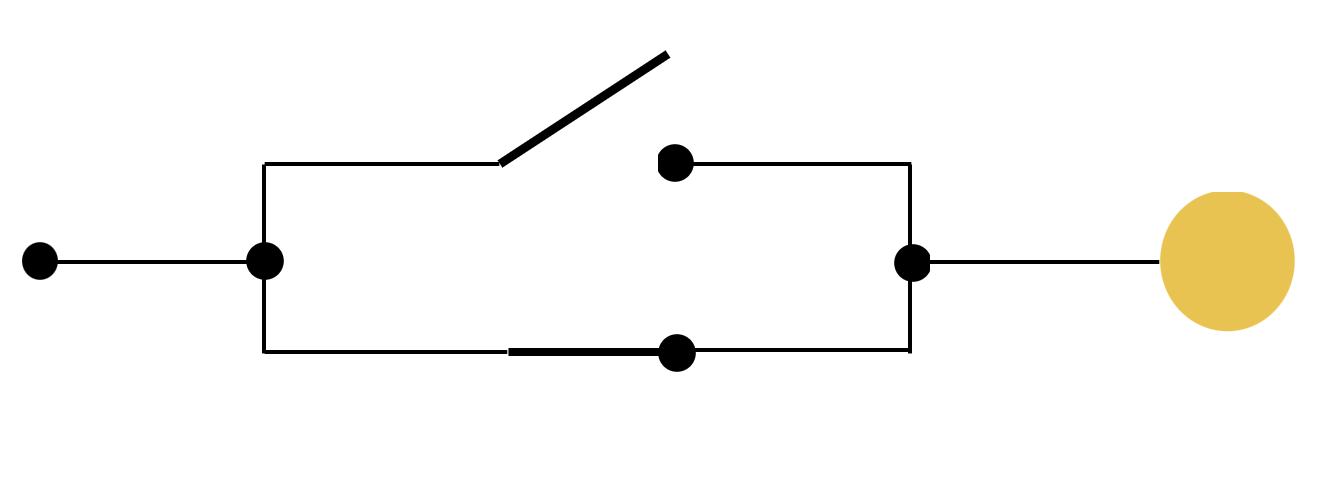

OR
NOT
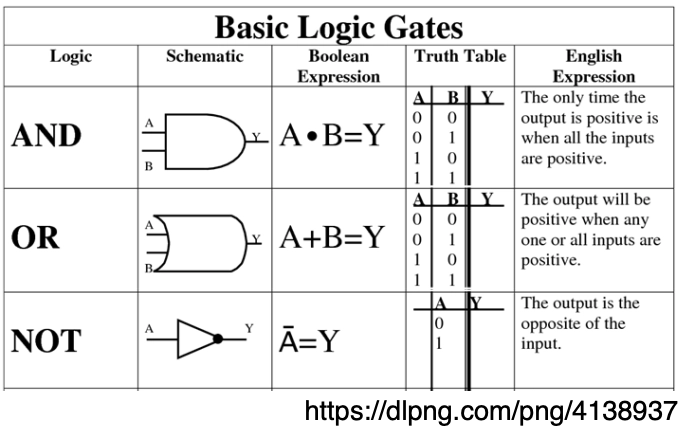
Let's Blackbox These
NOT
NOT
NOT
NOT
OR
OR

OR

OR

AND
AND

AND

AND

OR

NOT
AND

OR

NOT
AND
3V
A
B
Y
A
B
Y
A
B
Y
A
B
Y
| A | B | A and B |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |

A
B
Y
OR
A
B
Y
A
B
Y
A
B
Y
A
B
Y
| A | B | A or B |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Example
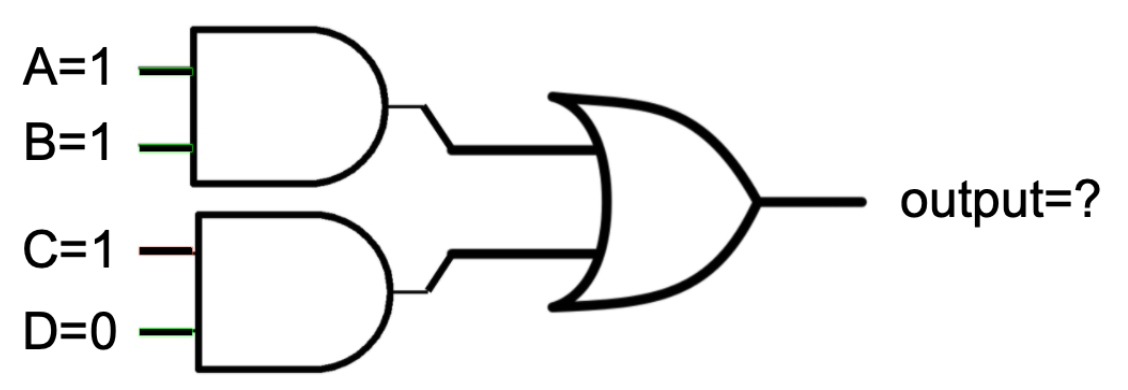
Example
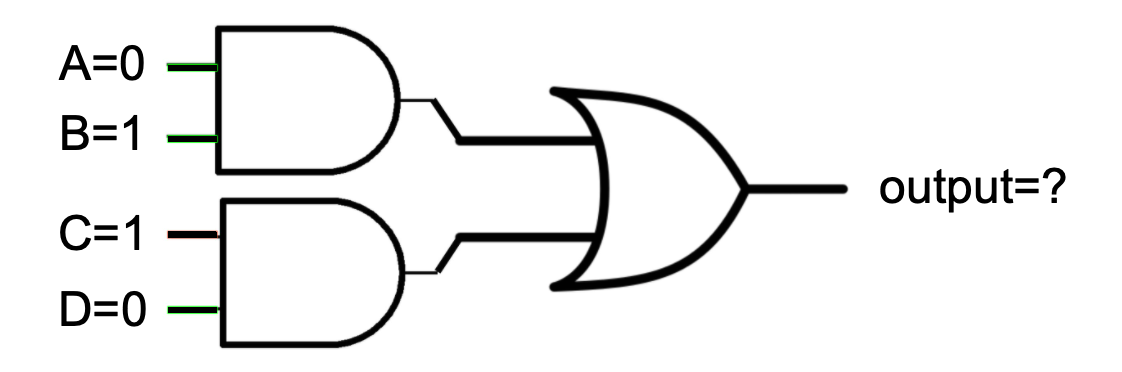
Example
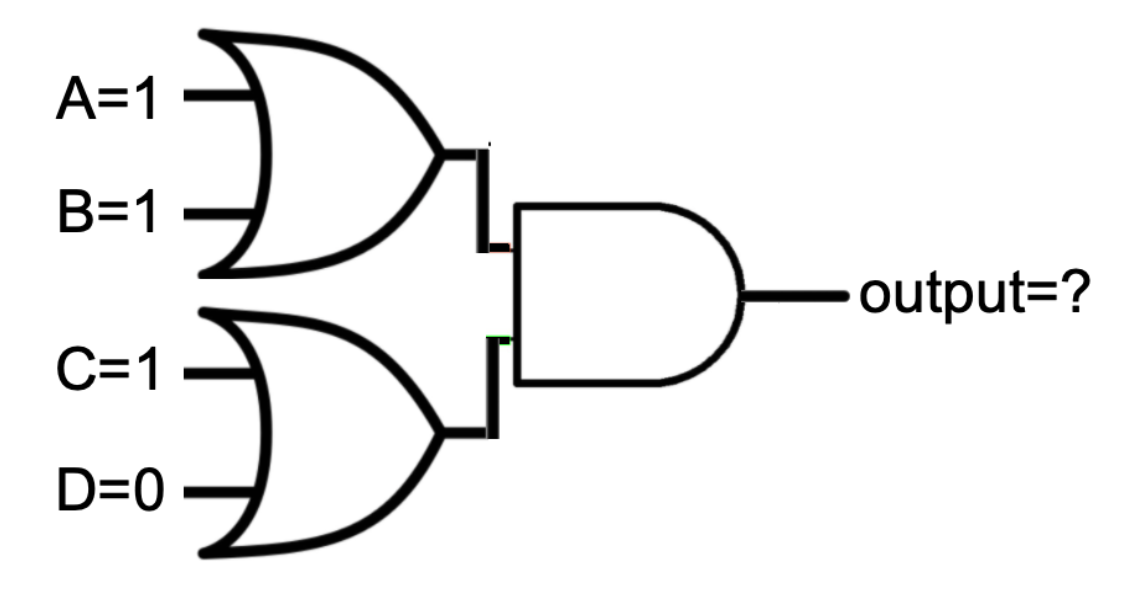
Example
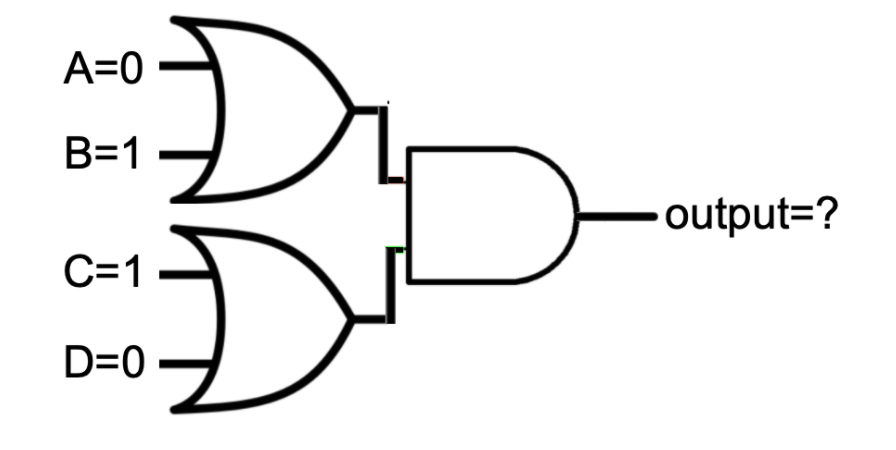
Example
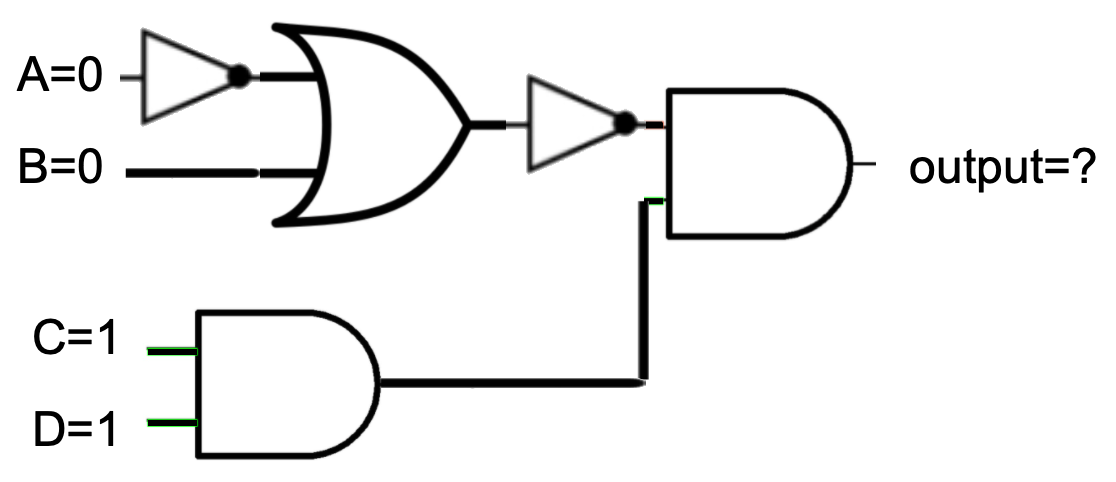



A
B
C
D



A
B
C
D
AB + CD

Simple expressions + circuits
A
B
C


A B C AB+BC
1 1 1 1
1 1 0 1
1 0 1 0
1 0 0 0
0 1 1 1
0 1 0 0
0 0 1 0
0 0 0 0
1 1 1
0 1 1
1 1 0
+
+
A
B
C



A B C AB+BC
1 1 1 1
1 1 0 1
1 0 1 0
1 0 0 0
0 1 1 1
0 1 0 0
0 0 1 0
0 0 0 0
1 1 1
0 1 1
1 1 0
+
+
ABC
!ABC
AB!C
+
+
AB
BC
+
"or of ands" from truth table
simplified expression via distributive property and A+!A=true
Simplifying Logic Expression = Simplifying Logic Circuits
AB + BC=B(A+C)
A
B
C



A
C
B


Simplifying Logic Expression = Simplifying Logic Circuits
AB + BC=B(A+C)
B
A
C


33% savings!
A
B
C



Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|
| W |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | |||
| 1 | 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | |
| NUM |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
A
B
G
D
E
C
F
Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| A |
|---|
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| NUM |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
A
B
G
D
E
C
F
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | ||||
| 10 |
WX
YZ
A!B!CD
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| A |
|---|
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| NUM |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
A
B
G
D
E
C
F
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | ||||
| 10 |
WX
YZ
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| A |
|---|
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| NUM |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | ||||
| 10 |
WX
YZ
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
+
+
+
+
+
+
+
A=
Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| A |
|---|
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| NUM |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | ||||
| 10 |
WX
YZ
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
+
+
+
+
+
+
+
A=
Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| A |
|---|
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| NUM |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | ||||
| 10 |
WX
YZ
1
1
1
1
1
1
1
1
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
+
+
+
+
+
+
+
A=
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| A |
|---|
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| NUM |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | ||||
| 10 |
WX
YZ
1
1
1
1
1
1
1
1
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
+
+
+
+
+
+
+
A=
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| A |
|---|
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| NUM |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | ||||
| 10 |
WX
YZ
1
1
1
1
1
1
1
1
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
+
+
+
+
+
+
+
A=
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| A |
|---|
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| NUM |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | ||||
| 10 |
WX
YZ
1
1
1
1
1
1
1
1
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
+
+
+
+
+
+
+
A=
Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| A |
|---|
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| -- |
| -- |
| -- |
| -- |
| -- |
| -- |
| NUM |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | ||||
| 10 |
WX
YZ
1
1
1
1
1
1
1
1
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
+
+
+
+
+
+
+
A=
Our Seven Segment Display
| W | X | Y | Z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| A |
|---|
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| -- |
| -- |
| -- |
| -- |
| -- |
| -- |
| NUM |
|---|
| O |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| X |
| X |
| X |
| X |
| X |
| X |
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | -- | -- | -- | -- |
| 10 | -- | -- |
WX
YZ
1
1
1
1
1
1
1
1
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
+
+
+
+
+
+
+
A=
Our Seven Segment Display
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | -- | -- | -- | -- |
| 10 | -- | -- |
WX
YZ
1
1
1
1
1
1
1
1
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
+
+
+
+
+
+
+
A=
!WXY!Z
!WXYZ
!W!XY!Z
!W!XYZ
!W!XY
!W!XY
!WXY
!WXY
!WY
!WY
Our Seven Segment Display
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | -- | -- | -- | -- |
| 10 | -- | -- |
WX
YZ
1
1
1
1
1
1
1
1
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
+
+
+
+
+
+
+
A=
!WXY!Z
!WXYZ
!W!XY!Z
!W!XYZ
!W!XY
!W!XY
!WXY
!WXY
!WY
!WY
Our Seven Segment Display
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | ||||
| 11 | -- | -- | -- | -- |
| 10 | -- | -- |
WX
YZ
1
1
1
1
1
1
1
1
!W!X!Y!Z
W!X!YZ
W!X!Y!Z
!WXY!Z
!WXYZ
!WX!YZ
!W!XY!Z
!W!XYZ
+
+
+
+
+
+
+
A=
!W!XY
!W!XY
!WXY
!WXY
!WY
!WY
=!W!XY
=!WXY
!W!XY!Z
!W!XYZ
+
!WXY!Z
!WXYZ
+
WHAT WE'D LIKE
A dependable method for simplifying any logical expression
Logic Reduction
AB + A!B = A(B+!B) = A and TRUE = A
A may be a compound expression:
PQR + PQ!R = (PQ)(R+!R) = PQ
P=ABCD + ABC!D + AB!C + A!B
ABC(D+!D)
ABC
AB(C+!C)
AB
A(B+!B)
A
change A
ABCD
A!BCD
ABC!D
AB!CD
!ABCD
change C
change B
change D
A B C D Y 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 0 0 1 0 0 1 0 1 0 0 0 0 0 1 1 1 1 0 1 1 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 1 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0
AB
CD
ABCD
ABC!D
AB!CD
AB!C!D
A!BCD
!ABCD
!A!BCD
ABC
AB!C
ACD
!ACD
| CD | |||||
|---|---|---|---|---|---|
| 00 | 01 | 11 | 10 | ||
| AB |
00 |
!A!B!C!D |
!A!B!CD |
!A!BCD |
!A!BC!D |
|
01 |
!AB!C!D |
!AB!CD |
!ABCD |
!ABC!D |
|
|
11 |
AB!C!D |
AB!CD |
ABCD |
ABC!D |
|
|
10 |
A!B!C!D |
A!B!CD |
A!BCD |
A!BC!D |
|
Karnaugh Map
| CD | |||||
|---|---|---|---|---|---|
| 00 | 01 | 11 | 10 | ||
| AB | 00 | !A!B!C!D 0 |
!A!B!CD1 | !A!BCD 3 |
!A!BC!D 2 |
| 01 | !AB!C!D 4 |
!AB!CD 5 |
!ABCD 7 |
!ABC!D 6 |
|
| 11 | AB!C!D 12 |
AB!CD 13 |
ABCD 15 |
ABC!D 14 |
|
| 10 | A!B!C!D 8 |
A!B!CD 9 |
A!BCD 11 |
A!BC!D 10 |
|
Karnaugh Map
| CD | |||||
|---|---|---|---|---|---|
| 00 | 01 | 11 | 10 | ||
| AB | 00 |
|
|
|
|
| 01 |
|
|
|
|
|
| 11 | AB!C!D 1 |
AB!CD 1 |
ABCD 1 |
ABC!D 1 |
|
| 10 | A!B!C!D 1 |
A!B!CD 1 |
A!BCD 1 |
A!BC!D 1 |
|
P=ABCD + ABC!D + AB!CD + A!BCD + AB!C!D +A!B!CD + A!B!C!D + A!BC!D
| CD | |||||
|---|---|---|---|---|---|
| 00 | 01 | 11 | 10 | ||
| AB | 00 |
|
|
|
|
| 01 |
|
|
|
|
|
| 11 | AB!C!D 1 |
AB!CD 1 |
ABCD 1 |
ABC!D 1 |
|
| 10 | A!B!C!D 1 |
A!B!CD 1 |
A!BCD 1 |
A!BC!D 1 |
|
P=ABCD + ABC!D + AB!CD + A!BCD + AB!C!D +A!B!CD + A!B!C!D + A!BC!D
| CD | |||||
|---|---|---|---|---|---|
| 00 | 01 | 11 | 10 | ||
| AB | 00 |
|
|
|
|
| 01 |
|
|
|
|
|
| 11 | AB!C!D 1 |
AB!CD 1 |
ABCD 1 |
ABC!D 1 |
|
| 10 | A!B!C!D 1 |
A!B!CD 1 |
A!BCD 1 |
A!BC!D 1 |
|
P=ABCD + ABC!D + AB!CD + A!BCD + AB!C!D +A!B!CD + A!B!C!D + A!BC!D
| CD | |||||
|---|---|---|---|---|---|
| 00 | 01 | 11 | 10 | ||
| AB | 00 |
|
|
|
|
| 01 |
|
|
|
|
|
|
11 |
1 | 1 | 1 | 1 | |
|
10 |
1 | 1 | 1 | 1 | |
P=ABCD + ABC!D + AB!C + A!B
P=ABCD + ABC!D + AB!CD + AB!C!D + A!BCD + A!BC!D + A!B!CD + A!B!C!D
Finis
NOTE: X1=B, X3=A, X0=C, X2=D
C is 1 here
D is 1 here
A is 1 here
B is 1 here
KMaps & Race Conditions
A


C
B
D
1 0 1 1 1 0 1
R=!ABC!D+A!B!C!D+A!B!CD+A!BC!D+A!BCD+AB!C!D+AB!CD+ABC~D
| 00 | 01 | 11 | 10 | |
| 00 | ||||
| 01 | 1 | |||
| 11 | 1 | 1 | 1 | |
| 10 | 1 | 1 | 1 | 1 |
AB
CD
A!C




A!B
R=A!B + A!C + BC!D
BC!D
1 0 1 1 1 0 0
0 0 1 1 0 0 0
0 0 1 1 1 0 1
1 1 1 1 1 1
Race Conditions - the race is among these AND gates. Their inputs depend on A, B, C, and D but some might be delayed by NOT
0 1 0 0
!A
0 1 0 0
!B
0 0 0 0
!C
1 1 1 0
!D
1 1 1 1
A
1 0 1 1
B
1 1 1 1
C
0 0 0 0
D

R=A!B + A!C + BC!D
R=A!B + A!C + BC!D + A!D