Math of Causal Inference
Fall 2022
N individuals indexed by i=1,...,N
Wi indicates whether or not individual i receives treatment
Wi = 1 if yes, 0 if no
W is an N-vector with the ith element equal to Wi
For each individual we also observe K other characteristics
or "pre-treatment variables"
or "covariates"
This means we have an N x K matrix of covariates.
We call it X
For each individual, i, there are two possible outcomes:
Yi(0) = what individual i would experience without treatment
Yi(1) = what individual i would experience with treatment
Translate this line of math into ordinary language
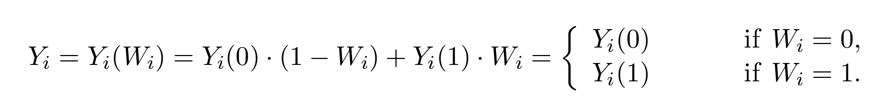
depends on treatment individual i receives
The outcome individual i actually experiences
This term disappears if Wi is 1
This term disappears if Wi is 0
This bracket notation with two lines means the top left value if the top right condition holds, and the bottom left value if the bottom right condition holds.
Translate this line of math into ordinary language. Take it one term at a time
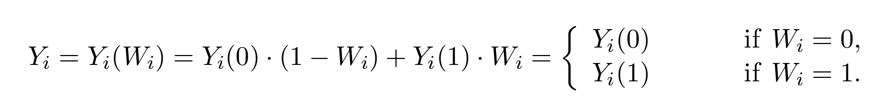
Translate these assertions about the assignment mechanisms for randomized experiments
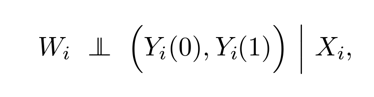
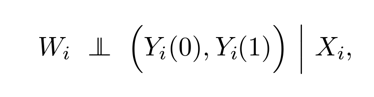
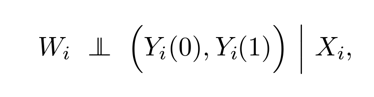
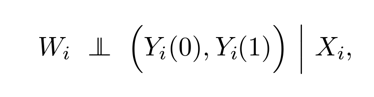
= "is independent of"
= "given that" or "conditional on"
The probability that any given individual is assigned to treatment or control is independent of potential outcomes.
The probability that any given individual is assigned to treatment or control is independent of potential outcomes and is a known function of covariates (for example, we might decide to have more women than men in our treatment group).
Translate these assertions about the assignment mechanisms for randomized experiments
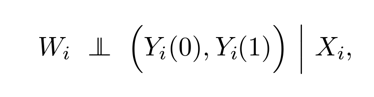
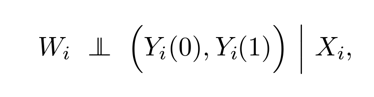
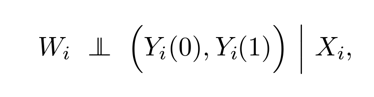
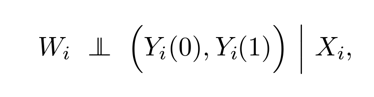
= "is independent of"
= "given that" or "conditional on"
How would you read each of the expressions in this image from one of the first readings of the semester?
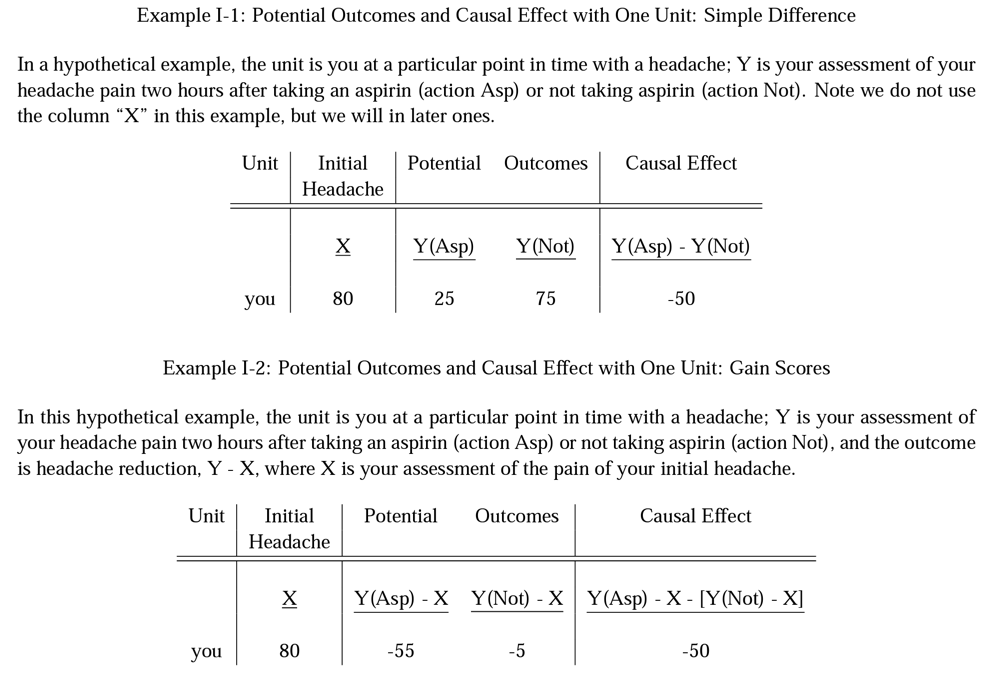
Y(Asp) is how my head feels two hours after taking an aspirin. Y(Not) is how my head feels two hours after not taking an aspirin.
The causal effect is the difference between how I feel two hours after taking an aspirin and two hours after not taking an aspirin.
The outcome is how my head feels two hours after taking an aspirin as compared to how it felt before I took the aspirin.
The causal effect is the difference between the change in my headache after an aspirin and the change in my headache after no aspirin.
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 4
How would you read each of the expressions in this image from one of the first readings of the semester? Write a sentence or two.
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 4
This table represents an experiment in which you and I both have headaches. Explain what the selected part of the table means.
The column Asp Not corresponds to you taking an aspirin and me not taking an aspirin.
The subscripts 1 and 2 refer to your and my, respectively, outcomes - how our heads feel at the end of two hours.
In the square brackets we have the treatments - you took an aspirin and I did not.
The numbers indicate the "value" of each of our headaches.
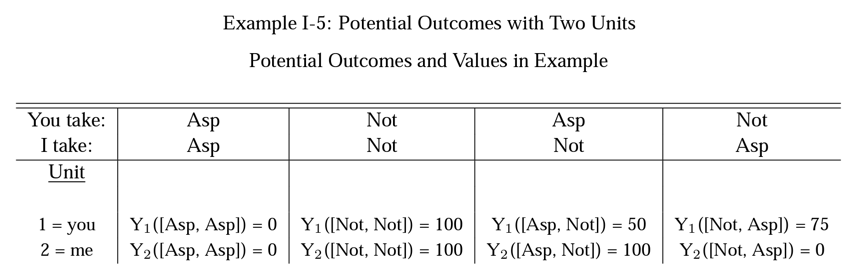
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 6
This table represents an experiment in which you and I both have headaches. Explain what the selected part of the table means.
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 6
This table represents an experiment in which you and I both have headaches. How does the information in the green box indicate that SUTVA is violated?
The treatment effect for you when I take an aspirin is = Y1([Asp,Asp]) - Y1([Not,Asp]) = 0 - 75 = -75
But the treatment effect for you when I do not take an aspirin is
= Y1([Asp,Not]) - Y1([Not,Not]) = 50 - 100 = -50
The causal effect for you depends in some way on whether I get treatment or control. That violates first part of SUTVA.
Make up a story that might explain this peculiar situation.
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 6
This table represents an experiment in which you and I both have headaches. How does the information in the green box indicate that SUTVA is violated?
Make up a story that might explain this peculiar situation.
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 6
Here are four ways one might formulate POPULATION level causal effects in the "aspirin/headache" study. Explain what each says in ordinary language.
1.The average headache two hours after an aspirin minus the average headache two hours after not taking an aspirin.
Avg[Yi(Asp)-Yi(Not)]
Avg[Yi(Asp)]-Avg[Yi(Not)]
Med[Yi(Asp)-Yi(Not)]
Med[Yi(Asp)]-Med[Yi(Not)]
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 7
4. The difference between the median headache two hours after an aspirin and the median headache two hours after not taking an aspirin.
2. The average of the difference each unit experiences between taking and not taking an aspirin.
3. The median difference between how people felt when they did and did not take an aspirin.
Here are four ways one might formulate POPULATION level causal effects in the "aspirin/headache" study. Explain what each says in ordinary language.
Avg[Yi(Asp)-Yi(Not)]
Avg[Yi(Asp)]-Avg[Yi(Not)]
Med[Yi(Asp)-Yi(Not)]
Med[Yi(Asp)]-Med[Yi(Not)]
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 7
Read this definition of a propensity score in ordinary language.
Propensity Score: For a unit with covariates X=x, the probability of being assigned treatment:
PS(x) = prob(T = 1|X=x)
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 18
- What do each of the underlined parts of this mathematical description of an assignment mechanism mean?
- What does it mean altogether?
pr(X|a,b,c) = pr(X|a)
Read this definition of a propensity score in ordinary language.
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 18
pr(X|a,b,c) = pr(X|a)
probability of being in treatment group
given unit i's characteristics
and what would happen under treatment and no treatment
is the same as
pr(T) given i's characteristics and the observed outcome
means the probability of X given a, b, and c is the same as the probability of X given a.
pr(X|a,b,c) = pr(X|a)
And that means the X does not depend on b, and c.
- What do each of the underlined parts of this mathematical description of an assignment mechanism mean?
- What does it mean altogether?
Read this definition of a propensity score in ordinary language.
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin. P 18
means the probability of X given a, b, and c is the same as the probability of X given a.
pr(X|a,b,c) = pr(X|a)
And that means the X does not depend on b, and c.
probability of being in treatment group
given unit i's characteristics
and what would happen under treatment and no treatment
is the same as
pr(T) given i's characteristics
simplified notation.pdf - 1
simplified notation.pdf - 2
What is: E [ Y | D = 1] ?
Is it observable?
The expected value of the outcome Y given that treatment 1 was received. If some of the units received treatment 0 then we cannot observe this.
simplified notation.pdf - 2
What is: E [ Y | D = 1] ?
Is it observable?
The expected value of the outcome Y given that treatment 1 was received. If some of the units received treatment 0 then we cannot observe this.
simplified notation.pdf - 3
What is: E [ Y1 ] ?
Is it observable?
The expected value of the outcome Y given that treatment 1 was received. If some of the units received treatment 0 then we cannot observe this.
simplified notation.pdf - 3
What is: E [ Y1 ] ?
Is it observable?
The expected value of the outcome Y given that treatment 1 was received. If some of the units received treatment 0 then we cannot observe this.
simplified notation.pdf - 4
What is: E [ Y | D = 0]?
Is it observable?
The expected value of the outcome Y given that treatment 0 was received. If some of the units received treatment 1 then we cannot observe this.
simplified notation.pdf - 4
What is: E [ Y | D = 0]?
Is it observable?
The expected value of the outcome Y given that treatment 0 was received. If some of the units received treatment 1 then we cannot observe this.
simplified notation.pdf - 5
What is: E [ Y0 ] ?
Is it observable?
The expected value of the outcome Y given that treatment 0 was received. If some of the units received treatment 1 then we cannot observe this.
simplified notation.pdf - 5
What is: E [ Y0 ] ?
Is it observable?
The expected value of the outcome Y given that treatment 0 was received. If some of the units received treatment 1 then we cannot observe this.
ICS212 Fall 2022
simplified notation.pdf - 6
RECAP:
E [ Y0 ] E [ Y1 ] E [ Y | D = 0] E [ Y | D = 1]
simplified notation.pdf - 7
What is: E [ Y | D = 1] - E [ Y | D = 0] ?
Is it observable?
The expected value of the Y given that treatment 1 was received minus the expected value of the outcome given that treatment 0 was received. This is the true treatment effect. It is not observable.
simplified notation.pdf - 7
What is: E [ Y | D = 1] - E [ Y | D = 0] ?
Is it observable?
The expected value of the Y given that treatment 1 was received minus the expected value of the outcome given that treatment 0 was received. This is the true treatment effect. It is not observable.
ICS212 Fall 2022
simplified notation.pdf - 8
What is: E [ Y0 | D = 0]?
Is it observable?
The expected value of the outcome Y after treatment 0 given that treatment 0 was received. These are the control group cases and they can be observed.
simplified notation.pdf - 8
What is: E [ Y0 | D = 0]?
Is it observable?
The expected value of the outcome Y after treatment 0 given that treatment 0 was received. These are the control group cases and they can be observed.
ICS212 Fall 2022
simplified notation.pdf - 9
What is: E [ Y1 | D = 1]?
Is it observable?
The expected value of the outcome Y after treatment 1 given that treatment 1 was received. These are the treatment group cases and they can be observed.
simplified notation.pdf - 9
What is: E [ Y1 | D = 1]?
Is it observable?
The expected value of the outcome Y after treatment 1 given that treatment 1 was received. These are the treatment group cases and they can be observed.
ICS212 Fall 2022
simplified notation.pdf - 10
What is: E [ Y0 | D = 1]?
Is it observable?
The expected value of the outcome Y after treatment 0 given that treatment 1 was received. These are imaginary cases and they cannot be observed.
simplified notation.pdf - 10
What is: E [ Y0 | D = 1]?
Is it observable?
The expected value of the outcome Y after treatment 0 given that treatment 1 was received. These are imaginary cases and they cannot be observed.
ICS212 Fall 2022
simplified notation.pdf - 11
What is: E [ Y1 | D = 0]?
Is it observable?
The expected value of the outcome Y after treatment 1 given that treatment 0 was received. These are imaginary cases and they cannot be observed.
simplified notation.pdf - 11
What is: E [ Y1 | D = 0]?
Is it observable?
The expected value of the outcome Y after treatment 1 given that treatment 0 was received. These are imaginary cases and they cannot be observed.
ICS212 Fall 2022
simplified notation.pdf - 12
What is: E [ Y0 | D = 1] - E [ Y0 | D = 0]?
Is it observable?
The difference between the expected outcome for the treatment group had they not been treated and the expected outcomes of the control group. This is not observable
simplified notation.pdf - 12
What is: E [ Y0 | D = 1] - E [ Y0 | D = 0]?
Is it observable?
The difference between the expected outcome for the treatment group had they not been treated and the expected outcomes of the control group. This is not observable
ICS212 Fall 2022
In this example "S/s" refers to "getting the surgery" and "N/n" refers to choosing not to get the surgery. The outcome Y is how healthy individuals are after getting or not getting the surgery. Annotate each numbered step.
NCE = E(Ys|S) - E(Yn|N)
NCE = E(Ys|S) - E(Yn|N) + E(Yn|S) - E(Yn|S)
Add and subtract E(Yn|S) - E(Yn|S)
NCE = E(Ys|S) - E(Yn|S) - E(Yn|N) + E(Yn|S)
NCE = [E(Ys|S) - E(Yn|S)] - [E(Yn|S) - E(Yn|N)]
ATT
Selection Bias
ATT = NCE - SB
Naive Causal Effect = NCE
ATT = [E(Y1|D=1)-E(Y0|D=0)] - [E(Y0|D=1)-E(Y0|D=0)]
In our previous notation
1
2
3
4
5
6
If selection bias is given by these equations:
SB = E(Yn|S) - E(Yn|N)
SB = E(Y0|D=1) - E(Y0|D=0)
Explain in ordinary language what's being subtracted from what and why the difference means something important here.
If selection bias is given by these equations:
SB = E(Yn|S) - E(Yn|N)
ATT = NCE - SB
SB = E(Y0|D=1) - E(Y0|D=0)
Describe in ordinary language what happens when HEALTHIER patients choose to have the surgery.
Describe in ordinary language what happens when SICKER patients choose to have the surgery.
material on the stochastic and systematic
Here are four ways one might formulate POPULATION level causal effects. Explain what each says in ordinary language.
aasdfg
Make up a story that might explain this peculiar situation.
Theunitlevel causal effects cannot be observed; remember the fundamental problem of causal inference. That means that population level causal effects also cannot be observed, even under SUTVA. • To learn about causal effects, we must have replication. In the example above, we require some units with Yi(Asp) observed and some with Yi(Not) observed. • Theassignment mechanism determines how to choose which potential outcome we will observe for each unit. Formally, the assignment mechanism is a probabilistic or deterministic rule for selecting some units to receive control and other units to receive treatment. It describes what we do (or what was done) to learn about the science: X, Y(1), Y(0). • Theassignment mechanism is critical, even if SUTVA holds. We must know or posit a rule for how each unit received treatment or control.
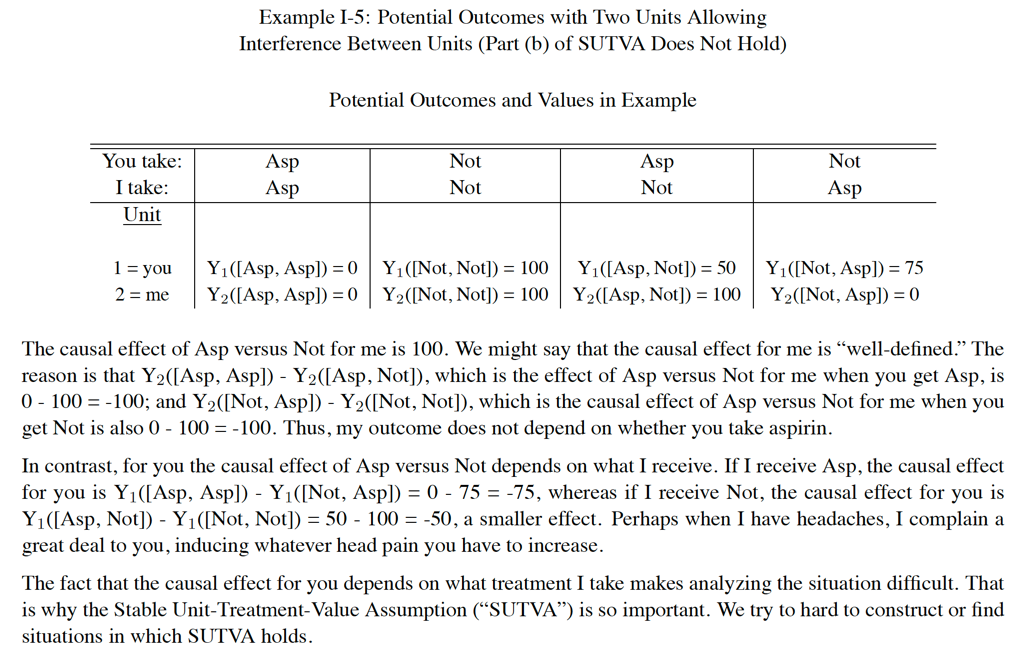
Basic Concepts of Statistical Inference for Causal Effects in Experiments and Observational Studies Donald B. Rubin p 6