Repetition

What to learn: Reflexes and Repertoire
1. “I wonder if problem can be solved by repetition….”
-
Repertoire
-
Reflexes
3. Big O
3. How big is this problem?
2. Is big problem actually a set of small problems?
2. Recursion
1. loops and nested loops
4. Backtracking, heuristics, divide and conquer, dynamic programming, branch/bound


How Do We Get From
THIS
TO
THIS

STOP+THINK
Why do we think this works?
Practice
Ich habe eine Geige.
Ich habe einen Freund.
Ich habe eine Garage.
Ich habe ein Fahrrad.
Ich habe einen Hund.
Ich habe eine Idee.
Tutorial


STOP+THINK
How
does nature
do this?

Dissecting Repetition
Filho Ch 3 "Strategy"

Iteration
Nested Loops
Power Set
Recursion
Brute Force
Back Tracking
Heuristics
Greedy Approaches
Divide and Conqueur
Dynamic Programming (memoizing)
Branch and Bound
O(n), O(nlogn), O(n2), O(2n)
Merge (four players)
player D is the "accountant"
players A and B each have pile of ordered cards
repeat
if both A and B have a card
Player C examines top of each pile; takes smaller one
otherwise
if player A has a card
take it
otherwise
take card from B
notify the accountant that one operation has taken place
until neither A nor B has cards left
Accountant reports: #operations, total # cards
Bubble Sort (two players)
Player A has a hand of cards. Mix them up.
Player B is the accountant.
Spread them out in a single line, left to right on the table.
repeat
start from left-most card
for all but the last unsorted card
compare card and it's right neighbor
tell the accountant that a comparison happened
if card higher than neighbor
switch cards
tell the accountant that a switch happened
declare the last card to be sorted
until just one card unsorted
Accountant reports: #compares, #switches, total # cards
Power Set
- Appoint an accountant
- List the "ingredients" for your power set.
- Take a blank sheet, landscape orientation, and divide into a left half and a right half.
- Put one empty sticky note on the left side
- Iterate over your set of ingredients
- For each sticky on the left make a copy and put it on the right
- Add the current ingredient to each sticky on the right
- Tell the accountant we did one operation
- move all the stickies on the right to the left
Power Set
for the set of ingredients: orange, yellow, blue
COPY
Start with an empty set
Create a
orange
Power Set
for the set of ingredients: orange, yellow, blue
Create a
Add orange
orange
Power Set
for the set of ingredients: orange, yellow, blue
Create a
RETURN
orange
Power Set
for the set of ingredients: orange, yellow, blue
Create a
COPY
orange
orange
orange
yellow
yellow
Power Set
for the set of ingredients: orange, yellow, blue
Create a
Add yellow
orange
orange
yellow
yellow
Power Set
for the set of ingredients: orange, yellow, blue
Create a
RETURN
orange
orange
yellow
yellow
Power Set
for the set of ingredients: orange, yellow, blue
Create a
COPY
yellow
orange
yellow
orange
orange
orange
yellow
yellow
orange
orange
yellow
yellow
blue
blue
blue
blue
Power Set
for the set of ingredients: orange, yellow, blue
Create a
Add blue
orange
orange
yellow
yellow
orange
orange
yellow
yellow
blue
blue
blue
blue
Power Set
for the set of ingredients: orange, yellow, blue
Create a
RETURN
orange
orange
yellow
yellow
orange
orange
yellow
yellow
blue
blue
blue
blue
Power Set
for the set of ingredients: orange, yellow, blue
Create a
3 elements
23 = 8 elements
Merge Sort (whole class)
Appoint an accountant
All participants run this code:
receive cards
if more than one card
divide in half
pass each half to another player
report "split" to accountant
wait for cards to be returned
merge returned cards into single pile
report number of merge steps to accountant
return card(s) to sender
Hand deck of cards to one player
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
3
5
6
7
8
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
5
10
4
6
7
8
9
1
2
5
3
10
7
8
4
6
9
1
2
4
9
3
5
6
7
8
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
5
10
4
6
7
8
9
1
2
5
3
10
7
8
4
6
9
1
2
4
9
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10





















# merges depends on log2 N
O(N log2 N)
number of objects/cases/datapoints
time
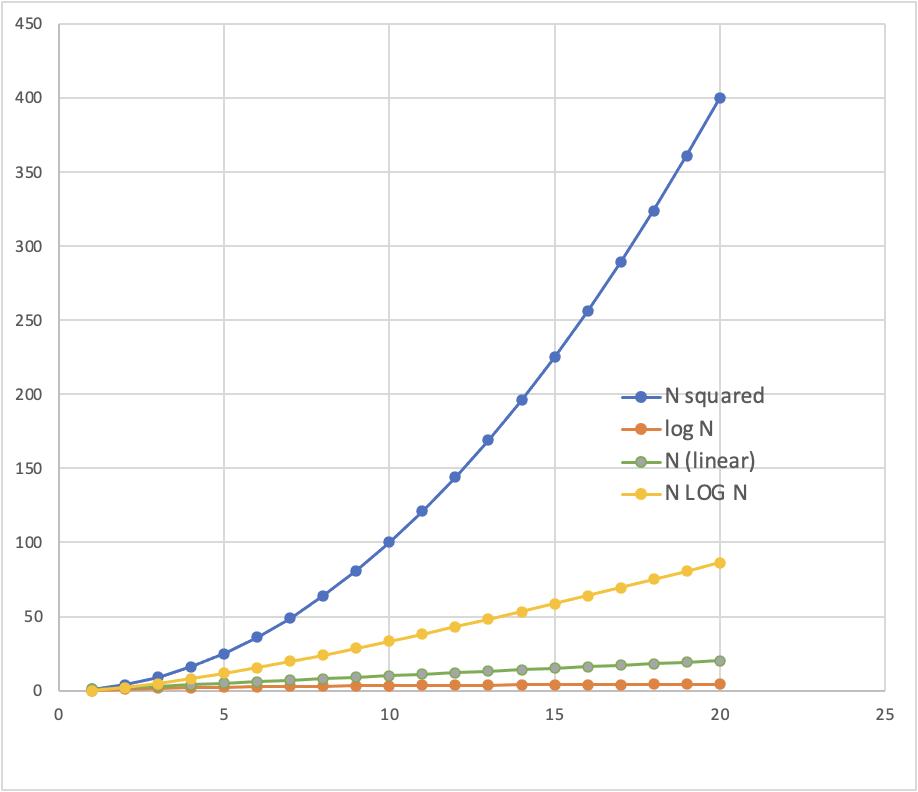
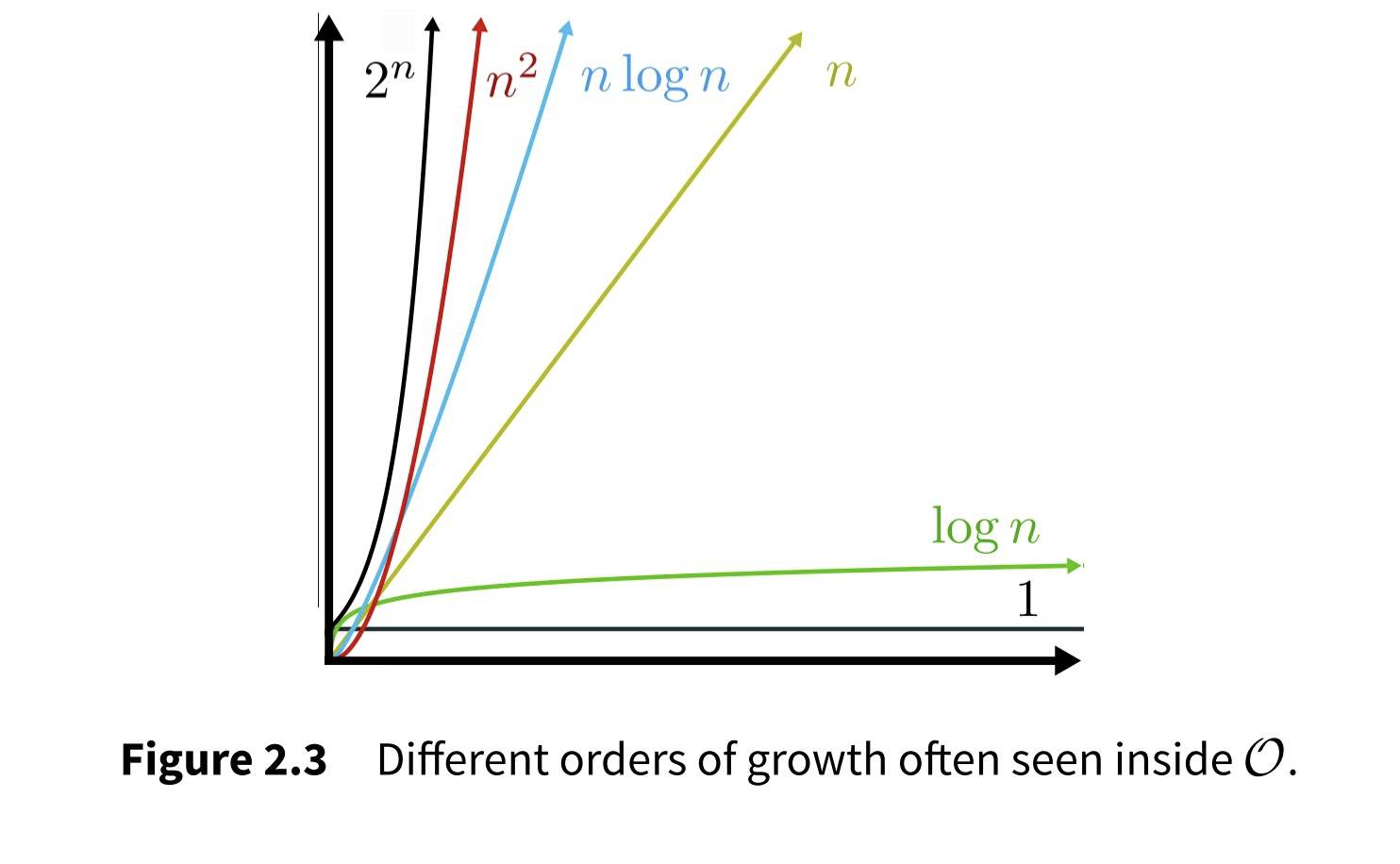
"constant" time
"linear" time
"exponential" time
"quadratic" time
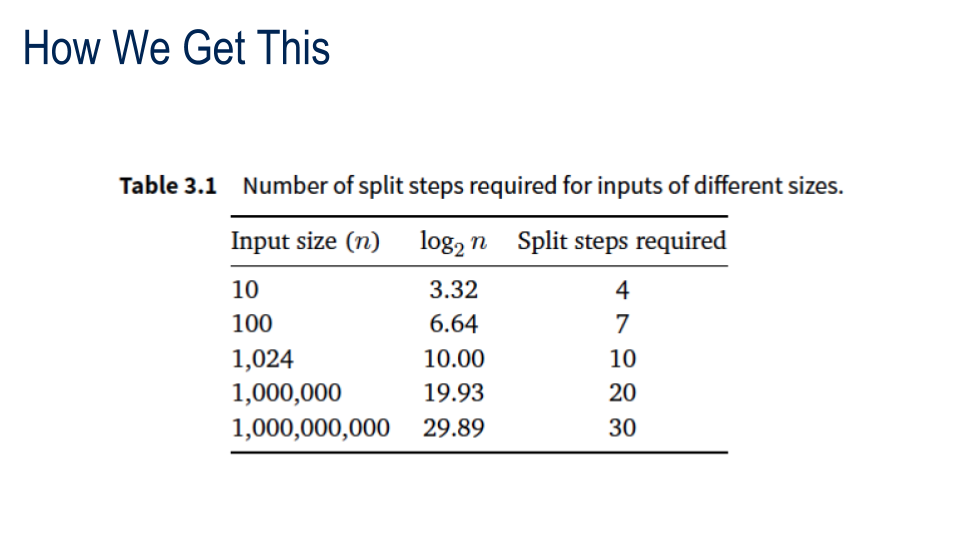
Find a Word in a Dictionary with N words
Find a Word in a Dictionary with N words
STOP+THINK: For how long can this go on?
N > N/2 > N/4 > N/8 > ... 1 and DONE
Think powers of 2 - the number of steps is the power of two that's closest to N.
This reminds us of binary numbers: the number of splits is the number of binary digits needed to represent N
Introducing Logarithms

Introducing Logarithms
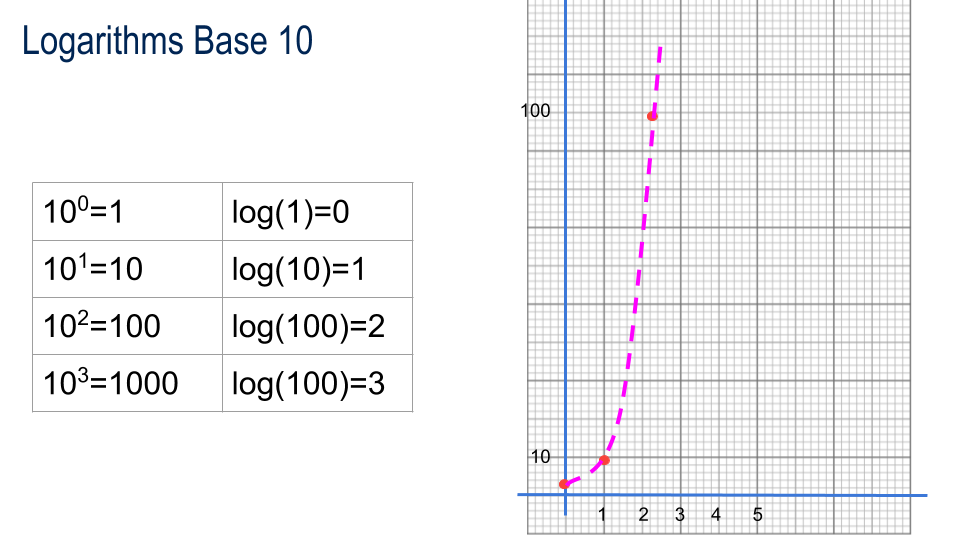
| 100=1 | log(1)=0 |
| 101=10 | log(10)=1 |
| 102=100 | log(100)=2 |
| 103=1000 | log(1000)=3 |
logarithms base 10
Introducing Logarithms

Introducing Logarithms
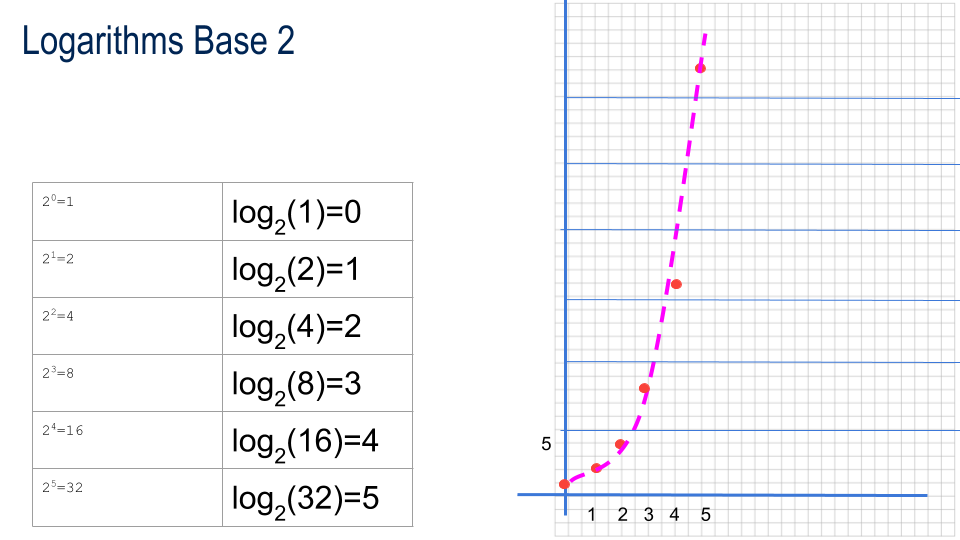
| 20=1 | log(1)=0 |
| 21=2 | log(2)=1 |
| 22=4 | log(4)=2 |
| 23=8 | log(8)=3 |
logarithms base 2
Find a Word in a Dictionary with n pages
STOP+THINK: For how long can this go on?
Fibonacci (whole class)
One student appointed accountant
Every student in the class is "programmed" as follows:
When you are asked for F(n)
put up a sign that says "busy"
if n is 2 or 1 just say 1
Otherwise
find two other students who are not busy
ask first for F(n-1) and second for F(n-2)
Accountant tallies an "ask"
Wait for answers.
When you get them
add together
say result to the person who asked you.
Roll 2 dice to get a number, n, we want the Fibonacci of
Instructor says to student 1 : "What is Fibonacci(n)?"
Fibonacci with Memo (whole class)
One student appointed "Memo-izer"
One student appointed accountant
Every student in the class is "programmed" as follows:
When you are asked for F(n)
ask memoizer if F(n) is known; if so, respond with it and done
put up a sign that says "busy"
if n is 2 or 1 just say 1
Otherwise
find two other students who are not busy
ask first for F(n-1) and second for F(n-2)
Wait for answers.
When you get them
add together
tell memoizer result to write down
say result to the person who asked you.
Palindrome Game (whole class)
Student A thinks of a word Student B says "is the word longer than 1 letter?" If NO say "IT'S A PALINDROME!!!" STOP Else "remove first and last letters and tell me what they are" if not the same say "IT'S NOT A PALINDROME!" STOP REPEAT
Queens (pairs)
Draw 8x8 board column 1, row 1 Repeat if current square is "safe" place queen otherwise next in this column until column exhausted backtrack
DRAFT
solveQueens(board)
if numberQueens = 8
return board //success!
try each un-attacked position
place queen in position
solution = solve board from there
if we get a solution
we're done
otherwise remove queen
return false
Knapsack - Greedy (pairs)
note max allowable weight initial weight 0 empty bag sort all items by value iterate over items is there room in the bag for this item? yes, add it
Traveling Salesperson - Greedy
if this is a map of cities in Romania, let's visit them all via a greedy algorithm
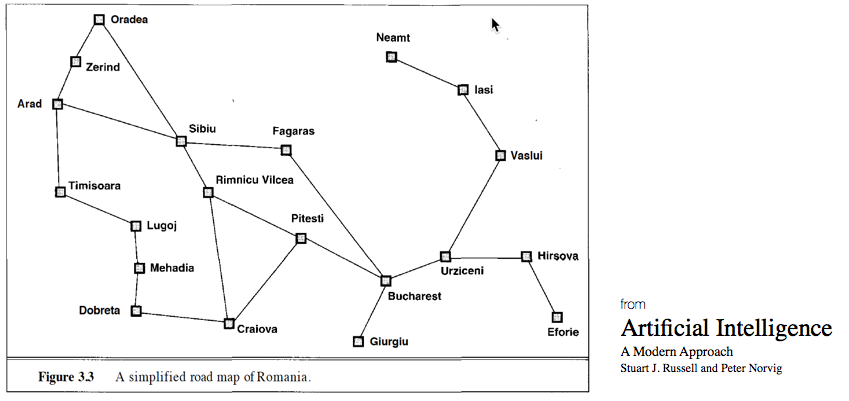
Optimization Problem
Branch and Bound
Solutions that involve backtracking might be improved if we could avoid "bad" choices to begin with.
What we have:
Colors
#002554
#FED141
#007396
#007396
#382F2D
#3EB1C8
#F9423A
