Electrostatics

The Electric Potential

 Electrostatics

      The Electric Potential

           Learning Outcomes

Learn how to:

Calculate the electric potential at a given point in space due to

  • a configuration of point charges.
  • a "continuous" distribution of electric charges.

Relate the electric potential to

  • the electric potential energy
  • the electric field

 Electrostatics

      The Electric Potential

           Walkthrough

Electrostatics

The Electric Charge

Charge Distribution

 Electrostatics

      Electric Charge

           Charge Distributions

\lambda = dq / dl

Linear Charge Density

\sigma=dq / dA

Surface Charge Density

\rho=dq / dV

Volume Charge Density

\lambda_\text{\tiny uniform} = \frac{Q_\text{\tiny total}}{l_\text{\tiny total}}
\sigma\text{\tiny uniform} = \frac{Q_\text{\tiny total}}{A_\text{\tiny total}}
\rho\text{\tiny uniform} = \frac{Q_\text{\tiny total}}{V_\text{\tiny total}}

 Electrostatics

      Electric Charge

           Point Charge

Charge distribution A

Charge distribution B

What do we mean by point charges?

\text{size$_\text{charge distribution}$}
\text{scale of analysis}
\lt\lt\lt

Electrostatics

The Electric Charge

... and the rest of the cast

 Electrostatics

      The influence & interaction of electric charges

           The Cast 

q
\vec{E}
V
\Phi
\vec{F}
U

potential

potential energy

field

force

charge

flux

influence

interaction

Electric ....

 Electrostatics

      The influence & interaction of electric charges

           The Cast - relationship map

Electric ....

\vec{E}
V
\Phi

influence

interaction

\ \vec{E}=-\vec{\nabla} V\
\ \Delta V = -\int \vec{E}\cdot d\vec{s}\
\ \Phi = \int \vec{E}\cdot d\vec{A}\
\vec{F}
U
\ \vec{F}=-\vec{\nabla} U\
\ \Delta U = -\int \vec{F}\cdot d\vec{s}\
\ \vec{F} = q_0\ \vec{E}\
\ \vec{E} = \vec{F}/q_0\ \
\ U = q_0\ V\
\ V = U/q_0\ \
q

 Electrostatics

      The influence & interaction of electric charges

           The Cast - relationship map

Electric ....

\vec{E}
V
\Phi

influence

interaction

\ \vec{E}=-\vec{\nabla} V\
\ \Delta V = -\int \vec{E}\cdot d\vec{s}\
\ \Phi = \int \vec{E}\cdot d\vec{A}\
\vec{F}
U
\ \vec{F}=-\vec{\nabla} U\
\ \Delta U = -\int \vec{F}\cdot d\vec{s}\
\ \vec{F} = q_0\ \vec{E}\
\ \vec{E} = \vec{F}/q_0\ \
\ U = q_0\ V\quad
\ V = U/q_0\ \
q
\Phi_g

influence

\ \Phi_g = \int \vec{g}\cdot d\vec{A}\
\vec{g}
gy
\ \vec{g}=-\vec{\nabla} (gy)\
\ \Delta V = \int \vec{g}\cdot d\vec{s}\
\vec{F}_g
mgy

interaction

\ \vec{F}=-\vec{\nabla} (mgy)\\ =-mg\hat j
\ \Delta U = -\int \vec{F}\cdot d\vec{s}\
m
\ \vec{F_g} = m\ \vec{g}\
\ \vec{g} = \vec{F_g}/m\ \
\ U_g = m\ V_g\
\ V_g = U_g/m\ \

gravitational....

analogus to

Electrostatics

The Electric Potential

conceptual overview

Electrostatics

The Electric Potential

conceptual overview

Follow along with [CQ] Electric Potential

 Electrostatics

      The Electric Potential

           Conceptual overview

Electric Charges have an influence in their vicinity that we call the Electric Potential.

Perhaps you can think of it as a fictious glow surrounding each charge.

The "glow" at any point in space is the combined result of all the "glow" from the distribution of charges.

 Electrostatics

      The Electric Potential

           Conceptual overview

The Electric Potential due to a point charge is proportional to the charge.

The Electric Potential due to a point charge is ...

inversely    proportional to the distance from that charge.

The Electric Potential at some location due to a point electric charge depends on the material(s) in the region(s) separating the charge and that location.

 Electrostatics

      The Electric Potential

           Conceptual overview

The Electric Potential due to a point charge is    

V(r)=\frac{kq}{r}

given by ...

charge creating potential.

distance from the charge q to the point of interest P

material-dependent proportionality constant

k:
q:
r:

 Electrostatics

      The Electric Potential

           Point-charge

V(r)=\frac{kq}{r}
\text{the Electric Potential due to a point-charge $q$ at some distance $r$}

Visualizingthe Electric Potential from a point-charge

Electrostatics

The Electric Potential

due to a point charge

 Electrostatics

      The Electric Potential

           Point-charge

Video walkthrough this stack

 Electrostatics

      The Electric Potential

           Point-charge

V(r)=\tfrac{1}{4\pi\epsilon}\frac{q}{r}
\text{the Electric Potential due to a point-charge $q$ at some distance $r$}
\text{permittivity}
\text{SI unit: Volt (V)}
\text{Volt}= \text{Joule / Coulomb}
\text{Scalar Quantity } (\pm)
\kappa : \text{relative permittivity (Dielectric Constant)}
\text{Permittivity of free space: } \epsilon_0=8.854\times10^{-12}\ C^2/Nm^2
\text{Absolute Permittivity (material dependent): } \epsilon = \kappa \epsilon_0
\text{In free space: } k=1/4\pi\epsilon_0 = 8.99\times10^{9}\ Nm^2/C^2

 Electrostatics

      The Electric Potential

           Point-charge

V(r)=\tfrac{1}{4\pi\epsilon_0}\frac{q}{r}
\text{**Calculate the electric potential produced by}\\\text{ a point-charge of $3.0\mu C$ at a distance of 2.0mm}
=\tfrac{(8.99\times10^9 Nm^2/C^2) \ \times (3\times10^{-6} \ C)}{(2 \times10^{-3} m)}
=1.3\times10^7 V

 Electrostatics

      The Electric Potential

           Point-charge

V(r)=\tfrac{1}{4\pi\epsilon_0}\frac{q}{r}
\text{**Calculate the electric potential produced by}\\\text{ a point-charge of $3.0\mu C$ at a distance of 2.0mm}
=\tfrac{(8.99\times10^9 Nm^2/C^2) \ \times (3\times10^{-6} \ C)}{(2 \times10^{-3} m)}
=1.3\times10^7 V

 Electrostatics

      The Electric Potential

           Point-charge

V=\tfrac{1}{4\pi\epsilon_0}\frac{q}{r}

Suppose that a point charge of 8.0nC is located at r_q=(0.50m, 1.5m) according to some 2D Cartesian coordinate system.
Calculate the electric potential produced by the charge at the shown locations P_1 and P_2.

x
y
0.50 m
=\tfrac{(8.99\times10^9 Nm^2/C^2) \ \times (8\times10^{-9} \ C)}{\sqrt{(6 \times0.5 m)^2+(2 \times0.5 m)^2})}
=23 V
=\tfrac{1}{4\pi\epsilon_0}\frac{q}{|\vec{r}_{P_1}-\vec{r_q}|}
P_1
P_2
=\tfrac{(8.99\times10^9 Nm^2/C^2) \ \times (8\times10^{-9} \ C)}{\sqrt{(2 \times0.5 m)^2+(-2 \times0.5 m)^2})}
=50 V
=\tfrac{1}{4\pi\epsilon_0}\frac{q}{|\vec{r}_{P_2}-\vec{r_q}|}

 Electrostatics

      The Electric Potential

           Point-charge

V(r)=\tfrac{1}{4\pi\epsilon}\frac{q}{r}

Example: 

In Bohr's model of the Hydrogen atom (1 proton + 1 electron), the electron orbits the proton in circular orbitals, whose radii are given by . Find an expression for the electric potential due to the proton at the location of the electron.and calculate for n=1. (known as the gorund state)

Electrostatics

The Electric Potential

due to a configuration of point charges

 Electrostatics

      The Electric Potential

           Multiple point charges

V_\text{@ P}={\Large \Sigma}_{\tiny {i=1}} ^{\tiny N} \ \frac{k\ q_i}{r_i}
\text{The Net Electric Potential due to multiple point-charges }
q_1
q_2
q_N
\text{algebriac sum}
\text{the contribution due to $q_i$}

 Electrostatics

      The Electric Potential

           Multiple point charges

V_\text{@ P}={\Large \Sigma}_{\tiny {i=1}} ^{\tiny N} \ \frac{k\ q_i}{r_i}

 Electrostatics

      The Electric Potential

           Multiple point charges

(a)
V_\text{@ P}={\Large \Sigma}_{\tiny {i=1}} ^{\tiny N} \ \frac{k\ q_i}{r_i}
=\frac{k\ (+q)}{2a} + \frac{k\ (-q)}{a}
=\frac{-kq}{2a}
(b)
V_\text{@ P}={\Large \Sigma}_{\tiny {i=1}} ^{\tiny N} \ \frac{k\ q_i}{r_i}
=\frac{k\ (+q)}{a} + \frac{k\ (+q)}{a}
=\frac{2kq}{a}

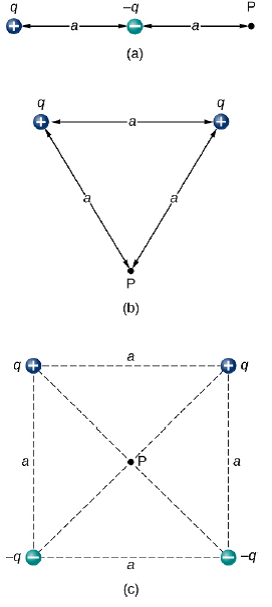
e.g. For each of the shown charge configurations, find an expression for the net Electric Potential at point P

(c)
V_\text{@ P}={\Large \Sigma}_{\tiny {i=1}} ^{\tiny N} \ \frac{k\ q_i}{r_i}
=\frac{k\ (+q)}{a/\sqrt{2}} + \frac{k\ (+q)}{a/\sqrt{2}}+\frac{k\ (-q)}{a/\sqrt{2}} + \frac{k\ (-q)}{a/\sqrt{2}}
=0

Electrostatics

The Electric Potential

Representation and Visualization

 Electrostatics

      The Electric Potential

           Visualizing the Electric Potential

Visualizing the Electric Potential from a point-charge -- phet

V_\text{@ P}={\Large \Sigma}_{\tiny {i=1}} ^{\tiny N} \ \frac{k\ q_i}{r_i}

 Electrostatics

      The Electric Potential

           Visualizing the Electric Potential

Visualizing the Electric Potential from a point-charge

V_\text{@ P}={\Large \Sigma}_{\tiny {i=1}} ^{\tiny N} \ \frac{k\ q_i}{r_i}

 Electrostatics

      The Electric Potential

Visualizingthe Electric Potential from a point-charge (1D)

V
x
y

           Visualizing the Electric Potential

V_\text{@ P}={\Large \Sigma}_{\tiny {i=1}} ^{\tiny N} \ \frac{k\ q_i}{r_i}

Electrostatics

The Electric Potential

Equipotential Surfaces

 Electrostatics

      The Electric Potential

           Equipotential Surfaces

The "landscape" analogy

 Electrostatics

      The Electric Potential

           Equipotential Surfaces

toggle between

3D view and  Equipotential view

Vary the charges and their locations

 Electrostatics

      The Electric Potential

           Equipotential Surfaces

In this simulation, the shown curves represent the intersection of the equipotential surfaces with the shown plan

use the pencil button on the cross-hairs tool.

 Electrostatics

      The Electric Potential

           Equipotential Surfaces

In this simulation, the shown curves represent the intersection of the equipotential surfaces with the chosen plan

show different slices to investigate the whole 3D space

 Electrostatics

      The Electric Potential

           Equipotential Surfaces

Mission:

  • Map the electric potential "landscape" and compare to expected
  • Investigate the average and local Electric Fields using the electric potential map.
  • ...

Part I: Map the electric potential "landscape"

  • Imagine an x-y coordinate system:
  • Place a charge +2nC at x=-1.500+/- 0.005m and y=0.000+/-0.005m
  • Place a charge -2nC at x=+1.500+/- 0.005m and y=0.000+/-0.005m

 Electrostatics

      The Electric Potential

           Equipotential Surfaces

Electrostatics

The Electric Potential

The Potential Difference (aka Voltage)

 Electrostatics

      The Electric Potential

            The Electric Potential Difference (aka Voltage)

\Delta V
\Delta V

ANALOG  VOLTMETER

The Instruments measure the electric potential difference between any two points in space.

 Electrostatics

      The Electric Potential

            The Electric Potential Difference (aka Voltage)

\Delta V
\Delta V

ANALOG  VOLTMETER

The Electric Potential is defined up to an arbitrary scalar shift

Therefore, it is the Electric Potential Difference that really matters

The Electric Potential Difference between any two points in space, A and B, is given by:

\Delta V= V_B-V_A

Electrostatics

The Electric Potential

and The Electric Potential Energy

 Electrostatics

      The Electric Potential

           Relationship to the Electric Potential Energy

Video Walkthrough this stack

 Electrostatics

V

influence at some location in space

interaction between charges

U
\ U = q_0\ V\
\ V = U/q_0\ \

      The Electric Potential

           Relationship to the Electric Potential Energy

Electric 

Potential

Electric 

Potential

Energy

 Electrostatics

      The Electric Potential

           Relationship to the Electric Potential Energy

\text{P$_1$}
\text{P$_2$}

When a mass m is displaced between locations P1 to P2

\text{($m$ @ $P_1$)$\rightarrow$ ($m$ @ $P_2$)}
= m\ (gy{_2}-gy{_1})

The mass of the object being displaced

The difference between the gravitational potential at the two points due to Earth

 Gravity analogy

\Delta U_g

The change in the Gravitational Potential Energy is given by:

= mgy{_2}-mgy{_1}

 Electrostatics

      The Electric Potential

            relationship to the Electric Potential Energy

\Delta V
q_0\ (V_{@P_2}-V_{@P_1})
\Delta U_\text{($q_0$ @ $P_1$)$\rightarrow$ ($q_0$ @ $P_2$)}=

The change in the Electric Potential Energy as some charge q0 is transferred from point P1 to point P2

The amount of net charge being transferred

The Electric Potential Difference between points P1 and P2

SI units: Substituting for

the charge in Coulombs, and

the Electric Potential in Volts,

results in the Energy in Joules

 Electrostatics

      The Electric Potential

            relationship to the Electric Potential Energy

\Delta V
\Delta U_\text{($q_0$ @ $P_1$)$\rightarrow$ ($q_0$ @ $P_2$)}= q_0\ (V_{@P_2}-V_{@P_1})

Electrostatics

The Electric Potential

and The Electric Field

 Electrostatics

Video walkthrough this stack

      The Electric Potential

           Relationship to the Electric Field

 Electrostatics

\vec{E}
V

The influence

of Electric Charges

      The Electric Potential

           Relationship to the Electric Field

\ \Delta V = \int \vec{E}\cdot d\vec{s}\
\ \vec{E}=-\vec{\nabla} V\

 Electrostatics

      The Electric Potential

           Relationship to the Electric Field

The Electric Field ~ the slope of the Electric Potential

\Delta V
\Delta s
\Delta V
\Delta s

 Electrostatics

      The Electric Potential

           Relationship to the Electric Field

\vec{E}
V
\ \vec{E}=-\vec{\nabla} V\
\Delta s
\Delta V
V_1
V_2
s_1
s_2

The average Electric Field

\vec{E}_\text{avg}=-\frac{~~~~~~~~}{~~~~~~~}\ \hat{s}
\Delta V
\Delta s

magnitude = Electric Potential Difference per unit length.

direction = from High potential to Low potential

V
s

 Electrostatics

      The Electric Potential

           Relationship to the Electric Field

V
s
s_1
s_2
V_1
V_2
\Delta s
\Delta V
\vec{E}
V
\ \vec{E}=-\vec{\nabla} V\
s_3
\vec{E}=-\ \frac{~~~~~~}{~~~~~}\ \hat{s}
d V
d s

The local Electric Field

\ \vec{E}=-\vec{\nabla} V\

In higher dimensions

Math Interlude

      Differential Calculus

           The Gradient (aka Del) Operator

\vec{\nabla} f{\small (r,\theta,\phi)}= \tfrac{\partial f}{\partial r}\ \hat{r} + \tfrac{1}{r}\tfrac{\partial f}{\partial \theta}\ \hat{\theta} + \tfrac{1}{r \sin\theta}\tfrac{\partial f}{\partial \phi}\ \hat{\phi}

Spherical Coordinates

\vec{\nabla} f{\small (x,y,z)}= \tfrac{\partial f}{\partial x}\ \hat{i} + \tfrac{\partial f}{\partial y}\ \hat{j} + \tfrac{\partial f}{\partial z}\ \hat{k}

Cartesian Coordinates

\vec{\nabla} f{\small (x,y,z)}= \tfrac{\partial f}{\partial x}\ \hat{i} + \tfrac{\partial f}{\partial y}\ \hat{j} + \tfrac{\partial f}{\partial z}\ \hat{k}

Cartesian Coordinates

h{\small (x,y,z)}= ay+b
\vec{\nabla} h{\small (x,y,z)}= \tfrac{\partial h}{\partial x}\ \hat{i} + \tfrac{\partial h}{\partial y}\ \hat{j} + \tfrac{\partial h}{\partial z}\ \hat{k}
= 0\ \hat{i} ~~+~ a\ \hat{j} ~~+~ 0\ \hat{k}
f{\small (x,y,z)}= axy^2+x^2 z
\vec{\nabla} f{\small (x,y,z)}=
+ x^2\ \hat{k}
+2axy\ \hat{j}
(ay^2+2xz) \hat{i}
\tfrac{\partial f}{\partial x}\ \hat{i}
+ \tfrac{\partial f}{\partial y}\ \hat{j}
+ \tfrac{\partial f}{\partial z}\ \hat{k}
=

Math Interlude

      Differential Calculus

           The Gradient (aka Del) Operator

\vec{\nabla} f{\small (r,\theta,\phi)}= \tfrac{\partial f}{\partial r}\ \hat{r} + \tfrac{1}{r}\tfrac{\partial f}{\partial \theta}\ \hat{\theta} + \tfrac{1}{r \sin\theta}\tfrac{\partial f}{\partial \phi}\ \hat{\phi}

Spherical Coordinates

Math Interlude

      Differential Calculus

           The Gradient (aka Del) Operator

\vec{\nabla} f{\small (r,\theta,\phi)}=
\tfrac{\partial f}{\partial r}\ \hat{r}
+ \tfrac{1}{r}\tfrac{\partial f}{\partial \theta}\ \hat{\theta}
+ \tfrac{1}{r \sin\theta}\tfrac{\partial f}{\partial \phi}\ \hat{\phi}
{\small \sin\phi}\ \hat{r}
\small +0\ \hat{\theta}
=
- \tfrac{r\cos\phi}{r \sin\theta}\ \hat{\phi}
\vec{\nabla} V{\small (r,\theta,\phi)}=
\tfrac{\partial V}{\partial r}\ \hat{r}
+ \tfrac{1}{r}\tfrac{\partial V}{\partial \theta}\ \hat{\theta}
+ \tfrac{1}{r \sin\theta}\tfrac{\partial V}{\partial \phi}\ \hat{\phi}
=
-\tfrac{kq}{r^2}\ \hat{r}
\small +0\ \hat{\theta}
\small +0\ \hat{\phi}
\vec{E}=\tfrac{kq}{r^2}\ \hat{r}
V=\tfrac{kq}{r}
\ \vec{E}=-\vec{\nabla} V\

For a point charge

f{\small (r,\theta,\phi)}= r \sin\phi
V{\small (r,\theta,\phi)}= \tfrac{kq}{r} + V_0