Electromagnetic Waves

Traveling disturbances in the Electric and Magnetic Fields

Maxwell's Equations

Electromagnetic Waves

Oscillations in the Electric & Magnetic Fields

 Electromagnetic Waves

      Maxwell's Equations

           Introduction

James Clerk Maxwell, a 19th-century physicist, developed a theory that explained the relationship between electricity and magnetism

 Electromagnetic Waves

      Maxwell's Equations

           Gauss' Law

\oint\vec{E}\cdot d\vec{A}=\frac{q_\text{enc}}{\epsilon}
+

Positive charges are "sources" of Electric Fields

-

Negative Charges are "sinks" of Electric Fields

Electric flux through a closed surface is proportional to the enclosed charge

\vec{\nabla}\cdot\vec{E}=\frac{\rho}{\epsilon}

The divergence of the field around any point is related to the charge density at that point.

Electric Charges create Electric Fields.

 Electromagnetic Waves

      Maxwell's Equations

           No Magnetic Monopoles

There exists no magnetic monopoles in nature

\oint\vec{B}\cdot d\vec{A}=0

Magnetic flux through a closed surface is zero

\vec{\nabla}\cdot\vec{B}=0

The divergence of the magnetic field around any point is zero.

 Electromagnetic Waves

      Maxwell's Equations

           Faraday's Law

Faraday's Law

but

\mathcal E=-\frac{d\Phi_m}{dt}
\oint\vec{E}\cdot d\vec{s}=\frac{d\Phi_m}{dt}

Varying magnetic fields generate electric fields

\vec{E}
V
\ \Delta V = -\int \vec{E}\cdot d\vec{s}\
\vec{\nabla}\times\vec{E}=-\frac{\partial B}{\partial t}

The rate of change of the magnetic field is equivalent to the curl of the electric field.

A changing magnetic flux induces electric fields

 Electromagnetic Waves

      Maxwell's Equations

           Ampere's Law

Ampere's Law

\oint\vec{B}\cdot d\vec{s}=\mu I_\text{enc}
\oint\vec{B}\cdot d\vec{s}=\mu I_\text{enc}+\mu\epsilon\frac{d\Phi_E}{dt}
\oint\vec{B}\cdot d\vec{s}=\mu (I_\text{enc}+I_d)

Ampere's Law - modified

Magnetic Fields are generated by moving Charges or varying Electric Fields

 Electromagnetic Waves

      Maxwell's Equations

           Putting it together

\oint\vec{B}\cdot d\vec{s}=\mu I_\text{enc}+\mu\epsilon\frac{d\Phi_E}{dt}

Moving Charges and/or varying Electric Fields generate Magnetic Fields.

\oint\vec{E}\cdot d\vec{s}=\frac{d\Phi_m}{dt}

Varying Magnetic Fields generate Electric Fields.

Magnetic monopoles do not exist.

\oint\vec{B}\cdot d\vec{A}=0
\oint\vec{E}\cdot d\vec{A}=\frac{q_\text{enc}}{\epsilon}

Electric Charges create Electric Fields.

 Electromagnetic Waves

      Maxwell's Equations

           Putting it together

Watch this video if you're interested in learning more about divergence and curl.

 Electromagnetic Waves

      Maxwell's Equations

           The Lorentz force

\vec{F}=q\vec{E}+q\vec{v}\times\vec{B}

Once the fields are found, we can calculate the force on a charged particles using the Lorentz force expression:

Speed of electromagnetic waves

Electromagnetic Waves

Traveling disturbance in the Electric and Magnetic Fields

 Electromagnetic Waves

      Maxwell's Equations

           Putting it together

Two straight conductors connected to the terminals of an AC generator

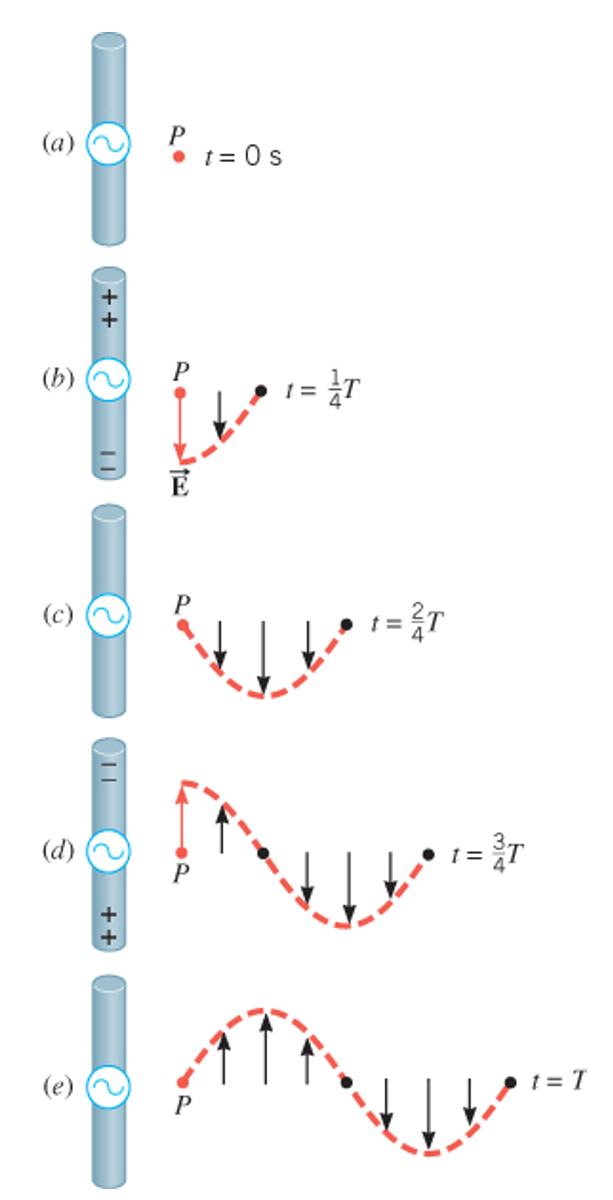
generate electric fields that vary harmonically

 Electromagnetic Waves

      Maxwell's Equations

           Putting it together

A current flowing through a conductor

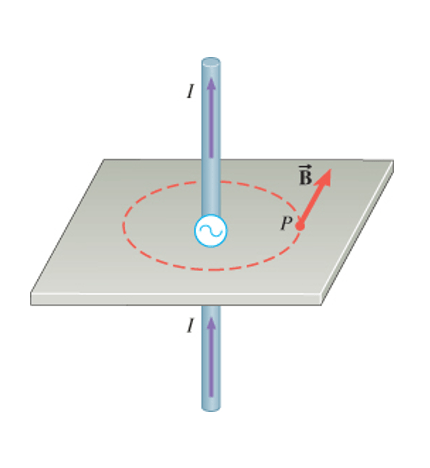
generates a magnetic field that is proportional to the current.

 Electromagnetic Waves

      Maxwell's Equations

           Putting it together

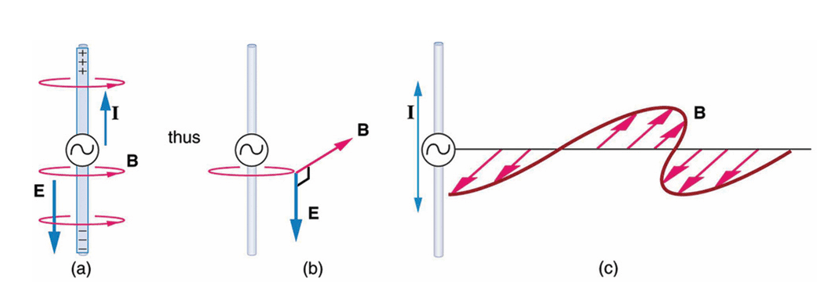
A current flowing through a conductor

creates simultaneous electric and magnetic fields that are perpendicular to each other.

 Electromagnetic Waves

      Maxwell's Equations

           Putting it together

A time-varying magnetic field induces an electric field

A time-varying electric    field induces a magnetic field

 Electromagnetic Waves

      Maxwell's Equations

           Putting it together

A disturbance in the electromagnetic fields propagates away from the location it is created: Electromagnetic Wave 

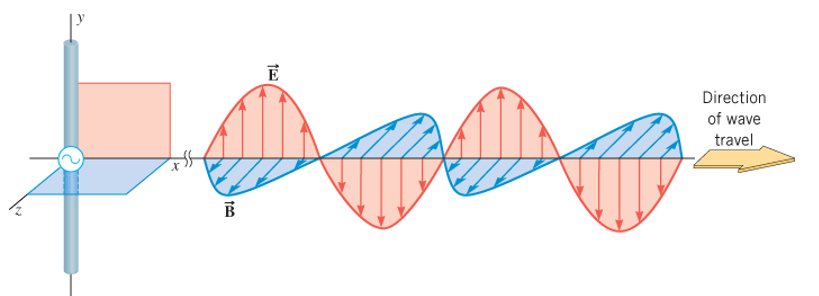
 Electromagnetic Waves

      Maxwell's Equations

           Putting it together

In general, the speed of any wave depends on the properties of the medium.

c=\tfrac{1}{\sqrt{\epsilon_0 \mu_0}}

From Maxwell's equations, a disturbance in the electromagnetic fields travels at a speed given by:

v=\tfrac{1}{\sqrt{\epsilon \mu}}
=\frac{1}{\sqrt{(8.8542\times10^{-12})(4\pi\times10^{-7})}}
=299\ 792\ 250\ \text{m/s}

In vacuum:

\approx 3\times10^8\ \text{m/s}

 Electromagnetic Waves

      Maxwell's Equations

           Putting it together

"This velocity is so nearly that of light, that it seems we have strong reasons to conclude that light itself (including radiant heat, and other radiations if any) is an electromagnetic disturbance in the form of waves propagated through the electromagnetic field according to electromagnetic laws."

James Clerk Maxwell, 1865

Wave properties

Electromagnetic Waves

Traveling disturbance in the Electric and Magnetic Fields

          What is a wave?

Classically, a wave is defined as a traveling disturbance that carries energy.

E.g. a wave on a string is a disturbance in the vertical position of the beads travelling along the string (via tension) carrying mechanical energy.

For a traveling harmonic wave

At a specific instant in time, describe the disturbance as a function of position:

y(x,t_0)=Y \sin(\frac{2\pi}{\lambda}x+\phi_t)

where      is the wavelength (distance from peak to peak in a snapshot)

\lambda

At a specific location, describe the disturbance as a function of time:

y(x_0,t)=Y \sin(\frac{2\pi}{T}t+\phi_x)

where      is the period (time of one cycle, at a specific location.)

T

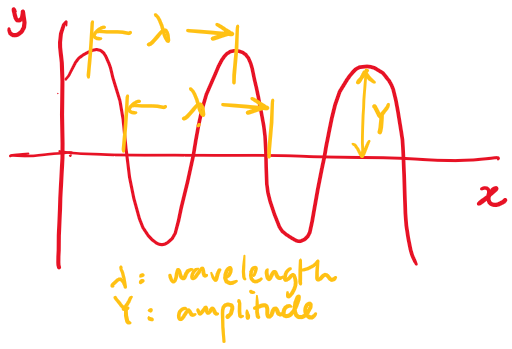
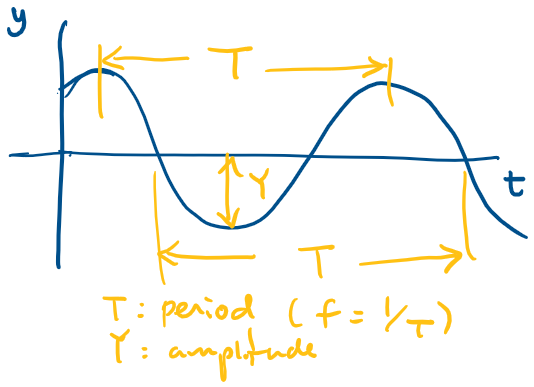
Electromagnetic waves

    Wave motion

          What is a wave?

Electromagnetic waves

    Wave motion

          The wave equation

For a traveling harmonic wave

The Classical Wave Equation!

y(x,t)=Y \sin(\frac{2\pi x}{\lambda}- \frac{2\pi t}{T}+\phi)
= Y \sin(kx- \omega t+\phi)

where:

: wave number

: angular frequency

: amplitude

: phase constant

k
\omega
Y
\phi

Q: find the relationship between

\frac{\partial^2 y}{\partial x^2}
\frac{\partial^2 y}{\partial t^2}

and

\frac{\partial^2 y}{\partial x^2} = -k^2 y
\frac{\partial^2 y}{\partial t^2} = -w^2 y
\frac{\partial^2 y}{\partial x^2} = \frac{k^2}{\omega^2} \frac{\partial^2 y}{\partial t^2}
\frac{\partial^2 y}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 y}{\partial t^2}

Electromagnetic waves

    Wave motion

          Wave properties

For a traveling harmonic wave

The speed of the wave:

v=f\lambda

The speed of the wave:

c=f\lambda

For an electromagnetic wave in vacuum

The amplitudes of the wave:

c=E_0/B_0

Electromagnetic waves

    Wave motion

Electromagnetic waves

    Wave motion

          The electromagnetic spectrum

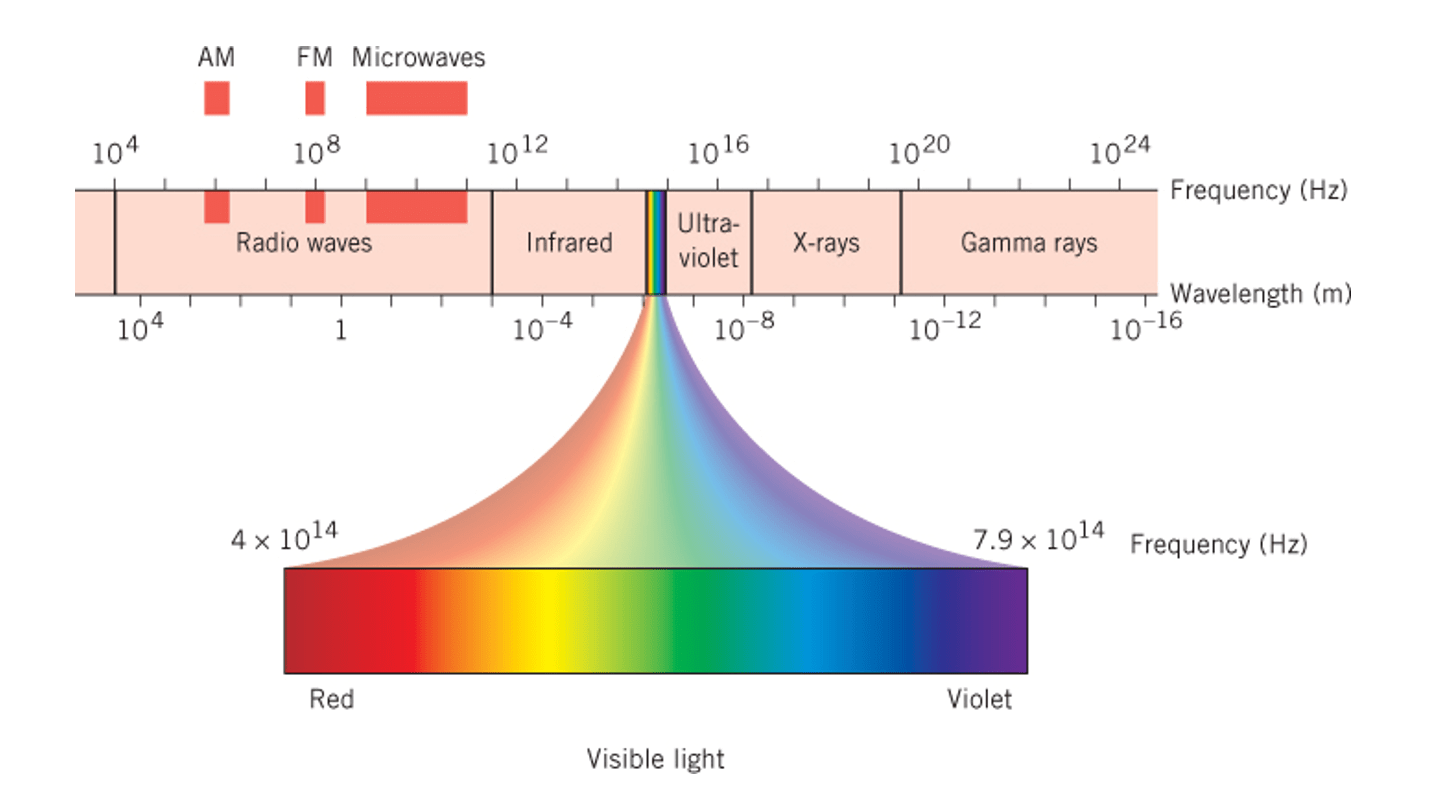
Energy in EM waves

Electromagnetic Waves

Traveling disturbance in the Electric and Magnetic Fields

The energy stored in the electric field in the volume between the plates of a parallel plate capacitor is given by

 EM-waves

      Energy & Intensity

           How much energy does an EM wave carry?

U=\tfrac{1}{2}CV^2
=\tfrac{1}{2}\frac{\epsilon_0 A}{d}E^2d^2
V=\int E\ ds=E\ d
C=\frac{\epsilon_0 A}{d}
=\tfrac{1}{2}\epsilon_0E^2Ad

The energy density stored in the electric field:

 EM-waves

      Energy & Intensity

           How much energy does an EM wave carry?

u=U/\text{volume}
u=\frac{1}{2}\epsilon_0E^2

The energy density stored in the magnetic field:

 EM-waves

      Energy & Intensity

           How much energy does an EM wave carry?

u=\frac{1}{2\mu_0}B^2

 EM-waves

      Energy & Intensity

           How much energy does an EM wave carry?

For an electromagnetic wave, for a sample volume, which field carries more share of the energy (E or B) ?

 EM-waves

      Energy & Intensity

           How much energy does an EM wave carry?

u=\frac{1}{2\mu_0}B^2
u=\frac{1}{2}\epsilon_0E^2

The energy carried by the wave per unit area per unit time is called the energy flux S:

 EM-waves

      Energy & Intensity

           How much energy does an EM wave carry?

S=\frac{1}{\mu_0}EB

Taking the direction of propagation into account, we get the Poynting vector:

\vec{S}=\frac{1}{\mu_0}\vec{E}\times\vec{B}

For an electromagnetic wave given by:

 EM-waves

      Energy & Intensity

           How much energy does an EM wave carry?

E(t)=E_0 \sin(\omega t)

We define the intensity as the average flux density over one cycle

I=S_\text{avg}=\frac{c}{2}\epsilon_0E_0^2 =\frac{c}{2 \mu_0}B_0^2
B(t)=B_0 \sin(\omega t)

 EM-waves

      Energy & Intensity

           How much energy does an EM wave carry?

A plane electromagnetic wave travels northward. At one instant, its electric field has a magnitude of 6.0 V/m and points eastward. What are the magnitude and direction of the magnetic field at this instant?

 EM-waves

      Energy & Intensity

           How much energy does an EM wave carry?

The beam from a small laboratory laser has a radius of 2.0mm and a power of 15.0 mW. Assuming that the beam is composed of plane waves, calculate the amplitudes of the electric and magnetic fields in the beam.

 EM-waves

      Energy & Intensity

           How much energy does an EM wave carry?

A light bulb emits 5.00 W of power as visible light. What are the electric and magnetic fields from the light at a distance of 3.0 m?



 EM-waves

      Energy & Intensity

           How much energy does an EM wave carry?

A 150-W lightbulb emits 5% of its energy as electromagnetic radiation. What is the magnitude of the average Poynting vector 10 m from the bulb?

 

 

Electromagnetic waves

    Energy in EM waves

          The energy density