Magnetism
The interaction of moving charges

Charged Particles
- influence is described in terms of
The influence
and interactions
of
Story so far was about
Electric
Fields

3-D Electric Field Caused by two identical Point Charges
- interaction is described in terms of
Electric
Forces
Magnetism
Charged Particles
The influence
and interactions
of
Today's story...
moving

3-D Electric Field Caused by two identical Point Charges
Magnetism
- influence is described in terms of
Magnetic
Fields
- interaction is described in terms of
Magnetic
Forces
Magnetism
Introduction
Intrinsic Magnetism
Magnetism
I. Sources of Magnetic Fields
Magnetism
Sources of Magnetic Fields
Intrinsic Magnetism

Electric charges in motion
Magnetism
I. Sources of Magnetic Fields
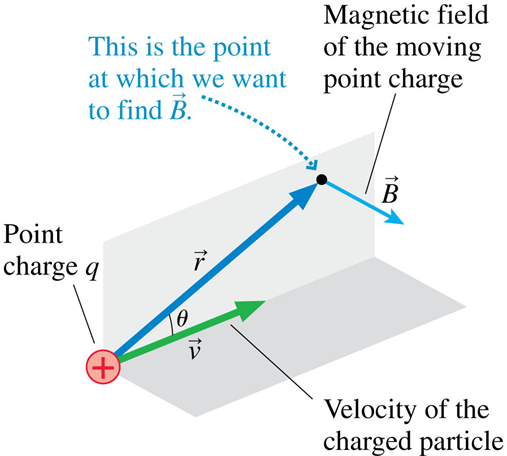

Direction is given by
Magnitude is given by
Magnetism
Sources of Magnetic Fields
Biot-Savart Law
Right-Hand-Rule

Direction is given by
Magnitude is given by
Magnetism
Sources of Magnetic Fields
Biot-Savart Law
Right-Hand-Rule


Direction is given by
Magnitude is given by
Magnetism
Sources of Magnetic Fields
Biot-Savart Law
Right-Hand-Rule
Sources are moving charges–if the velocity is zero, the magnetic field is zero!
–
Superposition principle applies–just like electric fields, magnetic field vectors add linearly!
–
Magnetic field strength has inverse square dependence on the distance from the moving charge
Magnetism
Sources of Magnetic Fields
Biot-Savart Law -- example


Magnitude is given by
Magnetism
Sources of Magnetic Fields
Biot-Savart Law -- example


Magnitude is given by
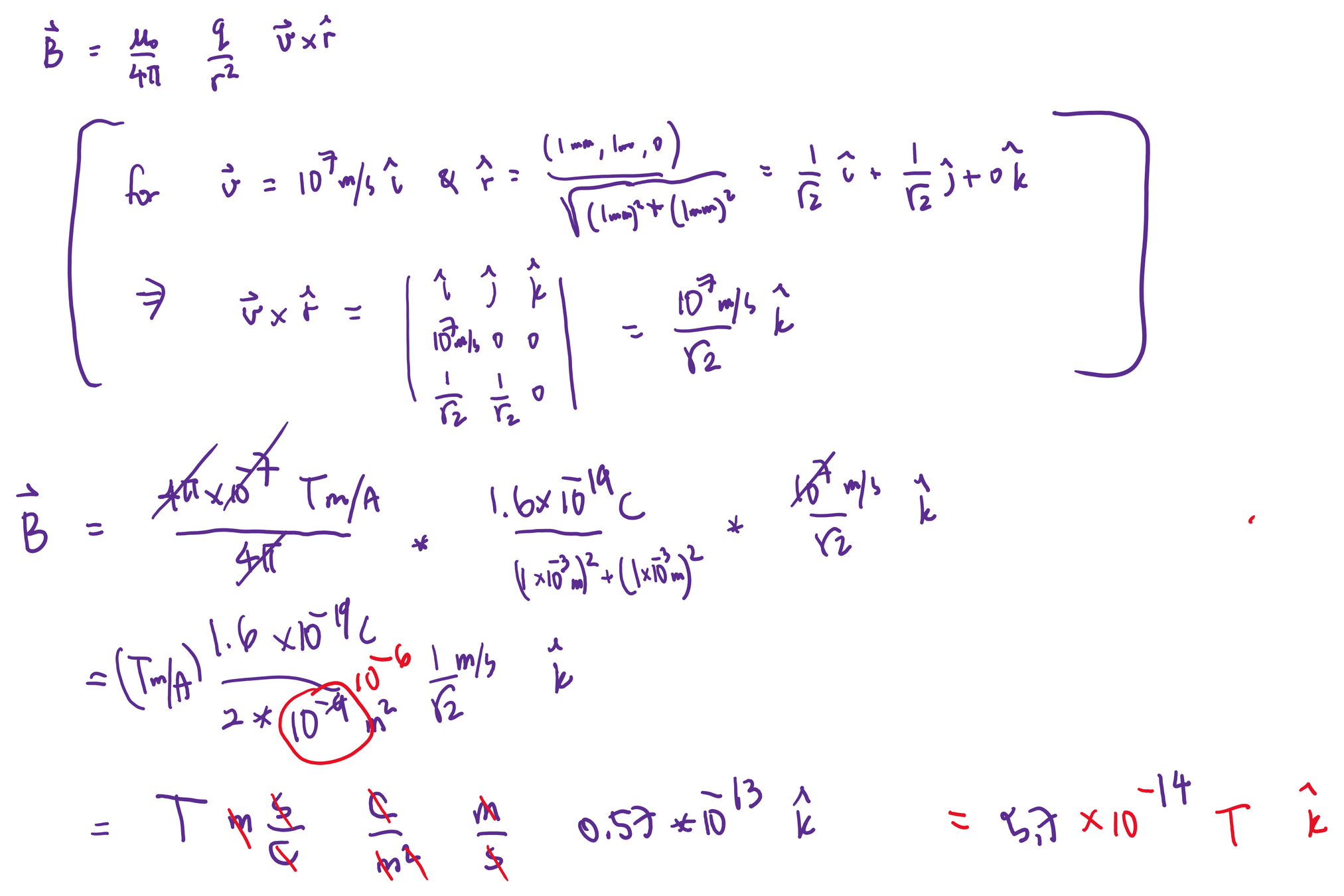
Magnetic Field Lines
Magnetism
I. Sources of Magnetic Fields
Magnetism
Sources of Magnetic Fields
Magnetic Field Lines
Magnetism
Sources of Magnetic Fields
Magnetic Field Lines
animation from National MagLab
Electric Currents
Magnetism
I. Sources of Magnetic Fields
Magnetism
Sources of Magnetic Fields
Biot-Savart Law
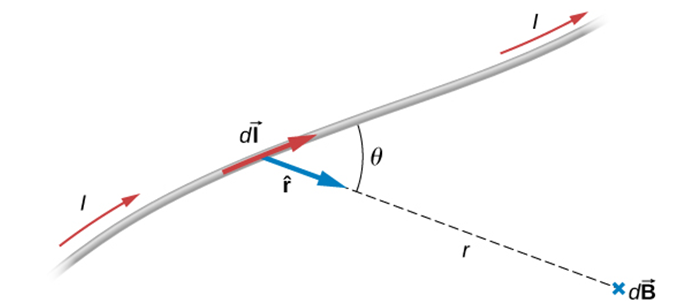
Biot-Savart Law
Magnetic Field due to a Current Segment
Magnetism
Sources of Magnetic Fields
Biot-Savart Law

Magnetism
Sources of Magnetic Fields
Biot-Savart Law
Magnetic Field due to a thin straight wire
Magnetism
Sources of Magnetic Fields
Biot-Savart Law
Magnetic Field on the axis of a circular loop
Magnetism
Sources of Magnetic Fields
Biot-Savart Law
Magnetic Field on the axis of a solenoid
Biot-Savart Law
Magnetism
Sources of Magnetic Fields
Biot-Savart Law -- TL;DR
a distance d away from a Long straight segment
@ center of Circular Loop
On the axis of a circular Loop
On the axis of a solenoid
Magnetic Force on a moving charge -- The Rules
Magnetism
II. Magnetic Forces
Magnetism
Magnetic Forces
Magnetic Force on a moving charge

Magnetism
Magnetic Forces
Magnetic Force on a moving charge

Magnetism
Magnetic Forces
Magnetic Force on a moving charge

Magnetism
Magnetic Forces
Magnetic Force on a moving charge

Magnetism
Magnetic Forces
Magnetic Force on a moving charge

on (+) charges
on (-) charges
Magnetism
Magnetic Forces
Magnetic Force on a moving charge

An electron travelling at 20% the speed of light in a direction 30 degrees North of East, passes through a region where Earth’s magnetic field is uniform, pointing North, with a magnitude of 50µT. What is (the magnitude and direction of) the magnetic force experienced by the electron?
The trajectory of charged particles in uniform magnetic fields
Magnetism
II. Magnetic Forces
Magnetism
Magnetic Forces
Particle trajectory

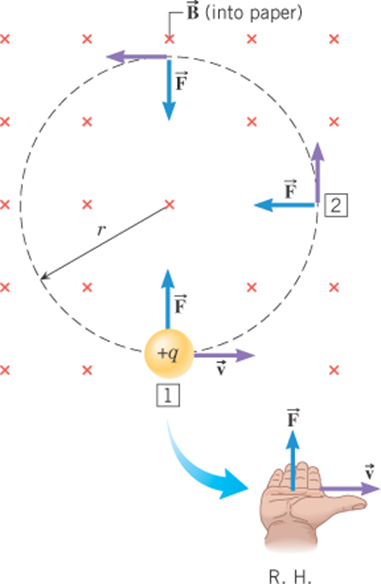
Consider a charged particle traveling perpendicular to a uniform magnetic field.
The particle experiences a magnetic force in a direction given by the right-hand-rule.
The trajectory of the particle follows a circular arc at a constant speed.
+
+
+
An acceleration perpendicular to the direction of motion will only change the direction of motion.
The change in the direction of motion induces a change in the direction of the force (& acceleration)
Magnetism
Magnetic Forces
Particle trajectory


+
+
+
The magnetic force acts as a centripetal force, keeping the charge in a circular arc of radius R
The radius, R, depends on:
m and q (mass and net charge) are intrinsic quantities related to the particle itself,
v is the speed of the particle (which is related to its kinetic energy)
B is the strength of the magnetic field (aka magnetic flux density)
Magnetism
Magnetic Forces
Particle trajectory


+
+
+
The magnetic force acts as a centripetal force, keeping the charge in a circular arc of radius R
The radius of the circular trajectory
net electric charge
magnetic field strength
component of velocity
mass
Magnetism
Magnetic Forces
Particle trajectory
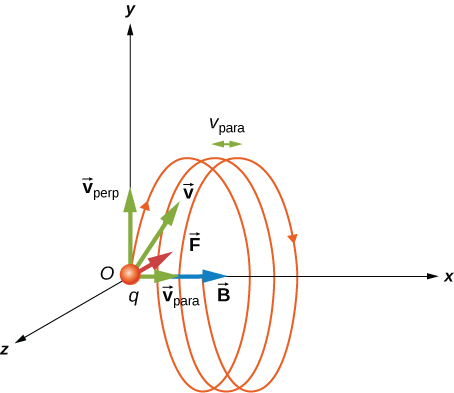
In general, the particle's motion can be decomposed into components:
The component parallel to the magnetic field is unchanged by its interaction with the field
The resulting motion is helical about the direction of the magnetic field
The component perpendicular to the magnetic field undergoes uniform circular motion.
Magnetism
Magnetic Forces
Particle trajectory
The basic cause of Aurora involves the interaction of the solar wind with Earth's magnetosphere
Magnetism
Magnetic Forces
Magnetic Force on a moving charge
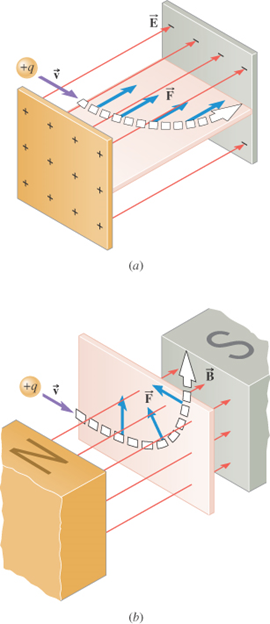
The electric force
is parallel to
the electric field
The magnetic force
is perpendicular to
the magnetic field
Magnetism
Magnetic Forces
Magnetic Force on a moving charge

The electric force
is not perpendicular to
the motion
The magnetic force
is perpendicular to
the motion
particle speeds up or slows down
particle changes direction of motion
Magnetic Force on a moving charge -- Applications
Magnetism
II. Magnetic Forces
Magnetism
Magnetic Forces
Particle trajectory
Application: Velocity Selector
A velocity selector is a device that allows charged particles with a particular velocity to pass through, while deflecting all other charged particles.
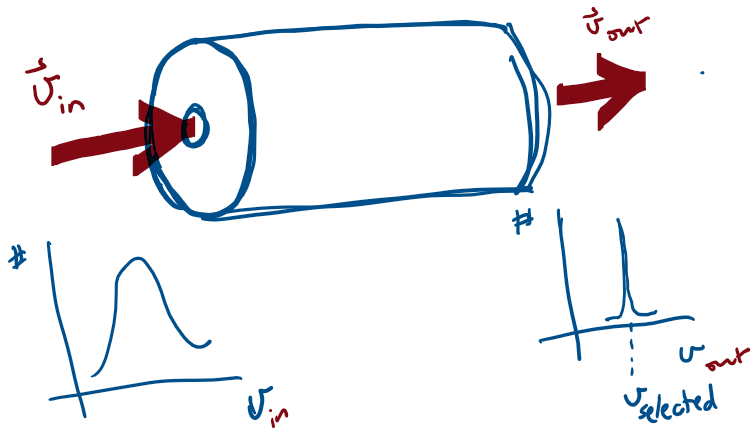
Magnetism
Magnetic Forces
Particle trajectory
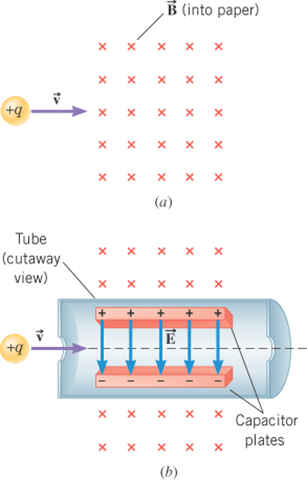

The device operates by applying electric and magnetic forces to the particle in such a way that these
forces balance.
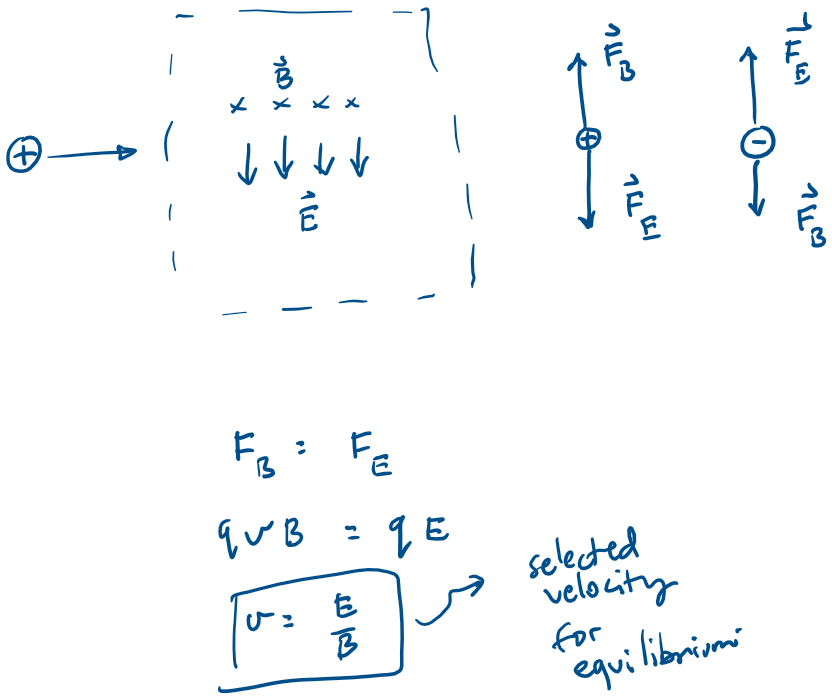
For the situation shown in the figure, how should an electric field be applied so that the force it applies to the particle can balance the magnetic force?
For the situation shown in the figure, what is the selected velocity?
Magnetism
Magnetic Forces
Particle trajectory - Hall Effect
Application: Hall Effect Sensors

Magnetism
Magnetic Forces
Particle trajectory - pair production

Charged
Particles
in
Cloud/Bubble
Chambers
Magnetism
Magnetic Forces
Particle trajectory - pair production

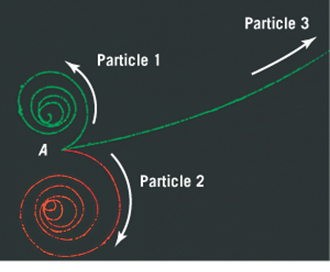
If the magnetic field is directed out of the "page"-- What are the signs of the charges of the three particles?
All 3 particles have the same mass and (magnitude of) charge-- which particle is initially moving most rapidly?
The particles follow a spiraling path -- Are we able to explain why?
The tracks going counter clockwise are left by negatively charged particles.
The bigger the speed, the bigger the radius (for same q, m and B)
Loss of energy (signified by loss of speed, leads to ever decreasing radius)
Magnetism
Magnetic Forces
Particle trajectory - the mass spectrometer
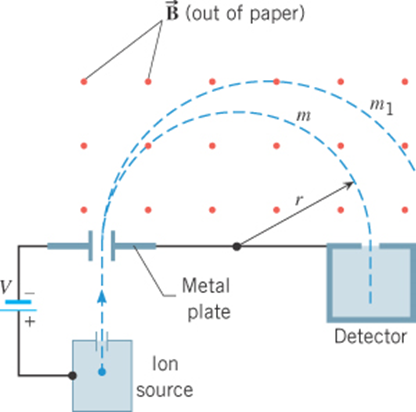
For fixed v, q, and B
Detector
particle injection
Magnetism
Magnetic Forces
Particle trajectory - the mass spectrometer

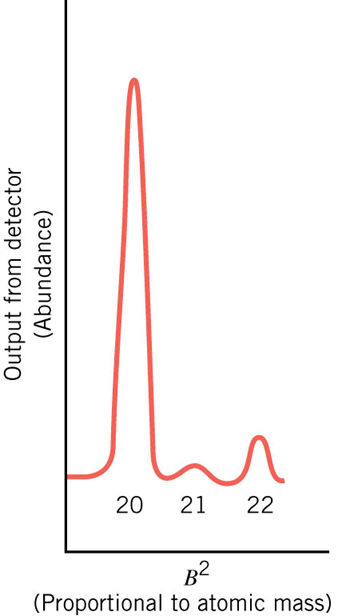

Magnetic Force on a current-carrying conductor
Magnetism
II. Magnetic Forces
Magnetism
Magnetic Forces
Magnetic Force on a current-carrying conductor
Consider a conductor carrying a an electric current in a region where there is a magnetic field
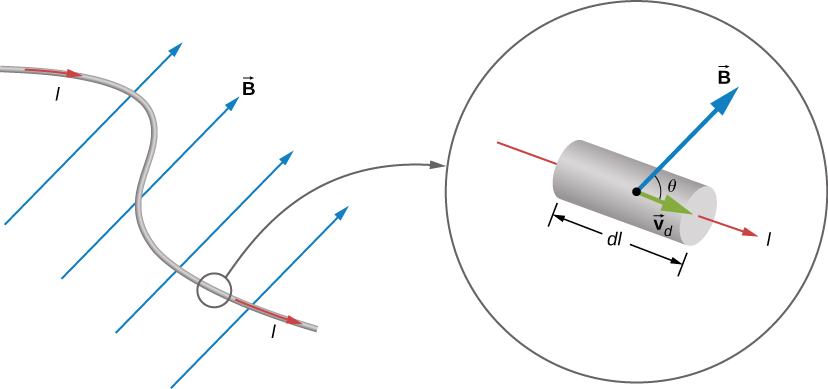

charges flowing inside the conductor will experience a magnetic force
Magnetism
Magnetic Forces
Magnetic Force on a current-carrying conductor
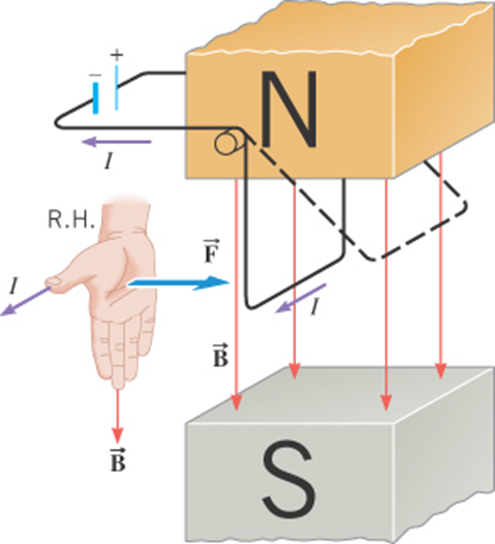
For a straight segment in a uniform magnetic field:
The Magnetic Force
electric current
magnetic field strength
angle between current & field
length of segment
Torque on a current-carrying loop
Magnetism
II. Magnetic Forces
Magnetism
Magnetic Forces
Torque on a current-carrying loop
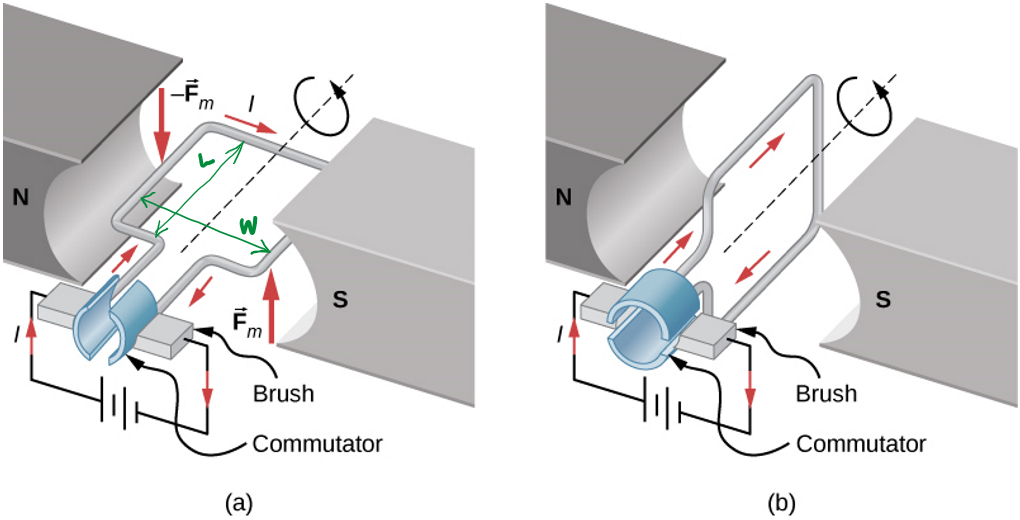
Consider a rectangular loop, L x W, carrying a current I, in a uniform magnetic field of strength B
The magnitude of the force on each arm of the loop is given by
These forces are in opposite directions, as given by the RHR
Magnetism
Magnetic Forces
Torque on a current-carrying loop
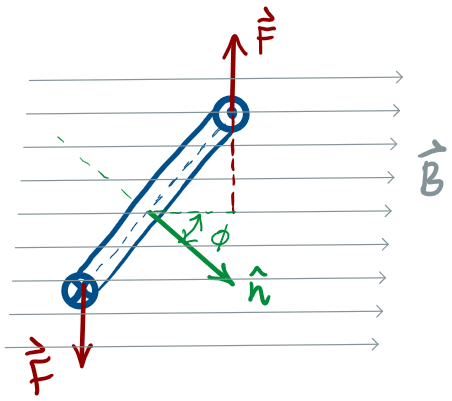
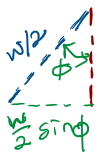
To calculate the net torque about the axis of rotation, consider the situation where the normal to the loop makes an angle with the magnetic field:
where

Magnetism
Magnetic Forces
Torque on a current-carrying loop
Notice that the torque follows the sin function
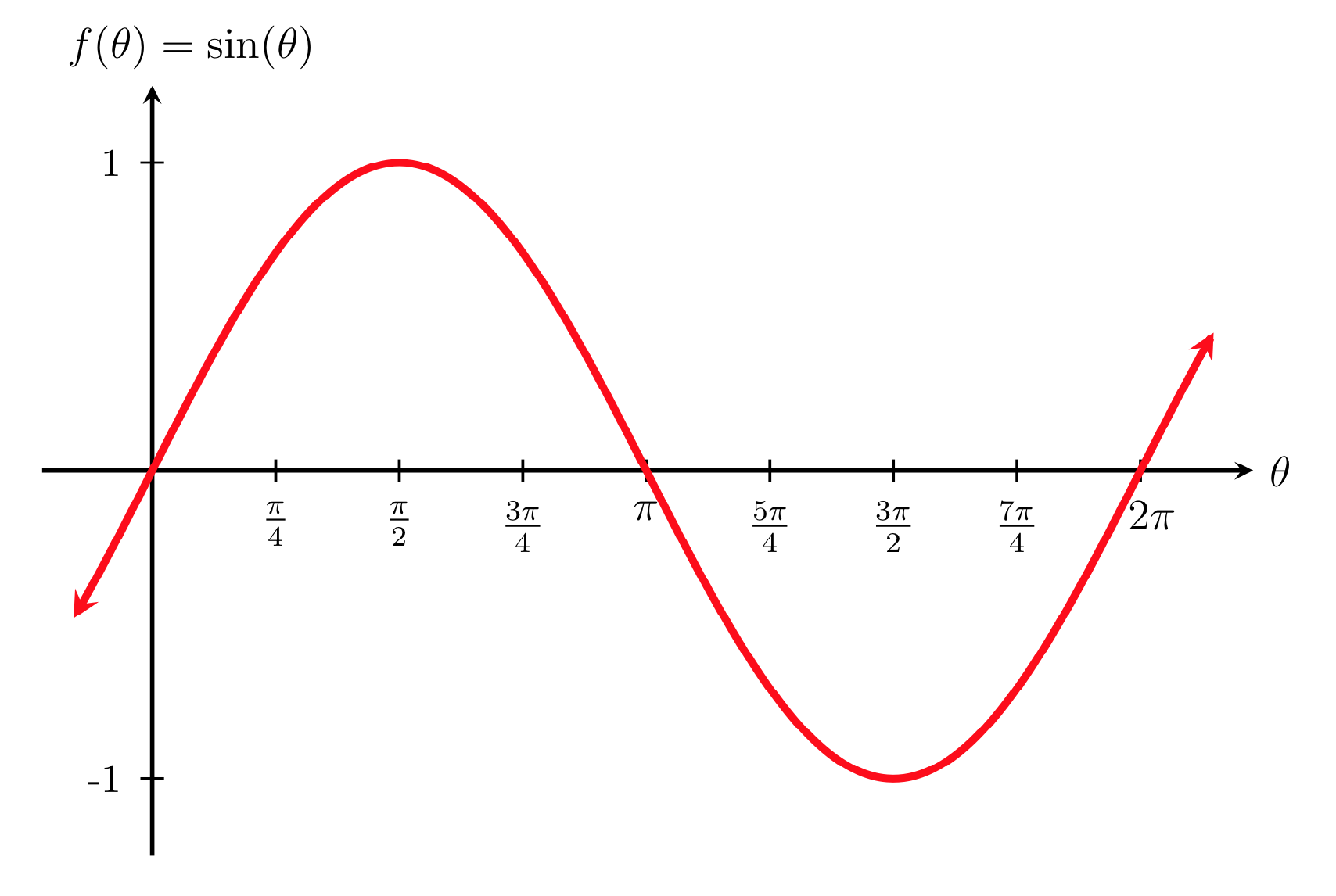
The torque on a current loop is a restoring torque!
(i.e. tends to align the normal to the loop with the field!)
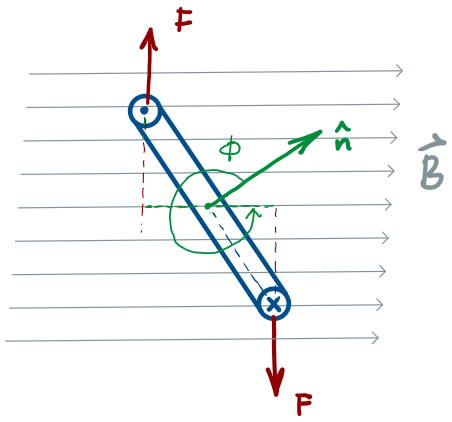
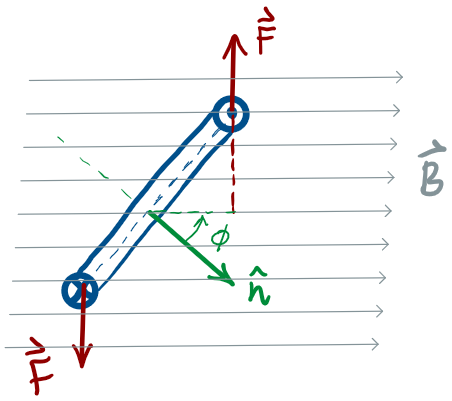
no torque when
Magnetism
Magnetic Forces
Torque on a current-carrying loop
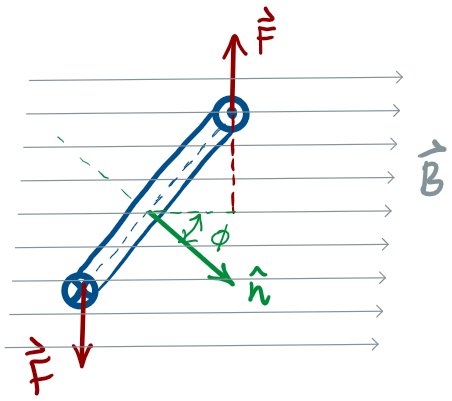
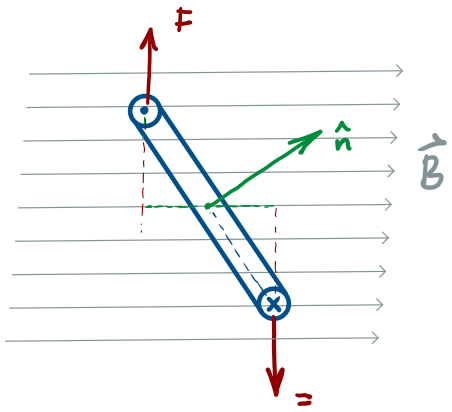

If you want to generate rotational motion, Opposite
Torques is a problem!
(Genius)
Solution:
Brush!
