Creative
Computation
for Visual
Communication
Design
WEEK 4 DAY 2
Coding Workshop
4.2
What did we learn?
- Arrays
- Declaring arrays
- Accessing elements in array
- Traversing arrays
- Loading text files
- Processing text
Custom shapes
-
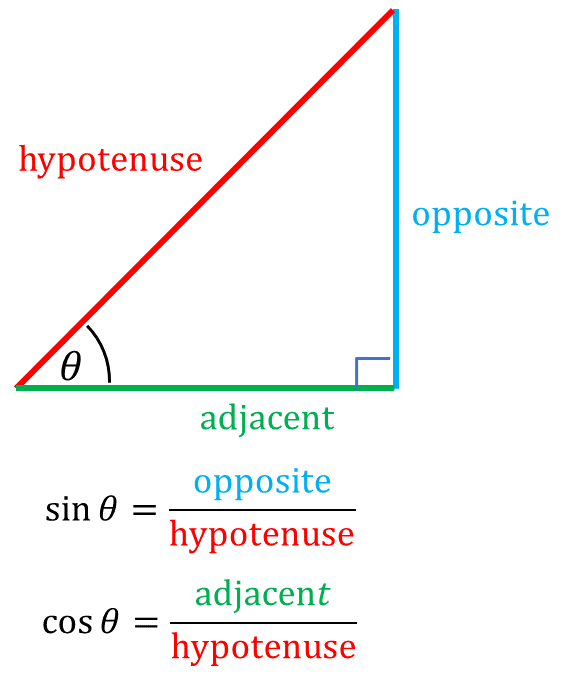
So far we have learned how to draw shapes with pre-existing functions (ellipse, rect, triangle)
-
You can also draw custom shapes with beginShape, endShape and vertex
- Draws angular shapes where every vertex point defines a corner
//add all vertex points between beginShape and endShape
beginShape();
vertex(x0, y0);
vertex(x1, y1);
vertex(x2, y2);
vertex(x3, y3);
endShape();
Custom shapes: Curves
-
You can draw continuous curves using curveVertex
-
This method draws so-called Catmull-Rom splines
-
At least four points are needed to draw one curve
-
The first and last point are used to control the curve
-
- Check the p5.js tutorial for Drawing curves
//add all vertex points between beginShape and endShape
beginShape();
curveVertex(x0, y0);
curveVertex(x1, y1);
curveVertex(x2, y2);
curveVertex(x3, y3);
endShape();
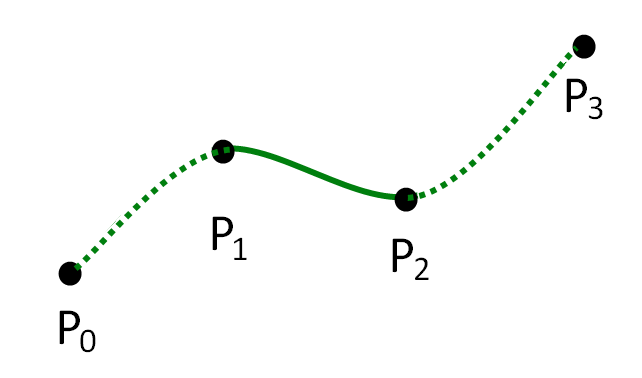
Custom shapes: Bezier curves
-
The first two parameters specify the first anchor point and the last two parameters specify the second anchor point
-
The middle parameters specify the two control points
-
Control points "pull" the curve towards them.
-
- Check the p5.js tutorial for Drawing curves
line(85, 20, 10, 10);
line(90, 90, 15, 80);
bezier(85, 20, 10, 10, 90, 90, 15, 80);bezier(x1, y1, x2, y2, x3, y3, x4, y4);
John Whitney: Experiments in Motion Graphics (1968)
John Whitney (1917–1995) was an American animator, composer and inventor, widely considered to be one of the fathers of computer animation.
Trigonometric functions
HOW TO CRERATE SMOOTHLY LOOPING ANIMATIONS?
HOW TO CALCULATE POINTS ON A CIRCLE?


HOW TO DRAW
WAVEFORMS?
Trigonometric functions
REMEMBER THESE?
DON'T WORRY!
WE ARE DOING SOMETHING DIFFERENT!
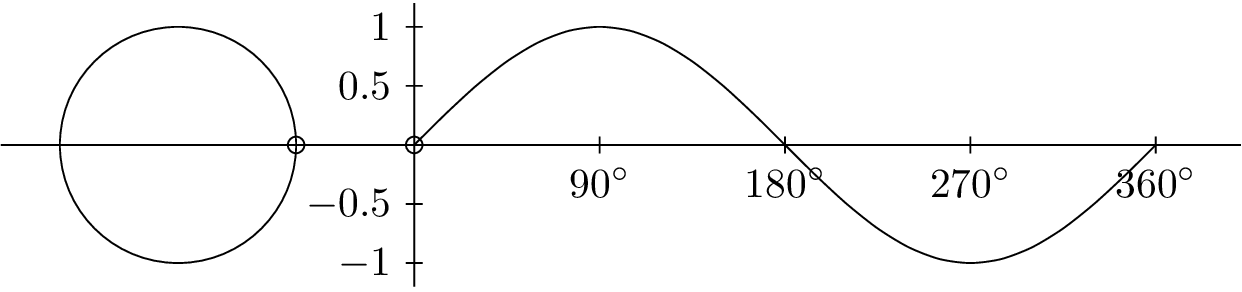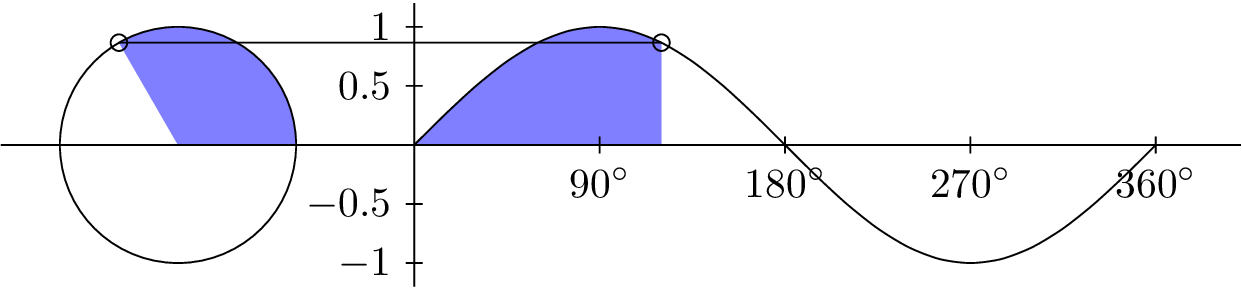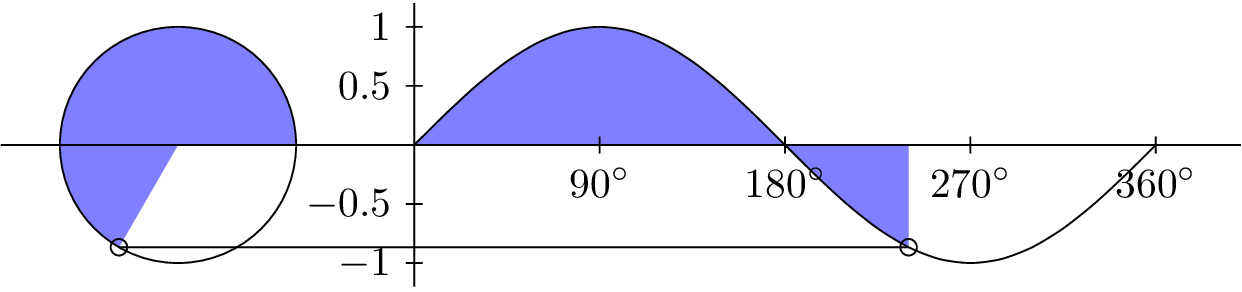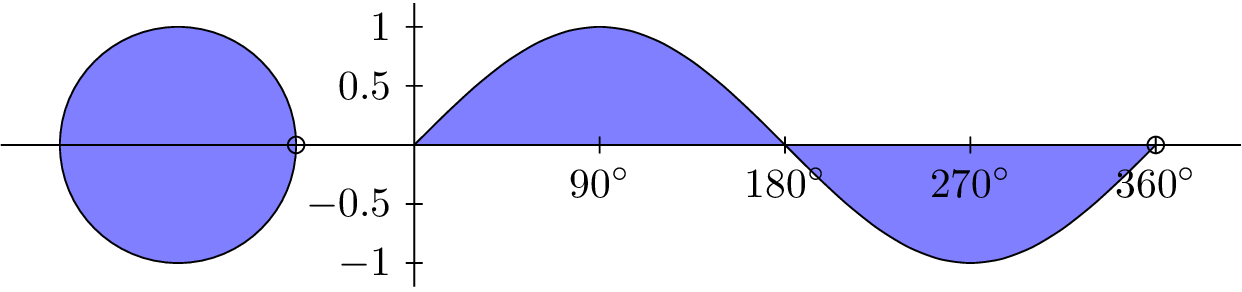
Sine function:
A NUMBER GRINDER
WHATEVER YOU PUT IN,
YOU ALWAYS GET OUT VALUES BETWEEN -1 AND 1!

INPUT:
LINEAR SEQUENCE
(1,2,3…)
OUTPUT:
OSCILLATING
SEQUENCE
(-1 TO 1)
sin()
INPUT:
ANGLE θ
from 0° to 360
OUTPUT:
SINE CURVE
sin(θ)
from -1 to 1
Sine function:
A NUMBER GRINDER
FULL CIRCLE = 360° = 2π rad
HALF CIRCLE = 180° = π rad
90° = π/2 rad
Radians
angleMode(RADIANS); //default
angleMode(DEGREES);
degrees(PI); //returns 180
radians(180); //returns 3.14159...
INPUT:
ANGLE θ
from 0 to 2π rad
OUTPUT:
SINE CURVE
sin(θ)
from -1 to 1
Radians
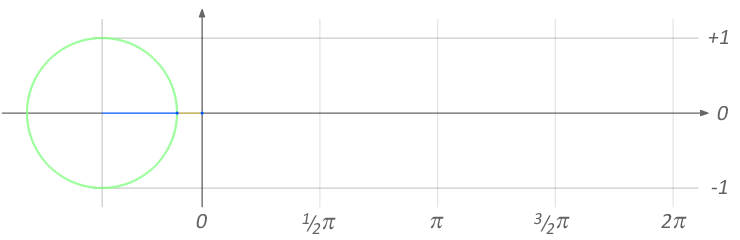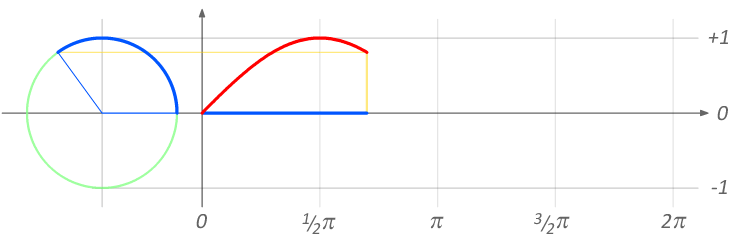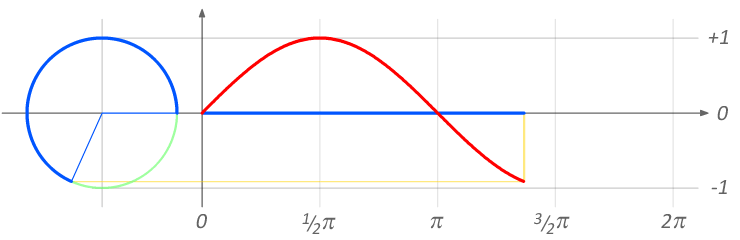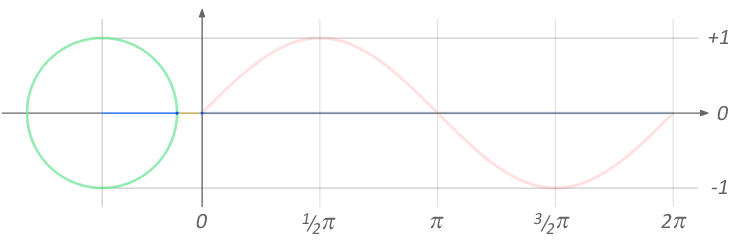
Exercise 1a: Simple sine animations
VARIATION: Exercise 1B:
Multiple sine animations
- Animate multiple different effects with sine!
- Position, size, colour, you name it!
Waveform
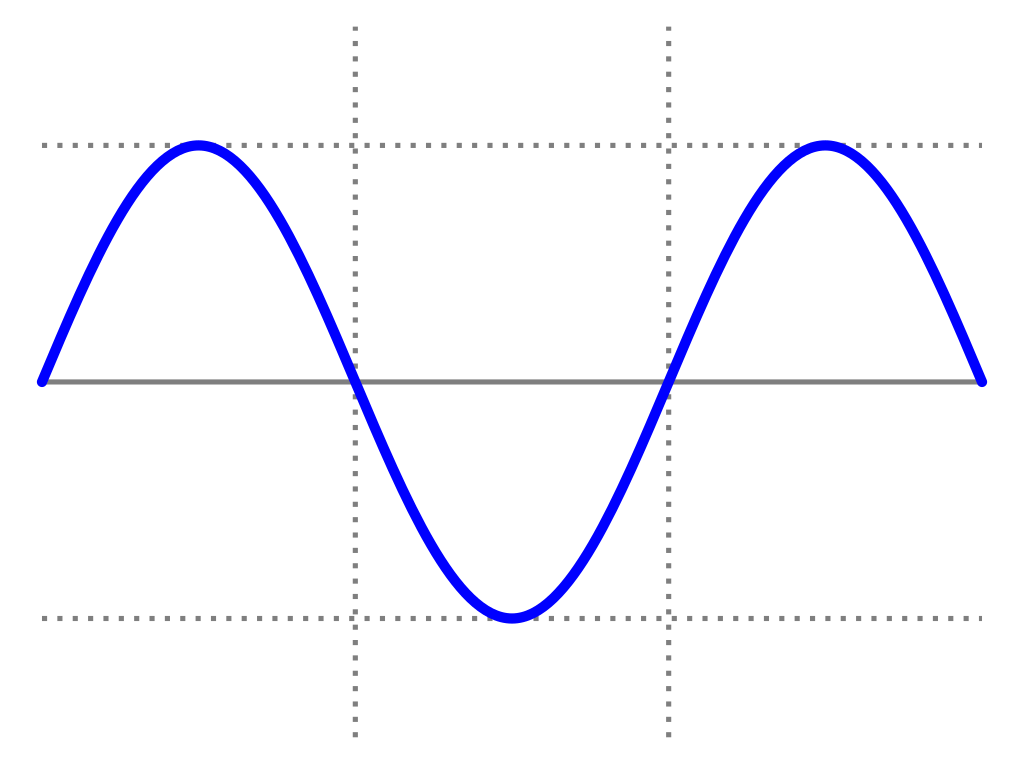
-
PHASE describes the starting position of the wave
-
AMPLITUDE describes the wave range
-
PERIOD describes the length of one cycle
-
FREQUENCY describes how often wave repeats (= 1/PERIOD)
PHASE
PERIOD
AMPLITUDE
Waveforms
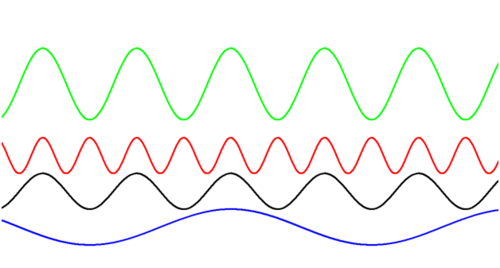
LARGEST AMPLITUDE?
SMALLEST FREQUENCY?
SMALLEST PERIOD?
SAME OR DIFFERENT PHASE?
The Ultimate Sine Recipe
y = sin(angle * frequency + phase) * amplitude;-
ANGLE = input angle (in radians)
-
FREQUENCY = how often the wave repeats
-
PHASE = starting point of wave
-
AMPLITUDE = wave range

Exercise 1C: Complete sine animation
Waveform and Cosine
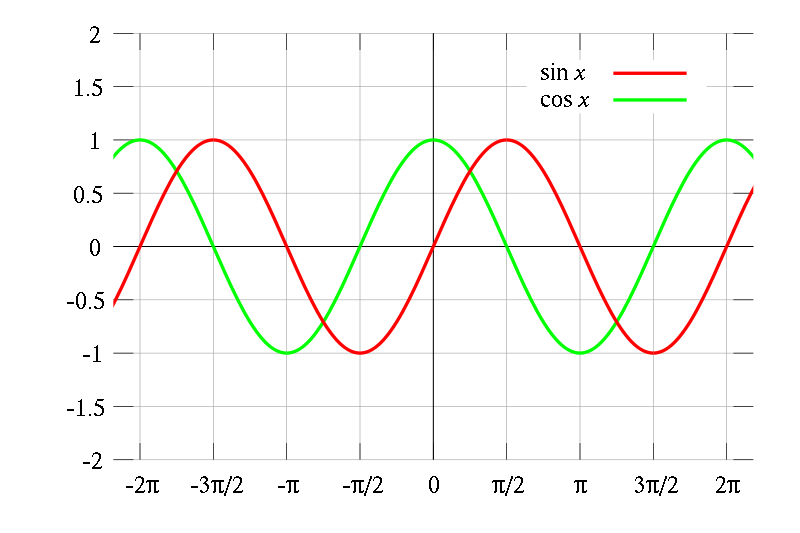

SIN
COS
COSINE IS JUST SINE WITH DIFFERENT PHASE!
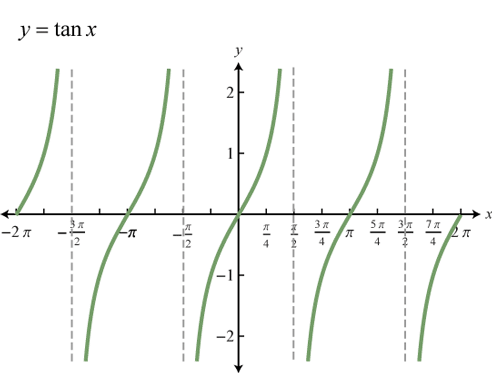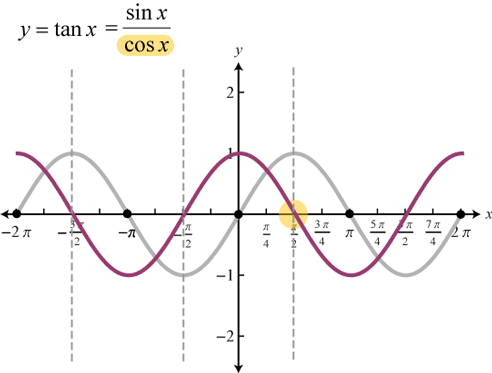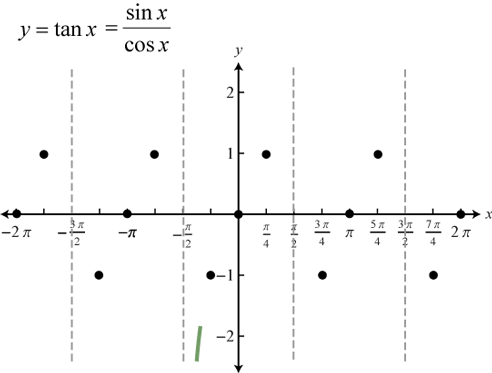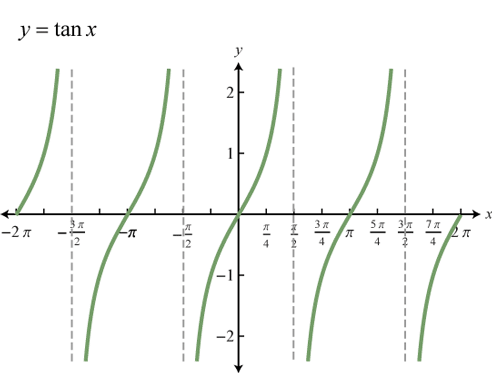
Tangent
-
TANGENT FUNCTION tan(θ) gets values between -∞ and ∞
-
More useful is the inverse tangent function atan2()
-
Calculates the angle between the origin an a point
-
Used for orienting shapes to the position of the cursor
-
Exercise 2A: Waveform
VARIATION: Exercise 2B: Waveforms
- Draw the waveform using different shapes, eg. rect()!
- Try using beginShape() endShape() and vertex()!
Modulation
-
You can modulate the parameters of a sine wave with another sine wave!
-
FREQUENCY MODULATION
-
The frequency of the wave changes with another sine function
-
-
AMPLITUDE MODULATION
-
The amplitude of the wave changes with another sine function
-
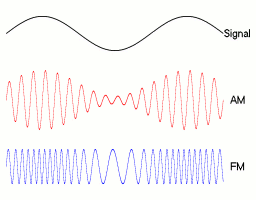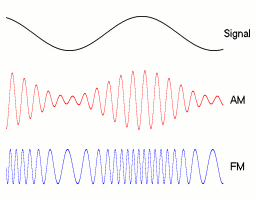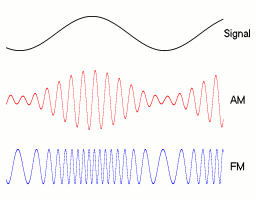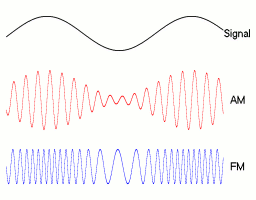
//frequency oscillates between values 2 and 4
let frequency = map(sin(angle2), -1, 1, 2, 4);
//amplitude oscillates between values 100 and 200
let amplitude = map(sin(angle3), -1, 1, 100, 200);
y = sin(angle1 * frequency + phase) * amplitude;Exercise 3A: Modulation
VARIATION: Exercise 3B:
Multiple modulations
-
Draw multiple waveforms using a nested loop!
-
Create another variable ySpacing. Set it to be 2 * x-spacing
-
Add another for-loop outside the first loop:
-
Loop through y-coordinates from top to bottom of the canvas. Extend the waves 100px outside the canvas.
-
Increment with ySpacing
-
-
Calculate the displacement (let dy) for each rect from the original y-coordinate:
- add the wave function to the y-coordinate of each wave
- Draw rect at coordinates (x,dy), the size of xSpacing
Additive synthesis
-
Adding two sine waves together creates a waveform within a waveform
//create first waveform
let wave1 = sin(input*frequency1+phase1)*amplitude1;
//create second waveform
let wave2 = sin(input*frequency2+phase2)*amplitude2;
//add the waves together
let y = wave1 + wave2;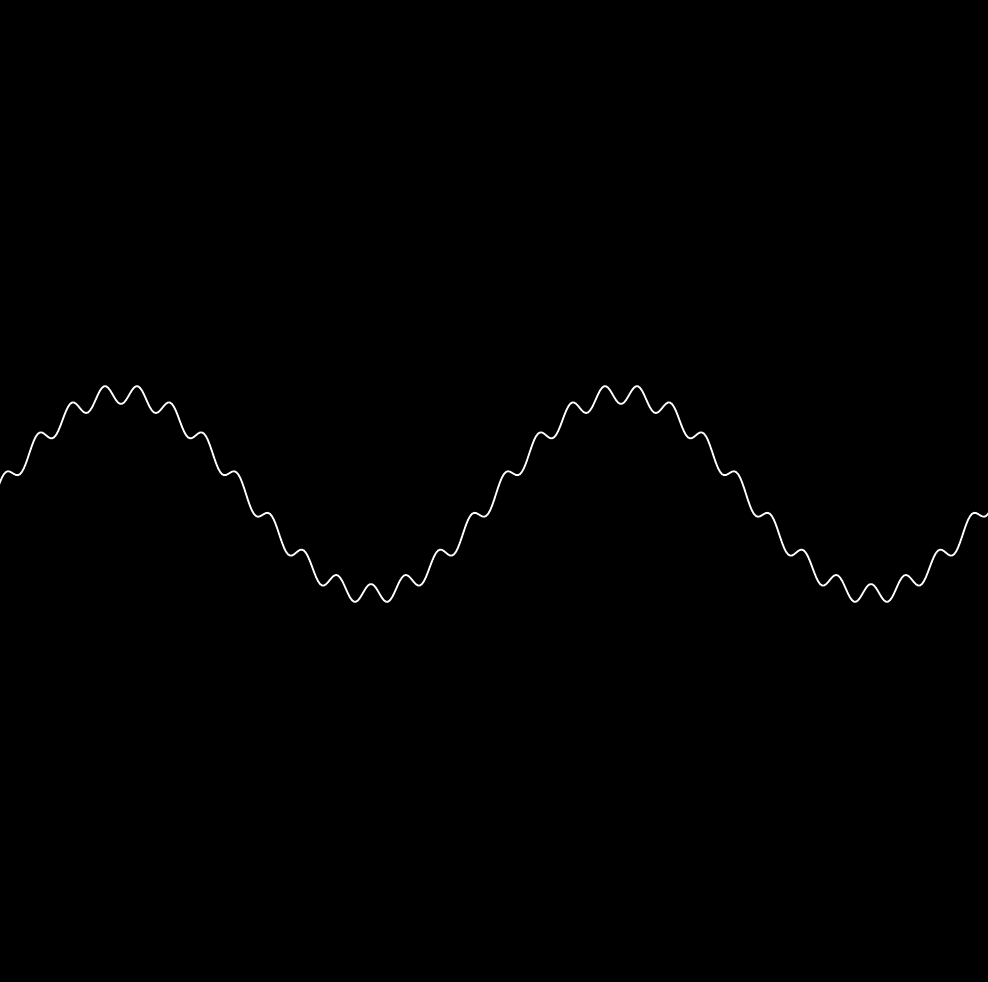
Polar coordinates
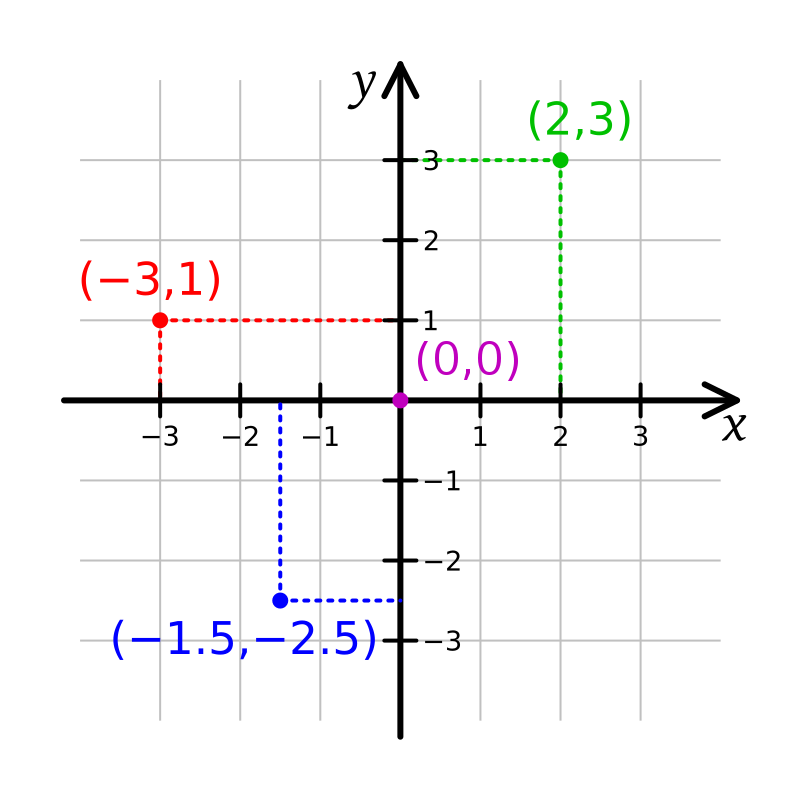
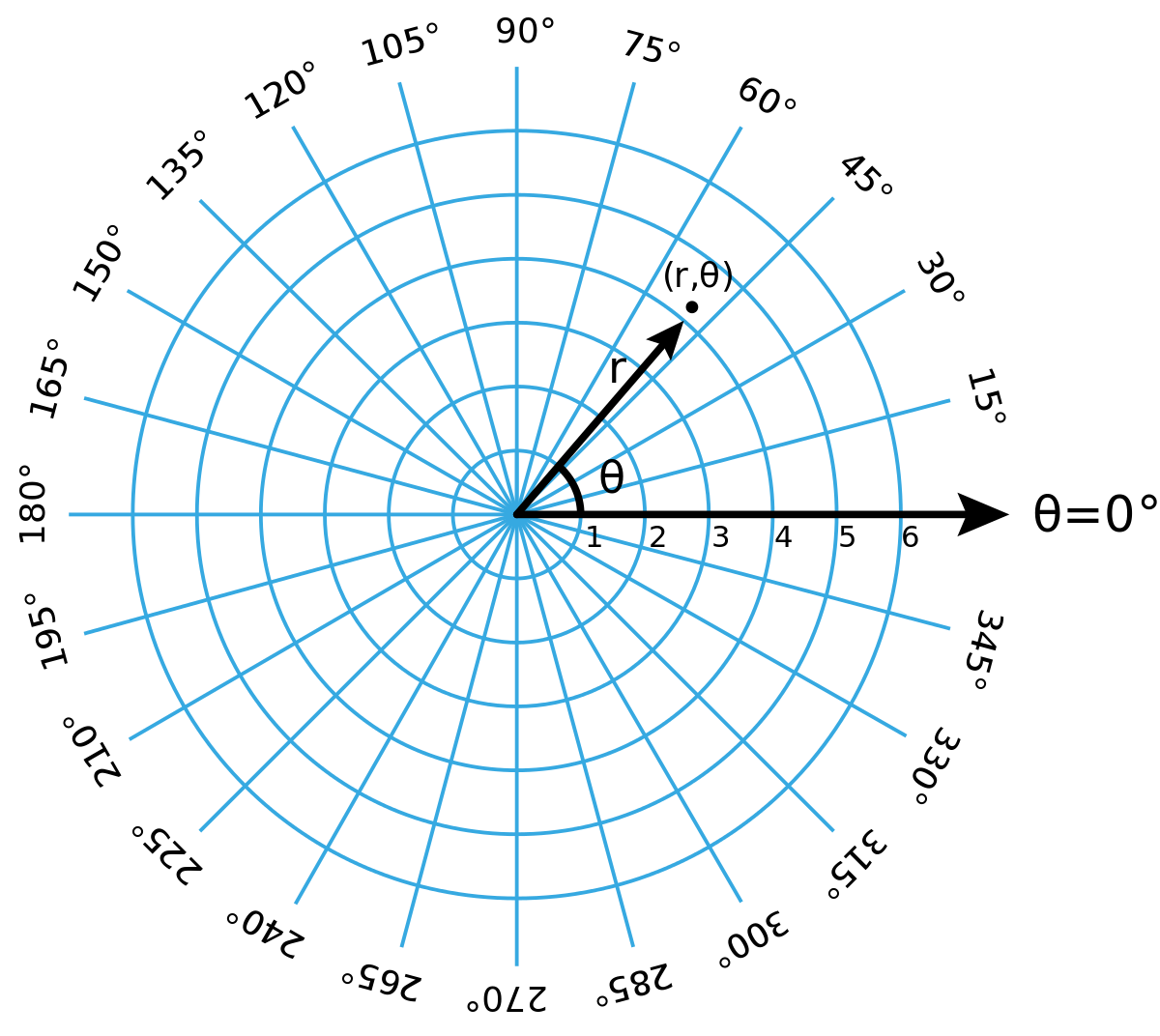
CARTESIAN COORDINATES
POLAR COORDINATES
- x and y coordinates
- radius r and angle θ
Polar to cartesian
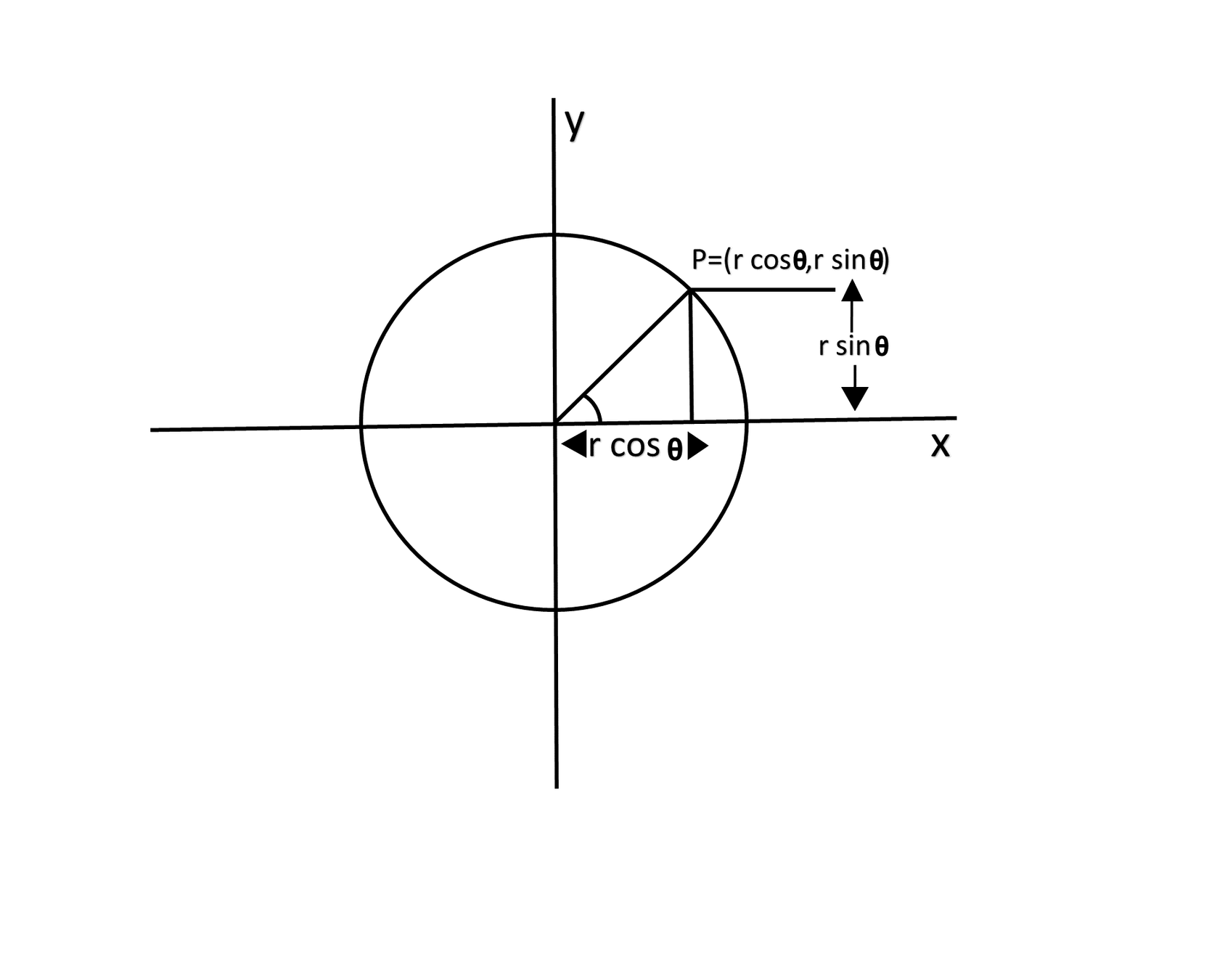

- Right angle triangle inside a circle:
- From the radius r and the angle θ we can calculate coordinates x and y on the circle
Polar to cartesian
CALCULATING COORDINATES ON A CIRCLE USING ANGLE AND RADIUS
let y = sin(angle)*r;
let x = cos(angle)*r;RADIUS
ANGLE
POINT (X,Y)
Exercise 5: Polar coordinates
- Draw multiple different geometric shapes using polar coordinates!
Polar coordinates
WE CAN DRAW VARIOUS GEOMETRIC SHAPES WITH SIMPLE TRIGONOMETRIC FORMULAS!
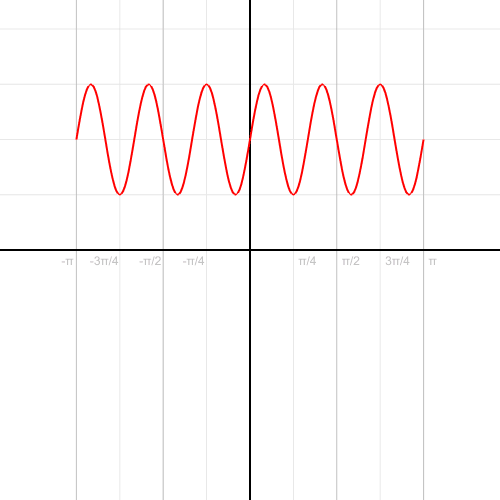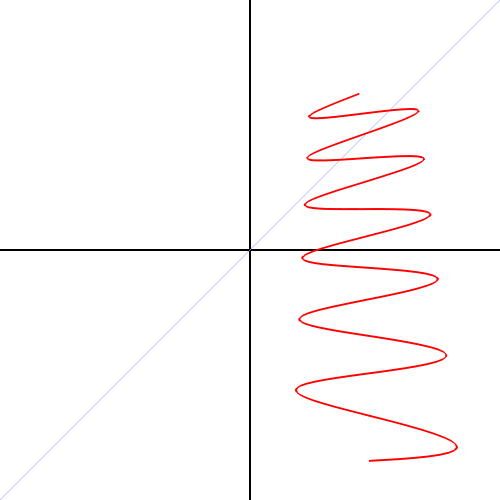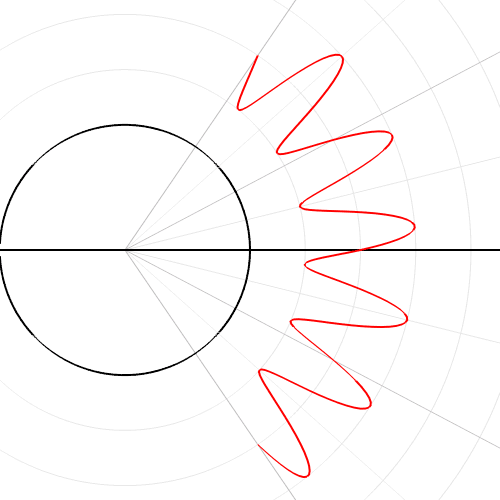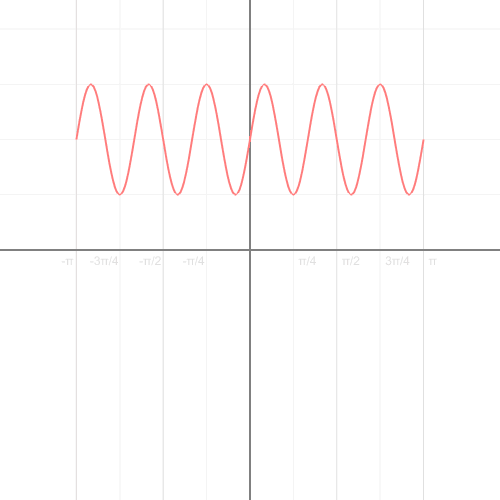
Exercise 5b: Polar coordinates flower
VARIATION:
- Modulate the radius of the shape using a sine wave!
Exercise 6: Polar exploration


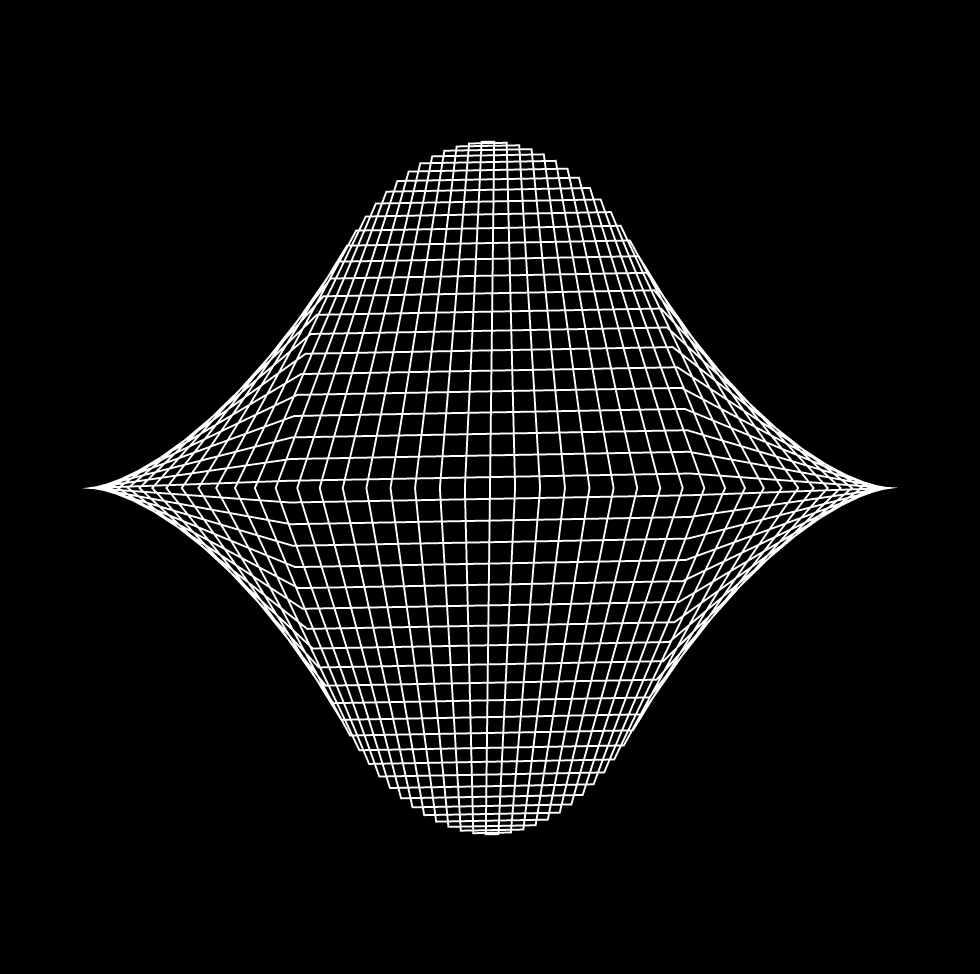


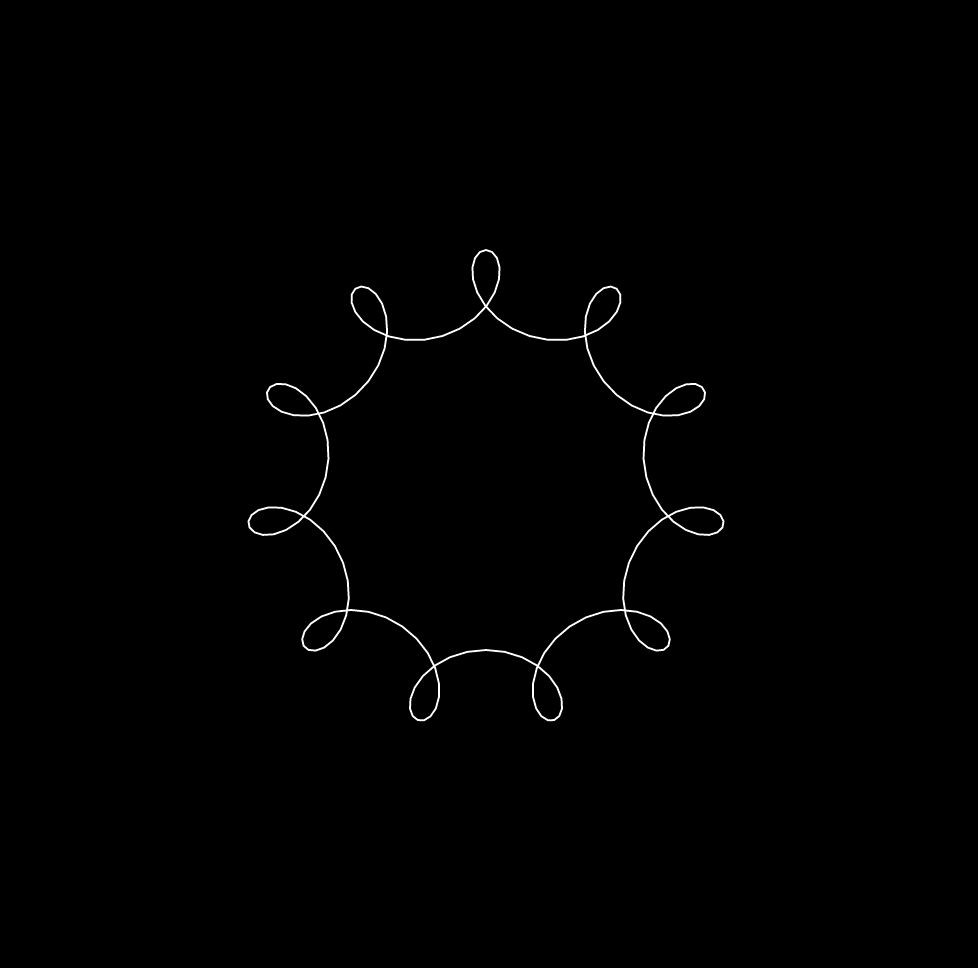
VARIATIONS
Noise
- The noise function is in many ways similar to sine function and random function
- Input value should be a linear sequence
- Always returns a value between 0 and 1
- Produces a harmonically changing random sequence
- Uses the Perlin noise algorithm developed by Ken Perlin 1983
noise(x, [y], [z])Recap
//trigonometric functions
sin(angle);
cos(angle);
tan(angle);
//inverse tangent
atan2(x,y);
//sine equation
let y = sin(angle * frequency + phase) * amplitude;
//polar to cartesian coordinates
let y = sin(angle)*rad;
let x = cos(angle)*rad;
//noise produces a harmonic sequence of random values
noise(x,[y]);
Coding Assignment IV:
Alien Language
Coding Assignment IV
Alien Language
- Visualise a fragment of a previously unknown language
- You don't have to create a complete writing system or alphabet!
- What could a completely alien form of writing look like?
- What does it say about the culture that produced it?
- Is there a way to interpret the semantic content, or is the logic and meaning unintelligible to us?

Manfred Mohr (1979) P-049 Formal Language, IRI = 2
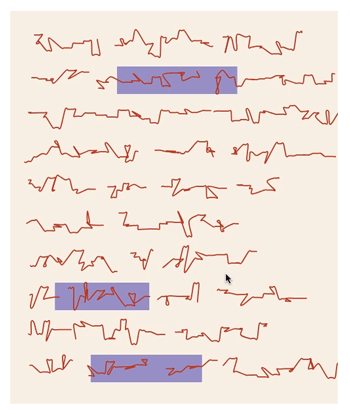
Beverly Chou (2018) Asemic writing


Gail Tarantino (2015) From Dim to Bright-Henrietta
NEW ALPHABET?
ASEMIC WRITING?
ENCRYPTED MESSAGE?
UNKNOWN GLYPHS?
ALTERNATIVE VISUALISATION OF TEXT?
WHAT CONSTITUTES A LANGUAGE?

Arecibo message (1974)
Moon runes by J.R.R. Tolkien
PICTOGRAMS?
Coding Assignment IV: CONSTRAINTS
- There are no constraints!
- You can use any or every computational method we have learned on the course.
- It's up to you to decide what could constitute as a language for an alien culture or life form.
TIPS
- This is your last weekly coding assignment on the course! Make it count :)
Coding Assignment IV: INSTRUCTIONS
-
Comment your code well!
-
Add your name and date in the comments in the beginning of the sketch
-
Use comments to explain how the code works
-
Briefly in the beginning of the sketch
-
Inline comments in more detail
-
-
Reference any borrowed code (include links)
-
Explain which parts you have borrowed and how have you modified them
-
(No need to reference exercises from class)
-
- Explain (briefly) the key features about the alien writing system and the culture that produced it
-
-
Submit a link in MyCourses by next Tuesday
To do
- Coding Assignment IV
- Weekly reading IV
