Deep Probabilistic Learning
Capturing Uncertainties with Deep Neural Networks

MML – Cours 11, Friday April 9th 2021   

Francois Lanusse @EiffL

+ p(x) =

Follow the slides live at 

 

https://slides.com/eiffl/mml/live

Outline for this session

  • Modeling aleatoric uncertainties
    • Conditional Density Estimators
    • Likelihood-Free Inference with Neural Posterior Estimators
       
  • Modeling epistemic uncertainties
    • Bayesian Neural Networks
    • Out of Distribution estimation

Before we dive in...

What uncertainties are we talking about?

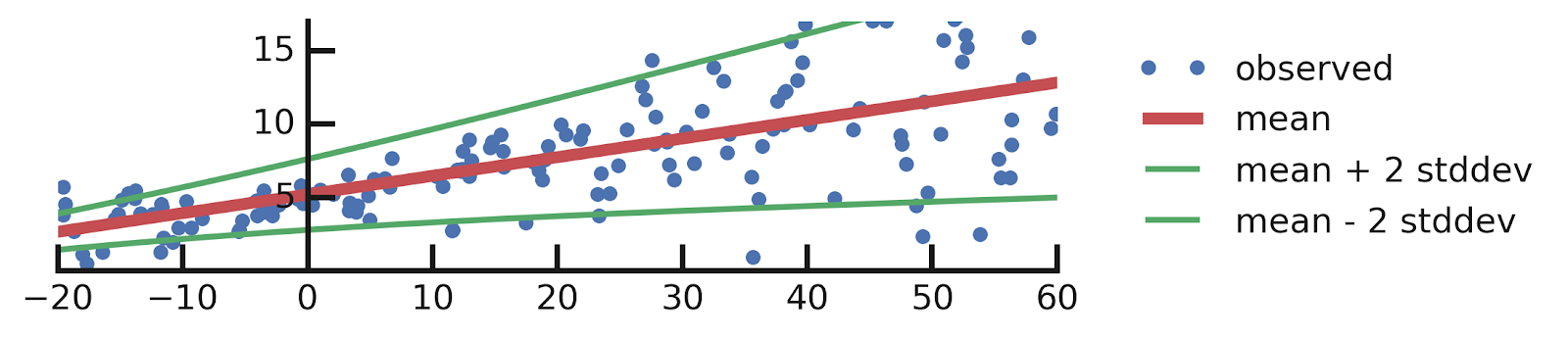
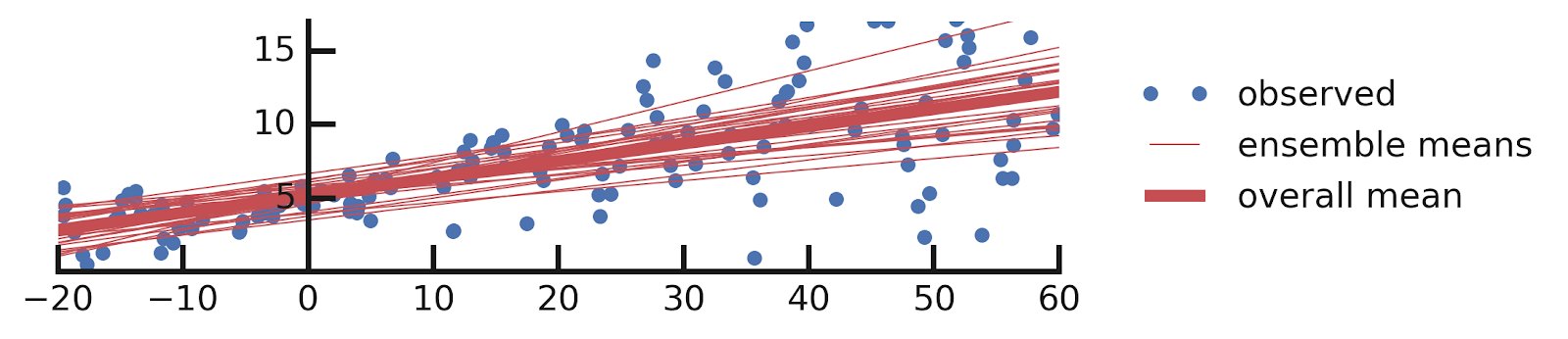
A Motivating Example: Probabilistic Linear Regression

From this excellent tutorial: 

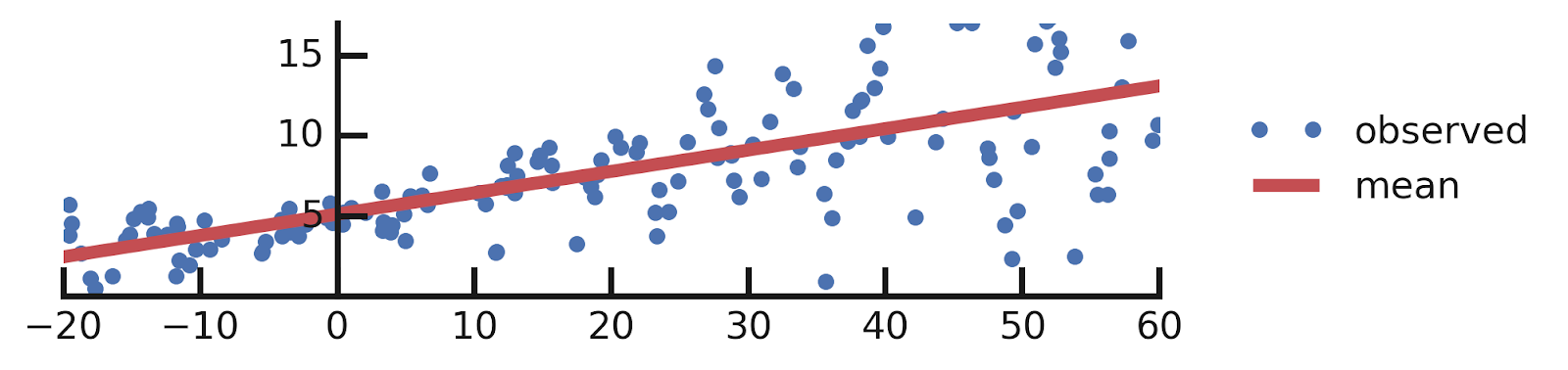
  • Linear regression

     
  • Aleatoric Uncertainties

     
  • Epistemic Uncertainties

     
  • Epistemic+ Aleatoric Uncertainties
\hat{y} = a x
\hat{y} \sim \mathcal{N}(a x, \sigma^2)
\hat{y} = w x \quad w \sim p(w | \{x_i, y_i\})
\hat{y} \sim \mathcal{N}(w x, \sigma^2) \\ w, \sigma \sim p(w, \sigma | \{x_i, y_i\})

Modeling Aleatoric Uncertainties

Let us consider a toy example

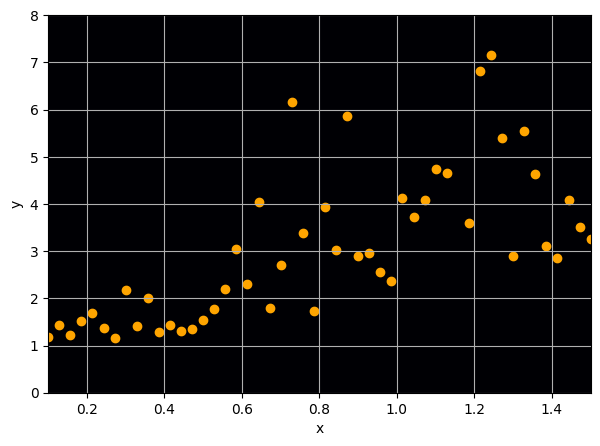
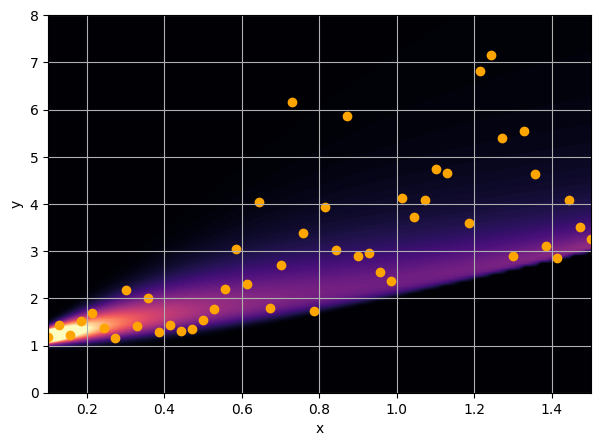
There are intrinsic uncertainties in this problem, at each x there is a full

  • Option 1) Train a neural network to learn a function                      under an MSE loss:

     
  • Option 2) Train a neural network to learn a function                      under an l1 loss:

     
  • Option 3) Train a neural network to learn a distribution                 using a Maximum Likelihood  loss

 

\hat{y} = f_\varphi(x)
\mathcal{L} = \parallel y - f_\varphi(x) \parallel_2^2
p(y | x)

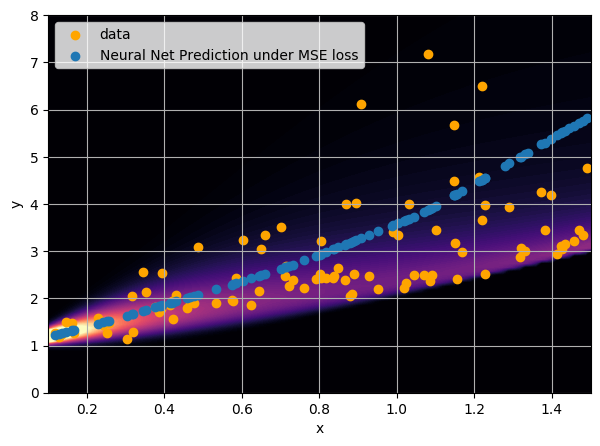
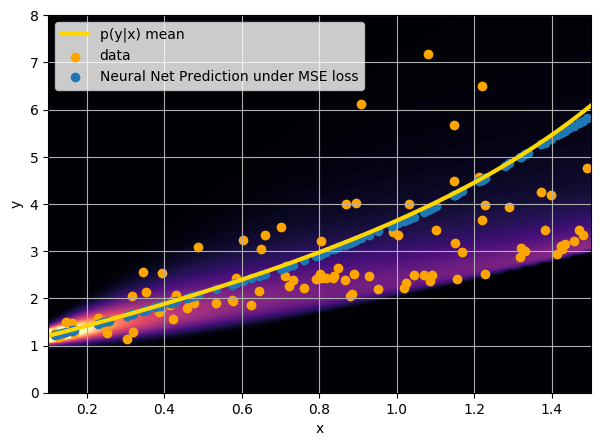
I have a set of data points {x, y} where I observe x and want to predict y.

\hat{y} = f_\varphi(x)
\mathcal{L} = | y - f_\varphi(x) |
p_\varphi(y | x)
\mathcal{L} = - \log p_\varphi(y | x )

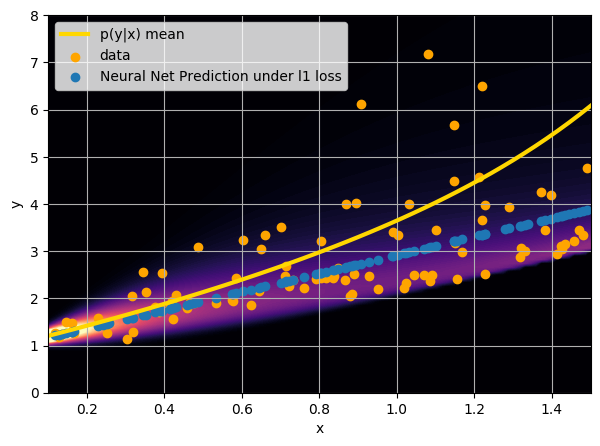
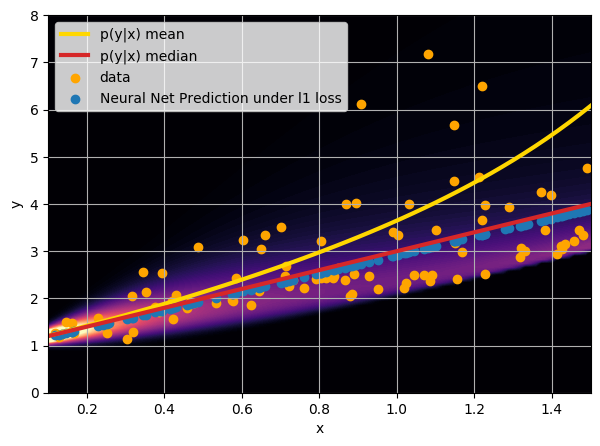
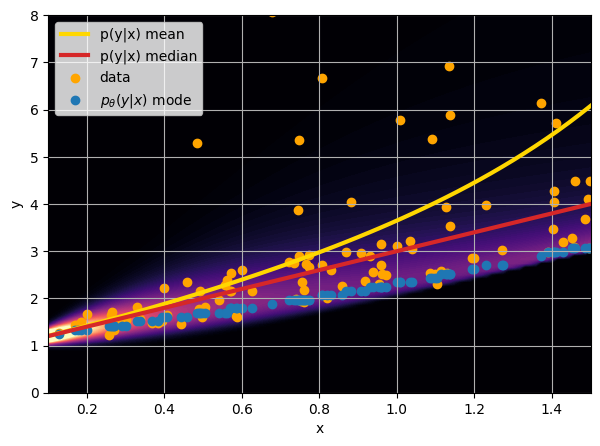
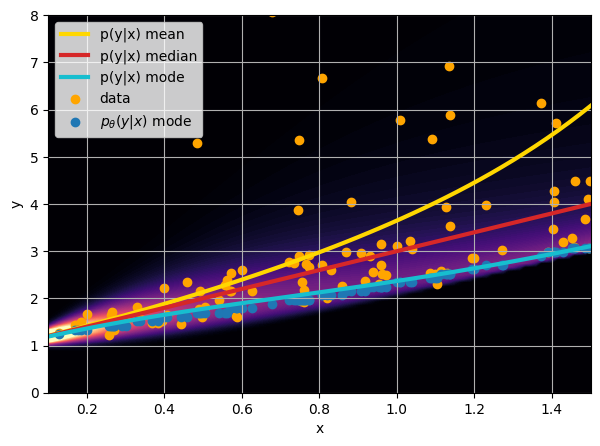
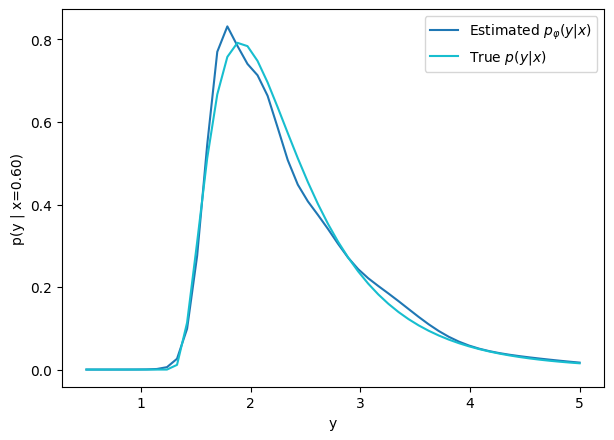
How did we do this?

Step 1: Conditional Neural Density Estimators
 

We need a parametric conditional distribution to
compute  

\log p_\varphi(y | x)
p_\varphi(y | x) = \sum_{i=1}^K \pi_i \mathcal{N}( \mu_\varphi(x), \Sigma_\varphi(x))
p_\varphi(y | x) = \Pi_{d=1}^D p_\varphi(y_d | y_1, \ldots, y_{d-1}, x)
p_\varphi(y | x) = p(z = f_\varphi(y, x)) \left| \det \frac{\partial f_\varphi}{\partial z} \right|

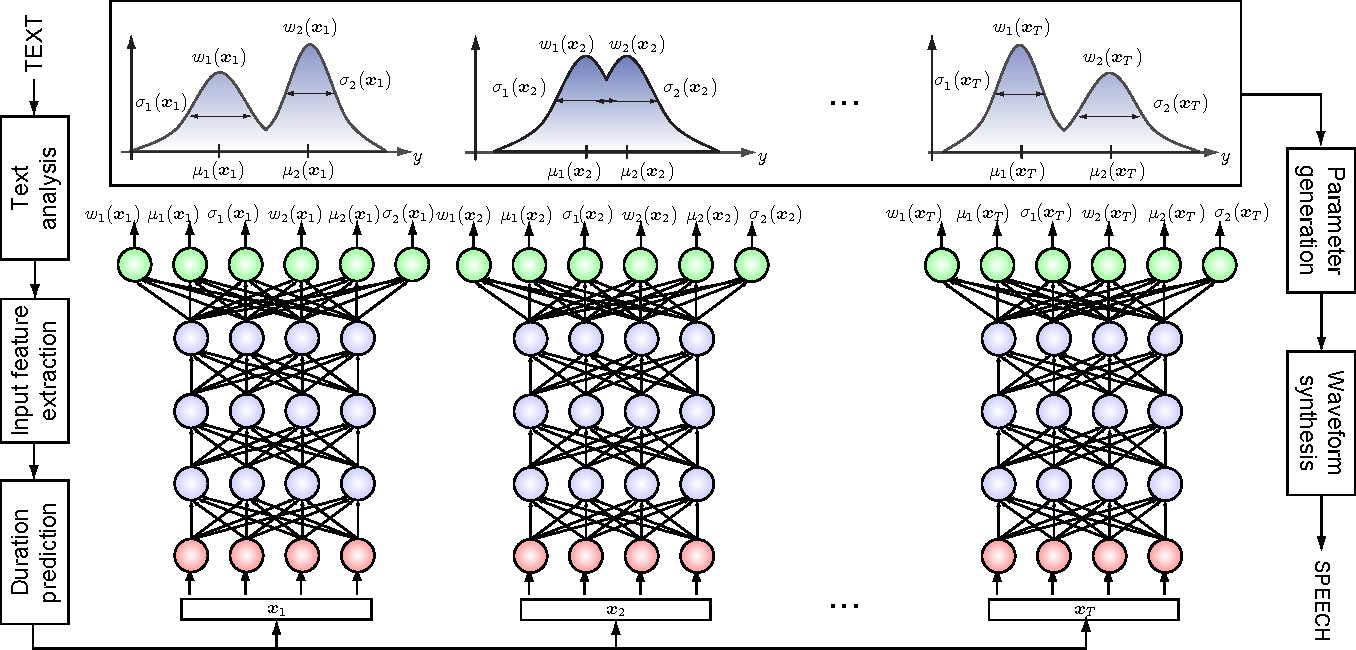
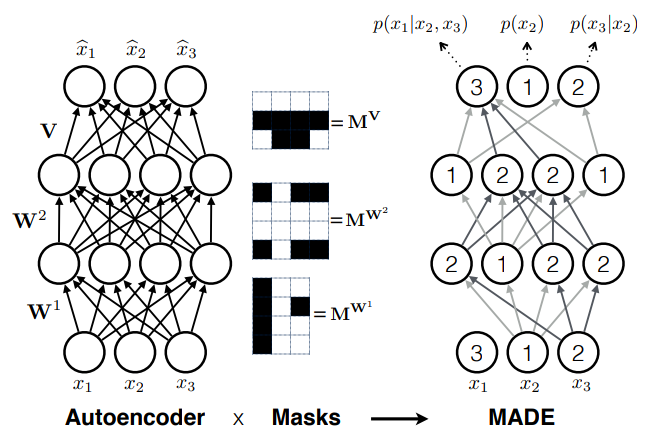
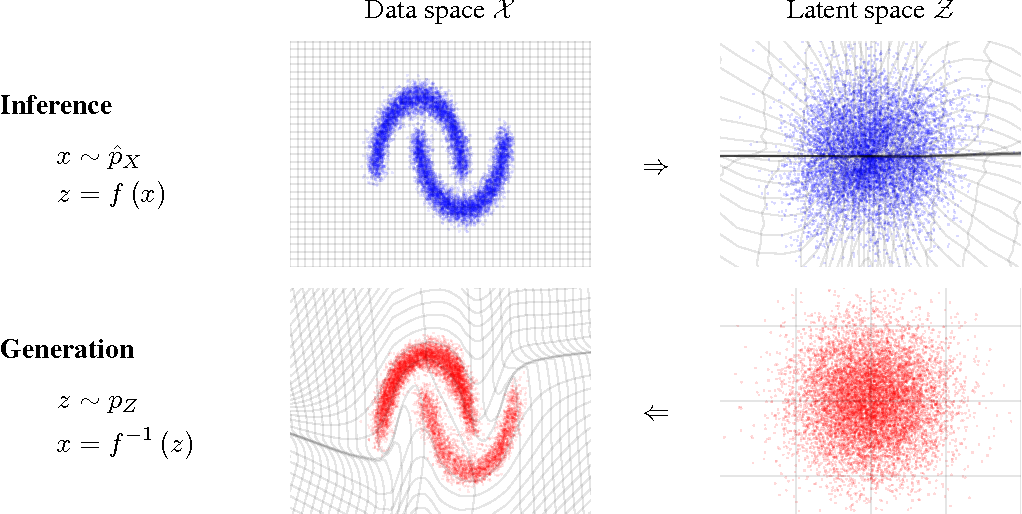
How do we fit this conditional distribution?

A distance between distributions: the Kullback-Leibler Divergence

credit

D_{KL} (p || q) = \mathbb{E}_{x \sim p(x)} \left[ \log \frac{p(x)}{q(x)} \right]

Step 2: We need a tool to compare distributions

D_{KL} \left( p(x, y) || p_\varphi(y| x) p(x) \right) = - \mathbb{E}_{p(x,y)} \left[ \log \frac{ p_\varphi(y | x) p(x) }{ p(x) p(y | x) } \right]
= - \mathbb{E}_{p(x, y)} \left[ \log p_\varphi(y | x) \right] + cst

Minimizing this KL divergence is equivalent to minimizing the negative log likelihood of the model

D_{KL} \left( p(x, y) || p_\varphi(y | x) p(x) \right) = 0 \\ <=> \\ p_\varphi(y | x) \propto p(y | x)

How do we do this in practice?

Tensorflow Probability

import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions

# Build model.
model = tf.keras.Sequential([
  tf.keras.layers.Dense(1+1),
  tfp.layers.IndependentNormal(1),
])

# Define the loss function:
negloglik = lambda x, q: - q.log_prob(x)

# Do inference.
model.compile(optimizer='adam', loss=negloglik)
model.fit(x, y, epochs=500)

# Make predictions.
yhat = model(x_tst)

Try it out with this notebook

A Concrete Example: Estimating Masses of Galaxy Clusters

Try it out at this notebook

We  want to make dynamical mass measurements using information from member galaxy velocity dispersion and about the radial distance distribution (see Ho et al. 2019).

First attempt with an MSE loss

regression_model = keras.Sequential([
    keras.layers.Dense(units=128, activation='relu', input_shape=(14,)),
    keras.layers.Dense(units=128, activation='relu'),
    keras.layers.Dense(units=64, activation='tanh'),
    keras.layers.Dense(units=1)
])

regression_model.compile(loss='mean_squared_error', optimizer='adam')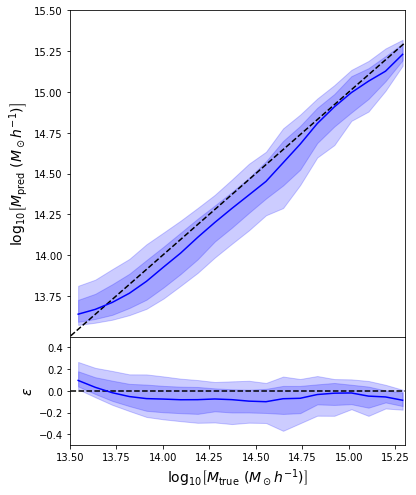
  • Simple Dense network  using 14 features derived from galaxy positions and velocity information
     
  • We see that the predictions are biased compared to the true value of the mass... Not good.

Second attempt: Probabilistic Modeling

num_components = 16
event_shape = [1]

model = keras.Sequential([
    keras.layers.Dense(units=128, activation='relu', input_shape=(14,)),
    keras.layers.Dense(units=128, activation='relu'),
    keras.layers.Dense(units=64, activation='tanh'),
    keras.layers.Dense(tfp.layers.MixtureNormal.params_size(num_components, event_shape)),
    tfp.layers.MixtureNormal(num_components, event_shape)
    ])

negloglik = lambda y, p_y: -p_y.log_prob(y)

model.compile(loss=negloglik, optimizer='adam')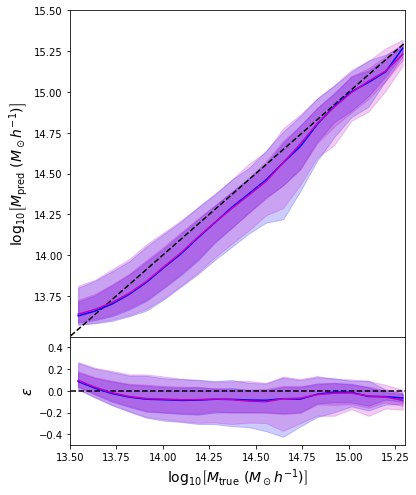
  • Same Dense network but now using a Mixture Density output.
     
  • Using the mean of the predicted distribution as our mass estimate: We see the exact same behaviour
    What am I doing wrong???
q_\varphi(\theta= \mathrm{cat} | x) = 0.9
x

credit: Venkatesh Tata

 

Let's start with binary classification

\theta

=> This means expressing a posterior as a Bernoulli distribution with parameter predicted by a neural network

p(\theta | x) \propto p(x | \theta) p(\theta)

How do we adjust this parametric distribution to match the true posterior ?

Step 1: We neeed  some data

\mathcal{D} = \{ (x_i, \theta_i) \}_{i \in [0, N]}

cat or dog image

label 1 for cat, 0 for dog

(x, \theta) \sim p(x, \theta) = \tilde{p}(\theta) p(x | \theta)

Probability of including cats and dogs in my dataset

Google Image search results for cats and dogs

D_{KL} \left( p(x, \theta) || q_\varphi(\theta | x) \tilde{p}(x) \right) = - \mathbb{E}_{p(x,\theta)} \left[ \log \frac{ q_\varphi(\theta | x) \tilde{p}(x) }{ \tilde{p}(\theta) p(x | \theta) } \right]
= - \mathbb{E}_{p(x, \theta)} \left[ \log q_\varphi(\theta | x) \right] + cst

Minimizing this KL divergence is equivalent to minimizing the negative log likelihood of the model

D_{KL} \left( p(x, \theta) || q_\varphi(\theta | x) \tilde{p}(x) \right) = 0 \ <=> \ q_\varphi(\theta | x) \propto \frac{\tilde{p}(\theta)}{p(\theta)} p(\theta | x)

At minimum negative log likelihood, up to a prior term, the model recovers the Bayesian posterior

p(\theta | x) \propto p(x | \theta) p(\theta)

with

How do we adjust this parametric distribution to match the true posterior ?

In our case of binary classification:

\mathbb{E}_{p(x,\theta)}[ - \log q_\varphi(\theta | x)] =\\ \frac{1}{N} \sum_{i=1}^{N} p(1|x_i) \log q_\varphi(1 | x_i) + (1-p(1|x_i)) \log q_\varphi(1 | x_i)

We recover the binary cross entropy loss function !

The Probabilistic Deep Learning Recipe for Neural Posterior Estimation

  • Express the output of the model as a distribution


     
  • Optimize for the negative log likelihood


     
  • Maybe adjust by a ratio of proposal to prior if the training set is not distributed according to the prior

     
  • Profit!
q_\varphi(\theta | x)
\mathcal{L} = - \log q_\varphi(\theta | x)
q_\varphi(\theta | x) \propto \frac{\tilde{p}(\theta)}{p(\theta)} p(\theta | x)

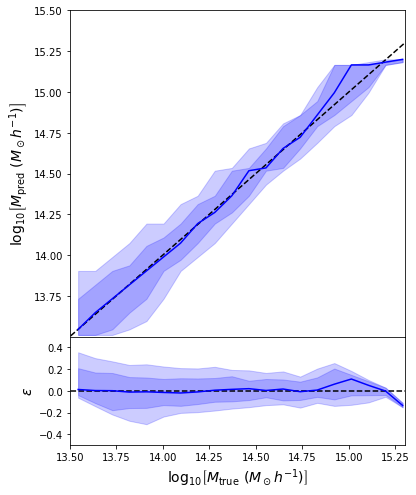
Back to our Dynamical Mass Predictions

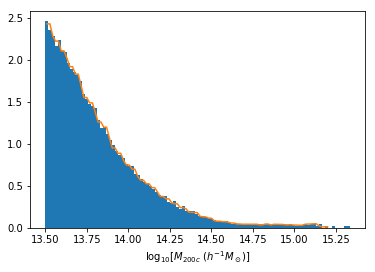
Distribution of masses in our training data

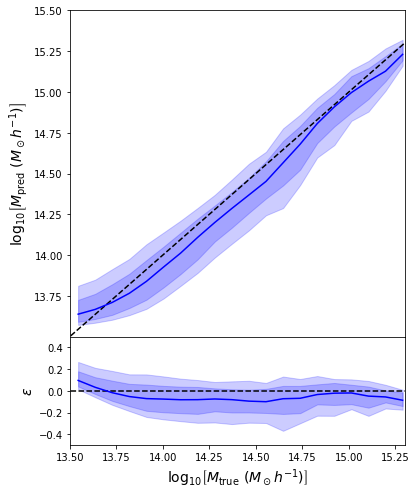
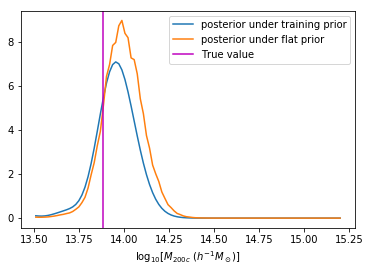
q(M_{200c} | x ) \propto \frac{\tilde{p}(M_{200c})}{p(M_{200c})} p(M_{200c} | x)

We can reweight the predictions for a desired prior

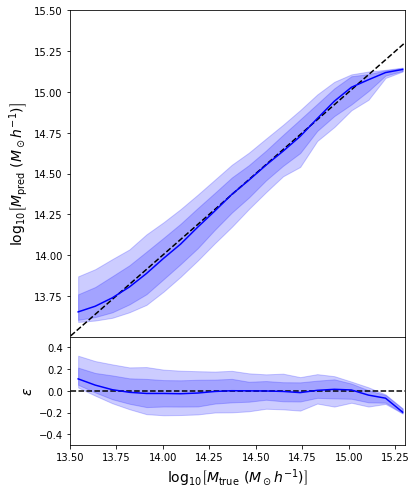
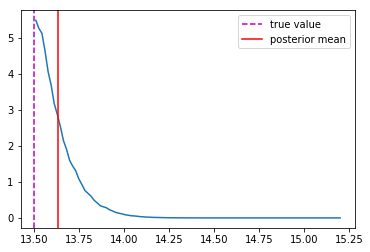
Last detail, use the mode instead of the mean posterior

Takeaway Message

  • Using a model that outputs distributions instead of scalars is always better!

     
  • It's 2 lines of TensorFlow Probability

     
  • Careful about interpreting these distributions as a Bayesian posterior, the training set acts as an Interim Prior, not necessarily matching your Bayesian prior.

Modeling Epistemic Uncertainties

A Quick reminder

From this excellent tutorial: 

  • Linear regression

     
  • Aleatoric Uncertainties

     
  • Epistemic Uncertainties

     
  • Epistemic+ Aleatoric Uncertainties
\hat{y} = a x
\hat{y} \sim \mathcal{N}(a x, \sigma^2)
\hat{y} = w x \quad w \sim p(w | \{x_i, y_i\})
\hat{y} \sim \mathcal{N}(w x, \sigma^2) \\ w, \sigma \sim p(w, \sigma | \{x_i, y_i\})

The idea behind Bayesian Neural Networks

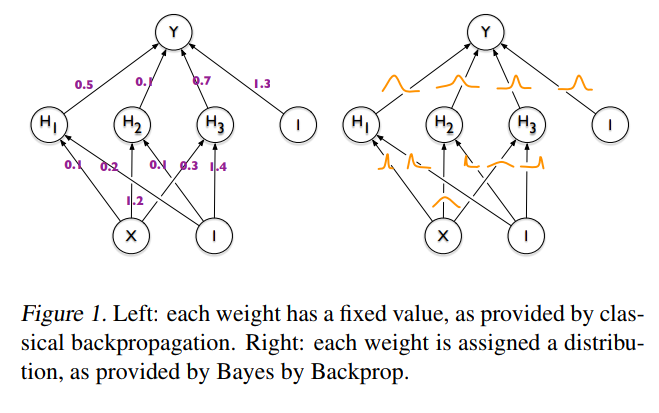
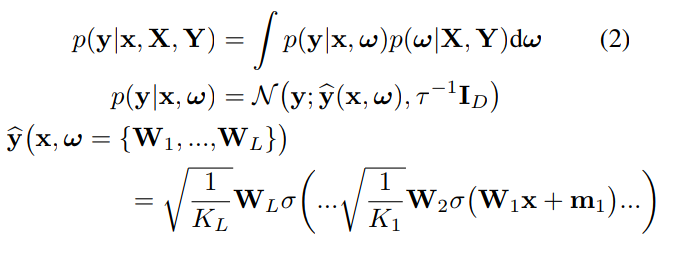
Given a training set  D = {X,Y}, the predictions from a Neural Network can be  expressed as:

Weight Estimation by Maximum Likelihood

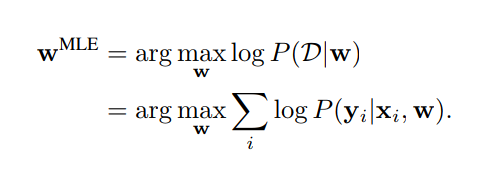
Weight Estimation by Variational Inference

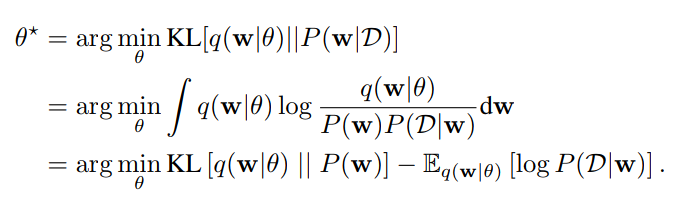
A first approach to BNNs:
Bayes by Backprop (Blundel et al. 2015)

  • Step 1: Assume a variational distribution for the weights of the Neural Network


     
  • Step 2: Assume a prior distribution for these weights


     
  • Step 3: Learn the parameters  of the variational distribution by minimizing the ELBO

 

 

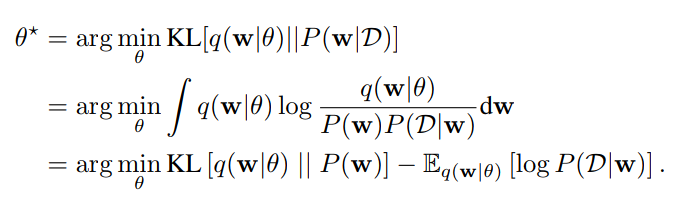
q_\theta(w) = \mathcal{N}( \mu_\theta, \Sigma_\theta )
p(w) = \mathcal{N}(0, I)

What happens in practice

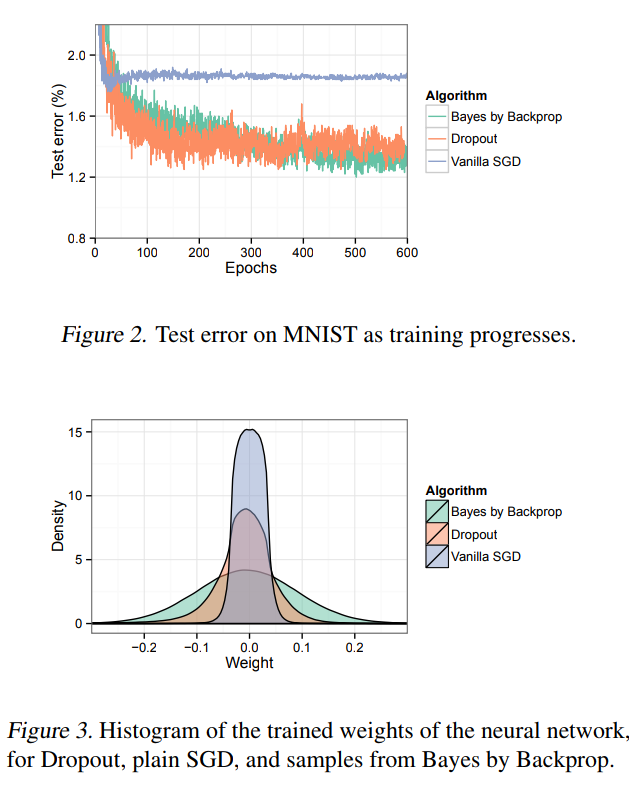
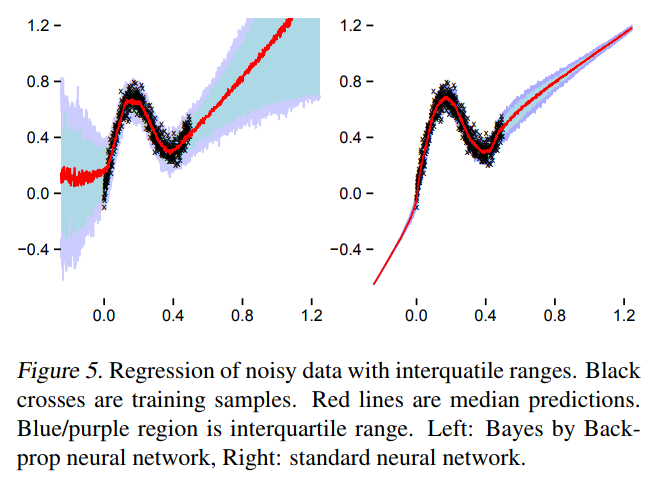
TensorFlow Probability implementation

A different approach:
Dropout as a Bayesian Approximation (Gal & Ghahramani, 2015)

Quick reminder on dropout
 

Hinton 2012, Srivastava 2014

Variational Distribution of Weights under Dropout

  • Step 1: Assume a Variational Distribution for the weights



     
  • Step 2: Assume a Gaussian prior for the weights, with "length scale" l
     
  • Step 3: Fit the parameters of the variational distribution by optimizing the ELBO

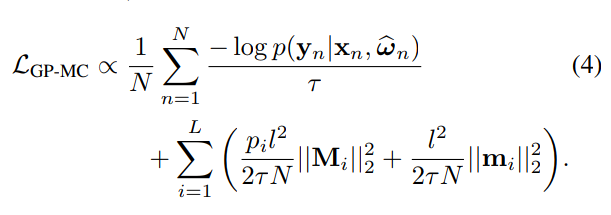
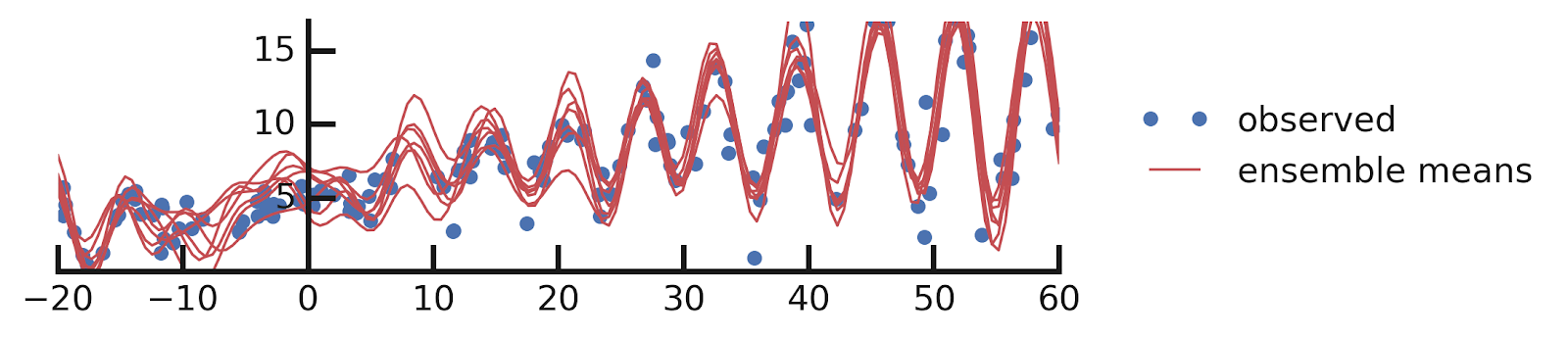
Example

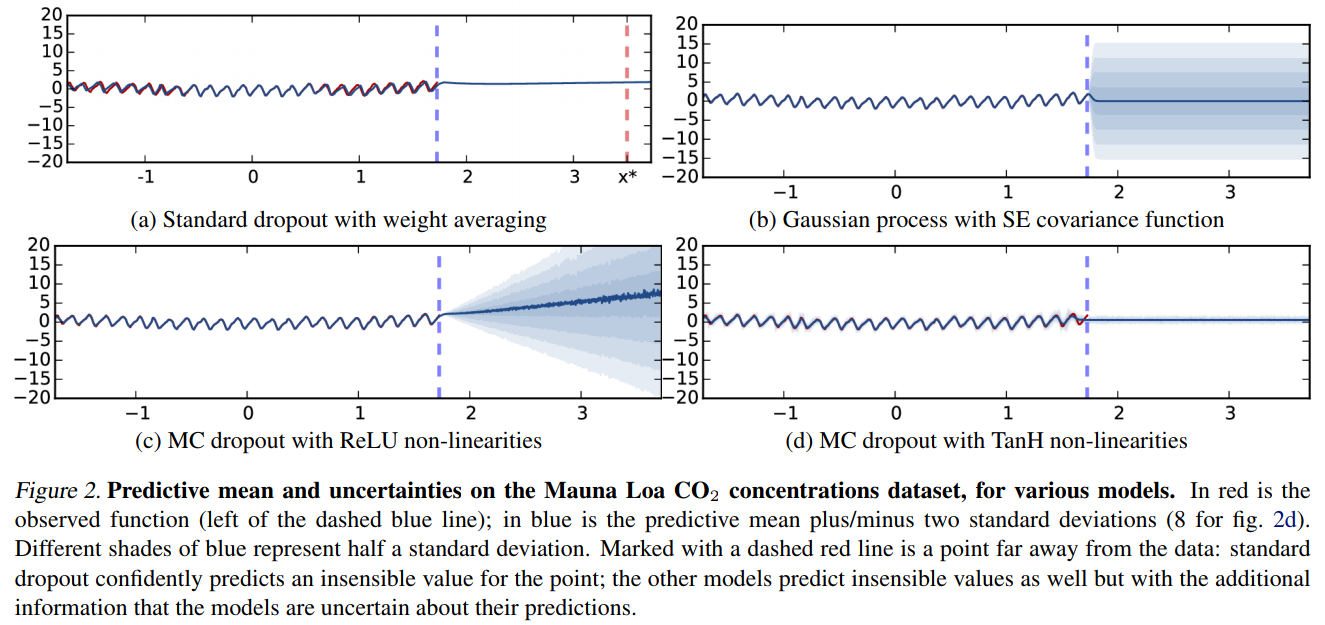
These are not the only methods

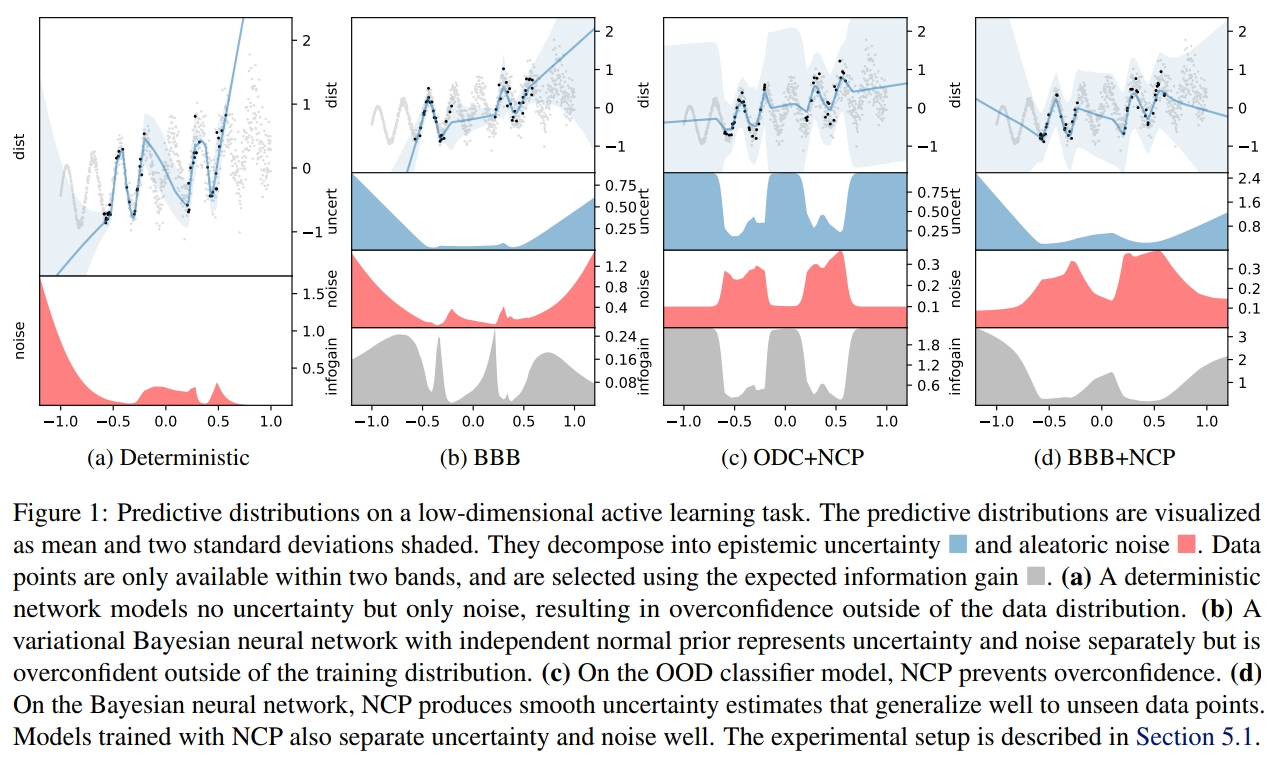
Takeaway message on Bayesian Neural Networks

  • They give a practical way to model epistemic uncertainties, aka unknowns unknows, aka errors on errors
     
  • Be very careful when interpreting their output distributions, they are Bayesian posterior, yes, but under what priors?






     
  • Having access to model uncertainties can be used for active sampling

Putting it all together

https://arxiv.org/pdf/1905.07424.pdf