Safe Reinforcement Learning

Elena Smirnova

Joint work with Elvis Dohmatob and Jeremie Mary

Introduction to RL

Environment

Agent

Action

Next state

Reward

Current state

How to learn safely?

Environment is unknown!

Learn safely under uncertainty

Prepare for the worst case

But not too conservative!

?

Overview

Safety w.r.t. finite amount of experience

Approximation for continuous action space

Safety + SOTA!

SOTA

Adversarial Bellman operator

Dynamic Programming

Introduction to RL

Markov Decision Process

$$M := (\mathcal{S}, \mathcal{A}, P, r, \gamma)$$

  • state space \(\mathcal{S}\)
  • action space \(\mathcal{A}\)
  • transition matrix \(\left(P(s'|s,a)\right)_{s,s' \in \mathcal{S}, a \in \mathcal{A}}\): probability of moving to state \(s'\) given action \(a\) in state \(s\)
  • reward \(r(s,a)\), bounded
  • discount factor \(\gamma \in [0,1)\)

Policy and Value

Policy \( \pi: \mathcal{S} \rightarrow \Delta_\mathcal{A}\)

Value function \( V: \mathcal{S} \rightarrow \mathbb{R} \)

V^\pi(s) = \mathbb{E}_{a_t \sim \pi(\cdot|s_t), s_{t+1} \sim P(\cdot|s_t, a_t)} [ \sum_{t=0}^{\infty} \gamma^t r(s_t,a_t) | s_0=s]

How to act in a state

How good is a state

\(\pi(a|s)\) is a probability of chosing action \(a\) in state \(s\)

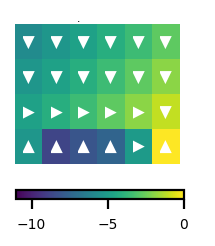
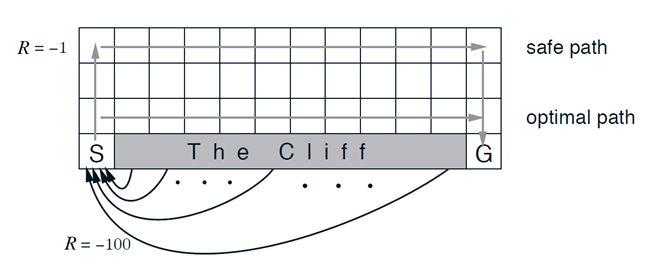
Cliff walking

MDP

Policy and Value

RL objective

Maximize value at each state

\pi^* \in \argmax_{\pi} V^\pi
V^* = \max_{\pi} V^\pi

RL algorithms

Dynamic Programming

Policy Gradient

Bellman operator

Policy and Value Iteration

SOTA: Actor-Critic algorithms

Policy Gradient Theorem

REINFORCE

SOTA: Trust Region Policy Optimization

Dynamic programming

Bellman operator \( \mathcal{T}^\pi: V \rightarrow V\)

[\mathcal{T}^\pi V](s) := \langle Q_V(s, \cdot), \pi(\cdot|s) \rangle

Bellman equation

V^\pi(s) = \mathbb{E}_{a \sim \pi(\cdot|s)} [r(s,a) + \gamma \mathbb{E}_{s' \sim p(s'|s,a)} V^{\pi}(s')]
= \langle Q_{V^\pi}(s, \cdot), \pi(\cdot|s) \rangle
Q_{V^\pi}(s,a)

Q-value of an action * how often this action is taken

Bellman operator

Fixed point

\mathcal{T}^\pi V^\pi = V^\pi

Exists and unique

\(\gamma\)-contraction

\|\mathcal{T}^\pi V_1 - \mathcal{T}^\pi V_2\|_\infty \le \gamma \|V_1 - V_2\|_\infty

Useful to show convergence

Greedy policy

\pi \in \mathcal{G}(V) := \argmax_{\pi} \mathcal{T}^\pi V \\ = \argmax_a Q_V(s,a)

One-step improvement

\pi_{t+1} \in \mathcal{G}(V^{\pi_t}) \implies V^{\pi_{t+1}} \ge V^{\pi_t}

Set of greedy policies

Greedy policy choses action that maximizes Q-value

Modified Policy Iteration

Policy improvement    

\pi_{t+1} \leftarrow \argmax_{\pi} \mathcal{T}^\pi V_t
V_{t+1} \leftarrow (\mathcal{T}^{\pi_{t+1}})^m V_t

(Partial) Policy evaluation

\(m = \infty\)  policy iteration

\(m=1\) value iteration

Basic DP algorithm!

Approximate Modified Policy Iteration

Policy improvement    

\pi_{t+1} \leftarrow \argmax_{\pi} \mathcal{T}^\pi \tilde{V}_t
\tilde{V}_{t+1} \leftarrow (\mathcal{T}^{\pi_{t+1}})^m \tilde{V}_t + e_t

Policy evaluation

Errors

RL problem

Optimization ~ mountain descent

RL ~ mountain descent in a bad weather

Safety is critical

Fastest descent might be dangerous due to uncertainty over the landscape...

Safer for learner

For expert

Approximate Modified Policy Iteration

Policy improvement    

\pi_{t+1} \leftarrow \argmax_{\pi} \mathcal{T}^\pi \tilde{V}_t
\tilde{V}_{t+1} \leftarrow (\mathcal{T}^{\pi_{t+1}})^m \tilde{V}_t + e_t

Policy evaluation

Errors

Errors

Estimation errors

finite sample of data

Function approximation errors

neural network value function

Difference between the exact BO and what we compute

Lower bound

The exact BO is uncertain!

Lower bound

Upper bound

\hat{\mathcal{T}}^{\pi_N} V - Cr_N
\hat{\mathcal{T}}^{\pi_N} V + Cr_N
\mathcal{T}^{\pi_N} V

Risk-averse

Exact BO

Overly optimistic

Adversarial Bellman operator

Evaluate with an adversarial policy

\mathcal{T}^{\pi^{\epsilon}} V := \min_{\tilde{\pi} \in \mathcal{U}_{\epsilon}(\pi)} \mathcal{T}^{\tilde{\pi}} V
\mathcal{U}_{\epsilon}(\pi) := \{\tilde{\pi} \in \Delta_{\mathcal{A}}^{\mathcal{S}} \mid D_\text{KL}(\tilde{\pi}(\cdot|s) \| \pi(\cdot|s)) \leq \epsilon(s)\}
\pi
D_{\text{KL}} \leq \epsilon
\pi^{\epsilon}

Convex duality

\mathcal{T}^{\pi^{\epsilon}} V := \min_{\lambda > 0} -\max_{\tilde{\pi}} -\mathcal{T}^{\tilde{\pi}} V - \lambda ( D_{KL}(\tilde{\pi}\|\pi) - \epsilon)

Convex conjugate of \(D_{KL}\)

\langle -Q_V(s,\cdot), \tilde{\pi} \rangle
f^*(y) = \sup_{x \in dom f} \langle x, y \rangle - f(x)

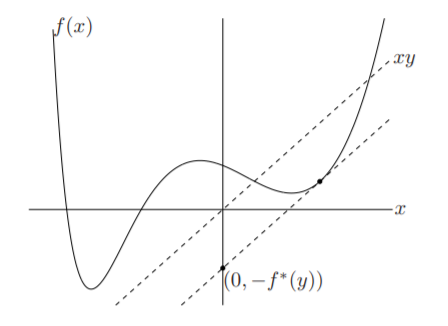
Convex duality

Convex conjugate of \(D_{KL}\) is logsumexp

Maximizing policy is Boltzmann policy

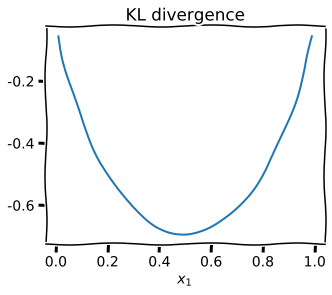
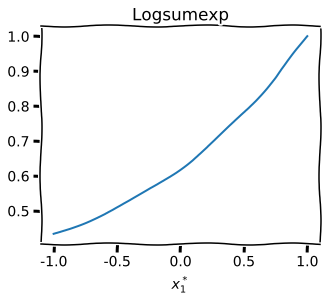
D_{\text{KL}}(p\|p_0):=\mathbb{E}_{x \sim p} \log \frac{p(x)}{p_0(x)}
\log M_{p_0}(u):=\log \mathbb{E}_{x \sim p_0} \exp(u(x))

Adversarial policy

Re-weight policy action probabilities opposite to Q-values

\pi^{\epsilon}(a|s) \propto \exp(-Q_V(s,a)/\lambda_\epsilon(s)) \pi(a|s)
a_1
a_2
a_3
\pi
a_1
a_2
a_3
\pi^\epsilon

adversarial temperature

Optimal adversarial temperature

The right level of conservatism w.r.t. current uncertainty \(\epsilon\)

\lambda^\star(s) := \argmin_{\lambda(s) > 0} \lambda(s) \log \mathbb{E}_{a \sim \pi} \exp(-Q_V(s,a)/\lambda(s)) + \lambda(s) \epsilon(s)

1-D convex optimization (scipy.optimize.bisect)

Too conservative

Too optimistic

\lambda
\lambda^*

Safe Modified Policy Iteration

Policy improvement    

\pi_{t+1} \leftarrow \argmax_{\pi} \mathcal{T}^\pi \tilde{V}_t
\tilde{V}_{t+1} \leftarrow (\mathcal{T}^{\pi^{\epsilon_t}_{t+1}})^m \tilde{V}_t

(Lower bound) Policy evaluation

Slower but safer learning

Convergence

Sub-optimality bound

Define the decrease rate \( \rho = \lim \epsilon_N / \epsilon_{N-1}\).

E_N := \sum_{t=1}^{N-1} \gamma^t \|\epsilon_{N-t}\|_\infty
\|\tilde{V}_N - V^*\|_{\infty} \le \frac{2}{1-\gamma} \left( \frac{R_{\max}}{1-\gamma}E_{N} + \gamma^N \|\tilde{V}_0 - V^*\|_{\infty} \right)

Convergence

  • Slow convergence. If \(\;\rho > \gamma\), then \[ \mathcal \|\tilde{V}_{N}-V^*\|_\infty = \mathcal  O(r_N).\]

Sub-optimality bound

  • (Almost) linear convergence. If \(\;\rho \le \gamma\), then \[\mathcal \|\tilde{V}_{N}-V^*\|_\infty = \begin{cases}\mathcal{O}(\gamma^N), \ \text{if} \ \rho <\gamma,\\ \mathcal{O}(N\gamma^N), \ \text{if} \ \rho = \gamma \end{cases}\]

Convergence

where \(V_t\) is the value function computed via exact evaluation step.

Safety guarantee

\tilde{V}_t \le V_t \le V^*,\; \forall t \in \{1,\ldots,N\}

Adversarial BO and Policy

Safe Modified Policy Iteration

Convergence

Application to continuous control

The normalization constant of the adversarial policy is an intractable integral

Continuous action space

\pi^{\epsilon}(a|s) \propto \exp(-Q_V(s,a)/\lambda_\epsilon(s)) \pi(a|s)

Adversarial BO

[\mathcal{T}^{\pi^\epsilon} V](s) = \lambda(s) \log \mathbb{E}_{a \sim \pi} \exp(Q_V(s, a)/\lambda(s))

Risk-neutral \(\lambda \rightarrow \infty\)

Risk-seeking \(\lambda > 0\)

Risk-averse \(\lambda < 0\)

\lambda < 0

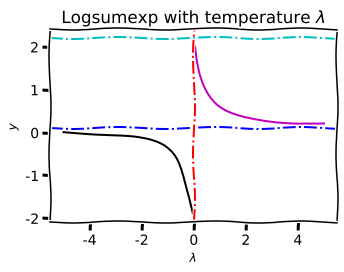
log-moment generating function

[\mathcal{T}^{\pi^\epsilon} V](s) \simeq [\mathcal{T}^\pi V](s) - \frac{\text{Var}_\pi(Q_V(s,\cdot))}{2\lambda}
\lambda^\star(s) \simeq \sqrt{\frac{\text{Var}_\pi(Q_V(s, \cdot))}{2\epsilon}}

Approximate Adversarial BO

Taylor series of logsumexp up to the 2nd order at \(\lambda \rightarrow \infty\)

\langle Q_V(s,\cdot), \pi \rangle

ABO ~ BO + variance penalization

Safe reward shaping

ABO ~ BO + variance penality = reward change

\tilde{r}(s,a,s') := r(s,a) + \\ \frac{1}{2\lambda}(\gamma \text{Var}_{\tilde{a} \sim \pi}(Q(s', \tilde{a})) - \text{Var}_{\tilde{a} \sim \pi}(Q(s, \tilde{a})))

For \(\lambda > 0\) encourages to visit states with smaller variance

One-line change to implement safety!

Gaussian policies

Variance for safe reward shaping

Using Taylor expansion of Q-values around mean action

\text{Var}_{a \sim \pi}(Q(s,a)) \simeq g_0(s)^T \Sigma(s) g_0(s)
\pi(a|s) = \mathcal{N}(\mu(s), \Sigma(s))
g_0(s) := \nabla_a Q(s,a)|_{a=\mu(s)}

Approximate BO

Safe reward shaping

Variance of Q-values

 

SOTA: regularized RL

\pi^* = \argmax_\pi(V^\pi - \alpha H(\pi))

Regularized Bellman operator

\mathcal{T}^\pi_\Omega := \mathcal{T}^\pi V - \alpha H(\pi)

Entropy regularizer

H(\pi(\cdot|s)) := \mathbb{E}_{a \sim \pi} \log \pi(a|s)

Safe Soft Actor-Critic

Soft Actor-Critic + Safe Reward Shaping

Cautious short-term and optimistic long-term!

Entropy-regularized SOTA

Simple reward modification

Hopper

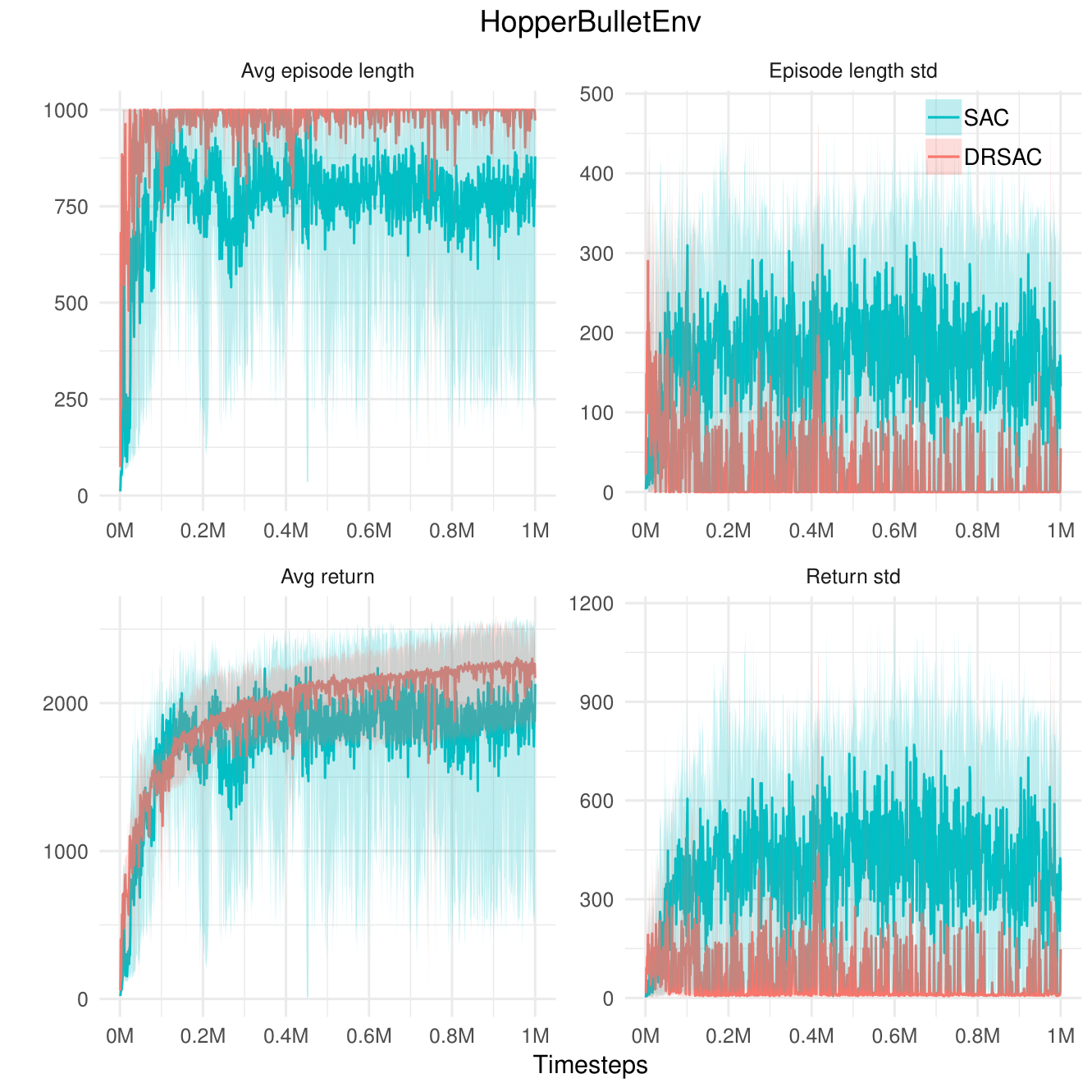
Longer episodes

Stable learning score

SAC (Baseline) vs. Safe SAC (Proposed)

Walker2D

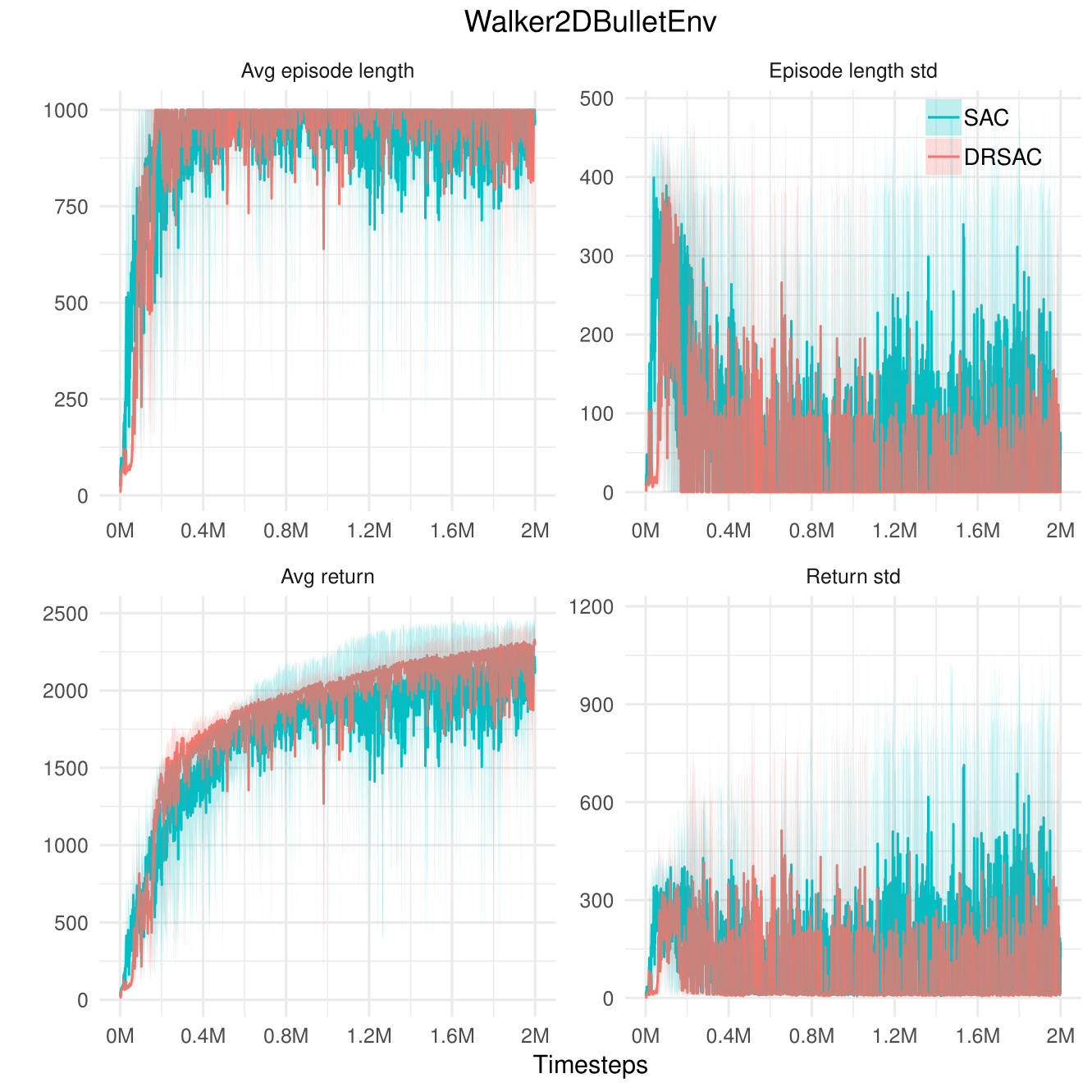
Quite stable already

Stable learning score

SAC (Baseline) vs. Safe SAC (Proposed)

Test performance of Safe SAC

Hopper Walker2D
Return Avg Similar Similar
Return Std -76% +/- 21 -78% +/- 48
Episode Len Avg Similar Similar
Episode Len Std -76% +/- 13 -77% +/- 42

Percent change w.r.t. SAC

Hopper

Walker2D

Code available!

https://github.com/bandofstraycats/dr-sac

Using PyBullet simulator environment

def _get_adv_reward_cor(self, q1_mu, q1_mu_targ, mu, mu_targ, std, std_targ):
	# state visit counter
	n_s = self._n_s_ph if self._use_n_s else self._total_timestep_ph
	# size of uncertainty set
	adv_eps = tf.divide(self._adv_c, tf.pow(tf.cast(n_s, tf.float32), self._adv_eta))

	# approximate standard deviation of Q-values at current and next states
	g0 = tf.gradients(q1_mu, mu)[0]
	g0_targ = tf.gradients(q1_mu_targ, mu_targ)[0]
	approx_q_std = self._approx_q_std_2_order(g0, q1_mu, mu, std, self._observations_ph)
	approx_q_std_targ = self._approx_q_std_2_order(g0_targ, q1_mu_targ, mu_targ, std_targ, 
    					self._next_observations_ph)
	
	# approximate adversarial parameter
	adv_lambda = tf.divide(approx_q_std, tf.sqrt(2*adv_eps))
	
	# safe reward correction (simplified by substituting lambda approximation)
	adv_reward_cor = 1. / (2*adv_lambda) * 
    					(self._discount*approx_q_std_targ - approx_q_std)
	return adv_reward_cor

Summary

lower bound w.r.t. estimation errors

using convex duality

to the optimal policy

approximation for continuous control

exploration strategy

Safety

Scalability

Convergence

Safe reward shaping

Short-term risk-averse and long-term risk-seeking

References

  1. T. Haarnoja, A. Zhou, P. Abbeel, and S. Levine. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. arXiv preprint arXiv:1801.01290, 2018.
  2. B. Scherrer, M. Ghavamzadeh, V. Gabillon, B. Lesner, and M. Geist. Approximate modified policy iteration and its application to the game of tetris. Journal of Machine Learning Research, 16:1629–1676, 2015
  3. E. Smirnova, E. Dohmatob, J. Mary. Distributionally robust reinforcement learning. RL4RealLife workshop, ICML 2019. arXiv preprint arXiv:1902.08708, 2019

Take home message

Safety is related to variance

Right level of pessimism is healthy!

Scalability through separability

Think big, take small steps!