Basisconcepten

2 (of meer) verzamelingen \(A, B\) geven ons de kans om interessante, nieuwe objecten te definiëren
Cartesisch product \(C = A \times B \)
bestaat uit alle mogelijke tupels \(t = (a,b)\) met \(a \in A, b \in B\)
Relatie \(R \subseteq C\)
bestaat uit tupels \(t = (a,b)\) met \(a \in A, b \in B\),
drukt bijgevolg een verband uit tussen elementen uit \(A\) en \(B\)
Relaties zijn dermate interessant dat specifieke types een eigen naam krijgen:
- Functies
- Afbeeldingen
- Injecties
- Surjecties
- Bijecties

Basisconcepten

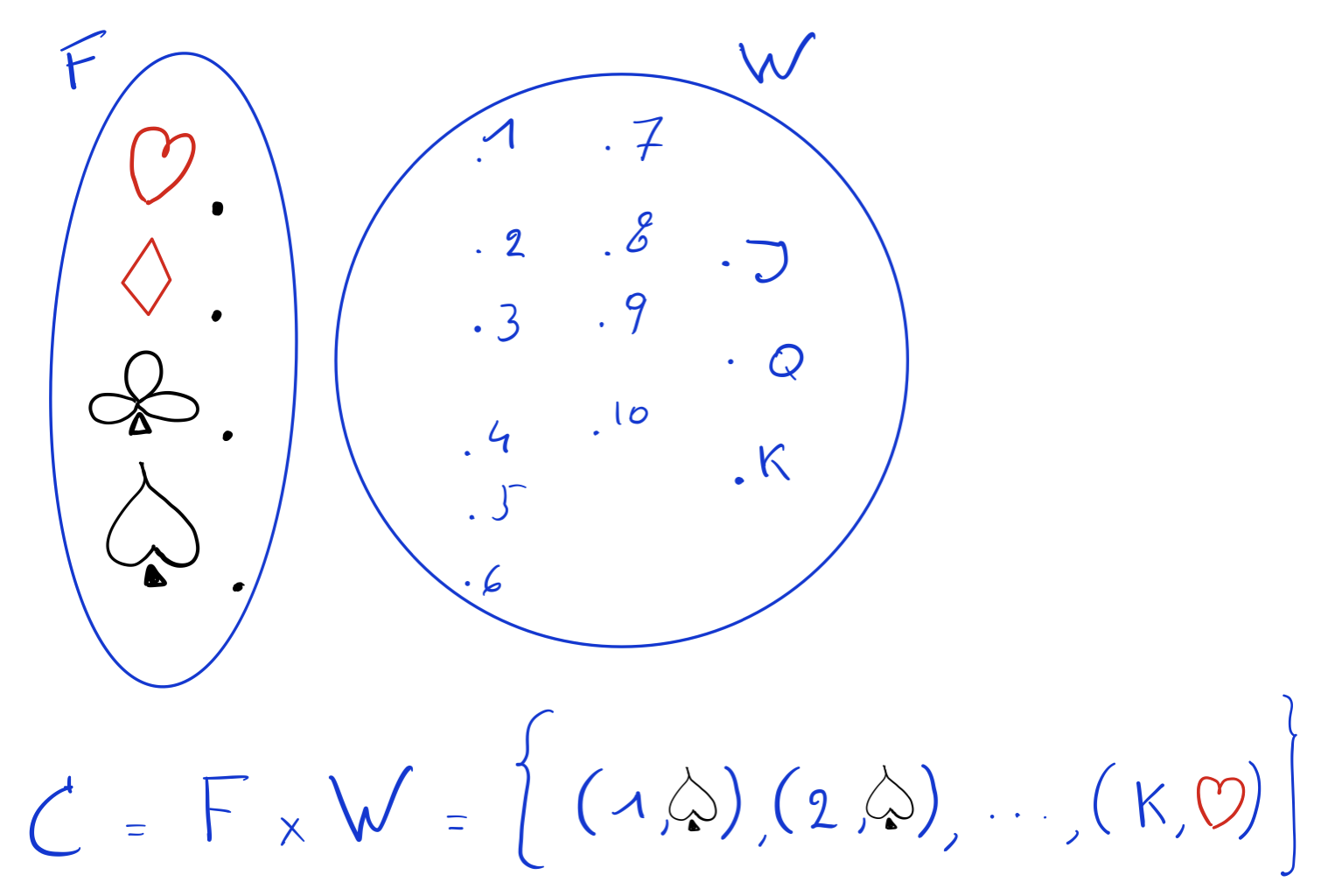
Voorbeeld cartesisch product: boek speelkaarten

W \times F

Basisconcepten

Voorbeeld relatie als deelverzameling cartesisch product

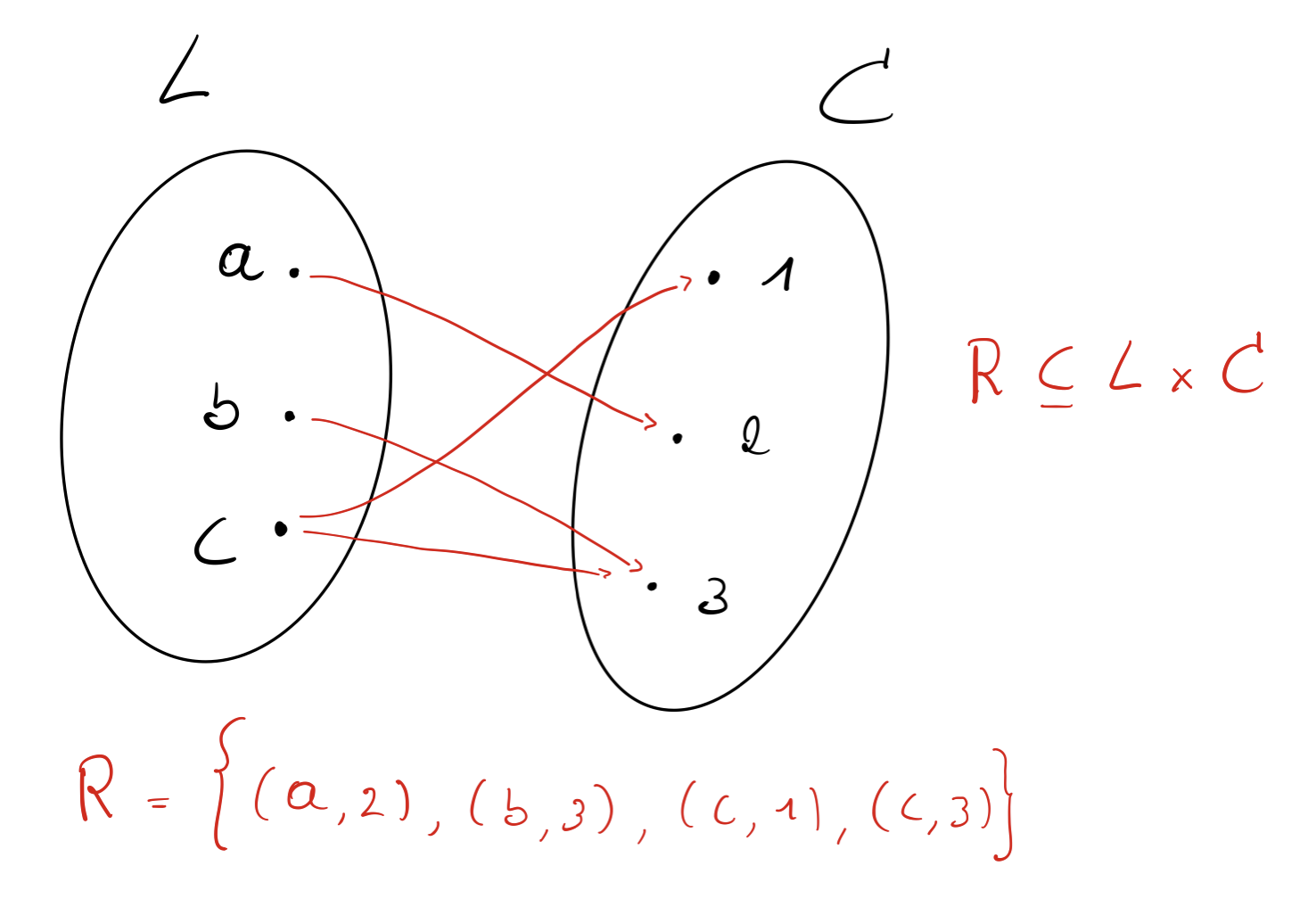
Basisconcepten

Soorten relaties

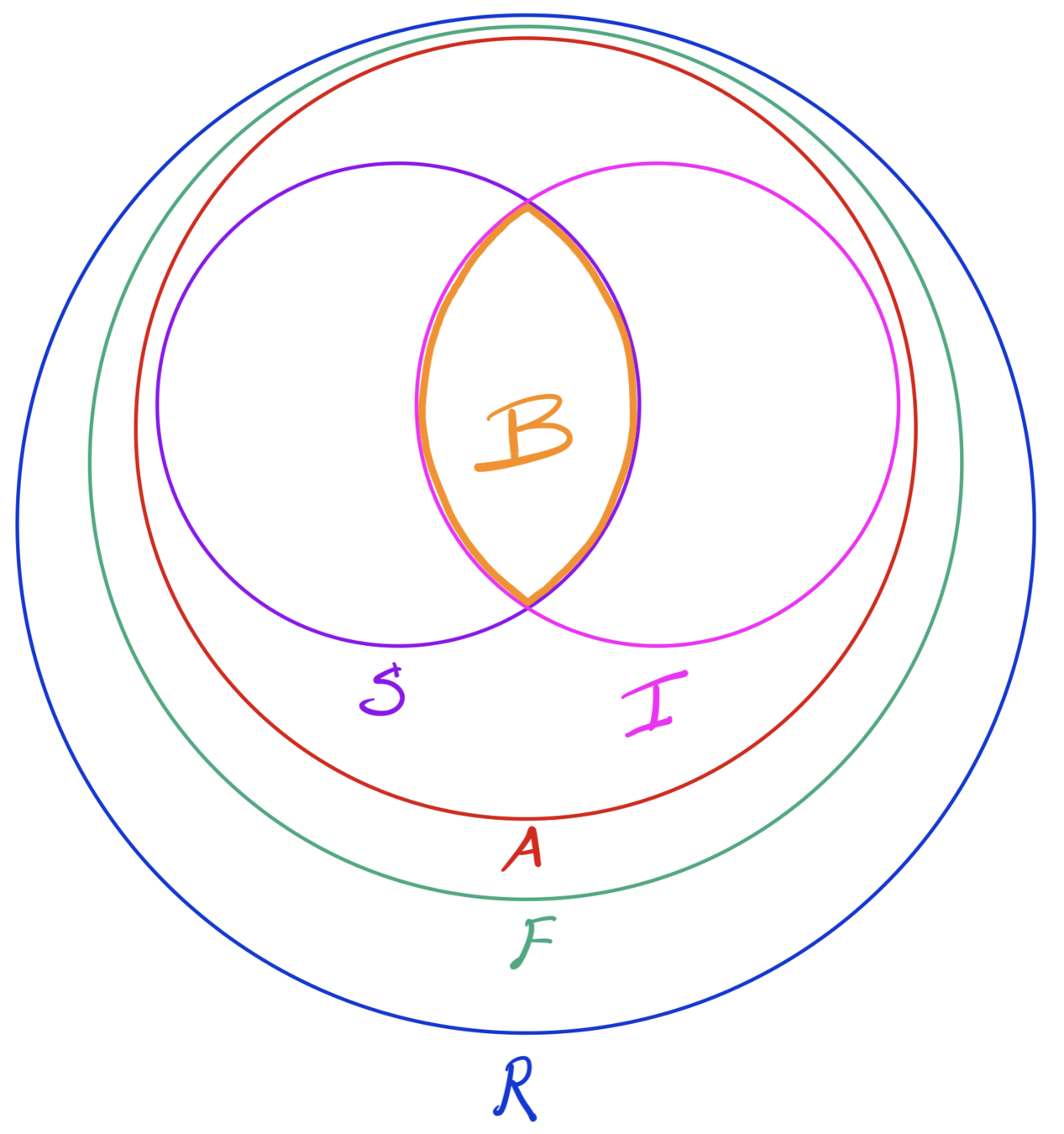
- Bijecties

- Surjecties

- Injecties

- Afbeeldingen

- Functies

- Relaties

Soorten relaties

- Bijecties

- Surjecties

- Injecties

- Afbeeldingen

- Functies

- Relaties

Oefeningen

Oefening 5.3

Beschouw de volgende relaties:

Volgt: geeft aan welke studenten welke vakken volgen
ECTS: geeft aan hoeveel ECTS-punten elk vak waard is
Score: geeft aan welke student, op welk vak, welke score behaald heeft
Geslaagd: geeft aan welke studenten voor welke vakken geslaagd zijn

Gevraagd:

Welke cartesische producten?
Schrijf in symbolen: een student heeft enkel een score voor de vakken die hij/zij volgt
Een student slaagt bij een score van minstens 10. Definieer een nieuwe relatie Geslaagd, obv van de voorgaande.

Oefening 5.3

Gevraagd:

Welke cartesische producten?
Schrijf in symbolen: een student heeft enkel een score voor de vakken die hij/zij volgt
Een student slaagt bij een score van minstens 10. Definieer een nieuwe relatie Geslaagd, obv van de voorgaande.

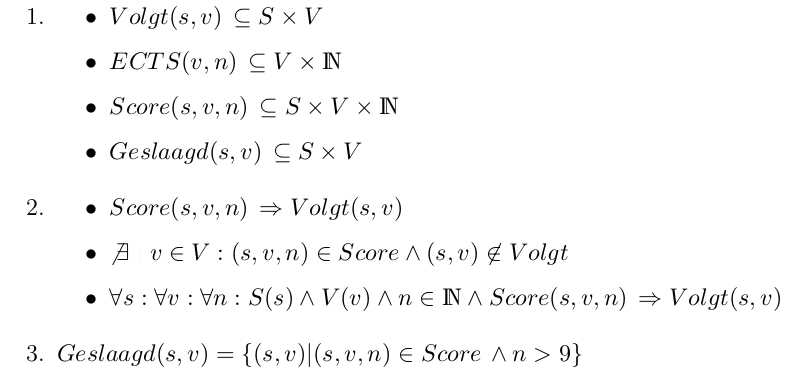
Volgt: geeft aan welke studenten welke vakken volgen
ECTS: geeft aan hoeveel ECTS-punten elk vak waard is
Score: geeft aan welke student, op welk vak, welke score behaald heeft
Geslaagd: geeft aan welke studenten voor welke vakken geslaagd zijn

Oefening 5.5 - 5.6

Zij \(M\) de verzameling van alle mensen, en \(R \subseteq M\) een relatie

5.5: Stel \(R\) is de relatie "... is een ouder van...", wat is haar inverse \(R^{-1}\) ?
\(R^{-1}\) is "...is een kind van...." of "...heeft als ouder..."
5.6: Stel \(R\) is de relatie "...heeft als ouder...", wat is de samengestelde \(R \circ R\)?
\(R \circ R\) is dan "...heeft als grootouder..."

Oefening 5.9

Opgave: Geldt in het algemeen dat \(R \circ S = S \circ R\)?

Oefening 6.1

Opgave: Is \(R\) een functie, of \(R^{-1}\), of geen van beiden?

De relatie \(R\) is een functie als \(R \in \{R_1, R_4, R_6, R_7\}\)
De relatie \(R^{-1}\) is een functie als \(R \in \{R_4, R_5, R_7\}\)

Oefening 6.4

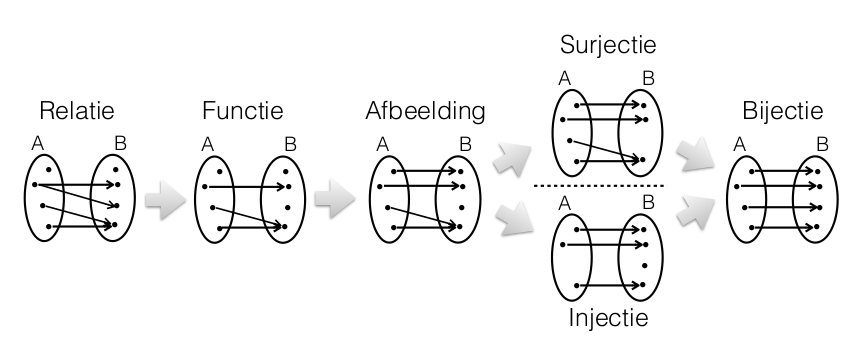
Opgave: Duid in figuur 6.1 op het diagram bij “relatie” aan welk element
van A of B ervoor zorgt dat de relatie geen functie is. Duid bij het diagram bij “functie” aan welk element ervoor zorgt dat de functie geen afbeelding is, en zoverder voor afbeelding, surjectie en injectie.

Oefening 6.13

Opgave: Bewijs dat de identiteitsfunctie een bijectie is.

Herschrijf (40): \(f(x) \not = f(x') \Rightarrow x \not = x'\)

Bewijs uit het ongerijmde:
- stel \(x = x'\)
- \(\Leftrightarrow i(x) = i(x') \)
- \(\Leftrightarrow f(x) = f(x') \)

Die laatste regel is strijdig met \(f(x) \not = f(x') \) dus \(x = x'\) kan nooit.