MERCS

Multi-directional Ensembles of

Regression and Classification Trees

Outline

  1. Introduction
  2. MERCS
  3. Anomaly Detection
  4. Outlook

Outline

  1. Introduction
  2. MERCS
  3. Anomaly Detection
  4. Outlook

Introduction

What is the relationship of

Machine Learning to other sciences?

Standard problem of ML

f: X \rightarrow Y
f:X→Yf: X \rightarrow Y

Given:

Derive:

D = \{x^1, \cdots, x^n \}
D={x1,⋯,xn}D = \{x^1, \cdots, x^n \}
x^i = \{x_1, \cdots, x_m \}
xi={x1,⋯,xm}x^i = \{x_1, \cdots, x_m \}
A = \{A_1, \cdots, A_m \}
A={A1,⋯,Am}A = \{A_1, \cdots, A_m \}
\forall i,j: x^i_j \in Dom(A_j)
∀i,j:xji∈Dom(Aj)\forall i,j: x^i_j \in Dom(A_j)
X, Y \subset A
X,Y⊂AX, Y \subset A
X \cap Y = \emptyset
X∩Y=∅X \cap Y = \emptyset

Standard problem of ML

D
DD
f
ff
X
XX
\rightarrow
→\rightarrow
Y
YY

N.b.:

Some of the red entries have to be known in order to achieve this!

Different flavours of ML

f: X \rightarrow Y
f:X→Yf: X \rightarrow Y

This encompasses many kinds of ML

  • Function approximation
    (cf. optimization)
  • Probabilistic learning
  • Explicit modeling

Correspond to various kinds of f

Different flavours of ML

f: X \rightarrow Y
f:X→Yf: X \rightarrow Y

This encompasses many kinds of ML

  • Predictive models
  • Generative models

Correspond to various X, Y

Different flavours of ML

f: X \rightarrow Y
f:X→Yf: X \rightarrow Y

This encompasses many kinds of ML

  • Supervised learning
  • Semi-supervised learning
  • Unsupervised learning

Correspond to

feedback available to the algorithm

while learning f

How does this relate to the rest?

Machine Learning is just another kind of mathematical tool, that can be used to address questions in science and engineering

We start from data and rely on algorithms, rather than searching for a reasonable f ourselves.

4 ways of doing science

  1. By developing theories
  2. By performing experiments
  3. By performing simulations
  4. By looking at the data

Where does anomaly detection fit in?

Nowhere?

Anomaly detection is hard,

precisely because

f is not easily defined

Where does anomaly detection fit in?

Many approaches exist,

2 key ideas:

  1. Learn a model of the normal data (~generative approach), flag things that do not correspond to this as anomalies
     
  2. Convert to the canonical form,
    learn to
    detect known anomalies explicitly

Outline

  1. Introduction
  2. MERCS
  3. Anomaly Detection
  4. Outlook

MERCS

Motivation

``Flexibility matters.

Any truly intelligent system must not only possess the ability to solve a task, but must also exhibit considerable flexibility with regard to the task itself.''

Research Goal

f: X \rightarrow Y
f:X→Yf: X \rightarrow Y

But, now:

  • \(X\) is not given at training time
  • \(Y\) is not given at training time

This is what we call a versatile model

Motivation

Can we lift an ensemble of predictive models to reveal the general structure of a given dataset?

Motivation

Discovering general structure is typically the domain of probabilistic methods,

i.e. Bayesian Networks.

Bayesian Network

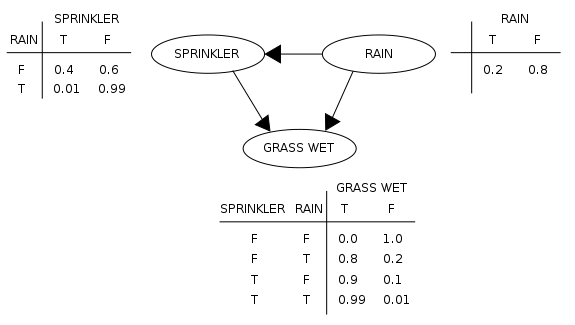
Motivation

Can it be done differently?

 

Can it be done by methods that are more suitable for big data?

The model

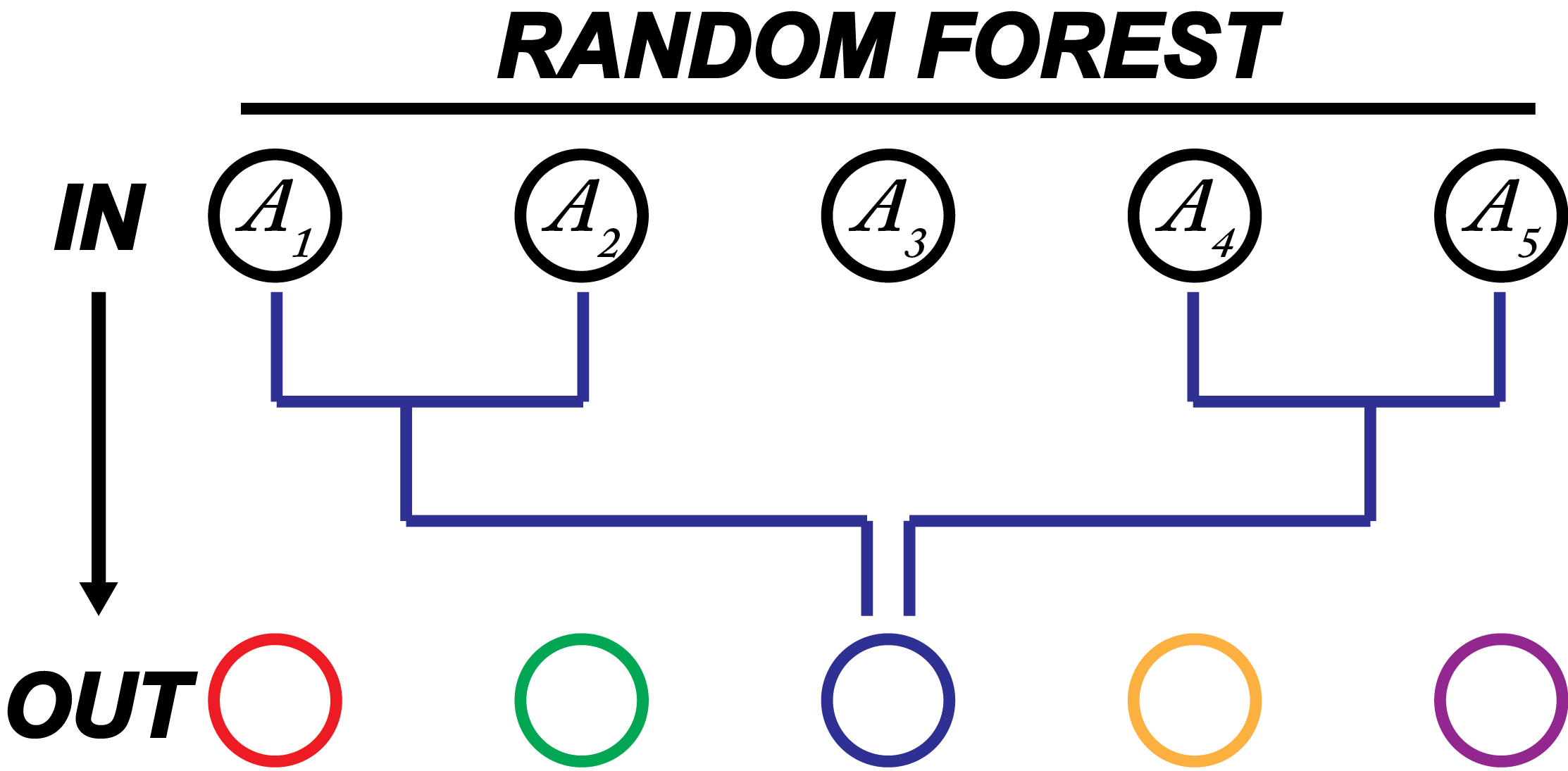
The model

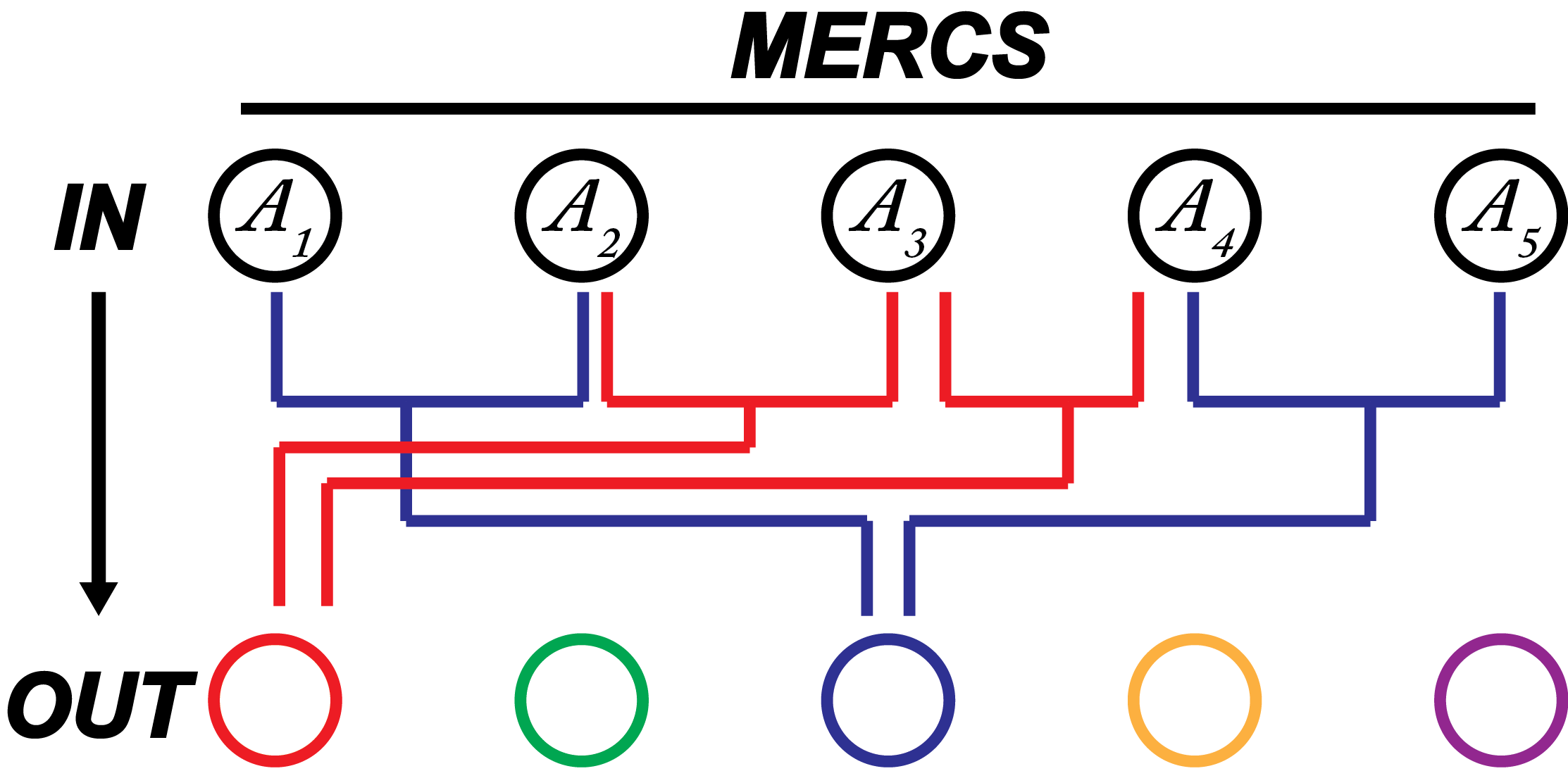
Some properties

+

-

  • Interpretable
  • Scalable
  • Numeric and nominal attributes
  • Exponential: Including every possible f  (~tree) is impossible
  • Predictive: Decision trees do not offer actual probabilistic reasoning (\(\leftrightarrow\) Bayesian Networks)

Main challenge

Including every possible f  is infeasible

1. We include a sample of possible trees in our ensemble
 

2. When presented with a prediction task,

we combine those trees appropriately

1. Make a selection of lego blocks

 

2. Build what you need with those lego blocks

Predictions in MERCS

There are 2 ways of building:

  1. Build ensembles of trees
  2. Build chains of trees

Example:

MAFI prediction strategy

Select most appropriate trees, based on feature importance

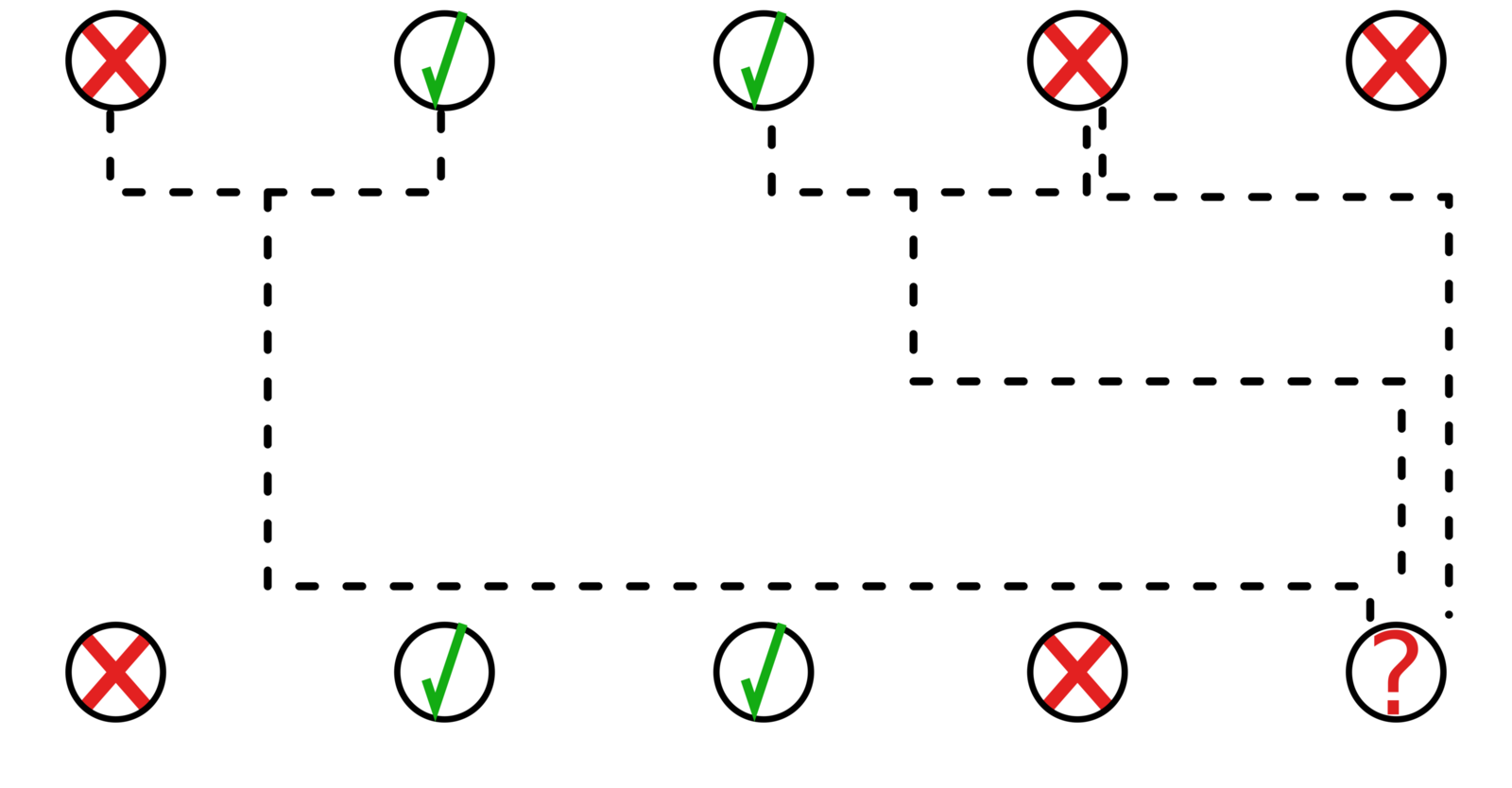
Example:

MAFI prediction strategy

Select most appropriate trees, based on feature importance

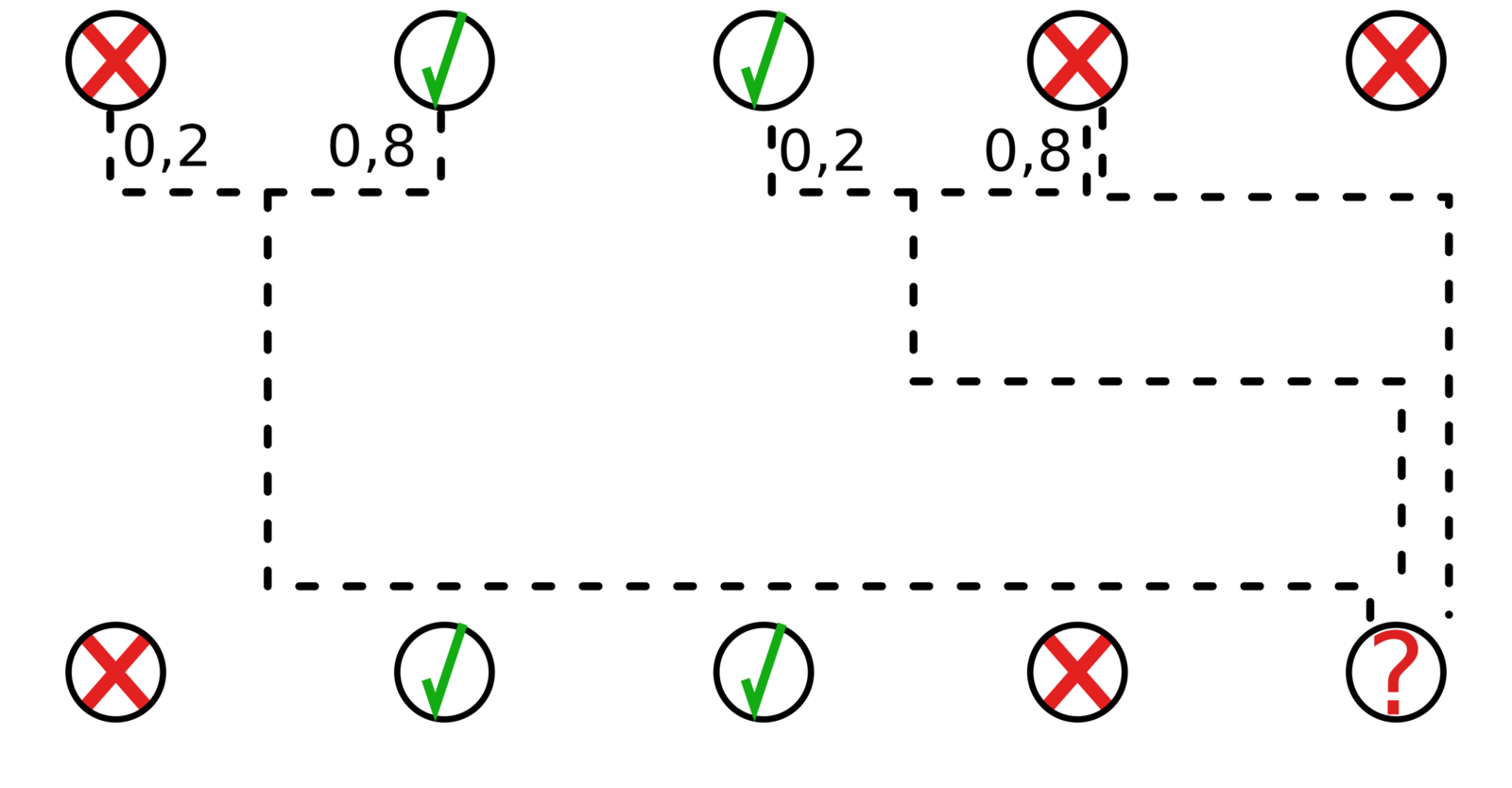
Example:

MAFI prediction strategy

Select most appropriate trees, based on feature importance

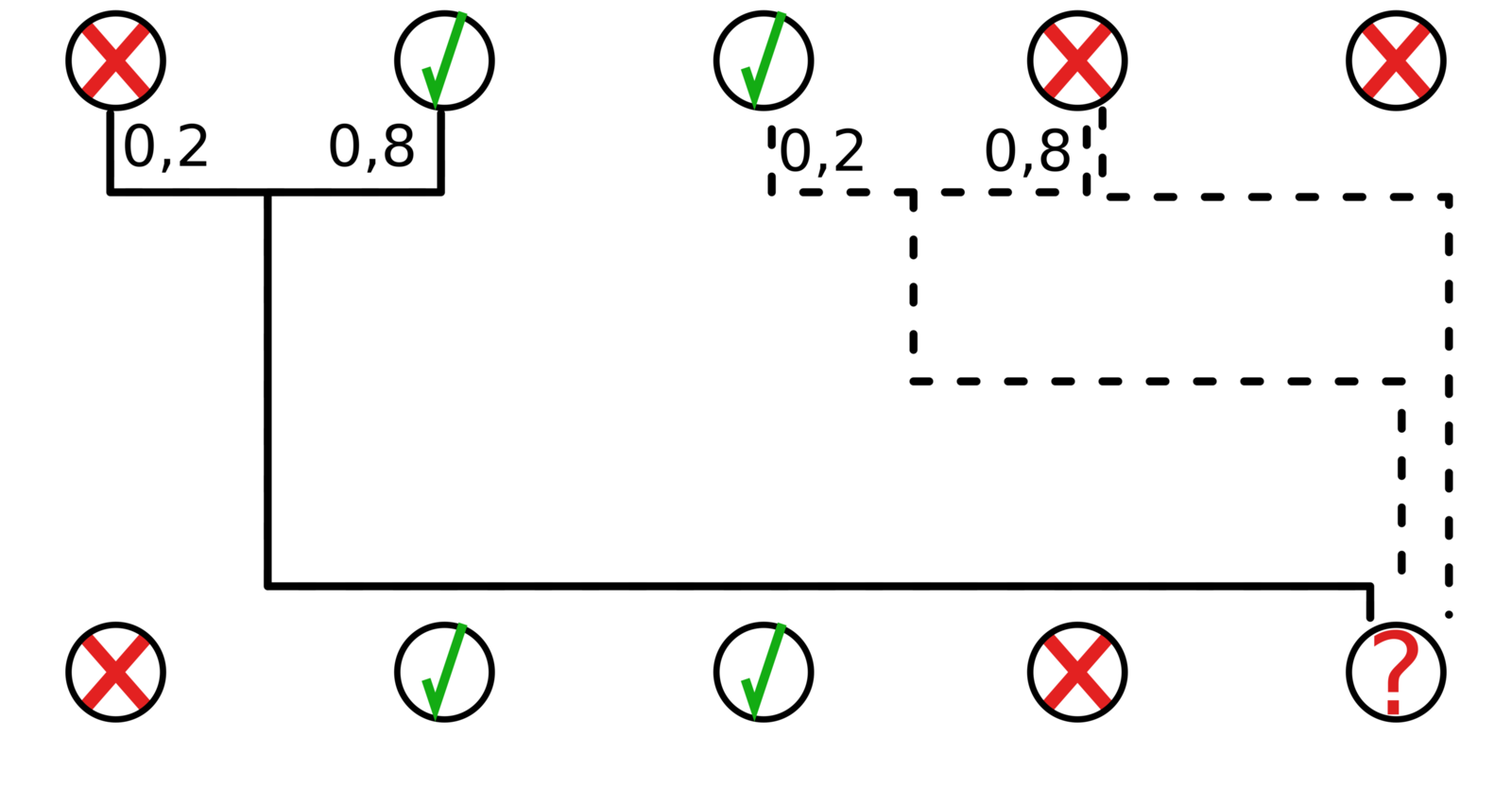
Example:

RW prediction strategy

Do Random Walks in the MERCS model

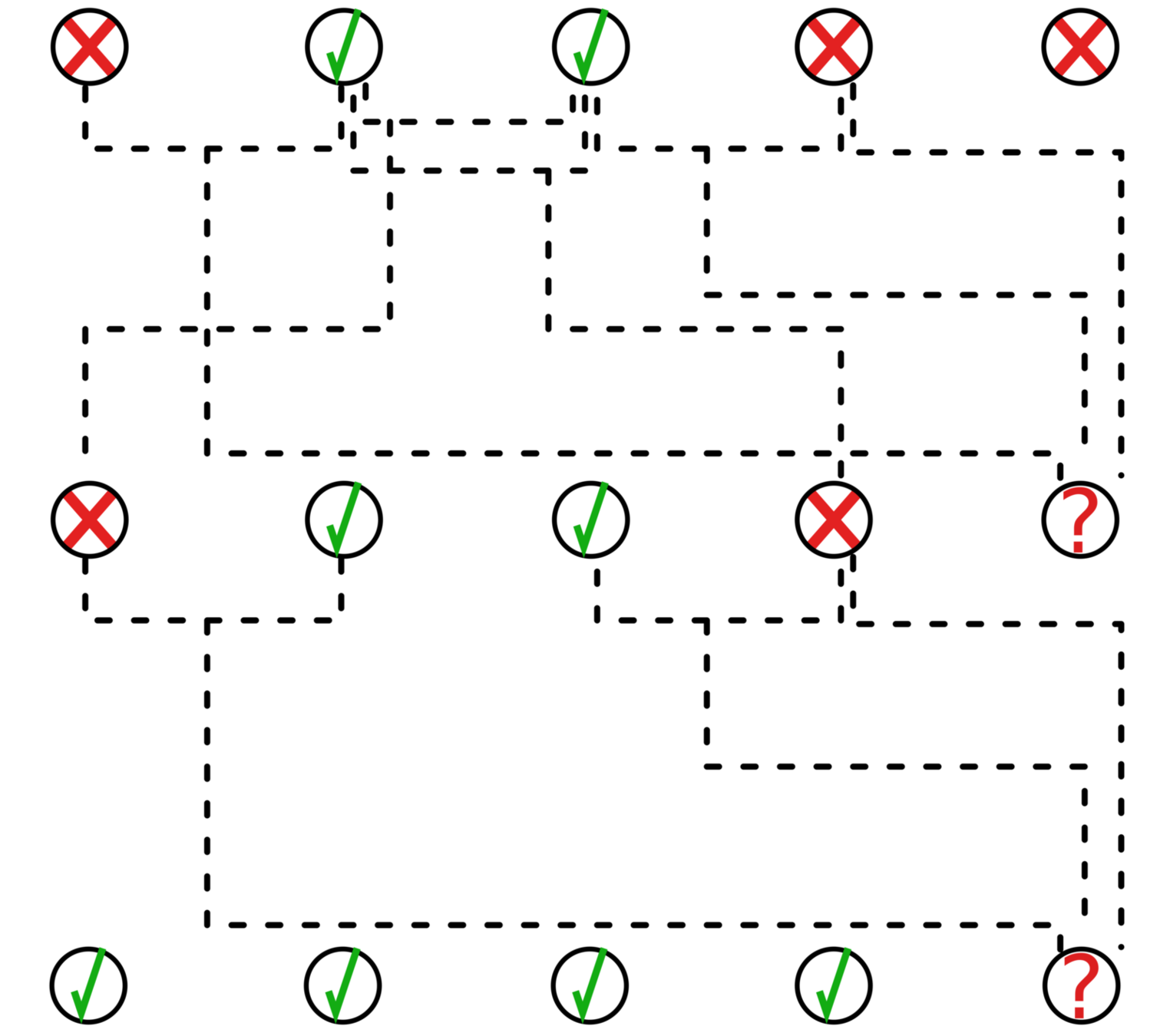
Example:

RW prediction strategy

Do Random Walks in the MERCS model

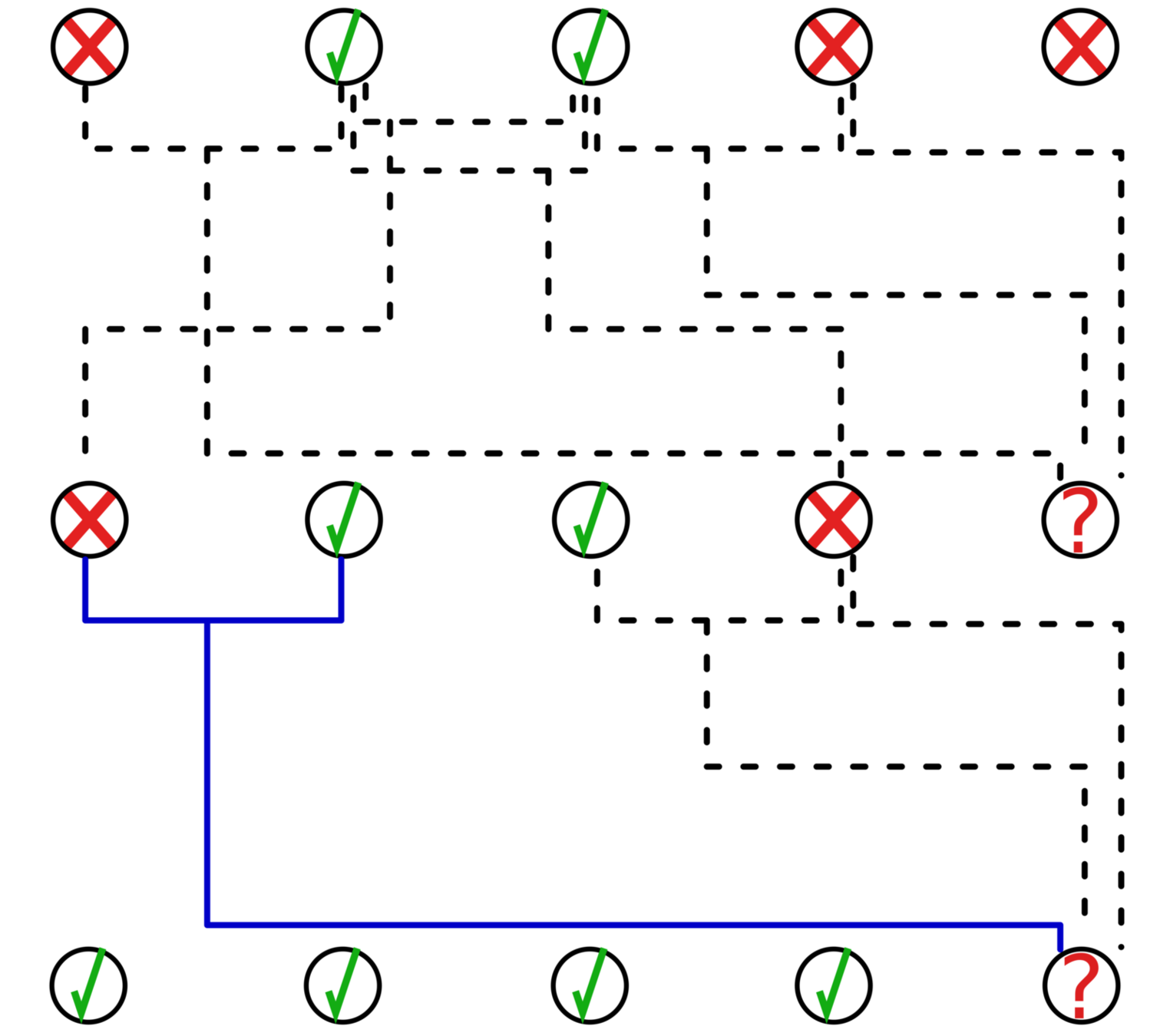
Example:

RW prediction strategy

Do Random Walks in the MERCS model

Example:

RW prediction strategy

Do Random Walks in the MERCS model

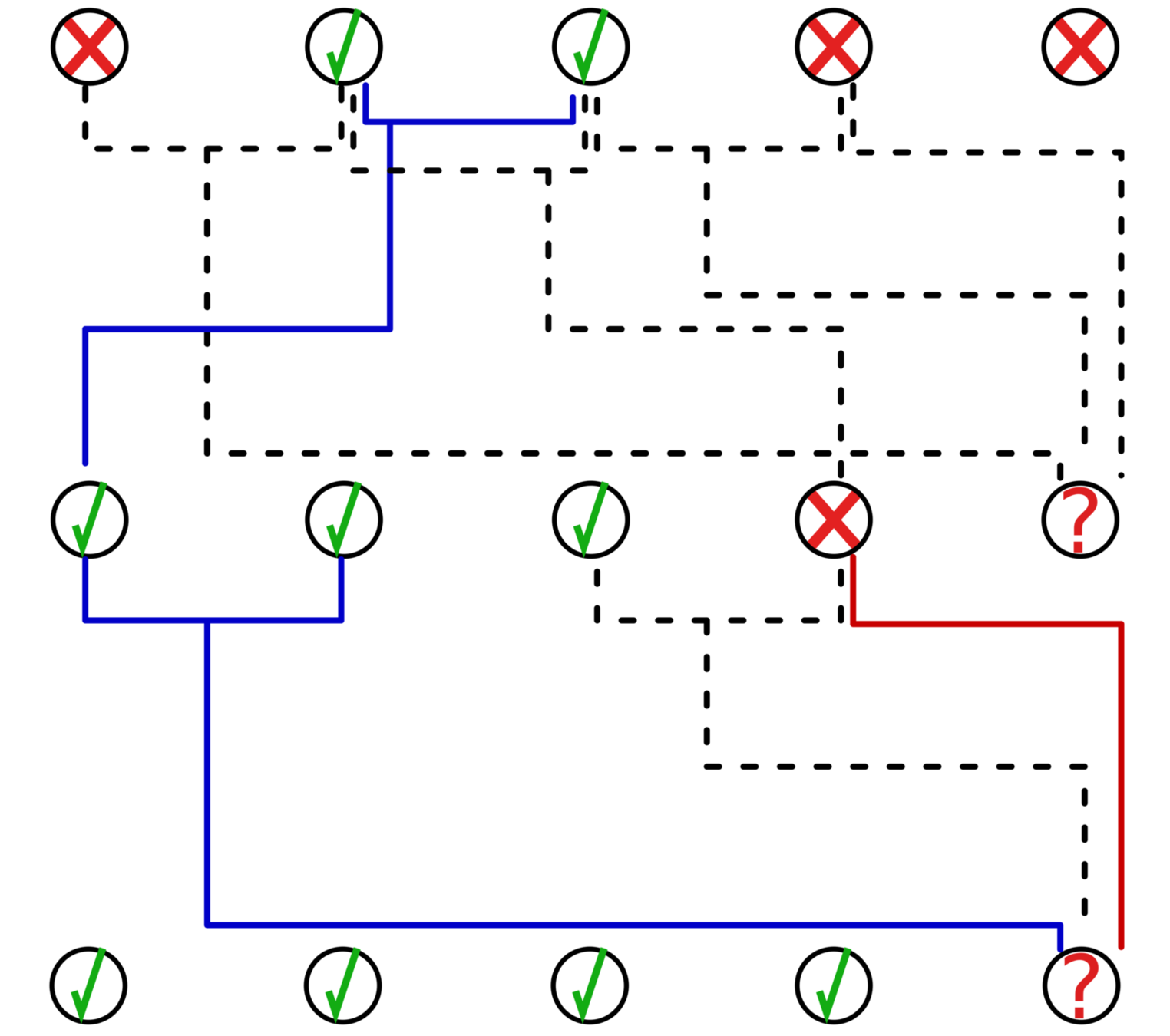
Example:

RW prediction strategy

Do Random Walks in the MERCS model

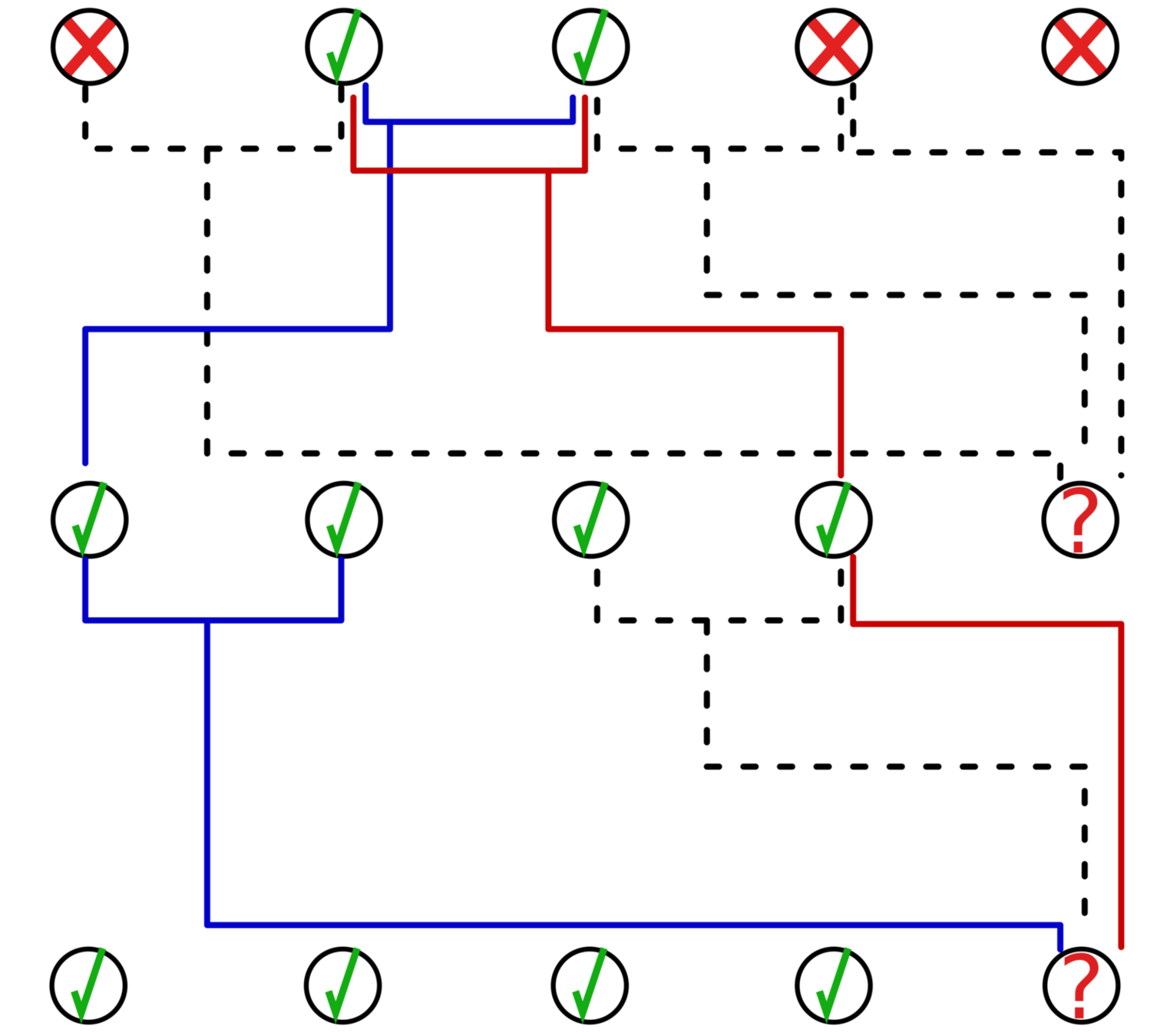
Conclusions

on prediction strategies

  • Appropriateness is a very important criterion to compose an ensemble
  • Chaining is pretty powerful to introduce more flexibility
  • Time - Performance tradeoff

Application areas (1)

Machine Learning in spreadsheets

The task is to predict entries in a particular column from data present in the rest of the spreadsheet.

Missing data (i.e., empty cells) requires some degree of flexibility on the prediction algorithm to cope with changes in the available information (i.e., changing \(X\))

Application areas (2)

Anomaly detection for industrial applications.

Ideally, an algorithm designed to detect anomalies in this context needs to exhibit some degree of robustness against this kind of small, but common malfunctions.

Here, complex machines are monitored by many sensors and not every data source may function properly all the time.

Outline

  1. Introduction
  2. MERCS
  3. Anomaly Detection
  4. Outlook

MERCS

for

Anomaly Detection

MERCS for anomaly detection

  1. Residual analysis
  2. Clustering approach

MERCS for anomaly detection

Residual analysis

Using the flexible predictions that MERCS allows to detect anomalies:

  1. Predict every attribute from all the other available ones
  2. Verify whether observations deviate from predictions
  3. If the deviation (i.e. the residual) exceeds a certain threshold, flag as anomaly

MERCS for anomaly detection

Residual analysis

When we cannot predict something correctly,

this indicates an anomaly

MERCS for anomaly detection

Clustering analysis

A decision tree implicitly defines a hierarchical clustering

  1. Every node in a decision tree
    splits the parent node
  2. Those two new parts can be regarded as two new clusters of data points
  3. If an observed value is very atypical in its clusters, flag as anomaly

MERCS for anomaly detection

Clustering analysis

Use the structure as represented by the several clusters to detect anomalies

Outline

  1. Introduction
  2. MERCS
  3. Anomaly Detection
  4. Outlook

Outlook

Low-hanging fruit

  • Root cause analysis
  • Try more off-the-shelf algorithms
  • Smarter feature selection
  • Why was one year
    so much easier than the other?

Interesting possibilities

  • See if MERCS can mean something
  • More attention to temporal component
  • Semi-supervised approaches (user-feedback)

Questions

+

 Discussion