Dual Quaternions Demystified

DUAL QUATERNIONS DEMYSTIFIED

Today :

Why dual quaternions
Half of the PGA picture
Formalizing Geometry
The Space Hack
Symmetry Groups
Geometry as invariants
The Sandwich Hack
Exercises
Brutally violating PGA
The Conformal Group

DUAL QUATERNIONS DEMYSTIFIED

Popular in Computer Graphics for solving the 'candy wrapping' artefact.

\text{v}_{\text{out}} = \sum\limits_{i=0}^{n}w_{i}A_{i}\text{v}_{\text{in}}

\text{Q} = \sum\limits_{i=0}^{n}w_{i}\text{Q}_{i}\\ \text{v}_{\text{out}} = e^{\text{Q}}\text{v}_{\text{in}}e^{\text{-Q}}

Can't blend matrices

Can blend dual quaternions

DUAL QUATERNIONS DEMYSTIFIED

Popular in Mechanics, Robotics, for unifying translation and rotation.

\begin{pmatrix}F\\\tau\end{pmatrix} = \begin{pmatrix}m \mathbf I_3 & 0\\ 0 & \mathbf I_{\text{cm}} \end{pmatrix} \begin{pmatrix}\mathbf a_{\text{cm}} \\ \alpha \end{pmatrix} +\begin{pmatrix}0 \\ \omega \times \mathbf i_{\text{cm}}\omega \end{pmatrix}

{\dot{\mathbf v}}_b = 2\mathbf A^{-1}(\mathbf F_b+(\mathbf m_b \times \mathbf v_b))

3x3 Matrices

vectors

Dual Quaternions

Treat translation/rotation separately

One formula for both rotations and translations

translation

rotation

DUAL QUATERNIONS DEMYSTIFIED

Typically introduced algebraically, using one of many options ..

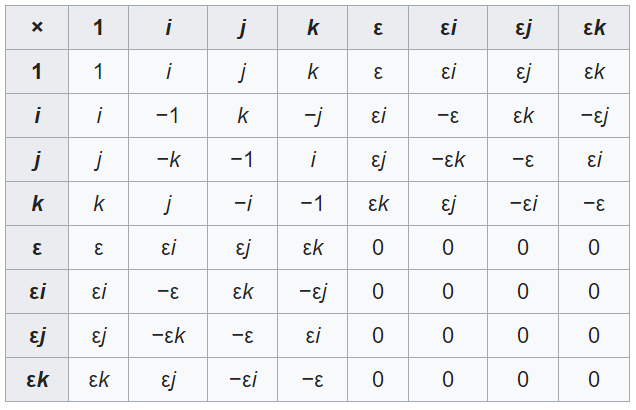
Multiplication Table

Tensor Product

\(\mathbb H \otimes \mathbb D\)

Quaternions

Dual Numbers

.. not very insightful or intuitive ..

explanations talk about 4D spheres .. that is just cruel.

DUAL QUATERNIONS DEMYSTIFIED

Why are they so hard to understand?

They are only half of the picture. The dual quaternions

are the even subalgebra of a geometric algebra called PGA.

\(\mathbb R_{3,0,1}\)

DUAL QUATERNIONS DEMYSTIFIED

Same as opening but now in PGA - implementation is shorter than function names !

no coordinates - no chirality - no gimbal lock - no conversions

point

direction

position

rotation

matrix

quaternion

// construct transformations -> motors, not matrices !
translate (x,y,z)             = E**(x*e01+y*e02+z*e03)
rotate_euler (h,p,b)          = E**(b*e12)*E**(p*e23)*E**(h*e13)
rotate_axis_angle (x,y,z,a)   = E**(a*x*e23+a*y*e13+a*z*e12)
look_at (from,too,pole)       = (1 + (e1-from)*(to-from))

// apply transformations -> note : all the same..
transform_point (M, p)        = M*p*~M
transform_direction (M, d)    = M*d*~M
transform_line (M, l)         = M*l*~M
transform_plane (M, P)        = M*P*~M

line

plane

// construct lines
line_from_points (p1, p2)           = p1&p2 
line_from_points_and_dir (p, d)     = p&(p+d)


// construct planes
plane_from_points (p1,p2,p3)        = p1&p2&p3
plane_from_point_and_dirs (p,d1,d2) = p&(p+d1)&(p+d2)
plane_from_points_and_dir (p1,p2,d) = p1&p2&(p1+d)
plane_from_point_and_line (p,l)     = p&l 
plane_from_equation (a,b,c,d)       = ae1+be2+ce3-de0

// construct transformations
quat_from_euler (h, p, b)
quat_from_axis_angle (x, y, z, a)
quat_look_at (from, too, pole)
quat_from_matrix (M)
quat_to_matrix (Q)

// apply transformations
transform_point (Q, p)
transform_line (Q, l)
transform_plane (Q, P)

// Intersections
intersect_line_plane (l, P)       = l^P
intersect_plane_plane (P1, P2)    = P1^P2
intersect_planes (P1, P2, P3)     = P1^P2^P3

// Projections
project_point_plane (p, P)        = P|p*P
project_line_plane (l, P)         = P|l*P
project_point_line (p, l)         = l|p*l

DUAL QUATERNIONS DEMYSTIFIED

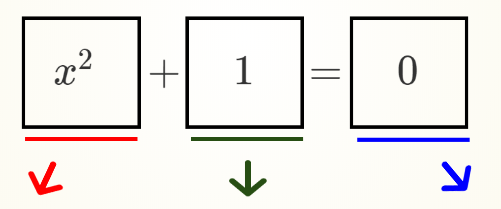
\({\mathbf e_-}^2=-1\)

\({\mathbf e_+}^2=1\)

\({\mathbf e_0}^2=0\)

Introduce Geometric Numbers
Use them to define Geometric Primitives (points, lines, planes)
Figure out how these primitives Transform

CONTROVERSIAL: vectors are Planes, trivectors are Points

we understand the controversy, it is caused by how we are used to formalize geometry ...

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

DUAL QUATERNIONS DEMYSTIFIED

Euclid's first attempts at preserving his ideas and formalising geometry had difficultties.

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R^3\)

Euclid's first attempts at preserving his ideas and formalising geometry had difficultties.

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R^3\)

vectors \(\mathbb R^3\)

Points

Directions

Lines

Planes

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R^3\)

vectors \(\mathbb R^3\)

matrices \(\mathbb R^{3\times3}\)

Points

Directions

Translations

Rotations

Lines

Planes

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R^3\)

vectors \(\mathbb R^3\)

matrices \(\mathbb R^{3\times3}\)

Points

Directions

Translations

Rotations

\([M_{ab},V_{ab}] = [M_aM_b,M_aV_b+V_a]\)

Lines

Planes

\(a = [M_a,V_a]\)

DUAL QUATERNIONS DEMYSTIFIED

not unique

one element,

two meanings.

not covariant

two elements,

one meaning.

\(M\)

\(M^{-T}\)

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R^3\)

vectors \(\mathbb R^3\)

matrices \(\mathbb R^{3\times3}\)

Points

Directions

Translations

Rotations

Lines

Planes

\([M_{ab},V_{ab}] = [M_aM_b,M_aV_b+V_a]\)

not included

no elements in algebra.

too big

elements w/o meaning

\(a = [M_a,V_a]\)

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R^4\)

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R^4\)

vectors \(\mathbb R^4\)

Points

\((x,y,z,1)\)

Directions

\((x,y,z,0)\)

Lines

Planes

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R^4\)

vectors \(\mathbb R^4\)

matrices \(\mathbb R^{4\times4}\)

Points

\((x,y,z,1)\)

Directions

\((x,y,z,0)\)

Translations

Rotations

Lines

Planes

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R^4\)

vectors \(\mathbb R^4\)

matrices \(\mathbb R^{4\times4}\)

Points

\((x,y,z,1)\)

Directions

\((x,y,z,0)\)

Translations

Rotations

Lines

Planes

\(M_{ab} = M_aM_b\)

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R^4\)

vectors \(\mathbb R^4\)

matrices \(\mathbb R^{4\times4}\)

Translations

Rotations

Lines

Planes

\(M_{ab} = M_aM_b\)

not covariant

two elements,

one meaning.

\(M\)

\(M^{-T}\)

not included

no elements in algebra.

Points

\((x,y,z,1)\)

Directions

\((x,y,z,0)\)

too big

elements w/o meaning/use

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R_{3,0,1}\)

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R_{3,0,1}\)

Lines

Points

(infinite points=directions)

Planes

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R_{3,0,1}\)

Rotations

Lines

Points

(infinite points=directions)

Planes

Translations

(rotations around infinite lines)

+Reflections +Point reflections.

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R_{3,0,1}\)

Rotations

Lines

\(M_{ab} = M_aM_b\)

Points

(infinite points=directions)

Planes

Translations

(rotations around infinite lines)

+Reflections +Point reflections.

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R_{3,0,1}\)

Rotations

Lines

\(M_{ab} = M_aM_b\)

Points

(infinite points=directions)

Planes

✓ all elements included

✓ covariant transforms

✓ just the right size

Translations

(rotations around infinite lines)

+Reflections +Point reflections.

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R_{3,0,1}\)

Rotations

Lines

\(M_{ab} = M_aM_b\)

Points

(infinite points=directions)

Planes

Easy to work out if planes are vectors, no new products needed.

Translations

(rotations around infinite lines)

+Reflections +Point reflections.

✓ all elements included

✓ covariant transforms

✓ just the right size

You're doing things upside down!!

Why must vectors be planes ?

Can't we just invent an anti-product, anti-exponential, anti-logarithm, anti- ... ?

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

\(\mathbb R_{3,0,1}\)

Rotations

Lines

\(M_{ab} = M_aM_b\)

Points

(infinite points=directions)

Planes

Easy to work out if planes are vectors, no new products needed.

You're doing things upside down!!

Why must vectors be planes ?

Can't we just invent an anti-product, anti-exponential, anti-logarithm, anti- ... ?

Translations

(rotations around infinite lines)

+Reflections +Point reflections.

✓ all elements included

✓ covariant transforms

✓ just the right size

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

You're doing things upside down!!

Why must vectors be planes ?

To show we're not doing things upside down, lets do things in reverse (and inside-out) ..

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

You're doing things upside down!!

Why must vectors be planes ?

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
work out how to compose transformations

DUAL QUATERNIONS DEMYSTIFIED

How do we formalize geometry ?

We need a way to move from drawings in the sand to (computer) calculations.

define object representation
work out how these objects transform.
~~work out how to compose transformations~~

Without an object representation, we can't define transformations, and without transformations we can not define composition..

Or can we? Time for life hack 1 ..

DUAL QUATERNIONS DEMYSTIFIED

Turn 30 degrees clockwise:

if we can't describe or transform our objects ..

DUAL QUATERNIONS DEMYSTIFIED

Turn 30 degrees clockwise:

we'll simply

transform our space ..

if we can't describe or transform our objects ..

DUAL QUATERNIONS DEMYSTIFIED

Transform space

Free Covariance !!!!

Turn 30 degrees clockwise:

DUAL QUATERNIONS DEMYSTIFIED

Transform space

How do we formalize geometry ?

identify transformations.
work out composition.
think about objects

We start with an empty bag, and fill it with transformations.

Let's try for the 2D (projective) plane.

Which transformations ?

Transformations that do not stretch, tear or bend the space.

(aka the Euclidean or distance preserving transformations)

DUAL QUATERNIONS DEMYSTIFIED

Our notion of symmetry is based on our notion of equal distances
and/or magnitudes of angles

\( \lVert x, y \rVert = \lVert f(x), f(y) \rVert \)

So we start by looking at the isometries of the projective plane.

That is all maps \(f\) that preserve distances and relative angles.

The bag with all possible \(f\) is called \({E}(2)\), the Euclidean Group in two dimensions.

Transformations of space are also called symmetries.

SYMMETRIES - The Identity

The first symmetry we consider, is the trivial isometry, the Identity map.

If we don't do anything - everything stay the same.

We put the identity in our bag:

SYMMETRIES - The Reflection

One of the first things we think of when we say symmetry is a mirror. The second isometry we consider is the reflection. A mirror preserves distances and angles.

Reflections transform the entire plane, leaving only the points on the mirror in place.
Reflections change handedness - they are called opposite symmetries.
Reflections are discrete symmetries.
Repeating the same reflection twice restores the plane to its original position.

SYMMETRIES - The Rotation

Another isometry is the rotation. Rotating the plane (or space) also leaves

distances and angles unchanged.

Rotations transform the entire plane, leaving only the pivot in place.
Rotations preserve handedness - they are called direct symmetries.
Rotations are a continuous symmetry.

SYMMETRIES - The Translation

Another isometry is the translation. Translating the plane (or space) also leaves

distances and angles unchanged. Does it have fixed, invariant points ?

Translations transform the entire plane, leaving only ... place.
Translations preserve handedness - they are called direct symmetries.
Translations are a continuous symmetry.

SYMMETRIES - Composition

There are still other isometries that we have not included yet.

One example is the glide reflection or transflexion,

New - but clearly a combination of a translation and a reflection.

SYMMETRIES - Composition

Applying two or more isometries allows us to combine our existing isometries into new ones. We will write this using juxtaposition, so that applying isometry \(a\), followed by applying isometry \(b\) is written :

\(c=ba\)

Now we can use the composition of these isometries as building blocks to construct new ones.

Our bag of transformations now has the identy, reflections, rotations, translations and their combinations. Do we now have all isometries?

SYMMETRIES - Composition

Do we now have all isometries ?

SYMMETRIES - Composition

Do we now have all isometries ?

Translation \(t\)

SYMMETRIES - Composition

Do we now have all isometries ?

Translation \(t\)

\( \boldsymbol \circlearrowleft\)

Rotation \(r\)

SYMMETRIES - Composition

Do we now have all isometries ?

Translation \(t\)

\( \boldsymbol \circlearrowleft\)

Rotation \(r\)

Reflection \(m\)

So yes - we can now use reflections, rotations, translations and composition to build all of the possible isometries.

SYMMETRIES - Composition

Can we also break them down?

Maybe some of our elements already are compositions?

Are translations, rotations and reflections all truly fundamental? To find out lets study the composition of two reflections.

SYMMETRIES - Two Reflections

We combine two reflections \(a\) and \(b\) and study the result

if \(a=b\), the reflections cancel out : \[ab = a^2 = b^2 = 1\]

SYMMETRIES - Two Reflections

We combine two reflections \(a\) and \(b\) and study the result

2 identical reflections \(\rightarrow\) identity
if \(a\) and \(b\) intersect, their product \(ab\) is a rotation around the intersection point. (and \(ba\) is the opposite rotation)

SYMMETRIES - Two Reflections

We combine two reflections \(a\) and \(b\) and study the result

2 identical reflections \(\rightarrow\) identity
2 intersecting reflections \(\rightarrow\) rotation
2 parallel reflections \(\rightarrow\) translation

The reflection is our basic building block for Euclidean transformations !

Rotations and Translations are just compositions of reflections

SYMMETRIES - Reflections all the way down.

0 reflections \(\rightarrow\) identity
1 reflection \(\rightarrow\) reflection
2 reflections \(\rightarrow\) rotation, translation
3 reflections \(\rightarrow\) glide/roto reflection
4 reflections ?
5 reflections ?

The reflection is our basic building block for Euclidean transformations !

All Euclidean transformations can be constructed from reflections.

It's reflections all the way down, but how far up does it go?

SYMMETRIES - Closure

\(1\) = identity
\(a\) = reflection
\(ab\) = rotation/translation
\(abc\) = roto-reflection/glide reflection
\(abcd\) = rotation/translation \(\cong ef\)

Cartan-Dieudonne :

Every orthogonal transformation in an n-dimensional symmetric bilinear space can be described as the composition of at most n reflections.

SYMMETRIES - The Euclidean Group

Identity

Reflections

Rotations/Translations

Roto/Glide Reflections

\(1\)

\(a,b,c\)

\(ab, ac, bc\)

\(abc\)

\( {E}(2)\)

Euclidean Group

The Euclidean Group contains all isometries, all distance-preserving transformations.

In many real world problems, we only consider the direct isometries.

These form a sub group of the Euclidean group, called the Special Euclidean Group.

Intuition: Any product of an even number of reflections is even.

SYMMETRIES - The Euclidean Group

Identity

Reflections

Rotations/Translations

Roto/Glide Reflections

\(1\)

\(a,b,c\)

\(ab, ac, bc\)

\(abc\)

\( {E}(2)\)

Euclidean Group

\(1\)

\(ab, ac, bc\)

Identity

Rotations/Translations

\( {SE}(2)\)

Special Euclidean Group

The Special Euclidean Group still contains all rotations for all points.

if \(ab\) rotates \(1\degree\), then \((ab)^2\) rotates \(2\degree\) and \((ab)^x=e^{\ln(ab)x}\) rotates \(x\degree\)

With the exponential map, we can make a bag with one rotation for all points

This (linear = we can scale and add angles) bag is called the Lie Algebra

SYMMETRIES - The Euclidean Group

Identity

Reflections

Rotations/Translations

Roto/Glide Reflections

\(1\)

\(a,b,c\)

\(ab, ac, bc\)

\(abc\)

\({E}(2)\)

Euclidean Group

\(ab, ac, bc\)

only combinations of 2 orthogonal reflections

\(\mathfrak {se}(2)\)

Special Euclidean Algebra

Considering only one rotation per point. (reconstruct others with exponential map)

\(1\)

\(ab, ac, bc\)

Identity

Rotations/Translations

\({SE}(2)\)

Special Euclidean Group

in GA, these are pure bivectors.

Considering only the direct isometries. (GA: even subalgebra, LA: +1 determinant)

SYMMETRIES - Recap.

Identity

Reflections

Rotations/Translations

Roto/Glide Reflections

\(1\)

\(a,b,c\)

\(ab, ac, bc\)

\(abc\)

\(M_{ab} = M_aM_b\)

How do we formalize geometry ?

identify transformations.
work out composition.
think about objects

So we're looking for points, lines and planes..

Searching for Geometry.

# Reflections

2D Invariant

plane

line

point

3D Invariant

volume

plane

line

point

Transformations of \( \mathfrak E(n)\) already strong link with geometric elements !

Searching for Geometry.

2D Invariant

plane

line

point

3D Invariant

volume

plane

line

point

Transformations of \( E(n)\) already strong link with geometric elements !

Use a reflection to represent a line (2D) and a plane (3D). (easy 1-to-1 map)

We simply identify the geometry with the invariants of the symmetries.

# Reflections

Searching for Geometry.

# Reflections

2D Invariant

plane

line

point

3D Invariant

volume

plane

line

point

Transformations of \( E(n)\) already strong link with geometric elements !

Many rotations keep the same point/line invariant, pick the orthogonal one.

We simply identify the geometry with the invariants of the symmetries.

Use a reflection to represent a line (2D) and a plane (3D). (easy 1-to-1 map)

An algebra of symmetries.

# Reflections

2D Invariant

plane

line

point

line

3D Invariant

volume

plane

line

point

screw axis

2D transform

identity

reflect

rotate translate

roto/glide refl.

3D transform

identity

reflect

rotate translate

point reflect

screw motion

Every product of reflections is both a transformation and an element of the geometry.

Every element is an eigen-element w.r.t. the transformation it represents.

This produces a very elegant algebra, that is coordinate free, dimension-independent, with expressions that are easy to reason about.

An algebra of symmetries.

Every product of reflections is both a transformation and an element of the geometry.

for 3D PGA :

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

\(M_{ab} = M_aM_b\)

Group Composition.

Group Action.

How do we transform the elements?

The Sandwich Hack

How do we transform the elements?

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

To rotate the red line \(\ell\)

How do we transform the elements?

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Sandwich Hack

To rotate the red line \(\ell\)

We first rotate the space with rotation \(ab\)

\(ab\)

How do we transform the elements?

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Sandwich Hack

To rotate the red line \(\ell\)

We first rotate the space with rotation \(ab\)

\(ab\)\(\ell\)

Then we combine with the line \(\ell\)

How do we transform the elements?

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Sandwich Hack

To rotate the red line \(\ell\)

We first rotate the space with rotation \(ab\)

\(ab\)\(\ell\)\(ba\)

Then we combine with the line \(\ell\)

Then we rotate back with rotation \(ba\)

How do we transform the elements?

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Sandwich Hack

To rotate the red line \(\ell\)

\(ab\)\(\ell\)\(ba\)

The sandwich product can transform all elements because it doesn't transform any element.

It is double-sided because we are transforming the space before and after.

How do we transform the elements?

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Sandwich Hack

To rotate the red line \(\ell\)

\(ab\)\(\ell\)\(ba\)

The sandwich product can transform all elements because it doesn't transform any element.

It is double-sided because we are transforming the space before and after.

How do we transform the elements?

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Sandwich Hack

But how do we write these reflections down with numbers ?

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Euclidean Algebra

* \rightarrow \color{blue}ab

\,\color{blue}ab\color{red}x\color{blue}ba\,\,

product = composition

sandwich = action

\({\mathbf e_-}^2=-1\)

\({\mathbf e_+}^2=1\)

\({\mathbf e_0}^2=0\)

But how do we write these reflections down with numbers ?

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Euclidean Algebra

* \rightarrow \color{blue}ab

\,\color{blue}ab\color{red}x\color{blue}ba\,\,

product = composition

sandwich = action

\({\mathbf e_-}^2=-1\)

\({\mathbf e_+}^2=1\)

\({\mathbf e_0}^2=0\)

But how do we write these reflections down with numbers ?

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Euclidean Algebra

* \rightarrow \color{blue}ab

\,\color{blue}ab\color{red}x\color{blue}ba\,\,

product = composition

sandwich = action

\({\mathbf e_+}^2=1\)

\({\mathbf e_0}^2=0\)

But how do we write these reflections down with numbers ?

\({\mathbf e_-}^2=-1\)

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Euclidean Algebra

* \rightarrow \color{blue}ab

\,\color{blue}ab\color{red}x\color{blue}ba\,\,

product = composition

sandwich = action

But how do we write these reflections down with numbers ?

Write homogeneous linear equations as linear combinations of three Euclidean mirrors \(\mathbf e_1, \mathbf e_2, \mathbf e_3\) and one mirror at infinity \(\mathbf e_0\)

\({\mathbf e_i}^2=1\)

\({\mathbf e_0}^2=0\)

\(\mathbf e_i\mathbf e_j=-\mathbf e_j\mathbf e_i\)

\(a\mathbf x + b\mathbf y + c\mathbf z + d = 0\)

\(a\mathbf e_1 + b\mathbf e_2 + c\mathbf e_3 + d\mathbf e_0\)

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Euclidean Algebra

* \rightarrow \color{blue}ab

\,\color{blue}ab\color{red}x\color{blue}ba\,\,

product = composition

sandwich = action

\(a\mathbf e_1 + b\mathbf e_2 + c\mathbf e_0\)

ok this clearly works to represent a line - does it now also work as reflection ?

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Euclidean Algebra

* \rightarrow \color{blue}ab

\,\color{blue}ab\color{red}x\color{blue}ba\,\,

product = composition

sandwich = action

ok this clearly works to represent a line - does it now also work as reflection ?

\(\mathbf x + \mathbf y + 1 = 0 \rightarrow \mathbf e_1 + \mathbf e_2 + \mathbf e_0\)

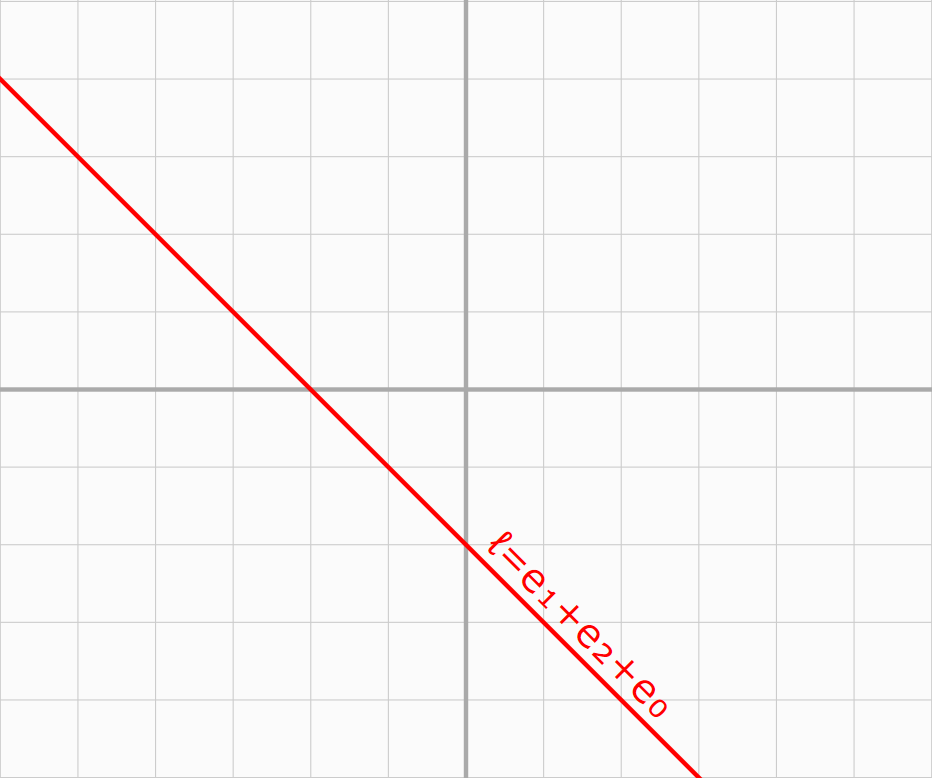
a line \(\ell = \mathbf e_1 + \mathbf e_2 + \mathbf e_0 \)

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Euclidean Algebra

* \rightarrow \color{blue}ab

\,\color{blue}ab\color{red}x\color{blue}ba\,\,

product = composition

sandwich = action

ok this clearly works to represent a line - does it now also work as reflection ?

\(\mathbf x + \mathbf y + 1 = 0 \rightarrow \mathbf e_1 + \mathbf e_2 + \mathbf e_0\)

\(x = 0 \rightarrow \mathbf e_1\)

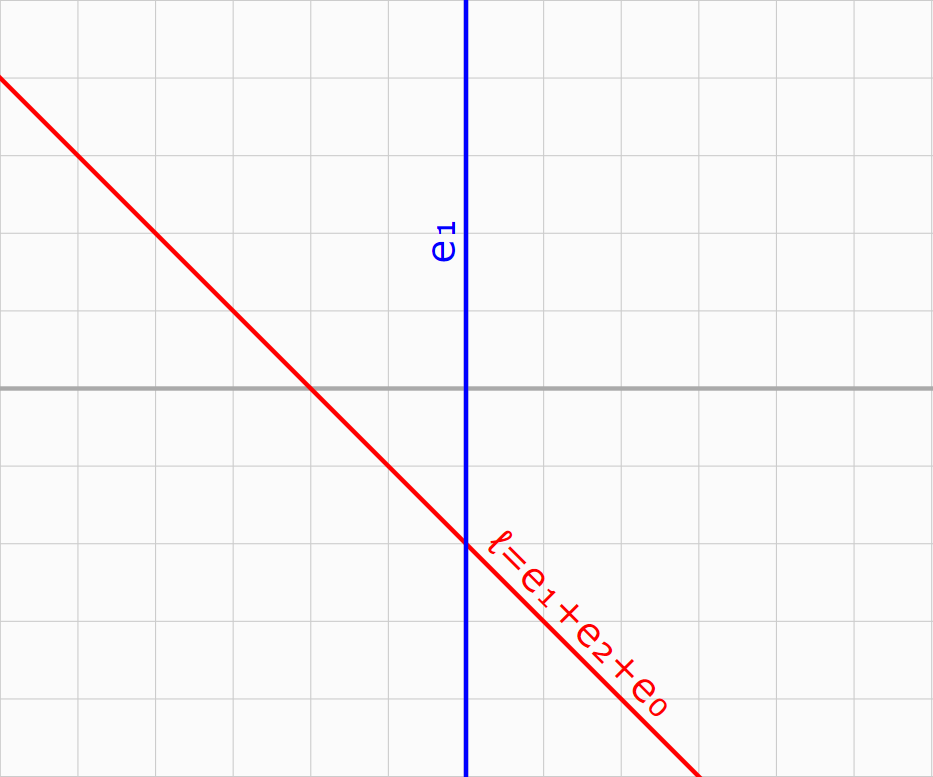
a line \(\ell = \mathbf e_1 + \mathbf e_2 + \mathbf e_0 \)

and a mirror \(\mathbf e_1\)

Identity 1

Reflections a,b,c,d

Rotations/Translations ab,ac,ad,bc,bd,cd

point reflections abc,abd,acd,bcd

screws abcd

planes

lines

points

The Euclidean Algebra

* \rightarrow \color{blue}ab

\,\color{blue}ab\color{red}x\color{blue}ba\,\,

product = composition

sandwich = action

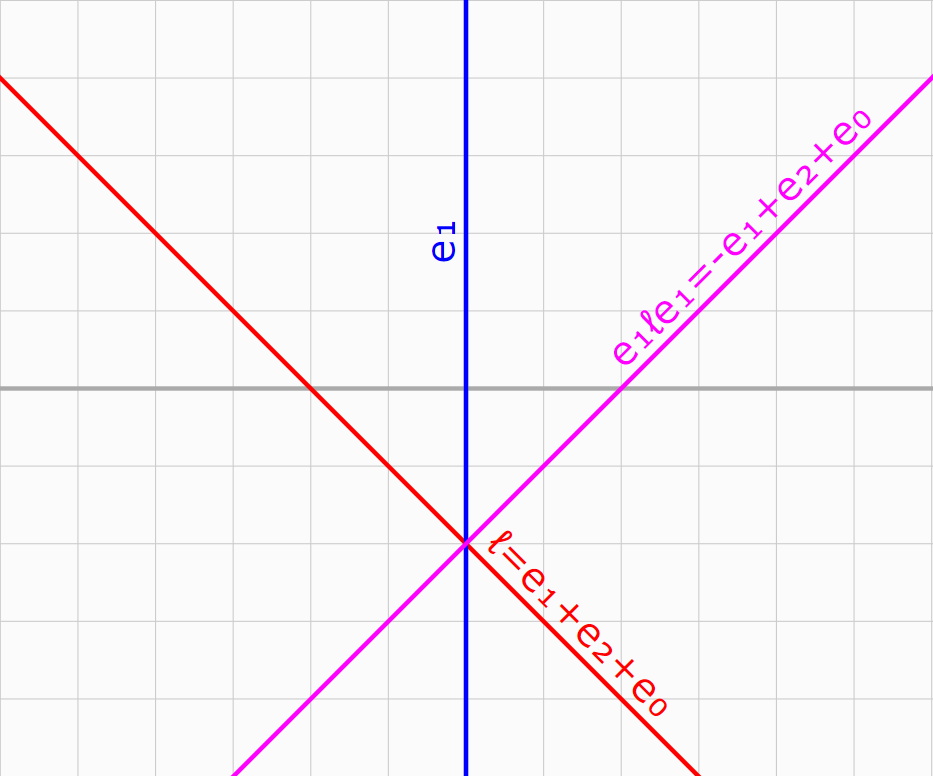
a line \(\ell = \mathbf e_1 + \mathbf e_2 + \mathbf e_0 \)

and a mirror \(\mathbf e_1\)

\(\color{blue}\mathbf e_1\color{black}(\color{red}\mathbf e_1 + \mathbf e_2 + \mathbf e_0\color{black})\color{blue}\mathbf e_1\)
\(= (1 + \mathbf e_{12} - \mathbf e_{01})\mathbf e_1\)
\(= \color{magenta}\mathbf e_1 - \mathbf e_2 - \mathbf e_0\)

Identity

Reflections

Rotations/Translations

point reflections

screws

planes

lines

points

PGA - Projective Geometric Algebra

* \rightarrow \color{blue}ab

\,\color{blue}ab\color{red}x\color{blue}ba\,\,

geometric product = composition

sandwich = action

\(x\mathbf e_{032} + y\mathbf e_{013} + z\mathbf e_{021} + \mathbf e_{123}\)

With the geometric product and planes as vectors - you get an algebra that naturally generates the Euclidean Group!

\(a\mathbf e_1 + b\mathbf e_2 + c\mathbf e_3 + d\mathbf e_0\)

\(d_x\mathbf e_{01}+d_y\mathbf e_{02}+d_z\mathbf e_{03}+x\mathbf e_{23}+y\mathbf e_{31}+z\mathbf e_{12}\)

\begin{aligned} \color{red}\mathbf e_i^2 &= +1 \\ \color{green}\mathbf e_0^2 &= 0 \\ \color{black}\mathbf e_i\mathbf e_j&=-\mathbf e_j\mathbf e_i \end{aligned}

Identity

Reflections

Rotations/Translations

point reflections

screws

planes

lines

points

PGA - Projective Geometric Algebra

* \rightarrow \color{blue}ab

\,\color{blue}ab\color{red}x\color{blue}ba\,\,

geometric product = composition

sandwich = action

\(x\mathbf e_{032} + y\mathbf e_{013} + z\mathbf e_{021} + \mathbf e_{123}\)

With the geometric product and planes as vectors - you get an algebra that naturally generates the Euclidean Group!

\(a\mathbf e_1 + b\mathbf e_2 + c\mathbf e_3 + d\mathbf e_0\)

\(d_x\mathbf e_{01}+d_y\mathbf e_{02}+d_z\mathbf e_{03}+x\mathbf e_{23}+y\mathbf e_{31}+z\mathbf e_{12}\)

Homogeneous Linear Equation

Plucker Coordinates

Homogeneous Point

\begin{aligned} \color{red}\mathbf e_i^2 &= +1 \\ \color{green}\mathbf e_0^2 &= 0 \\ \color{black}\mathbf e_i\mathbf e_j&=-\mathbf e_j\mathbf e_i \end{aligned}

a \cdot b = \langle ab \rangle_{\lvert s-t \rvert}

a \wedge b = \langle ab \rangle_{s+t}

Visualizing PGA

its good to have a visual on how basic operations work.
the visual you are used to uses vectors for everything.
great for visualizing vector addition

not the ideal view for PGA.

We want to visualize :

Geometric product
Inner product
Regressive product
Outer product
Points,Lines,Planes
Reflections,Rotations,Translations

Visualizing PGA : The Elements

Vectors = Lines

\(a\mathbf e_1 + b\mathbf e_2 +c\mathbf e_0\)

Bivectors = Points

\(x\mathbf e_{02} + y\mathbf e_{01} + w\mathbf e_{12}\)

Rotations

\(e^{\frac \alpha 2 (x\mathbf e_{02} + y\mathbf e_{01} + w\mathbf e_{12})}\)

Translations

\(e^{\frac d 2 (x\mathbf e_{02} + y\mathbf e_{01})}\)

Line = Vector

Point = Bivector

Translation

Rotation

Visualizing PGA : The Elements

Line = Vector

Point = Bivector

Translation

Rotation

Vectors = Reflections = Lines

\(a\mathbf e_1 + b\mathbf e_2 +c\mathbf e_0\)

Bivectors = \(\perp\) Reflections = Points

\(x\mathbf e_{02} + y\mathbf e_{01} + w\mathbf e_{12}\)

Intersecting Reflections = Rotations

\(e^{\frac \alpha 2 (x\mathbf e_{02} + y\mathbf e_{01} + w\mathbf e_{12})}\)

Parallel Reflections = Translations

\(e^{\frac d 2 (x\mathbf e_{02} + y\mathbf e_{01})}\)

Points are bivectors
bivectors are compositions of orthogonal reflections
we can rotate these while keeping them orthogonal
rotate so that two mirrors align
twice the same mirror is identity
the geometric product eliminates identical mirrors
the product of two points is twice the translation between them

Visualizing PGA : The Geometric Product

( \color{red}x_1\color{black}\mathbf e_{20} + \color{red}y_1\color{black}\mathbf e_{01} + \mathbf e_{12} )( \color{blue}x_2\color{black}\mathbf e_{20} + \color{blue}y_2\color{black}\mathbf e_{01} + \mathbf e_{12} ) \\ = \color{red}x_1\color{black}\mathbf e_{01} + \color{red}y_1\color{black}\mathbf e_{20} - \color{blue}x_2\color{black}\mathbf e_{01} - \color{blue}y_2\color{black}\mathbf e_{20} - 1\\ = 1 + (\color{blue}x_2\color{black}-\color{red}x_1\color{black})\mathbf e_{01} + (\color{blue}y_2\color{black}-\color{red}y_1\color{black})\mathbf e_{20}

Points are bivectors
bivectors are compositions of orthogonal reflections
we can rotate these while keeping them orthogonal
rotate so that mirrors are orthogonal
the inner product retains orthogonal mirrors
the inner product of a point and a line is a line through the point, orthogonal to the line.

Visualizing PGA : The Inner Product

( \color{red}x\color{black}\mathbf e_{20} + \color{red}y\color{black}\mathbf e_{01} + \mathbf e_{12} )\cdot( \color{blue}a\color{black}\mathbf e_{1} + \color{blue}b\color{black}\mathbf e_{2} + \color{blue}c\color{black}\mathbf e_{0} ) \\ = \color{blue}b\color{black} \mathbf e_1 - \color{blue}a\color{black} \mathbf e_2 + (\color{red}y\color{blue}a\color{black} - \color{red}x\color{blue}b\color{black}) \mathbf e_0

Visualizing PGA : The Join / regressive Product

The Geometric Product eliminates identical reflections.

The Inner Product retains

orthogonal reflections.

The Join retains

identical reflections

( \color{red}x_1\color{black}\mathbf e_{20} + \color{red}y_1\color{black}\mathbf e_{01} + \mathbf e_{12} )\vee ( \color{blue}x_2\color{black}\mathbf e_{20} + \color{blue}y_2\color{black}\mathbf e_{01} + \mathbf e_{12} ) \\ = (\color{red}x_1\color{blue}y_2\color{black}-\color{red}y_1\color{blue}x_2\color{black})\mathbf e_0 + (\color{red}y_1\color{black}-\color{blue}y_2\color{black})\mathbf e_1 + (\color{blue}x_2\color{black}-\color{red}x_1\color{black})\mathbf e_2

Visualizing PGA : The Meet / Outer Product

The Geometric Product eliminates identical reflections.

The Join retains

identical reflections

The Meet identifies
orthogonal reflections

\newcommand{\e}[1]{\mathbf e_{#1}} \newcommand{\one}[1]{{\color{red}#1_1\color{black}}} \newcommand{\two}[1]{{\color{blue}#1_2\color{black}}} (\one a \e1 + \one b \e2 + \one c \e0) \wedge (\two a \e1 + \two b \e2 + \two c \e0)\\ = ( \one c \two a - \one a \two c ) \e{01} + ( \one b \two c - \one c \two b) \e{20} + (\one a \two b - \one b \two a) \e{12}

The Inner Product retains

orthogonal reflections.

Allows you to reason about these products !!

Visualizing PGA : The Projection Operator

The Geometric Product eliminates identical reflections.

The Join retains

identical reflections

The Meet identifies
orthogonal reflections

The Inner Product retains

orthogonal reflections.

Allows you to reason about these products !!

Visualizing PGA : Cartan–Dieudonné

The Geometric Product eliminates identical reflections.

The Join retains

identical reflections

The Meet identifies
orthogonal reflections

The Inner Product retains

orthogonal reflections.

Cartan-Dieudonne :

Every orthogonal transformation in an n-dimensional symmetric bilinear space can be described as the composition of at most n reflections.

The Geometric Product eliminates identical reflections.

The Join retains

identical reflections

The Meet identifies
orthogonal reflections

The Inner Product retains

orthogonal reflections.

Infinity!

Visualizing PGA : Cartan–Dieudonné

Cartan-Dieudonne :

Every orthogonal transformation in an n-dimensional symmetric bilinear space can be described as the composition of at most n reflections.

Visualizing PGA : Reflection of a Point

The Geometric Product eliminates identical reflections.

The Join retains

identical reflections

The Meet identifies
orthogonal reflections

The Inner Product retains

orthogonal reflections.

Associativity!

Infinity!

Allows you to reason about these products !!

Visualizing PGA : 3D Geometric Product

The Geometric Product eliminates identical reflections.

The Join retains

identical reflections

The Meet identifies
orthogonal reflections

The Inner Product retains

orthogonal reflections.

Allows you to reason about these products !!

Visualizing PGA : 3D Geometric Product

The Geometric Product eliminates identical reflections.

The Join retains

identical reflections

The Meet identifies
orthogonal reflections

The Inner Product retains

orthogonal reflections.

The Brutal Violation of PGA

Identity

Reflections

Rotations/Translations

point reflections

screws

planes

lines

points

\(\mathbf e_0,\mathbf e_1,\mathbf e_2,\mathbf e_3\)

\(\mathbf e_{01},\mathbf e_{02},\mathbf e_{03},\mathbf e_{12},\mathbf e_{31},\mathbf e_{23}\)

\(\mathbf e_{021},\mathbf e_{013},\mathbf e_{032},\mathbf e_{123}\)
\(\mathbf e_{0123}\)

The Brutal Violation of PGA

Identity

Reflections

Rotations/Translations

point reflections

screws

planes

lines

points

\(\mathbf e_0,\mathbf e_1,\mathbf e_2,\mathbf e_3\)

\(\mathbf e_{01},\mathbf e_{02},\mathbf e_{03},\mathbf e_{12},\mathbf e_{31},\mathbf e_{23}\)

\(\mathbf e_{021},\mathbf e_{013},\mathbf e_{032},\mathbf e_{123}\)
\(\mathbf e_{0123}\)

The Brutal Violation of PGA

Identity

Rotations/Translations

screws

lines

\(\mathbf e_{01},\mathbf e_{02},\mathbf e_{03},\mathbf e_{12},\mathbf e_{31},\mathbf e_{23}\)

\(\mathbf e_{0123}\)

No longer a representation for planes and points.

Patch : Lines have 3 coefficients that transform like points, and 3 that transform like directions.

The Dual Quaternions

\(\mathbf e_{01},\mathbf e_{02},\mathbf e_{03},\mathbf e_{12},\mathbf e_{31},\mathbf e_{23}\)

\(\mathbf e_{0123}\)

No longer a representation for planes and points.

Patch : Lines have 3 coefficients that transform like points, and 3 that transform like directions.

\(1\)

\(\mathbf e_{12}\)

\(\mathbf e_{31}\)

\(\mathbf e_{23}\)

\(\mathbf e_{01}\)

\(\mathbf e_{02}\)

\(\mathbf e_{03}\)

\(\mathbf e_{0123}\)

Still obviously a combination of an even number of reflections.

Very suitable for carving.

Will take 100 years to decode.

The Dual Quaternions

\(\mathbf e_{01},\mathbf e_{02},\mathbf e_{03},\mathbf e_{12},\mathbf e_{31},\mathbf e_{23}\)

\(\mathbf e_{0123}\)

No longer a representation for planes and points.

Patch : Lines have 3 coefficients that transform like points, and 3 that transform like directions.

\(1\)

\(\mathbf e_{12}\)

\(\mathbf e_{31}\)

\(\mathbf e_{23}\)

\(\mathbf e_{01}\)

\(\mathbf e_{02}\)

\(\mathbf e_{03}\)

\(\mathbf e_{0123}\)

Still obviously a combination of an even number of reflections.

Patch : Rename to hide the internal structure completely.

\(1\)

\(\mathbf i\)

\(\mathbf j\)

\(\mathbf k\)

\(\mathbf {\epsilon i}\)

\(\mathbf {\epsilon j}\)

\(\mathbf {\epsilon k}\)

\(\mathbf {\epsilon}\)

Very suitable for carving.

Will take 100 years to decode.

The Dual Quaternions

\(\mathbf e_{01},\mathbf e_{02},\mathbf e_{03},\mathbf e_{12},\mathbf e_{31},\mathbf e_{23}\)

\(\mathbf e_{0123}\)

No longer a representation for planes and points.

Patch : Lines have 3 coefficients that transform like points, and 3 that transform like directions.

\(1\)

\(\mathbf e_{12}\)

\(\mathbf e_{31}\)

\(\mathbf e_{23}\)

\(\mathbf e_{01}\)

\(\mathbf e_{02}\)

\(\mathbf e_{03}\)

\(\mathbf e_{0123}\)

Still obviously a combination of an even number of reflections.

Patch : Rename to hide the internal structure completely.

\(1\)

\(\mathbf i\)

\(\mathbf j\)

\(\mathbf k\)

\(\mathbf {\epsilon i}\)

\(\mathbf {\epsilon j}\)

\(\mathbf {\epsilon k}\)

\(\mathbf {\epsilon}\)

Very suitable for carving.

Will take 100 years to decode.

The Dual Quaternions

\(\mathbf e_{01},\mathbf e_{02},\mathbf e_{03},\mathbf e_{12},\mathbf e_{31},\mathbf e_{23}\)

\(\mathbf e_{0123}\)

Patch : Lines have 3 coefficients that transform like points, and 3 that transform like directions.

\(1\)

\(\mathbf e_{23}\)

\(\mathbf e_{31}\)

\(\mathbf e_{12}\)

\(\mathbf e_{01}\)

\(\mathbf e_{02}\)

\(\mathbf e_{03}\)

\(\mathbf e_{0123}\)

Patch : Rename to hide the internal structure completely.

\(1\)

\(-\mathbf k\)

\(-\mathbf j\)

\(-\mathbf i\)

\(\mathbf {\epsilon i}\)

\(\mathbf {\epsilon j}\)

\(\mathbf {\epsilon k}\)

\(-\mathbf {\epsilon}\)

Unpatch: Rename to reveal the internal structure.

💡

Unpatch: Use PGA lines to create dquats

product of intersecting lines = rotation
product of parallel lines = translation

}

The Dual Quaternions

\(\mathbf e_{01},\mathbf e_{02},\mathbf e_{03},\mathbf e_{12},\mathbf e_{31},\mathbf e_{23}\)

\(\mathbf e_{0123}\)

Patch : Lines have 3 coefficients that transform like points, and 3 that transform like directions.

Patch : Rename to hide the internal structure completely.

Unpatch: Rename to reveal the internal structure.

💡

}

\(\mathbb H\)

}

\(\mathbb C\)

\(1\)

\(\mathbf e_{23}\)

\(\mathbf e_{31}\)

\(\mathbf e_{12}\)

\(\mathbf e_{01}\)

\(\mathbf e_{02}\)

\(\mathbf e_{03}\)

\(\mathbf e_{0123}\)

\(1\)

\(-\mathbf k\)

\(-\mathbf j\)

\(-\mathbf i\)

\(\mathbf {\epsilon i}\)

\(\mathbf {\epsilon j}\)

\(\mathbf {\epsilon k}\)

\(-\mathbf {\epsilon}\)

Unpatch: Use PGA lines to create dquats

product of intersecting lines = rotation
product of parallel lines = translation

Recap.

Several important symmetry groups have direct Clifford representations.

Each of these has a natural, invariant association with geometry.

\( E(2)\)

\( E(3)\)

Reflections, Rotations, Translations, Rotoreflections, screws

Planes, Lines, Points

Planar Quaternions

Dual Quaternions

\(\mathbb R_{2,0,1}\)

\(\mathbb R_{3,0,1}\)

\( SE(2)\)

\( SE(3)\)

Recap.

Several important symmetry groups have direct Clifford representations.

Each of these has a natural, invariant association with geometry.

\( O(2)\)

\( O(3)\)

\( E(2)\)

\( E(3)\)

Reflections,

Rotations

through origin.

Reflections, Rotations, Translations, Rotoreflections, screws

Planes and Lines through origin + origin.

Planes, Lines, Points

\( SO(2)\)

\( SO(3)\)

\( SE(2)\)

\( SE(3)\)

complex numbers

Quaternions

Planar Quaternions

Dual Quaternions

\(\mathbb R_2\)

\(\mathbb R_3\)

\(\mathbb R_{2,0,1}\)

\(\mathbb R_{3,0,1}\)

Recap.

Several important symmetry groups have direct Clifford representations.

Each of these has a natural, invariant association with geometry.

\( O(2)\)

\( O(3)\)

\( E(2)\)

\( E(3)\)

Reflections,

Rotations

through origin.

Reflections, Rotations, Translations, Rotoreflections, screws

Planes and Lines through origin + origin.

Planes, Lines, Points

\( SO(2)\)

\( SO(3)\)

\( SE(2)\)

\( SE(3)\)

complex numbers

Quaternions

Planar Quaternions

Dual Quaternions

\(\mathbb R_2\)

\(\mathbb R_3\)

\(\mathbb R_{2,0,1}\)

\(\mathbb R_{3,0,1}\)

\(\mathbb R_{3,1}\)

conformal(2)

conformal(3)

\(\mathbb R_{4,1}\)

Inversions,

All conformal Transformations.

Planes, Spheres, Lines, Circles, Point Pairs, Points

\(\mathbb R_{1,3}\)

Lorentz

Refl., Rot., Tran, Boosts

Conformal Geometric Algebra

Works exactly the same way, we simply replace our reflections in lines/planes with reflections in circles/spheres (inversions).

Circle/Sphere with zero radius = point !!

Circle/Sphere with \(\infty\) radius = line/plane !!

Even #reflections = All direct conformal transformations !

Conformal Geometric Algebra

Works exactly the same way, we simply replace our reflections in lines/planes with reflections in circles/spheres (inversions).

Circle/Sphere with zero radius = point !!

Circle/Sphere with \(\infty\) radius = line/plane !!

Even #reflections = All direct conformal transformations !

Can I use this in my game engine ?

YES !

Jeremy Ong's Klein library is an SSE 4.2 optimized production ready C++ PGA implementation that beats the dquat implementations in GLM and similar ..

https://github.com/jeremyong/Klein

Thank You !

There is a short break and follow-up workshop for questions ..

Be sure to join the talks of Dr Dorst on the links with linear algebra this afternoon.

(and those tomorrow and Friday - even if not your field of expertise,
experience what a unified language really means ..)