{GAME23}
GAME23 Sneak Peek
Martin Roelfs, PhD
Lattice Quantum Chromodynamics @ KULAK
GAME23 Sneak Peek
Martin Roelfs

Overview:
- Part 1: An Algebra of Geometry
- Part 2: Implementing the Algebra of Geometry
- Part 3: Closing statements
- Part 4: Visit to the ganja.js Coffeeshop
{GAME23}
{Part 1}
An Algebra of Geometry
{Computer Geometry/Physics}
An Algebra for Geometry
Martin Roelfs

// construct lines
line_from_points (p1, p2)
line_from_points_and_dir (p, d)
line_from_plucker (a, b, c, d, e, f)
// construct planes
plane_from_points (p1, p2, p3)
plane_from_point_and_dirs (p, d1, d2)
plane_from_points_and_dir (p1, p2, d)
plane_from_point_and_line (p, l)
plane_from_equation (a, b, c, d)
// Intersections
intersect_line_plane (l, P)
intersect_plane_plane (P1, P2)
intersect_planes (P1, P2, P3)
// Projections
project_point_plane (p, P)
project_line_plane (l, P)
project_point_line (p, l)// construct transformations
mtx_translate (x, y, z)
mtx_rotate_euler (h, p, b)
mtx_rotate_axis_angle (x, y, z, a)
mtx_look_at (from, too, pole)
// apply transformations
transform_point (M, p)
transform_direction (M, d)
transform_line (M, l)
transform_plane (M, P)




Current state of affairs: linear algebra representation of geometry.
-
Use multiple bags of real numbers and do all bookkeeping ourselves.
- No inherent geometry in matrices.
- Results in a different function for each distinct operation. (Just a subset shown here.)
- Tied to a particular number of dimensions
{Computer Geometry}
An Algebra for Geometry
Martin Roelfs

Wouldn't it be better if we had a single bag of numbers, where each element in this bag is an element of geometry?
Transform \(a\) by \(b\):
Project \(a\) onto \(b\):

(Projective) Geometric Algebra
Teaser: let \(a\) and \(b\) be any elements of geometry (points, lines, planes, translation, rotations, etc)
- Mathematical operations such as multiplication and addition are always geometrically meaningful
- Not tied to a particular number of dimensions




{GA}
An Algebra for Geometry
Martin Roelfs

The idea of Geometric Algebra in just 30 minutes.
- Not just a new way to shuffle coordinates.
- Not just rewriting without cross product.
- Not just the quotient of the tensor algebra with some ideal.
- Not just the extension of vector algebra to multivectors.
+
+
scalar
vector
bivector

The idea of Geometric Algebra in just 30 mins.
- Start from a simple example and Vector Algebra solution
- Inspect that method and highlight some issues
- Introduce the Geometric Algebra approach
- Inspect that method and explore some of the consequences
A simple example ..
\(d_i = \big ( \frac 1 f - \frac 1 {d_0} \big )^{-1}\qquad h_i=-\frac {d_i} {d_0} h_0\)
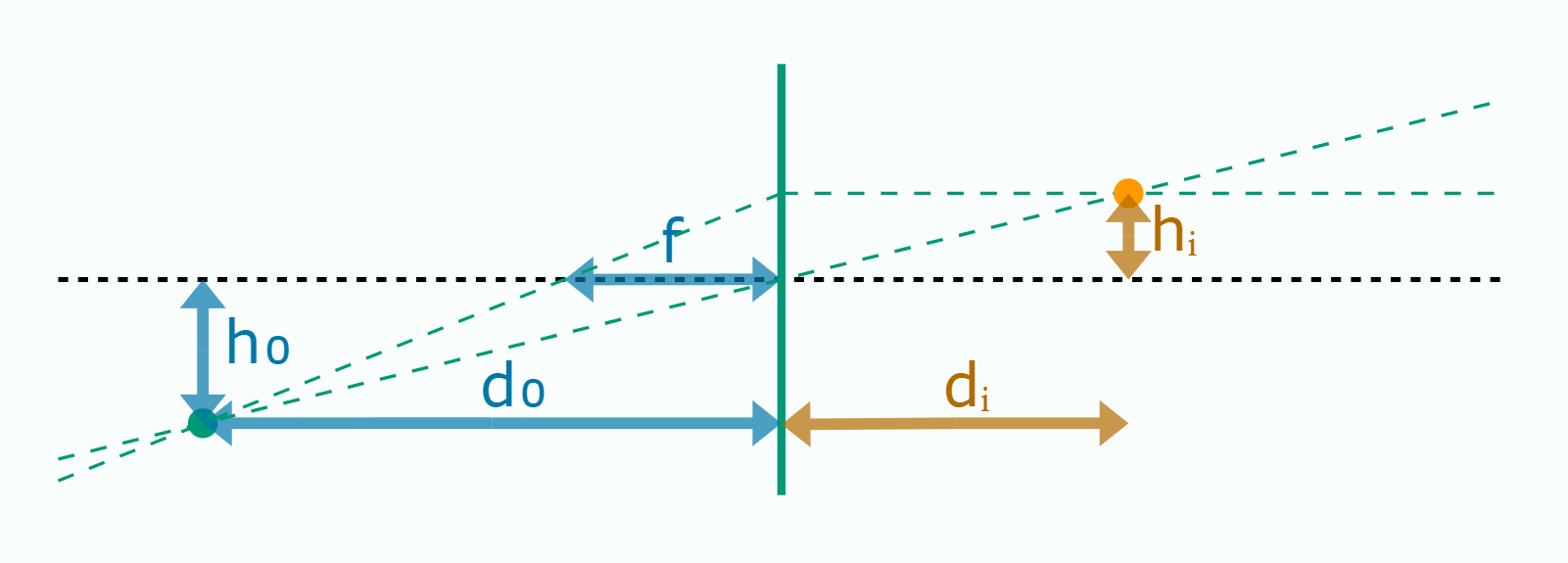
Martin Roelfs
An Algebra for Geometry
{GA}

The idea of Geometric Algebra in just 30 mins.
- Start from a simple example and Vector Algebra solution
- Inspect that method and highlight some issues
- Introduce the Geometric Algebra approach
- Inspect that method and explore some of the consequences
\(d_i = \big ( \frac 1 f - \frac 1 {d_0} \big )^{-1}\qquad h_i=-\frac {d_i} {d_0} h_0\)

The paraxial approximation of the thin lens equation
Martin Roelfs
An Algebra for Geometry
{GA}

\(d_i = \big ( \frac 1 f - \frac 1 {d_0} \big )^{-1}\qquad h_i=-\frac {d_i} {d_0} h_0\)

The paraxial approximation of the thin lens equation
\(\vec a = \overline {\vec c - \vec f}\)
\(\vec b= \vec c - \vec p\)
\(d_0 = \vec a \cdot \vec b\)
Martin Roelfs
An Algebra for Geometry
{GA}

\(d_i = \big ( \frac 1 f - \frac 1 {d_0} \big )^{-1}\qquad h_i=-\frac {d_i} {d_0} h_0\)

The paraxial approximation of the thin lens equation
\((\overline {\vec c - \vec f}) \, \cdot\)
\((\vec c - \vec p)\)
\(d_0 = \)
\(h_0 = (\overline{\vec c - \vec g} )\,\cdot\,(\vec c - \vec p) \)
Martin Roelfs
An Algebra for Geometry
{GA}

The Geometry of Arrows and its Algebra.
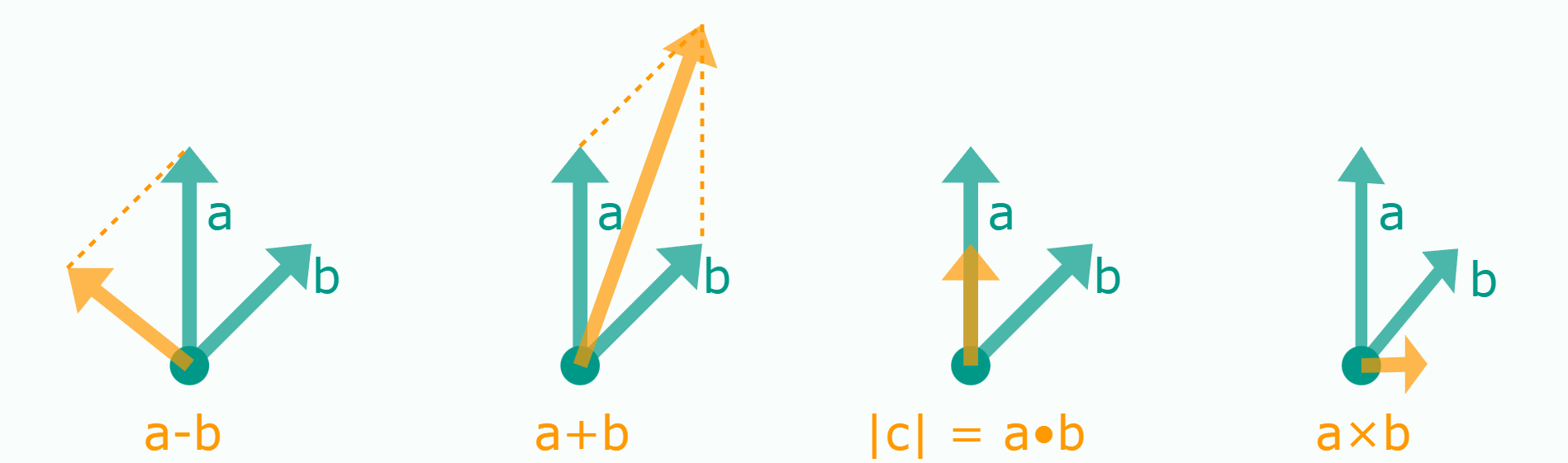
Given the green arrows, all operations are well defined.
Martin Roelfs
An Algebra for Geometry
{GA}

The Geometry of Arrows and its Algebra.
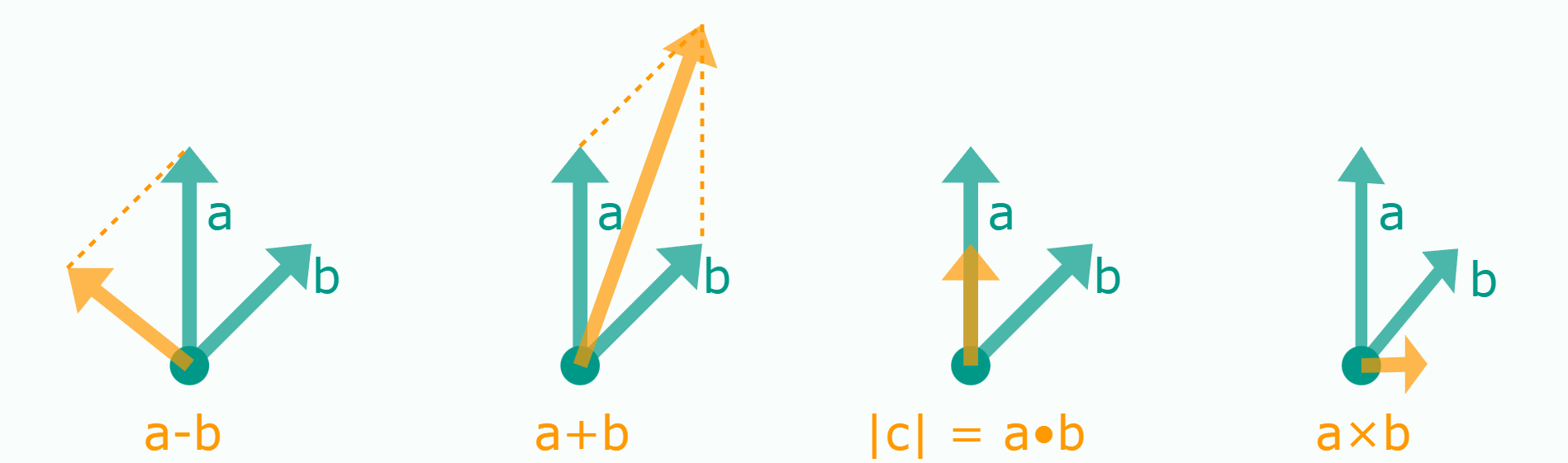
Given the green arrows, all operations are well defined.
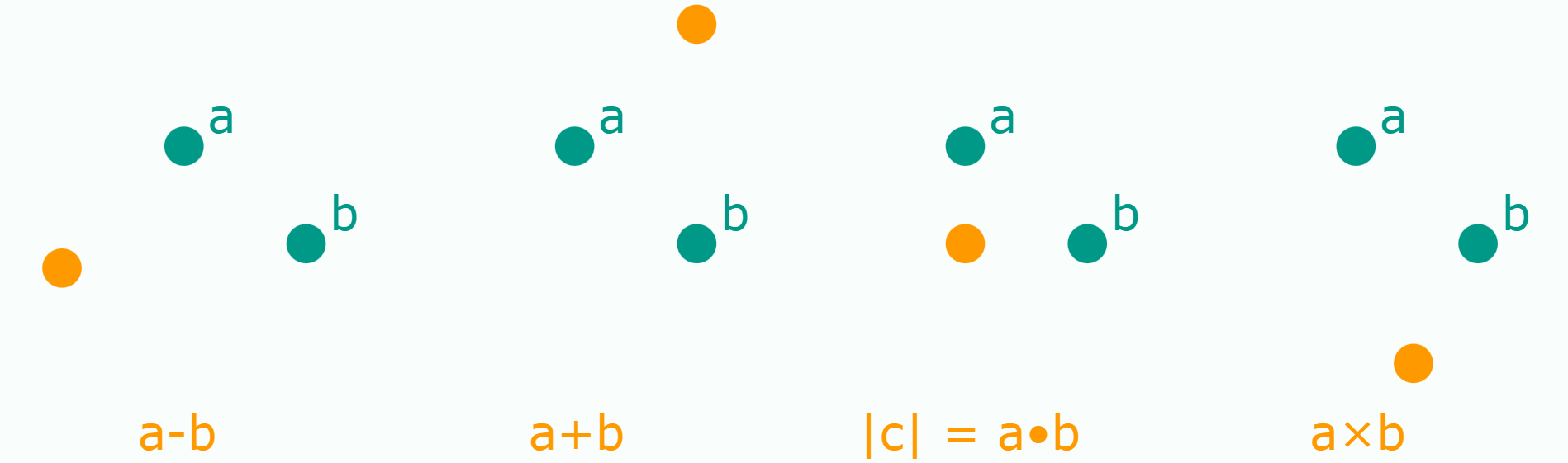
Given the green points, no operation makes geometric sense.
Euclid's first postulate : two points determine a single line.
(and nothing else!)
Martin Roelfs
An Algebra for Geometry
{GA}

The Geometry of Arrows and its Algebra.
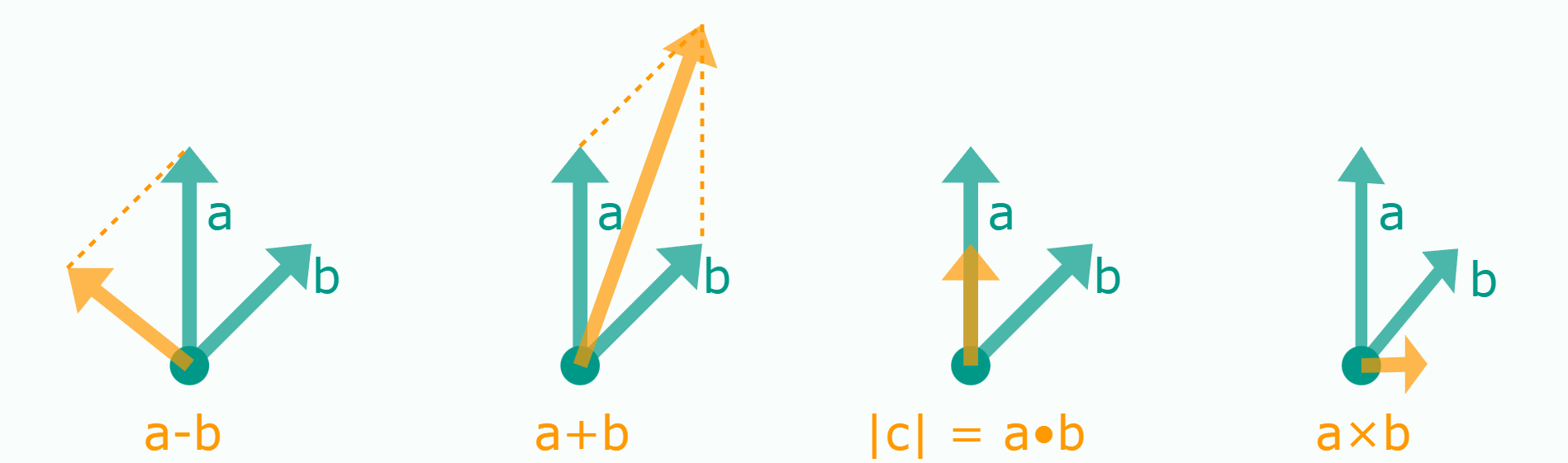
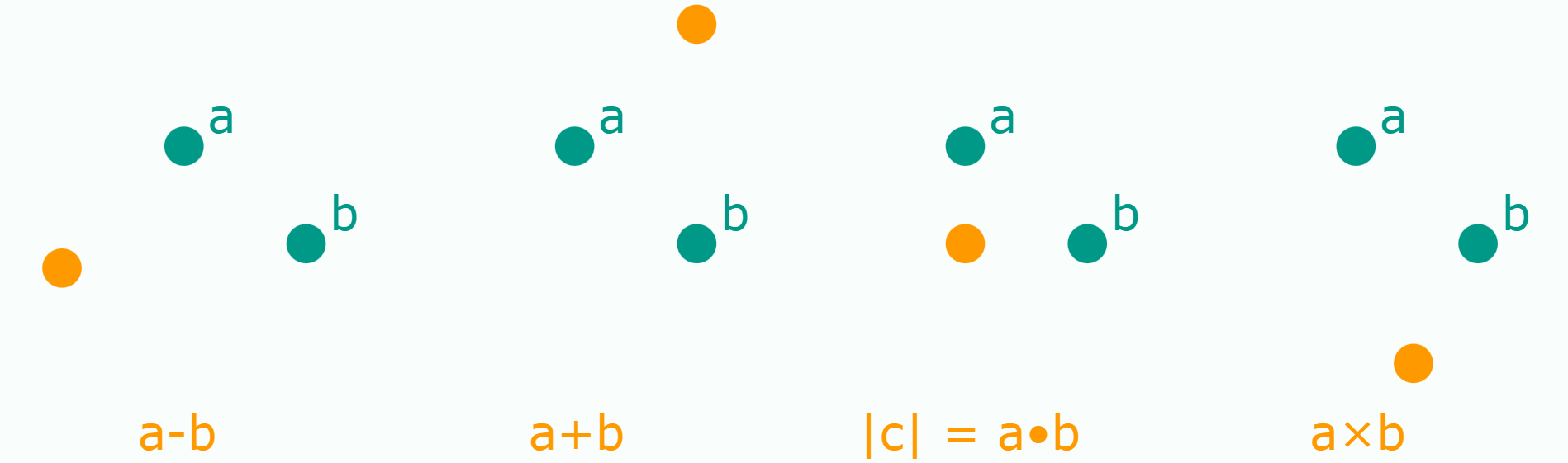
For any operation \(\circ\) between two points to be geometric, its result must be in the 1D line they span!
(that's addition, subtraction, all products ...)
Martin Roelfs
An Algebra for Geometry
{GA}

The Geometry of Arrows and its Algebra.
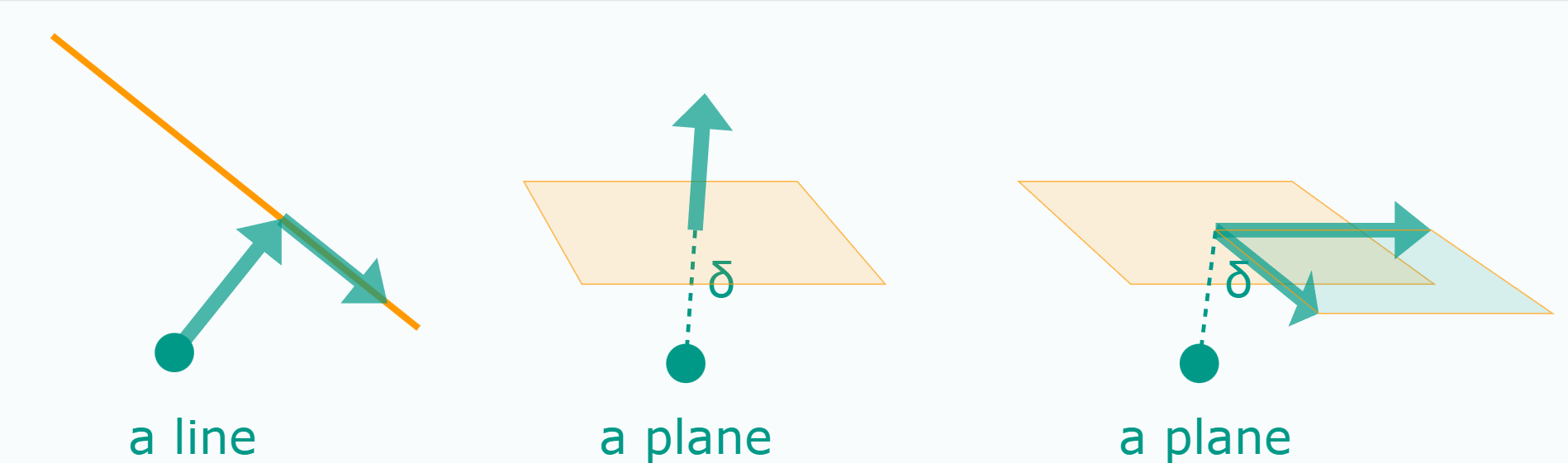
Lines and Planes are even more problematic, and can not trivially be mapped to arrows or multi-arrows.
Martin Roelfs
An Algebra for Geometry
{GA}

The Geometry of Arrows and its Algebra.
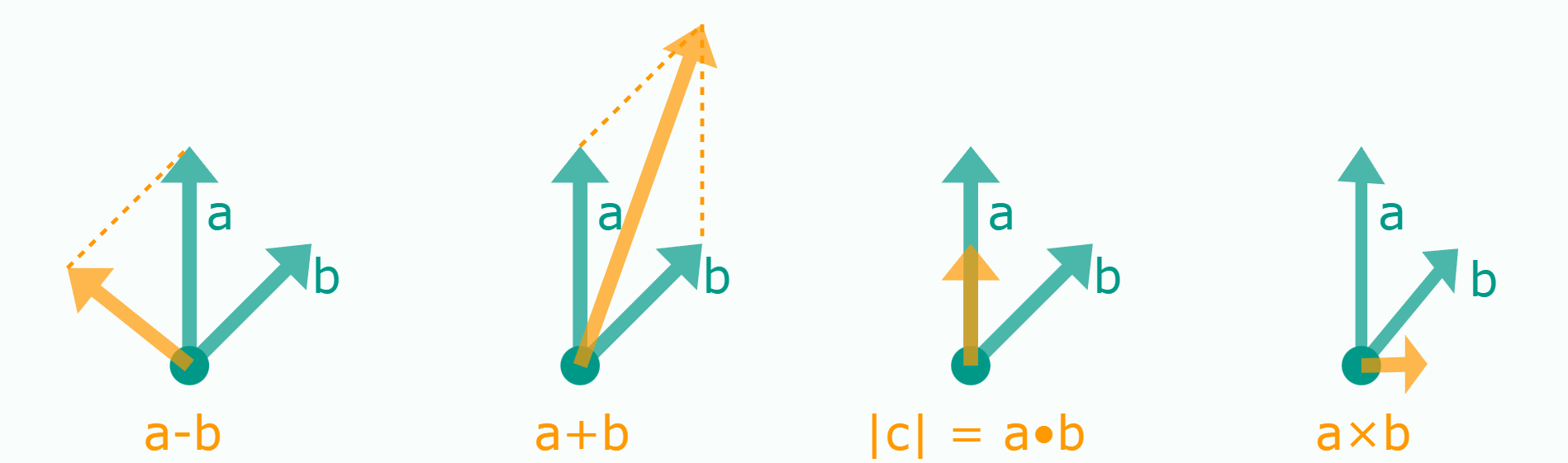
- Vector Algebra is a perfect match for Arrow Geometry
- Less ideal for points/lines/planes
How can we improve this?
Martin Roelfs
An Algebra for Geometry
{GA}

Homogeneous/Projective Coordinates

- Fundamental building block of CG
- Projective arrows solve addition of points
- Dot and Cross product not in subspace
- Projective multiarrows for lines/planes..
- Addition/Subtraction become geometric
- Typical first GA approach
- Addition and Subtraction regain geometric meaning
- Results are independent of origin, but visualisation is not!
- A dimension of intuition is sacrificed
Martin Roelfs
An Algebra for Geometry
{GA}

For the geometry of points, lines, planes ..
- All operations work in the subspace of their arguments
- Represent all elements AND transformations within the same algebra
Instead of an algebra of arrows,
we use an algebra build from reflections.
k-reflections
Geometric Gauges
Martin Roelfs
An Algebra for Geometry
{GA}

k-reflections
Geometric Gauges
- If \( a= b\), the reflections cancel out: \(a^2 = b^2 = \pm 1\).
- If \(a\) and \(b\) intersect, the result is a rotation around their intersection point
- If \(a\) and \(b\) are parallel, the resul is a translation
Martin Roelfs
An Algebra for Geometry
{GA}

k-reflections
Geometric Gauges
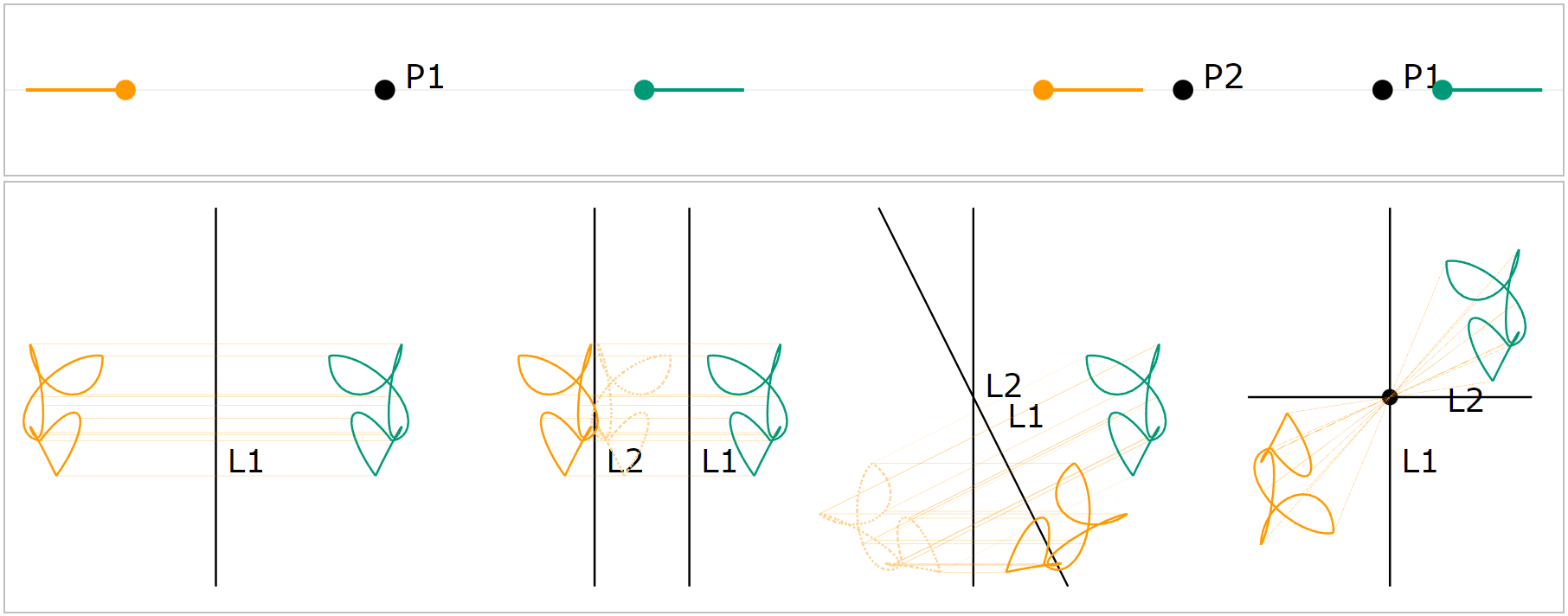
Elements = Transformations = k-Reflections
Martin Roelfs
An Algebra for Geometry
{GA}

k-reflections
Geometric Gauges
Each k-reflection (with k>1) can be gauged without changing the result.
Martin Roelfs
An Algebra for Geometry
{GA}

k-reflections
Geometric Gauges
Each k-reflection (with k>1) can be gauged without changing the result.
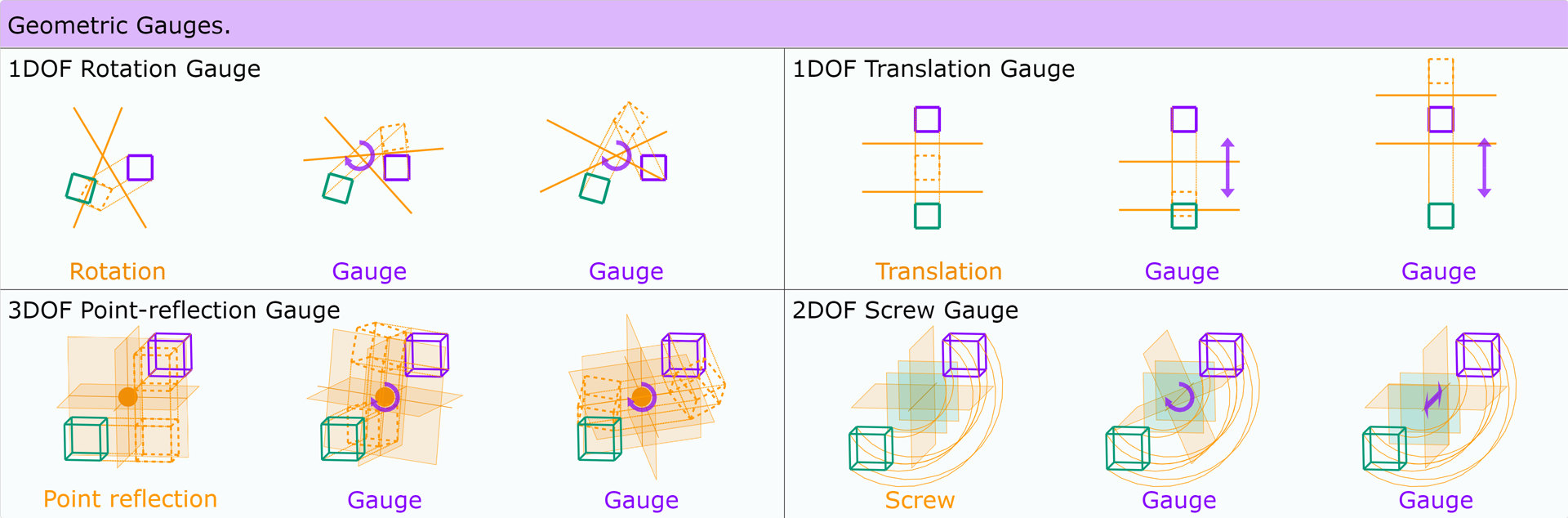
Martin Roelfs
An Algebra for Geometry
{GA}

Gauges tell us how reflections combine!
Cartan-Dieudonné
Every orthogonal transformation in an n-dimensional embedding space
is composed from at most n reflections
Martin Roelfs
An Algebra for Geometry
{GA}

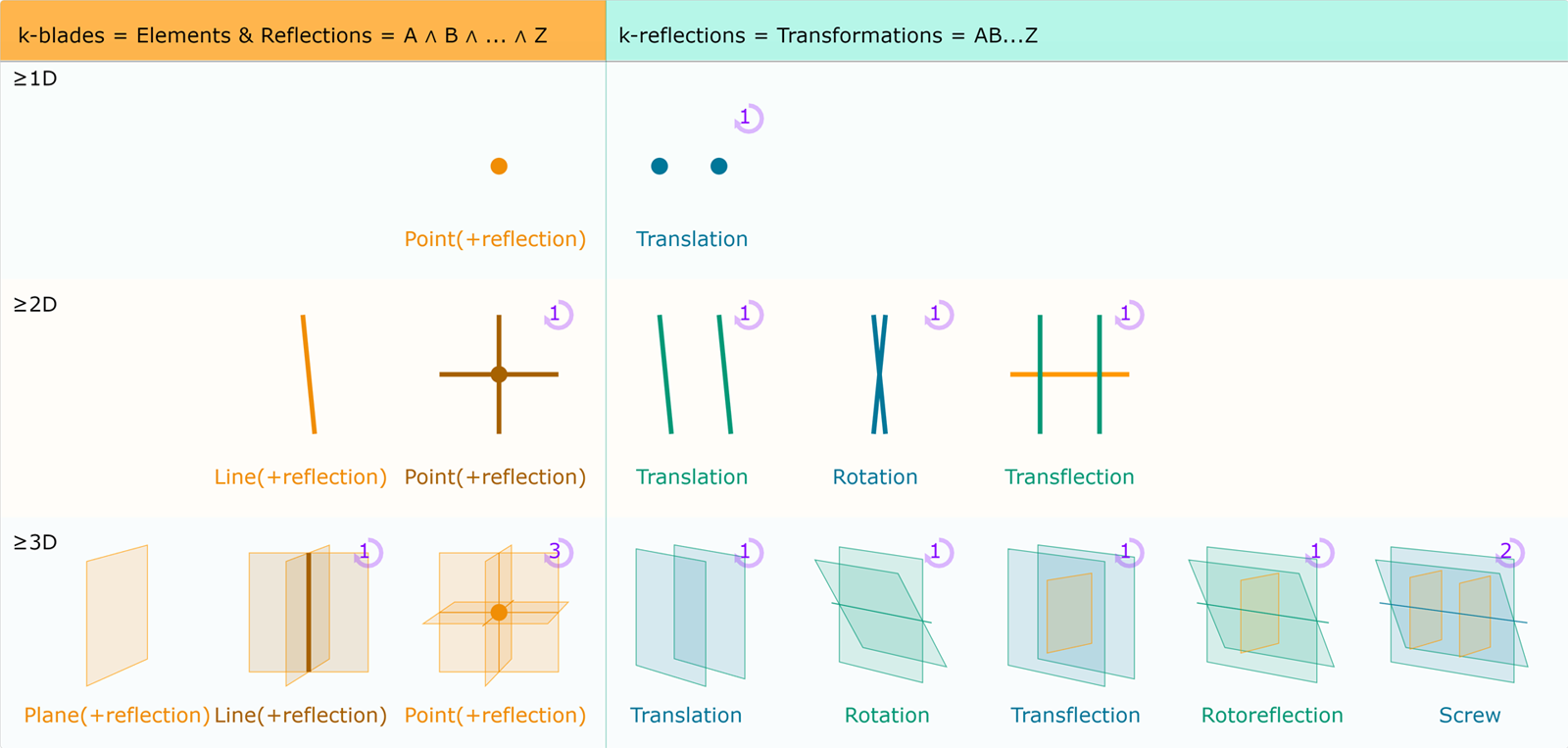
This flavor of GA is called PGA.
Martin Roelfs
An Algebra for Geometry
{GA}


\(ab\) Geometric Product composes reflections
Martin Roelfs
An Algebra for Geometry
{GA}

\(a\wedge b\) Outer Product Intersects elements
Martin Roelfs
An Algebra for Geometry
{GA}

\(a\vee b\) Regressive Product joins elements
Martin Roelfs
An Algebra for Geometry
{GA}

\(a\cdot b\) Dot Product rejects elements
Martin Roelfs
An Algebra for Geometry
{GA}

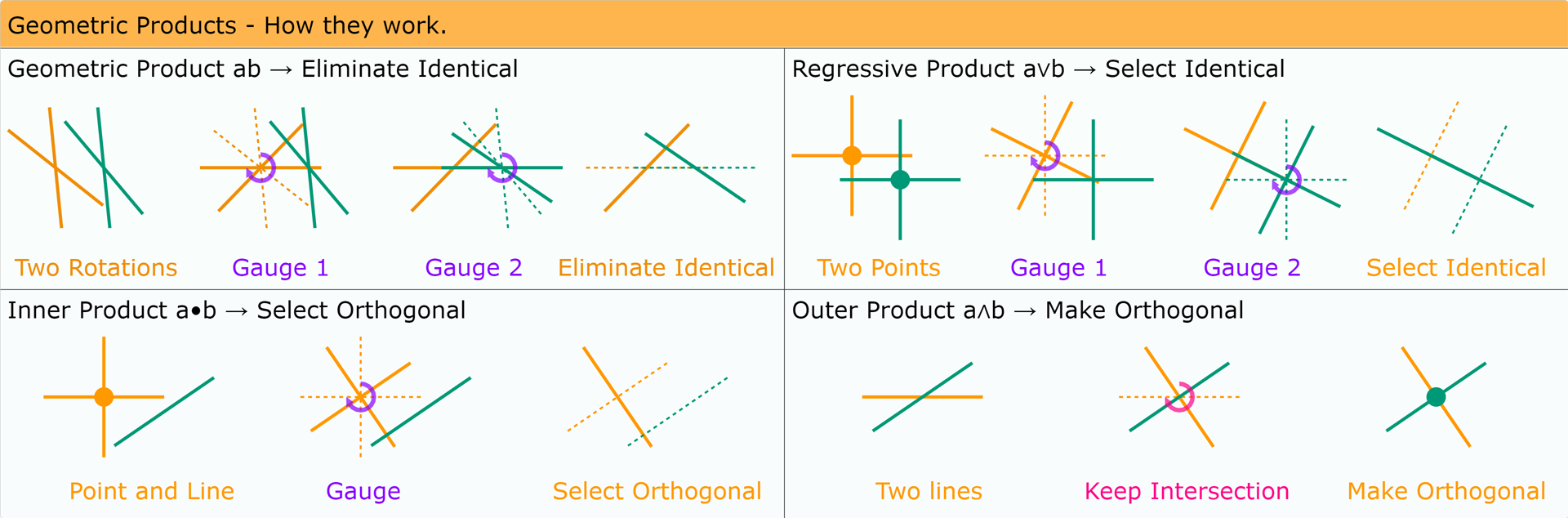
\(ab\) Geometric Product composes reflections
\(a\wedge b\) Outer Product Intersects elements
\(a\vee b\) Regressive Product joins elements
\(a\cdot b\) Dot Product rejects elements
Martin Roelfs
An Algebra for Geometry
{GA}

\((a\cdot b)b^{-1}\) projects \(a\) onto \(b\).
Martin Roelfs
An Algebra for Geometry
{GA}

Product of two bireflections
Martin Roelfs
An Algebra for Geometry
{GA}

Product of two bireflections
Martin Roelfs
An Algebra for Geometry
{GA}

The sandwich \(XYX^{-1}\) transforms the element \(Y\) with the element \(X\). Intuition:
Martin Roelfs
An Algebra for Geometry
{GA}
To rotate the red line \(l\) by \(ab\), we first rotate the space by \(ab\), then we combine with \(l\), and then we rotate the space back by \(ba\).
\(ab\) \(l\) \(ba\)

Reflection of the point \(bc\) in the line \(a\): \(a (bc) a\)
Martin Roelfs
An Algebra for Geometry
{GA}

\(ab\) Geometric Product composes reflections
Martin Roelfs
An Algebra for Geometry
{GA}

\(ab\) Geometric Product composes reflections
Martin Roelfs
An Algebra for Geometry
{GA}

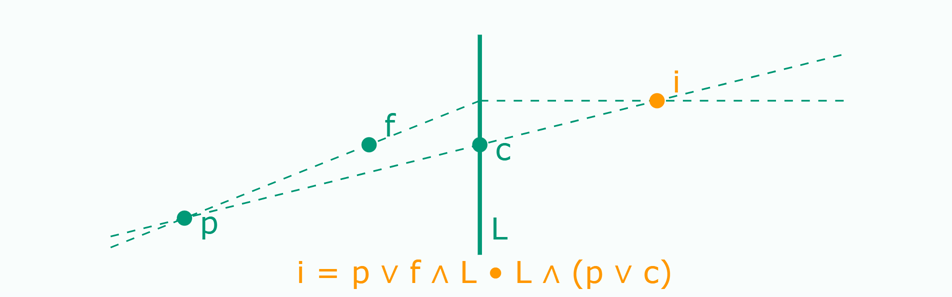
Formula can be read left to right, no information is hidden, no scalar ratios or coefficient calculations needed.
Martin Roelfs
An Algebra for Geometry
{GA}


- \( p \vee f \) = line through p and f
- \((p \vee f) \wedge L\) = intersection with lens
- \((p \vee f) \wedge L \cdot L \) = line orthogonal to L
- \(p \vee c \) = line through p and c
- \((p \vee f) \wedge L \cdot L \wedge (p \vee c)\) = intersect with line through center
\(\vee\) = join \(\wedge\) = meet \(\bullet\) = dot
Martin Roelfs
An Algebra for Geometry
{GA}

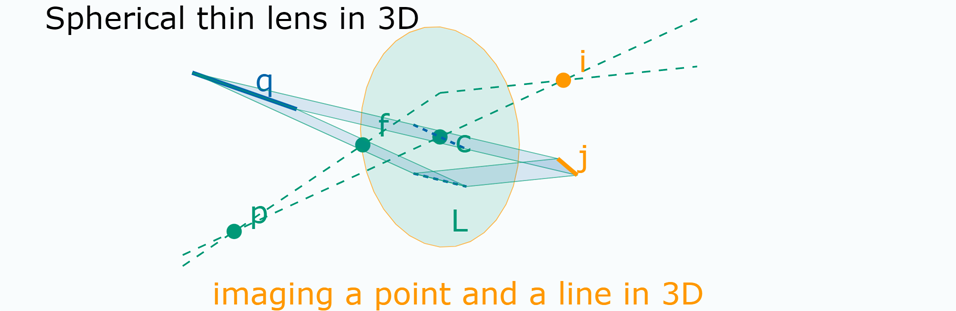
- Same formula in 3D!
- Same formula to calculate the image of a line! (just make \(p\) a line!)
Martin Roelfs
An Algebra for Geometry
{GA}

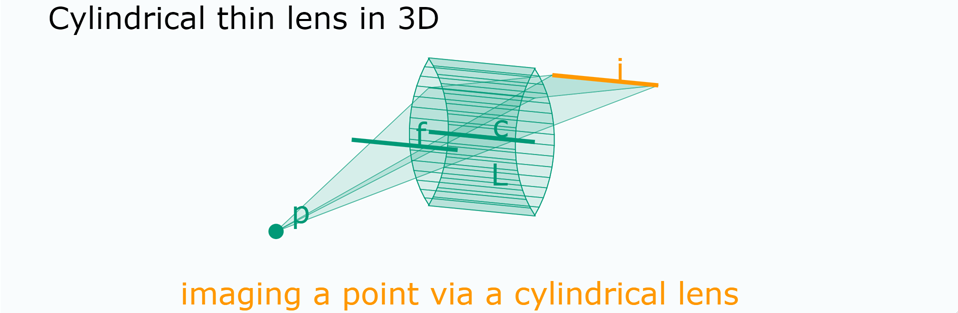
- Same formula for a cylindrical lens! (just make the focal and center a line!)
Martin Roelfs
An Algebra for Geometry
{GA}


\(d_i = \big ( \frac 1 f - \frac 1 {d_0} \big )^{-1}\qquad h_i=-\frac {d_i} {d_0} h_0\)
\(h_0 = (\overline{\vec c - \vec g} )\,\cdot\,(\vec c - \vec p) \)
\(d_0 = (\overline{\vec c - \vec f} )\,\cdot\,(\vec c - \vec p) \)
\(i = -d_i\overline{(\vec c - \vec f )} - h_i \overline{(\vec c - \vec g)} + \vec c \)
no need for :
- coordinates
- origin
- dimensionality
- arrows
- 'solving'
Martin Roelfs
An Algebra for Geometry
{GA}
{GA}
An Algebra for Geometry
Martin Roelfs

Key take aways
- The elements choose the dimensionality of the problem, not the space you represent it in. I.e. you could write down two points in a 17D space, but all their interactions are still 1D!
- All binary operators have this property.
- Geometric equations are dimension, origin, and signature independent. Pro tip: always try several dimensions, never stick to one.
{Part 2}
Implementing the Algebra of Geometry

All well and good, but how do I actually compute something?
Key observation: performing the same reflection twice is the same as doing nothing.
$$ vvXv^{-1}v^{-1} = v^2 X v^{-2} $$
I.e., \( v^2 = \pm 1 \).
Martin Roelfs
An Algebra for Geometry
{GA}
- In a Clifford (Geometric) Algebra, vectors square to scalars. I.e., for \( v \in \mathbb{R}_{p,q,r}, v^2 \in \mathbb{R} \)
- It is well-known that the products of vectors in a Clifford Algebra are elements of \( \text{Pin}(p,q,r) \).
Therefore our Algebra of Geometry can be represented using normalized vectors in a Clifford Algebra!


What on earth is the Clifford Algebra \( \mathbb{R}_{p,q,r}\)?
Martin Roelfs
An Algebra for Geometry
{GA}
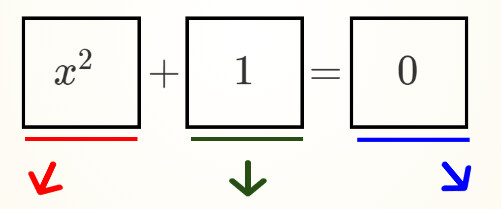
The Clifford Algebra \( \mathbb{R}_{p,q,r}\) has \(p\) positive, \(q\) negative, and \(r\) null basis vectors.

Consider the 2D example, \( \mathbb{R}_{2,0,0}\). This has basis vectors \(e_1, e_2\), satisfying \(e_1^2 = e_2^2 = 1\). Any vector is now of the form:
$$ u = a e_1 + b e_2. $$
Martin Roelfs
An Algebra for Geometry
{GA}
What is the square of \(u\)?
But there is nothing special about \(e_1\) and \(e_2\)! In fact, you might have chosen what I called \(u\) as one of your basis vectors. Therefore we must have
such that \( u^2 = a^2 + b^2 \). So orthogonal vectors anti-commute!

Any line is a linear combination \( u = ae_1 + be_2 \).
Martin Roelfs
An Algebra for Geometry
{GA}
We have also found a single point: \( e_{12} := e_1 e_2 \).

So we can now form lines through the origin \( e_{12} := e_1 e_2 \) as \(u = a e_1 + b e_2\). What is the square of the point \(e_{12}\)?
Martin Roelfs
An Algebra for Geometry
{GA}
We recognize the scalar part as the dot product \( u \cdot v = |u||v| \cos\theta \) of the two vectors, whereas the second part is the exterior product \( u \wedge v = |u||v| e_{12} \sin\theta \).
How about the product of two arbitrary lines through the origin?
It behaves like the imaginary unit \(i\)!
The product of two lines yields Euler's formula!

So we can now make all lines through the point \( e_{12}\), but we only have one point. We were promised origin independence! So where are the other points? To find them, we need another line orthogonal to \(e_1\) and \(e_2 \).
Martin Roelfs
An Algebra for Geometry
{GA}

Martin Roelfs
An Algebra for Geometry
{GA}
The line at infinity, \(e_0\), is orthogonal to \(e_1\) and \(e_2 \). Besides finding a new line, we also find two new points: \(e_{01}, e_{02}\). Because these lie at infinity, they are called directions.
Recall that lines are specified by the linear equation
$$ ax + by + \delta = 0 $$
We can thus represent arbitrary lines in 2D as
$$ u = ae_1 + be_2 + \delta e_0, $$
where \(\delta\) is the distance from the origin. Similarly, arbitrary directions (points on the horizon)
$$ p_\infty = y e_{01} + x e_{20} $$
whereas arbitrary points are given by
$$ p = e_{12} + p_\infty = e_{12} + y e_{01} + x e_{20} $$
What is the square of \(e_0\)? Well, you cannot reflect in the horizon and live to tell about it!

Martin Roelfs
An Algebra for Geometry
{GA}
Question: how would we now rotate around a given point \((x, y)\) by an angle \( \theta \)?
Since \(e_0^2 = 0\), all points are created equal:
$$ p^2 = e_{12}^2 = -1$$
Thus all points generate their own local Euler's formula under exponentiation:
$$ R = e^{\theta p} = \cos\theta + p \sin\theta$$
Directions are even easier, because they square to \(p_\infty^2 = 0\):
$$ R = e^{a p_\infty} = 1 + a p_\infty$$

Martin Roelfs
An Algebra for Geometry
{GA}
So we can straightforwardly rotate around any point \(X_0\) in space by sandwiching any quantity by \(R = e^{\theta p /2}\): \( X(\theta) = R X_0 R^{-1} = e^{\theta p /2} X_0 e^{-\theta p /2} \).

Martin Roelfs
An Algebra for Geometry
{GA}
Towards nD
In 2D we reflect in a line, in 3D in a plane, in nD in a hyperplane. In (pseudo-)Euclidean space \( E(p,q) \), hyperplanes satisfy the linear equation
$$ ax + by + cz + ... + \delta = 0 $$
Therefore, hyperplanes can be represented by vectors in \(\mathbb{R}_{p,q,1}\), with basis vectors \( \mathbf e_0^2= 0 \) and
\[ \mathbf e_1^2= \ldots = \mathbf e_p^2 = -\mathbf e_{p+1}^2= \ldots = -\mathbf e_{p+q}^2 = 1, \]
as
$$ v = a \mathbf e_1 + b\mathbf e_2 + c\mathbf e_3 + ... + \delta \mathbf e_0 $$
To reflect a hyperplane \(w\) in a hyperplane \(v\), use conjugation:
$$ w \to v[w] = v w v^{-1} $$

Martin Roelfs
An Algebra for Geometry
{GA}
The PGA for computer graphics: 3DPGA
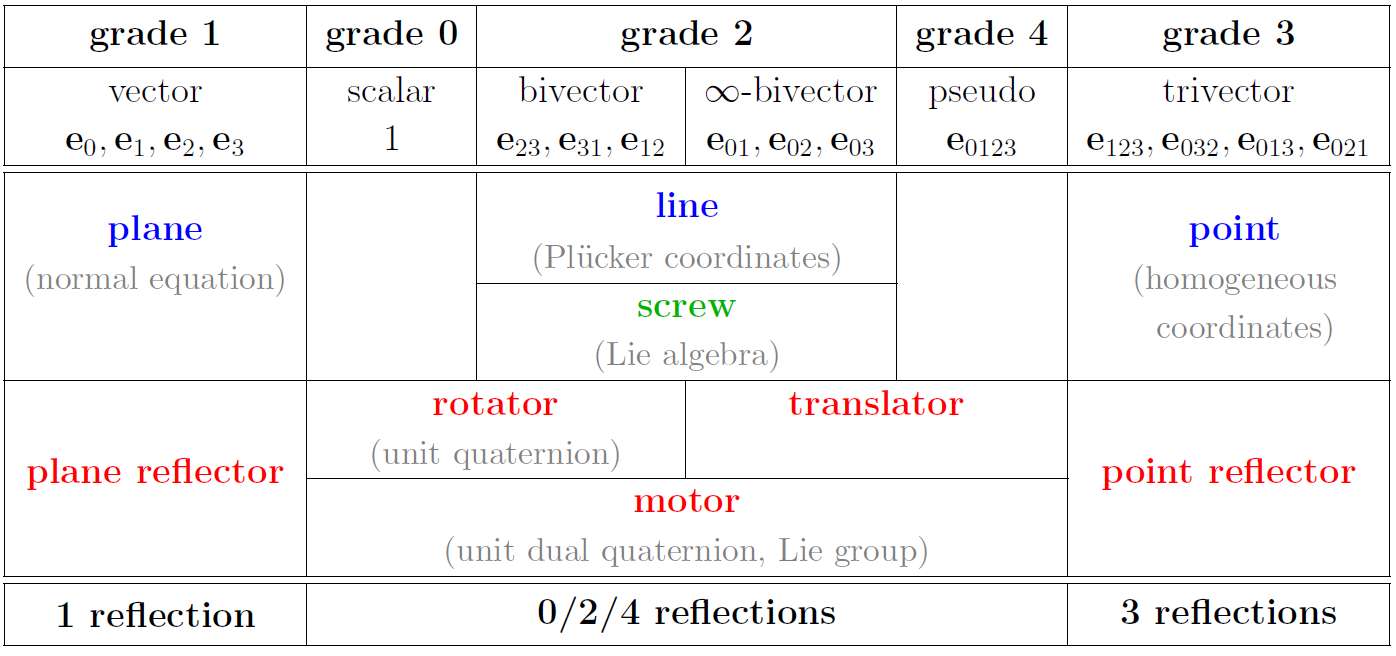
- PGA integrates objects and operators
- PGA relates all known computational representations
- PGA is real and understandable geometry
- PGA empowers the programmer
- PGA leads to very frugal, efficient code
- PGA is fun !

Martin Roelfs
An Algebra for Geometry
{GA}
Towards nD
Noteworthy spaces
| Describes | Algebra | Group | Name |
|---|---|---|---|
| 2D Plane | E(2) | "Planar quaternions" | |
| 3D Plane |
E(3) | Dual quaternions | |
| Spacetime* | SO(1,3) | Lorentz transformations | |
| Spacetime | Poin(3,1) | Poincare transformations |
Question: what is the difference between \(\mathbb{R}_{1,3,0}\) and \(\mathbb{R}_{1,3,1}\)?
{Part 3}
Closing remarks
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
scalar
vector
bivector
Martin Roelfs
An Algebra for Geometry
{GA}
Duality
Vectors are always \(d-1\) dimensional subspaces (hyperplanes). What if we want to make a true point, which remains a point if we change the dimension?
The dual of a \(d-k\) dimensional quantity is always a \(k\) dimensional quantity. E.g. in 2D, the dual of a line is a point. But in 3D, the dual of a plane, is also a point.
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
scalar
vector
bivector
Martin Roelfs
An Algebra for Geometry
{GA}
Duality
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
scalar
vector
bivector
Martin Roelfs
An Algebra for Geometry
{GA}
Forces + Torque = Forque
In the body frame :
push at origin = translation
push at infinity = rotation
Force and Torque are both lines.
in any # dimensions.
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
scalar
vector
bivector
Martin Roelfs
An Algebra for Geometry
{GA}
Forces + Torque = Forque
The forque line is the dual of the "axis" of the transformation.
- 2D: push along a line, around a point.
- 3D: push along a line, around a line.
- 3+1D: push along a line, around a plane.
- etc.
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
scalar
vector
bivector
Martin Roelfs
An Algebra for Geometry
{GA}
Closing statements
- PGA unifies all linear and angular phenomena:
- Translations and rotations
- Linear and angular momentum
- Force and Torque
- PGA allows us to write expressions that work in any number of dimensions
- As it should, because 2D is a subspace of 17D, so your expressions better work in both
- If an expression doesn't work across dimensions and signatures, it doesn't properly capture the geometry of the problem.
Thank you!
For more information, libs, tools and docs ...
https://bivector.net
Martin Roelfs
An Algebra for Geometry
{GA}
On to the ganja.js Coffeeshop!
{Part 4}
Visit to the ganja.js Coffeeshop!
{Part 2}
Beyond Cartan-Dieudonné: The Discovery of Invariant Geometry

What happens to points in the plane when we perform an increasing number of reflections?
Martin Roelfs
The Discovery of Invariant Geometry
{GA}

What happens to points in 3D space when we perform an increasing number of reflections?
Martin Roelfs
The Discovery of Invariant Geometry
{GA}

Clearly we found a new line, but which one is it? To answer this question we must use gauges.
Martin Roelfs
The Discovery of Invariant Geometry
{GA}
{Part 3}
The Geometry of Physics

One mans linear momentum is another mans angular momentum
Martin Roelfs
The Geometry of Physics
{GA}

One mans linear momentum is another mans angular momentum
Martin Roelfs
The Geometry of Physics
{GA}

One mans linear momentum is another mans angular momentum
Martin Roelfs
The Geometry of Physics
{GA}

Wigner rotation
Martin Roelfs
The Geometry of Physics
{GA}
Alice has velocity \( u_A \), while Bob has velocity \( u_B \). In order for Alice to see the world from Bob's perspective, she could simply reflect over the bisector
$$ \overline{u_A + u_B} = \frac{u_A + u_B}{\sqrt{2 + 2 u_A \cdot u_B}} $$
However, this would leave her PT inverted, which may or may not be fatal, so it's best to first perform an extra reflection in place just to be sure:
$$ \Lambda = (\overline{u_A + u_B}) u_A^{-1} $$
This is the boost to transform from Alice to Bob:
$$ \Lambda u_A \widetilde{\Lambda} = u_B$$
{An Algebra for Geometry}
Part 1: Theory and motivation

Introduction to Geometric Algebra in just 15 mins.
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
+
+
scalar
vector
bivector
- Start from purely geometric reasoning.
- Find if there is a known mathematical structure onto which this maps.
Martin Roelfs
An Algebra for Geometry
{GA}
The atoms of Geometry turn out to be reflections

Martin Roelfs
An Algebra for Geometry
{GA}

Thank you!
For more information, libs, tools and docs ...
https://bivector.net
Martin Roelfs
An Algebra for Geometry
{GA}
{An Algebra for Geometry}
Part 2: Refresher and Hands on
Hands-on session on Geometric algebra
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
+
+
scalar
vector
bivector
- In the previous session we learned that the atoms of geometry are reflections
- Reflections and elements of geometry are in a one-to-one correspondence. E.g. plane(-reflections), line(-reflections), point(-reflections).
Martin Roelfs
An Algebra for Geometry
{GA}
- We will see how to construct planes, lines and points in 3D
- Examples
Answer to some questions
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
+
+
scalar
vector
bivector
- Theofanis: why it is worth knowing PGA if your (CAD) software already has functions for everything.
Martin Roelfs
An Algebra for Geometry
{GA}
// construct lines
line_from_points (p1, p2)
line_from_points_and_dir (p, d)
line_from_plucker (a, b, c, d, e, f)
// construct planes
plane_from_points (p1, p2, p3)
plane_from_point_and_dirs (p, d1, d2)
plane_from_points_and_dir (p1, p2, d)
plane_from_point_and_line (p, l)
plane_from_equation (a, b, c, d)
// Intersections
intersect_line_plane (l, P)
intersect_plane_plane (P1, P2)
intersect_planes (P1, P2, P3)
// Projections
project_point_plane (p, P)
project_line_plane (l, P)
project_point_line (p, l)// construct transformations
mtx_translate (x, y, z)
mtx_rotate_euler (h, p, b)
mtx_rotate_axis_angle (x, y, z, a)
mtx_look_at (from, too, pole)
// apply transformations
transform_point (M, p)
transform_direction (M, d)
transform_line (M, l)
transform_plane (M, P)
Answer: if you call a couple of such functions in a sequence, there is no way to see if this can be simplified. If all of these operations are algebraic expressions on the other hand, you can simplify them.
- Alexander: can we do extrusions? Example will follow later.
- Peter: how does this compare to matrices? Answer: I'll have a slide on this in a moment.

- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
scalar
vector
bivector
Martin Roelfs
An Algebra for Geometry
{GA}
In 2D we reflect in a line, in 3D in a plane, in nD in a hyperplane. In (pseudo-)Euclidean space \( E(p,q) \), hyperplanes satisfy the linear equation
$$ ax + by + cz + ... + \delta = 0 $$
Therefore, hyperplanes can be represented by vectors in \(\mathbb{R}_{p,q,1}\), with basis vectors \( \mathbf e_0^2= 0 \) and
\[ \mathbf e_1^2= \ldots = \mathbf e_p^2 = -\mathbf e_{p+1}^2= \ldots = -\mathbf e_{p+q}^2 = 1, \]
as
$$ v = a \mathbf e_1 + b\mathbf e_2 + c\mathbf e_3 + ... + \delta \mathbf e_0 $$
To reflect a hyperplane \(w\) in a hyperplane \(v\), use conjugation:
$$ w \to v[w] = - v w v^{-1} $$
Reflections are involutory, and thus demanding
$$ v[v[w]] = w $$
leads to \( v^2 = v^{-2} = \pm 1 \).
Importantly, \( v[v] = -v \).
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
scalar
vector
bivector
Martin Roelfs
An Algebra for Geometry
{GA}
In \(d\) dimensions, we start from reflections in \( d-1 \) dimensional hyperplanes. \(k\) of these can then be intersected to form \( d - k \) dimensional elements of geometry.
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
scalar
vector
bivector
Martin Roelfs
An Algebra for Geometry
{GA}
The composition of two reflections leads to a handedness preserving isometry.
We call such transformations
Bireflections
Bireflections \( R = uv \) preserve handedness, and are continuous transformations.
Why two-sided transformations? If I ask you to write upside down, what is the easiest way to do it?

Comparison to matrices
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
+
+
scalar
vector
bivector
Martin Roelfs
An Algebra for Geometry
{GA}
In order to transform a point by a rotation and a translation in linear algebra, e.g. open3d.geometry.PointCloud.transform, we use the covariant transformation
where \( \vec{p}_\infty \) is a 3-vector indicating a point on the horizon, \(p_o \) is the origin, \(R\) is a 3x3 rotation matrix, and \(t\) is a 3-vector encoding the translation.
This 4x4 matrix uses 16 floats, and can only transform points. For planes we have to use the 4x4 contravariant rep., and for lines the 6x6 adjoint rep. By contrast, the PGA equivalent rotor
$$ R = a + b\mathbf{e}_{23} + c\mathbf{e}_{31} + d\mathbf{e}_{12} + e\mathbf{e}_{01} + f\mathbf{e}_{02} + g\mathbf{e}_{03} + h\mathbf{e}_{0123} $$
transforms points, lines and planes identically using only 8 floats.

- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
+
+
scalar
vector
bivector
Martin Roelfs
An Algebra for Geometry
{GA}
What about performance ?
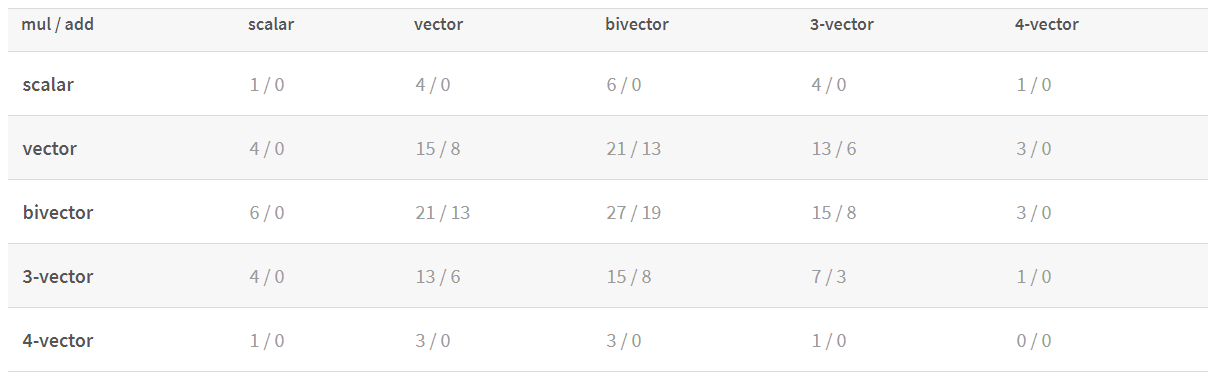
4x4 matrix multiplication : 64 multiplications, 48 additions, 16 floats
PGA motor multiplication : 48 multiplications, 40 additions, 8 floats
with a similar picture for the other elements :
- not just a new way to shuffle coordinates.
- not just the quotient of the tensor algebra with some ideal.
- not just the extension of vector algebra to multivectors.
scalar
vector
bivector
Martin Roelfs
An Algebra for Geometry
{GA}
As

Martin Roelfs
An Algebra for Geometry