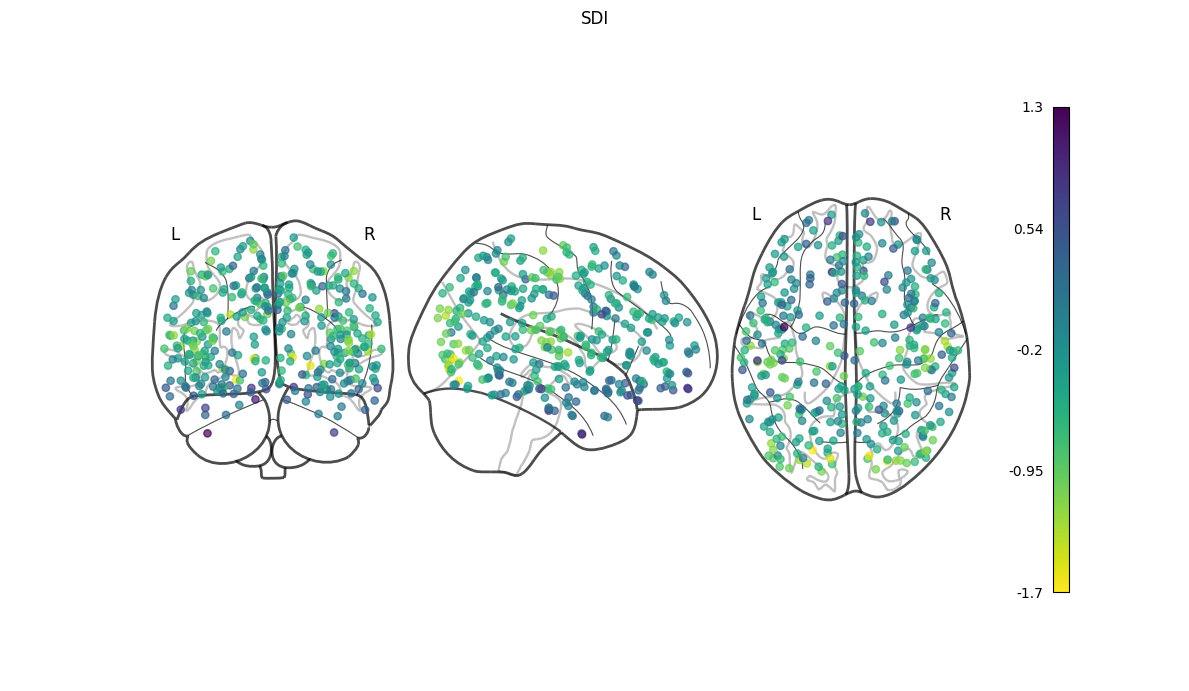
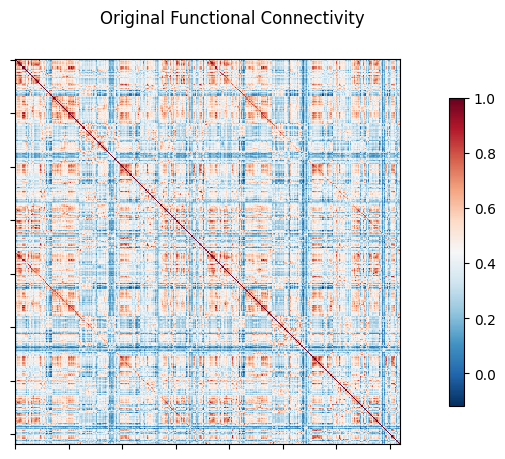
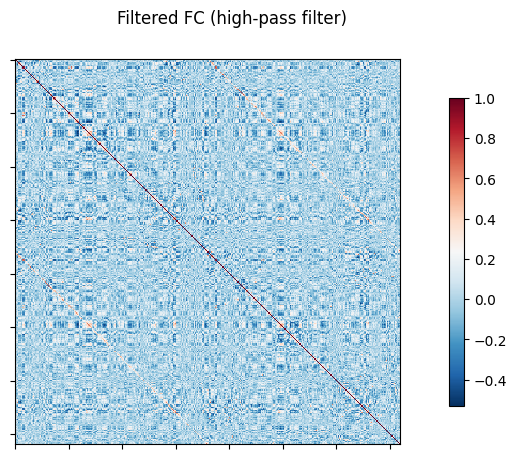
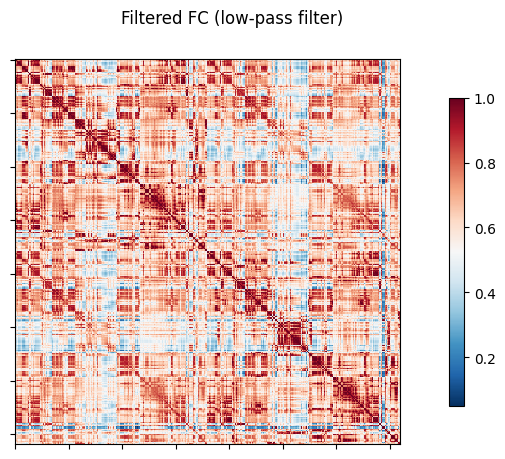
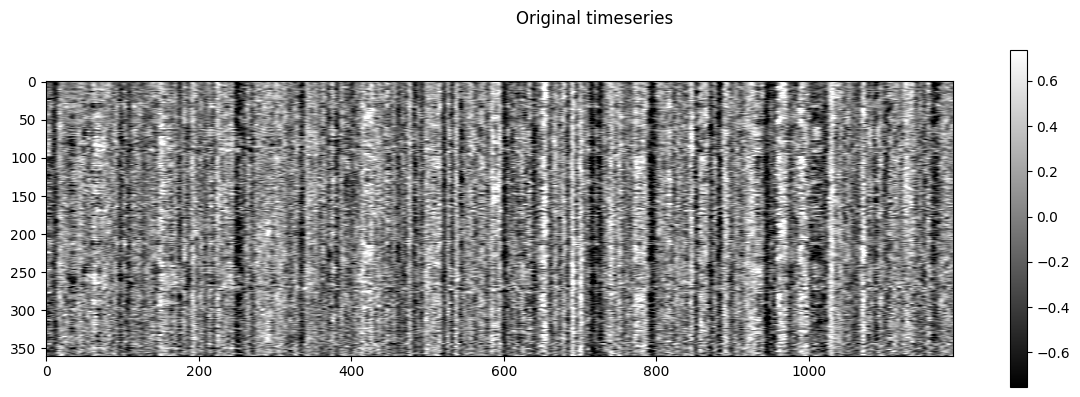
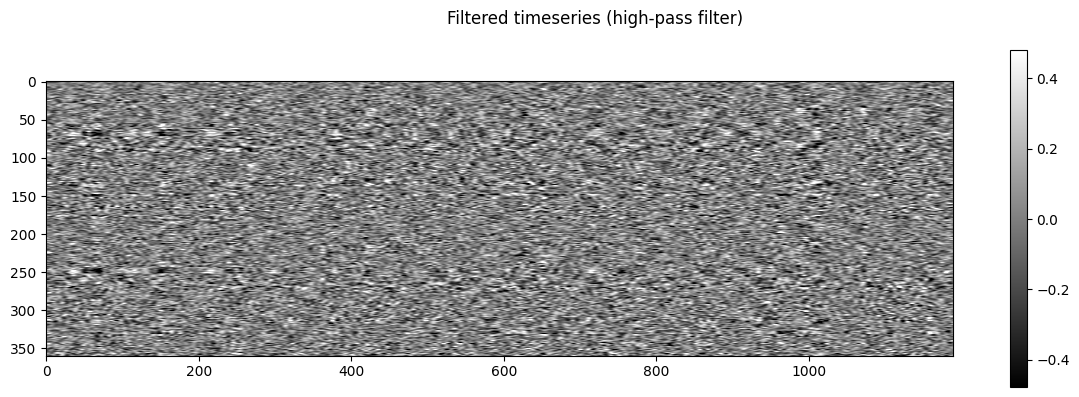
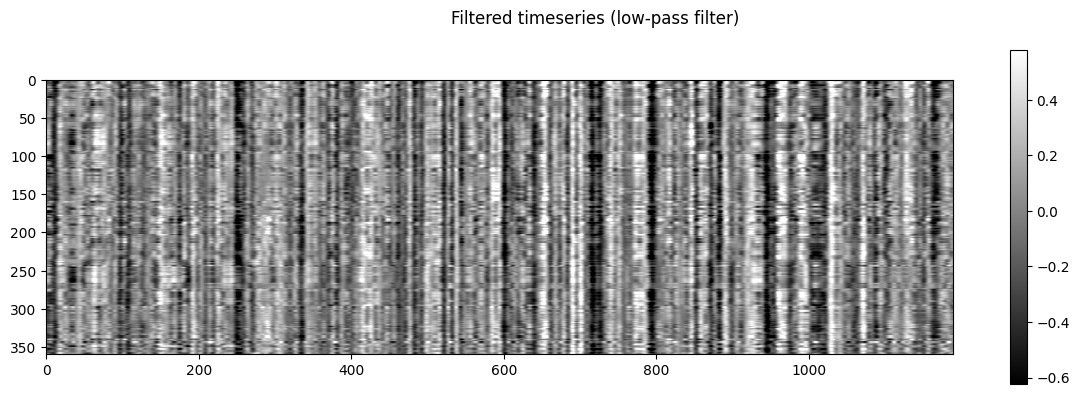
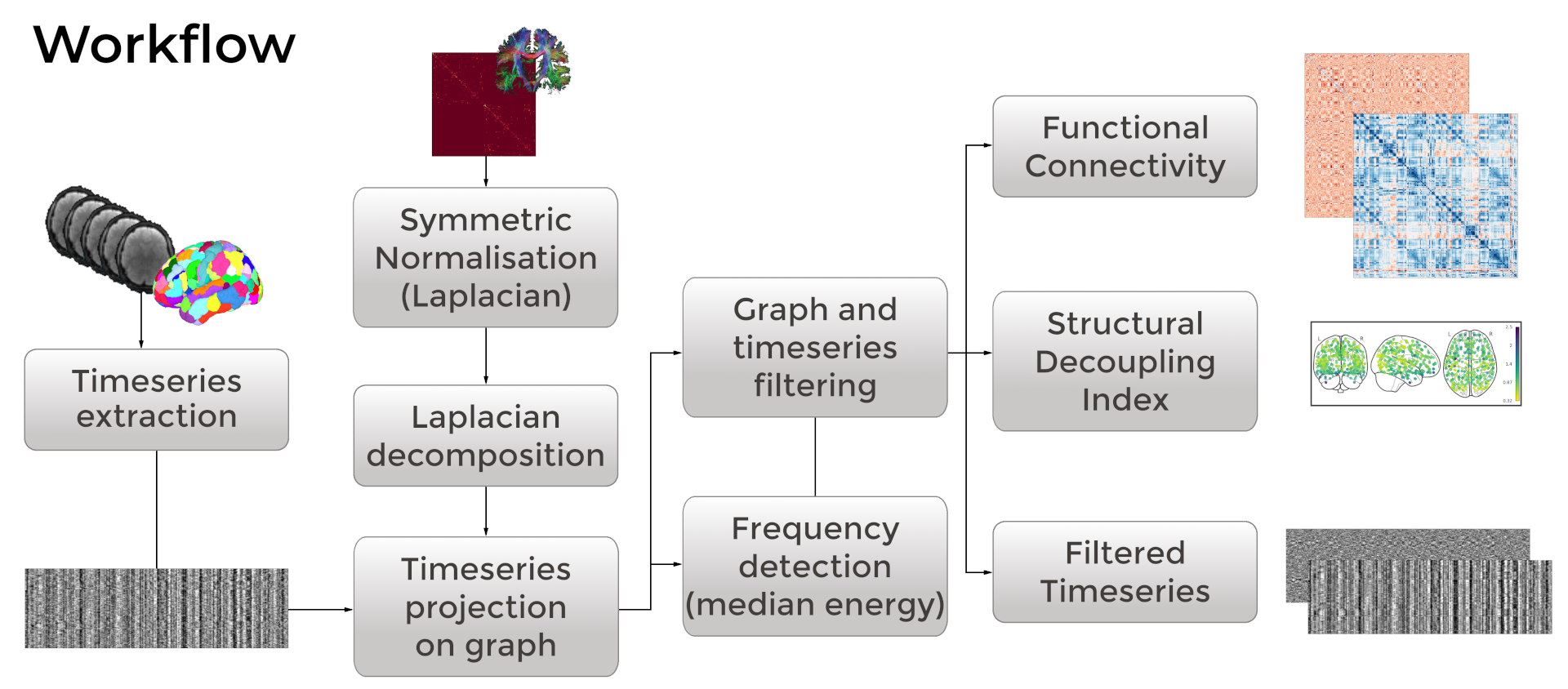
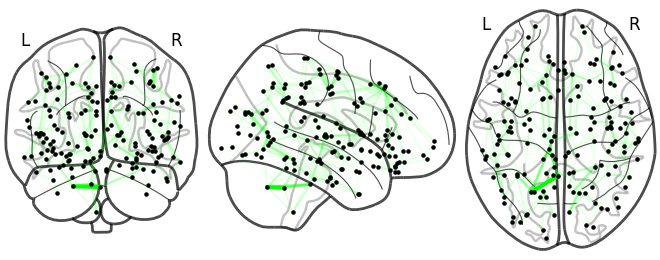
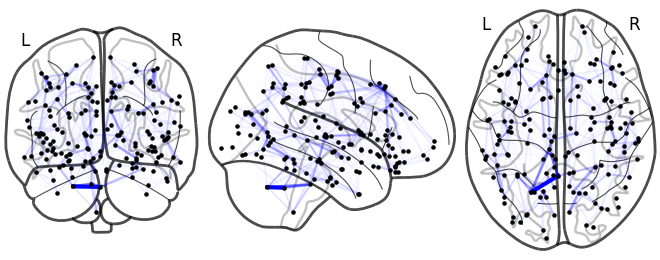
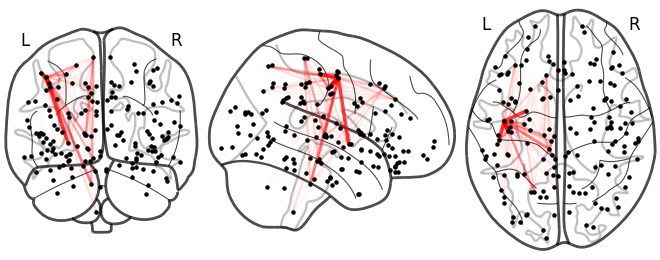
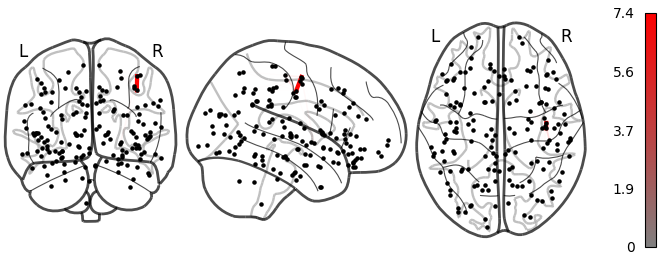
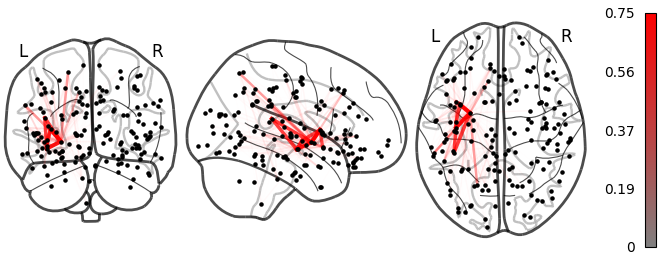
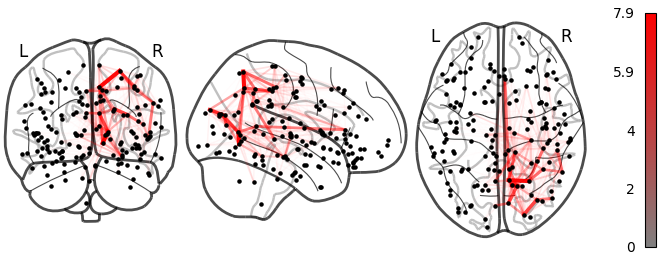
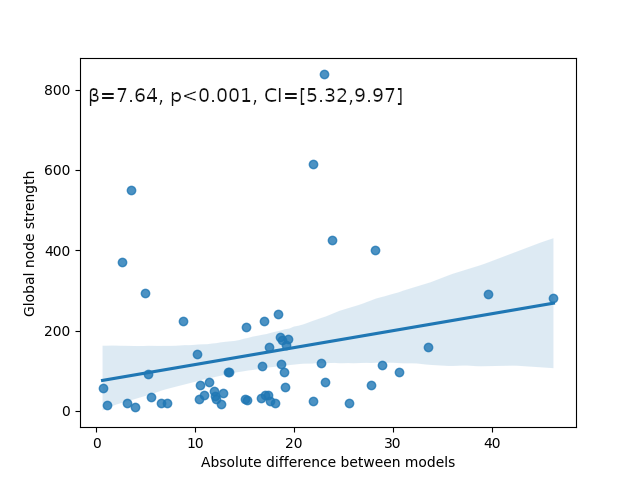
NiGPS: Graph Signal Processing
on Multimodal MRI data.

Stefano Moia¹ ², Julia Brugger¹ ³, Philip Egger¹ ³, Giorgia Giulia Evangelista¹ ³, Friedhelm Cristoph Hummel¹ ³ ⁴, Maria Giulia Preti¹ ², and Dimitri Van De Ville¹ ²

1. Neuro-X Institute, École polytechnique fédérale de Lausanne, Geneva, Switzerland    2. Department of Radiology and Medical Informatics (DRIM), Faculty of Medicine, University of Geneva, Geneva, Switzerland    3. Neuro-X Institute, EPFL Valais, Clinique Romande de Réadaptation, Sion, Switzerland    4. Department of Clinical Neurosciences, Geneva University Hospital (HUG), Geneva, Switzerland

smoia
@SteMoia
s.moia.research@gmail.com
Stefano Moia, 2023

I have no financial interests or relationships to disclose with regard to the subject matter of this presentation.

Speaker name: Stefano Moia

Declaration of Financial Interests or Relationships

Graph Signal Processing: brain applications

  • Novel approach to signal processing, based on graph embedding of timeseries¹.
  • Useful for multimodal brain imaging².
  • GSP applications can improve subject identification³, improve data smoothing⁴, and reveal structural/functional coupling patterns agreeing with cognitive domain hierarchy and genetic expression⁵.

1. Ortega (2022) Introduction to Graph signal Processing,
3. Griffa et al. (2022) Neuroimage,
5. Preti, Van De Ville (2019) Nat. Commun.

2. Huang et al. (2018) Proc. IEEE,
4. Abramian (2021) Neuroimage,

Shuman et al. (2013) IEEE Signal Process Mag

Huang et al. (2018) Proc. IEEE

Huang et al. (2018) Proc. IEEE

NiGSP

NiGSP is an open development python based module to apply
Graph Signal Processing, with emphasis on neuroimaging applications (atlas based)

It offers a set of function for filter creations, filtering, visualisation,
and metrics computations

NiGSP: workflow

nigsp -f timeseries.nii.gz -s sc_mtx.tsv -a atlas.nii.gz --informed-surrogates -n 1000

Based on Preti, Van De Ville (2019) Nat. Commun. and Griffa et al. (2022) Neuroimage

Sneak peak: GSP-based diffusivity model

\Delta Y = (- \tau_1 \mathcal{L}_1 - \tau_2 \mathcal{L}_2) Y + E \quad \leftrightarrow \quad E_n = \Delta Y + ( \tau_1 \mathcal{L}_1 + \tau_2 \mathcal{L}_2) Y_{n-1}
\Delta Y = -\tau \mathcal{L} Y + E \quad \leftrightarrow \quad E_n = \Delta Y + \tau \mathcal{L} Y_{n-1}

Total

Unaffected

Affected

Sneak peak: GSP-based diffusivity model

Small

Medium

Large

Lesion global node strength

One vs two laplacian(s) model, difference of absolute estimated timeseries

That's all folks!

Thanks to...

...the MIP:Lab @ EPFL

...you for the (sustained) attention!

Stefano Moia, 2023

NiGPS: Graph Signal Processing on Multimodal MRI data (ISMRM 2023)

By Stefano Moia

NiGPS: Graph Signal Processing on Multimodal MRI data (ISMRM 2023)

CC-BY 4.0 Stefano Moia, 2023. Images are property of the original authors and should be shared following their respective licences. This presentation is otherwise licensed under CC BY 4.0. To view a copy of this license, visit https://creativecommons.org/licenses/by/4.0/

  • 108

More from Stefano Moia