An exponential-free structure preserving integrator for stochastic Lie–Poisson systems

Erik Jansson

Joint work with:

 

  • Annika Lang (Chalmers/University of Gothenburg)
  • Sagy Ephrati (Chalmers/University of Gothenburg)
  • Erwin Luesink (University of Amsterdam )

Made possible by:

 

  1. Klas Modin and Milo Viviani. Lie–Poisson methods for isospectral flows. Foundations of Computational
    Mathematics    , 20:889–921, 2020.

  2. Grigori N. Milstein and Michael V. Tretyakov. Stochastic Numerics for Mathematical Physics. Springer
    Berlin Heidelberg, 2004.
  3. Charles-Edouard Bréhier, David Cohen, and Tobias Jahnke. Splitting integrators for stochastic Lie–
    Poisson systems. Mathematics of Computation, 92(343):2167–2216, 2023.

Talk based on:

asdasdasd

 

 

arxiv:2408.16701

Overview

  • Which systems?
  • How to make them stochastic?
  • The need for structure-preserving integration
  • How to derive the integrator?
  • How to prove that it does what it should?

Examples of systems

Stochastic rigid body

Stochastic (sine) Euler equations

Stochastic point vortex dynamics

Lie-Poisson systems

Lie group \(G\) with algebra \(\mathfrak{g}\)

Hamiltonian \(H\colon \mathfrak{g}^* \to \mathbb R\)

\,\dot X_t = \operatorname{ad}^*_{\nabla H(X_t)} X_t\,
\langle \operatorname{ad}_U^*X,V \rangle = \langle X,[U,V] \rangle

Two ingredients

Lie-Poisson systems

Important geometric structure:

LP Systems evolve on coadjoint orbits

(symplectic manifolds that foliate space!)

+ Several preserved quantities, Hamiltonian, Casimirs etc.

\mathcal{O}_{X} = \{g^* X (g^*)^{-1}\colon g \in G\}

Coadjoint orbits

Dynamics on orbit

Lie-Poisson systems

+ Several preserved quantities, Hamiltonian, Casimirs etc.

\mathcal{O}_{X} = \{g^* X (g^*)^{-1}\colon g \in G\}

rigid body, spin systems: concentric spheres

Important geometric structure:

LP Systems evolve on coadjoint orbits

(symplectic manifolds that foliate space!)

Lie-Poisson systems

\(G \subset \operatorname{GL}(n)\) is compact, simply connected and \(J\)-quadratic, i.e., \(A \in \mathfrak{g} \iff AJ + JA^* = 0 \)

Examples: \(\mathfrak{so}(N), \mathfrak{su}(N), \mathfrak{sp}(N)\).

In this setting, LP flow is isospectral:

\, \dot X_t = [\nabla H(X_t)^*, X_t] \,

Examples of LP systems

Classic example: rigid body (ODE)

  • Algebra: \(\mathfrak{so}(3) \cong \mathbb R^3\)
  • Bracket: \([v,w] = w \times v\)
  • Hamiltonian: \(H(v) = v \cdot Iv\)

Examples of LP systems

Spin systems and point vortex dynamics:

  • Algebra: \(\mathfrak{su}(2)^N \cong (\mathbb R^{3})^N\)
  • Bracket: \([X_i,X_j] = X_i \times X_j \)
  • Hamiltonian: \(H(X_1, \ldots, X_n) {=} -\frac{1}{4\pi} \sum_{j=1}^n \sum_{i=1}^{j-1} \Gamma_{ij} \log\left(1{-} \frac{\operatorname{Tr}(X_i^* X_j)}{\|X_i \|^2 \|X_j \|^2}\right) \)

Examples of LP systems

Spherical Zeitlin-Euler equations (Sine-Euler)

  • Algebra: Skew-Hermitian matrices \(\mathfrak{su}(N)\)
  • Bracket: Matrix commutator \([\cdot,\cdot]\)
  • Hamiltonian: \(H(W) = -\frac{1}{2}\operatorname{Tr}( (\Delta_N^{-1}W)^*W)\)
\dot W = -[\Delta_N W, W]

Introducing stochasticisty

How to add noise to equations?

  • \(M\) independent scalar Brownian motions \(W^1, \ldots, W^M\)
  • \(M\) noise Hamiltonians \(H_k\colon\mathfrak{g}^*\to \R\)
~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~ 

Introducing stochasticisty

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~ 

Why Strato?

Why these coefficients?

We need a chain rule

Same bracket-type coefficient: same geometric structure

Stochastic LP Systems evolve on coadjoint orbits and have Casimirs!

Introducing stochasticisty

Stochastic LP Systems evolve on coadjoint orbits and have Casimirs!

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~ 

Coadjoint orbits

With transport noise

With non-transport noise

Geometric structure is needed

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~ 

What to assume to prove the existence of solutions?

E.g. Lipschitz is not realistic to assume

But! Some smoothness is sufficient for global existence

System remains on compact level sets of Casimirs
\(\rightarrow\) truncation argument to prove existence

Example of stochastic LP system

Zeitlin-Euler equations (Sine-Euler)

Know as SALT (Model unresolvable dynamics as stochastic forcing)

  • Algebra: Skew-Hermitian matrices \(\mathfrak{su}(N)\)
  • Bracket: Matrix commutator \([\cdot,\cdot]\)
  • Deterministic Hamiltonian: \(H_0(W) = -\frac{1}{2}\operatorname{Tr}( (\Delta_N^{-1}W)^*W)\)
  • Stochastic Hamiltonians: \(H_k =  ?\)
~ \mathrm d X_t =[\Delta_N^{-1} X_t ,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~ 

Example of stochastic LP system

  • Transport noise \(\rightarrow\) Move to Itô formulation
  • Correction is a dissipative term
  • Clever choice of coefficients + limit

= Navier–Stokes like behavior!

"Regularization by noise"

Careful results by Flandoli et al. in case of the flat torus for "real" Euler equations

Todo: Check the spherical case and check behavior in Zeitlin–Euler case

Structure preservation -

for accurate numerics

Classic example: rigid body

  • Algebra: \(\mathfrak{so}(3) \cong \mathbb R^3\)
  • Bracket: \([v,w] = w \times v\)

Structure preservation -

for accurate numerics

What happens if we apply an off the shelf integrator?

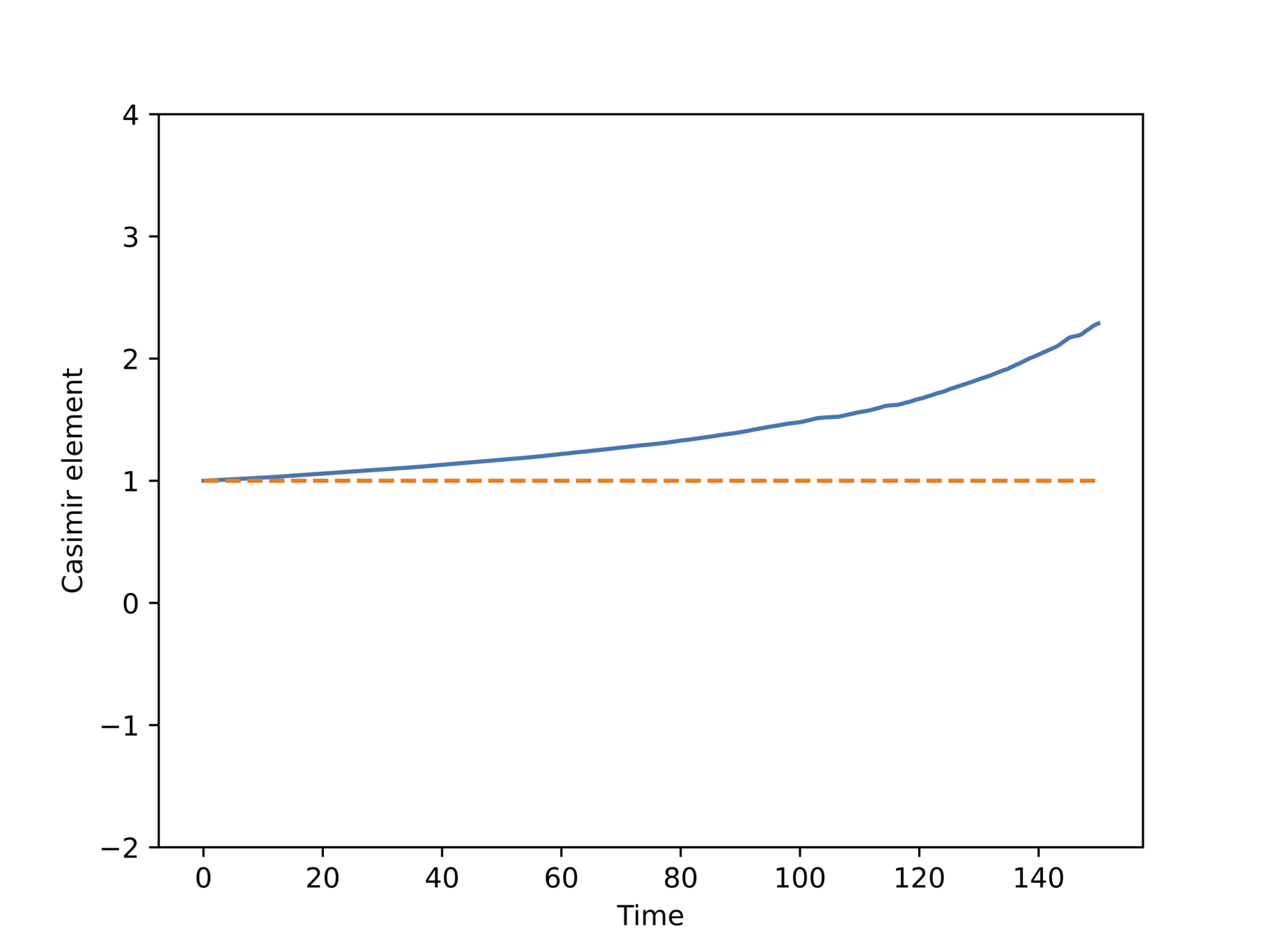
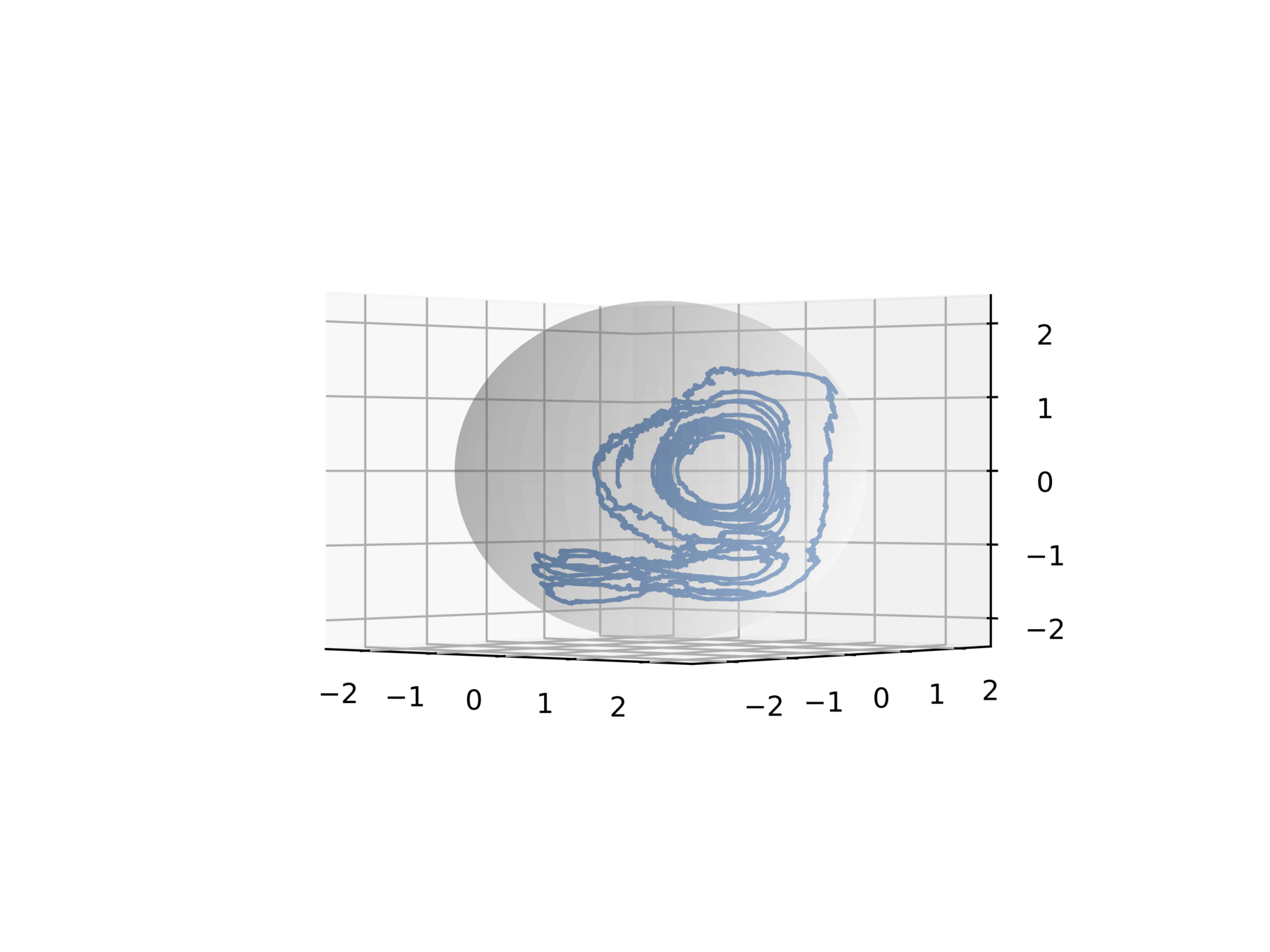
Non-physical behavior!

Structure preservation -

for accurate numerics

What happens with structure-preserving integrators?

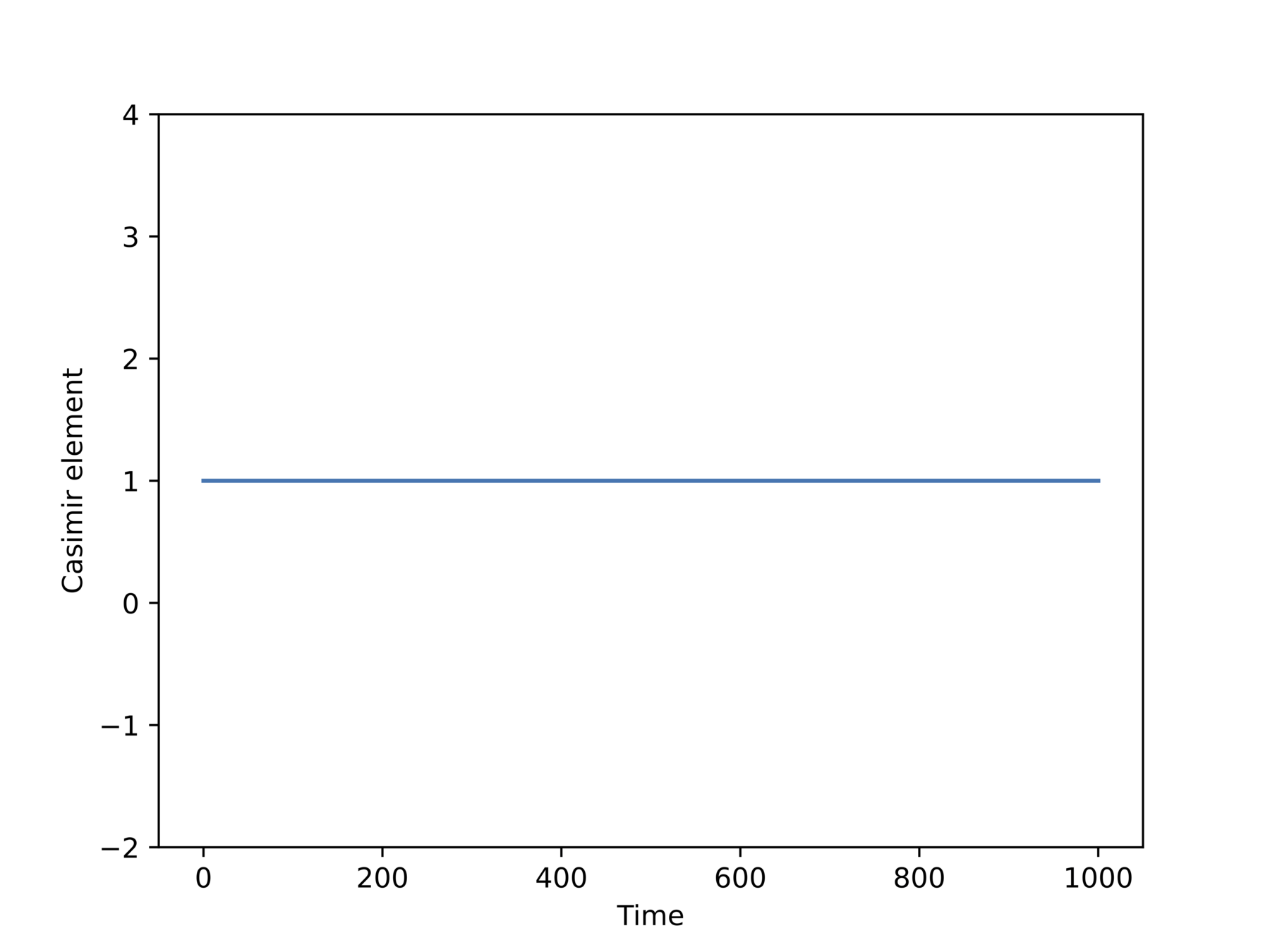
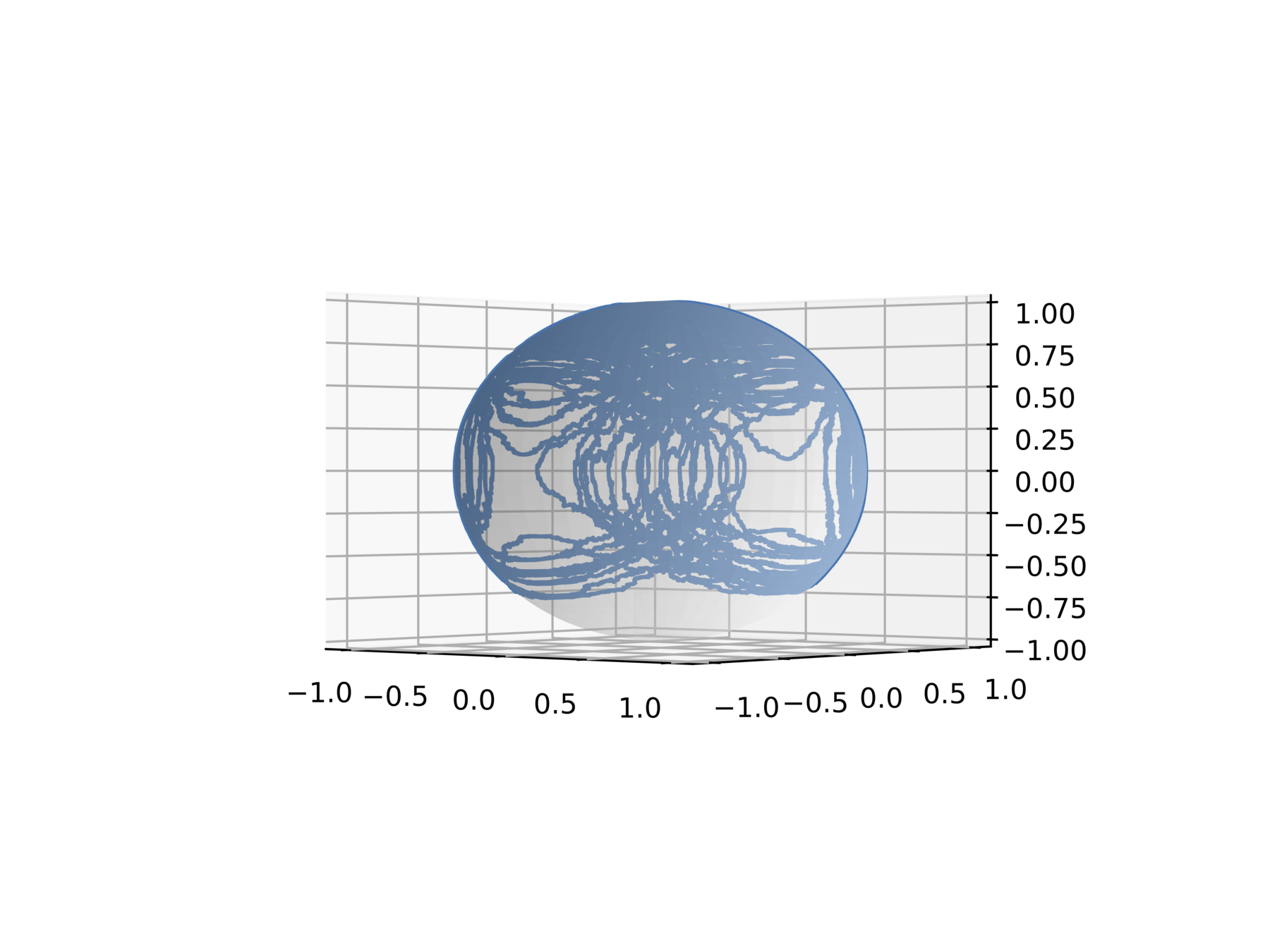
Structure preservation -

for accurate numerics

Wish list:

  • Preserve Casimirs a.s.
  • Preserve symplectic structure on coadjoint orbits a.s.

= Lie–Poisson integrator

Also: Avoid exponential map! (expensive, matrices in our applications are \(\sim2000\times2000\) )

Unreducing LP systems

LP systems on \(\mathfrak{g}^*\) are reductions of Hamiltonian systems on \(T^*G \cong G \times \mathfrak{g}^*\)

\(H\colon \mathfrak{g}^* \to \mathbb R\) lifts to left-invariant Hamiltonian!

\(G\) acts on \(T^*G\) by \(g.(Q,P) = (gQ,g^{-*}P)\)

Associated momentum map:

\mu(Q,P) = \frac{1}{2} Q^* P -\frac{1}{2c}J P^* Q J \in \mathfrak{g}^*
\tilde{H}(Q,P) = H(\mu(Q,P))

Unreducing LP systems

Do for all Hamiltonians!

\begin{split} \mathrm d Q_t &= Q_t\nabla H_0(\mu(Q_t,P_t)) \, \mathrm d t + \sum_{i=1}^M Q_t \nabla H_i (\mu(Q_t,P_t))\circ \mathrm d W_t^i, \\ \mathrm d P_t &= -P_t\nabla H_0(\mu(Q_t,P_t))^* \, \mathrm d t - \sum_{i=1}^M P_t \nabla H_i (\mu(Q_t,P_t))^* \circ \mathrm d W_t^i. \end{split}

Note: No a priori guarantee that this system remains on \(T^*G\)!

Embedded into \((R^{n \times n})^2\)

However! Remains on \(T^*G\)

Unreducing LP systems

\begin{split} \mathrm d Q_t &= Q_t\nabla H_0(\mu(Q_t,P_t)) \, \mathrm d t + \sum_{i=1}^M Q_t \nabla H_i (\mu(Q_t,P_t))\circ \mathrm d W_t^i, \\ \mathrm d P_t &= -P_t\nabla H_0(\mu(Q_t,P_t))^* \, \mathrm d t - \sum_{i=1}^M P_t \nabla H_i (\mu(Q_t,P_t))^* \circ \mathrm d W_t^i. \end{split}

Existence and uniqueness: follows by truncation argument (system remains on \(G \times \mathcal{O}_{\mu(Q_0,P_0)})\)

Unreducing LP systems

\begin{split} \mathrm d Q_t &= Q_t\nabla H_0(\mu(Q_t,P_t)) \, \mathrm d t + \sum_{i=1}^M Q_t \nabla H_i (\mu(Q_t,P_t))\circ \mathrm d W_t^i, \\ \mathrm d P_t &= -P_t\nabla H_0(\mu(Q_t,P_t))^* \, \mathrm d t - \sum_{i=1}^M P_t \nabla H_i (\mu(Q_t,P_t))^* \circ \mathrm d W_t^i. \end{split}

\(X_t = \mu(Q_t,P_t) \in \mathfrak{g}^*\) satisfies

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~ 

\(\Phi_h \colon T^*G \to T^* G\): \(G\)-equivariant symplectic integrator \(\rightarrow\)
Reduces to a Lie–Poisson integrator by \(\mu\)

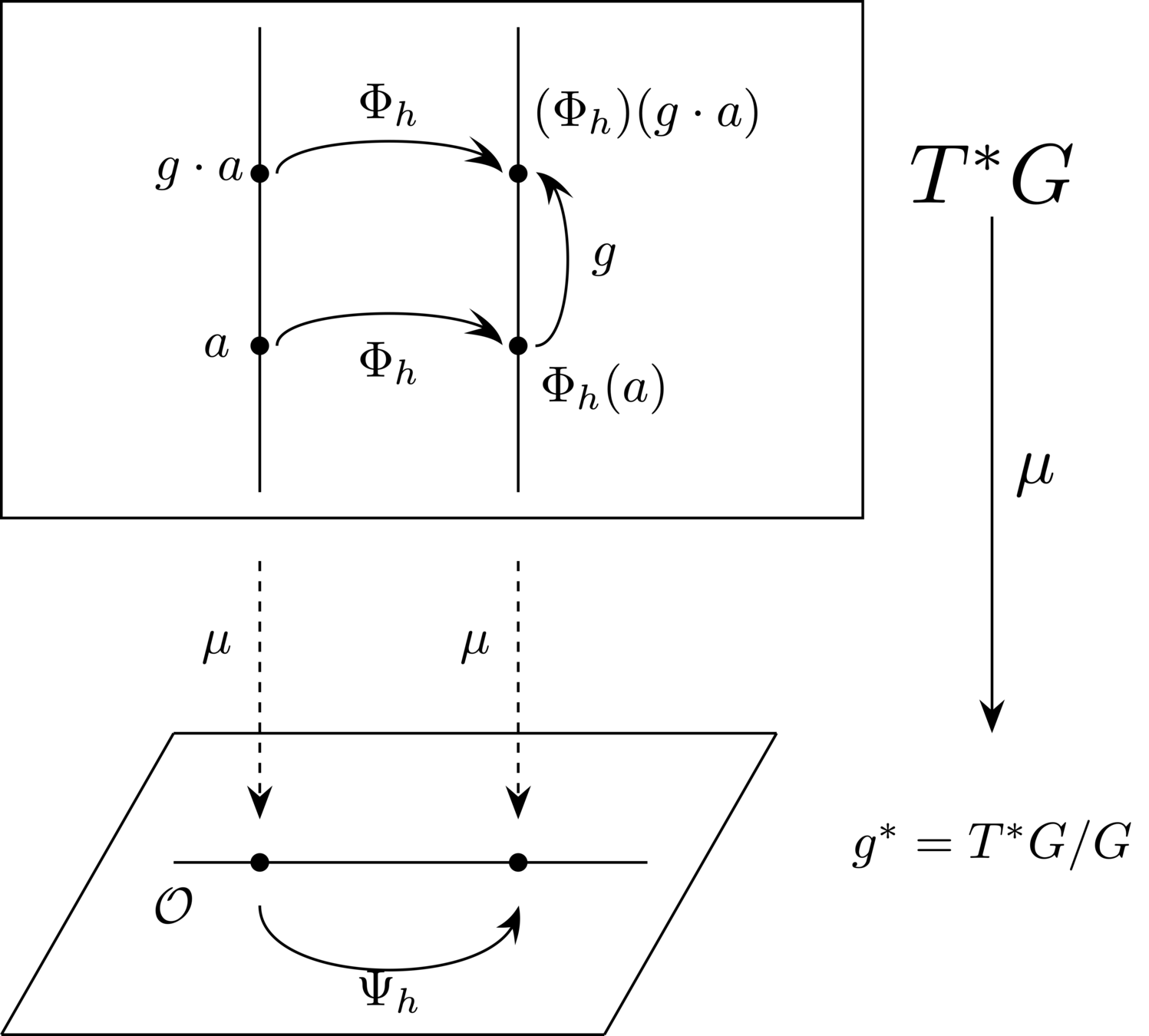
Integration without tears

Exploit the unreduction!

\begin{split} \mathrm d Q_t &= Q_t\nabla H_0(\mu(Q_t,P_t)) \, \mathrm d t + \sum_{i=1}^M Q_t \nabla H_i (\mu(Q_t,P_t))\circ \mathrm d W_t^i, \\ \mathrm d P_t &= -P_t\nabla H_0(\mu(Q_t,P_t))^* \, \mathrm d t - \sum_{i=1}^M P_t \nabla H_i (\mu(Q_t,P_t))^* \circ \mathrm d W_t^i. \end{split}
~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~ 

Integration without tears

Do we know such an integrator?

Implicit midpoint!

\begin{split} \Phi_h^{(1)} &\colon \begin{cases} Q_n & = \tilde{Q}- \frac{1}{2}\left( f_0(\tilde{Q}, \tilde{P}) h + \sum_{i=1}^M f_i(\tilde{Q}, \tilde{P})(\zeta_{i})_n \sqrt{h}\right), \\ P_n & = \tilde{P}-\frac{1}{2}\left(k_0(\tilde{Q}, \tilde{P}) h + \sum_{i=1}^M k_i(\tilde{Q}, \tilde{P})(\zeta_{i})_n\sqrt{h} \right), \end{cases} \\ \Phi_h^{(2)} &\colon \begin{cases} Q_{n+1} & = \tilde{Q} + \frac{1}{2}\left( f_0(\tilde{Q}, \tilde{P}) h + \sum_{i=1}^M f_i(\tilde{Q}, \tilde{P})(\zeta_{i})_n \sqrt{h}\right), \\ P_{n+1} & = \tilde{P}+\frac{1}{2}\left(k_0(\tilde{Q}, \tilde{P}) h + \sum_{i=1}^M k_i(\tilde{Q}, \tilde{P})(\zeta_{i})_n\sqrt{h} \right), \end{cases} \end{split}\\ \Phi_h = \Phi_h^{(2)} \circ \Phi_h^{(1)}
\zeta_h = \begin{cases} & A_h \quad \text{if } ~ \xi>A_h, \\ &-A_h \quad \text{if } ~ \xi<-A_h,\\ & \xi \quad \text{if} ~ |\xi| \leq A_h, \end{cases}
  • Symplectic
  • Equivariant
  • Well-studied

Integration without tears

Stochastic isospectral midpoint:

Take \(Q_n,P_n\) such that \(\mu(Q_n,P_n) = X_n\)

\begin{split} \tilde{\Psi}_{h, n}(\tilde{X}) &= \nabla H_0(\tilde{X})^*h + \sum_{i=1}^M\nabla H_i(\tilde{X})^*(\zeta_i)_n\sqrt{h}, \\ X_n &= \left(I- \frac{1}{2}\tilde{\Psi}_{h, n}(\tilde{X})\right) \tilde{X} \left(I+\frac{1}{2}\tilde{\Psi}_{h, n}(\tilde{X})\right), \\ X_{n+1} &= \left(I+\frac{1}{2}\tilde{\Psi}_{h, n}(\tilde{X})\right) \tilde{X} \left(I- \frac{1}{2}\tilde{\Psi}_{h, n}(\tilde{X})\right). \end{split}

Take \(X_{n+1} = \mu(\Phi_h(Q_n,P_n))\)

Error analysis without tears

Exploit the unreduction!

\begin{split} \mathrm d Q_t &= Q_t\nabla H_0(\mu(Q_t,P_t)) \, \mathrm d t + \sum_{i=1}^M Q_t \nabla H_i (\mu(Q_t,P_t))\circ \mathrm d W_t^i, \\ \mathrm d P_t &= -P_t\nabla H_0(\mu(Q_t,P_t))^* \, \mathrm d t - \sum_{i=1}^M P_t \nabla H_i (\mu(Q_t,P_t))^* \circ \mathrm d W_t^i. \end{split}
~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~ 

Check the literature for error analysis for implicit midpoint

Error analysis with some tears

 

1) Show that the implicit midpoint method does not travel too far:

\(\sup_{h \geq 0} \sup_{n \geq 0} \|Q_n,P_n\| \leq R(Q_0,P_0). \)

2) Truncate the CHS system on \(T^*G\)

Upstairs

Downstairs

3) Apply error analysis from literature

\begin{split} \mathrm d Q_t &= Q_t\nabla H_0(\mu(Q_t,P_t)) \, \mathrm d t + \sum_{i=1}^M Q_t \nabla H_i (\mu(Q_t,P_t))\circ \mathrm d W_t^i, \\ \mathrm d P_t &= -P_t\nabla H_0(\mu(Q_t,P_t))^* \, \mathrm d t - \sum_{i=1}^M P_t \nabla H_i (\mu(Q_t,P_t))^* \circ \mathrm d W_t^i. \end{split}

Reduction by \(\mu\)

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~ 

4) Convergence of method for truncated LP system

  1. Strong convergence: \(\mu\) is Lipschitz
  2. Weak convergence: \(\phi \circ \mu\) is valid test func

5) Truncated LP system = LP system

Recipe:

Error analysis with some tears

  • Assume: \(H_0 \in C^4\) and \(H_1,H_2, \ldots, H_M \in C^5\).
  • \(T>0\): be a fixed final time,
  • \(N \in \mathbb{N}\): number of steps
  • \(X_0 \in \mathfrak{g}^*\): Deterministic initial condition
  • \(\phi \in C^5\): Test function

 

~\sup_{0 \leq n \leq N} \mathbb E\left[ \|X(hn)-X_n\|^2\right]^{1/2} \leq \kappa h^{1/2}\\ \sup_{0 \leq n \leq N} \left|\mathbb E[\phi(X(hn))-\phi(X_n)]\right| \leq \kappa h~

Error analysis with some tears

~\sup_{0 \leq n \leq N} \mathbb E\left[ \|X(hn)-X_n\|^2\right]^{1/2} \leq \kappa h^{1/2}\\ \sup_{0 \leq n \leq N} \left|\mathbb E[\phi(X(hn))-\phi(X_n)]\right| \leq \kappa h~

Geometric structure of equations and its preservation is central. Used to prove

  1. Existence and uniquness
  2. Convergence

Without structure preservation, no convergence guarantees

Mandatory error plots

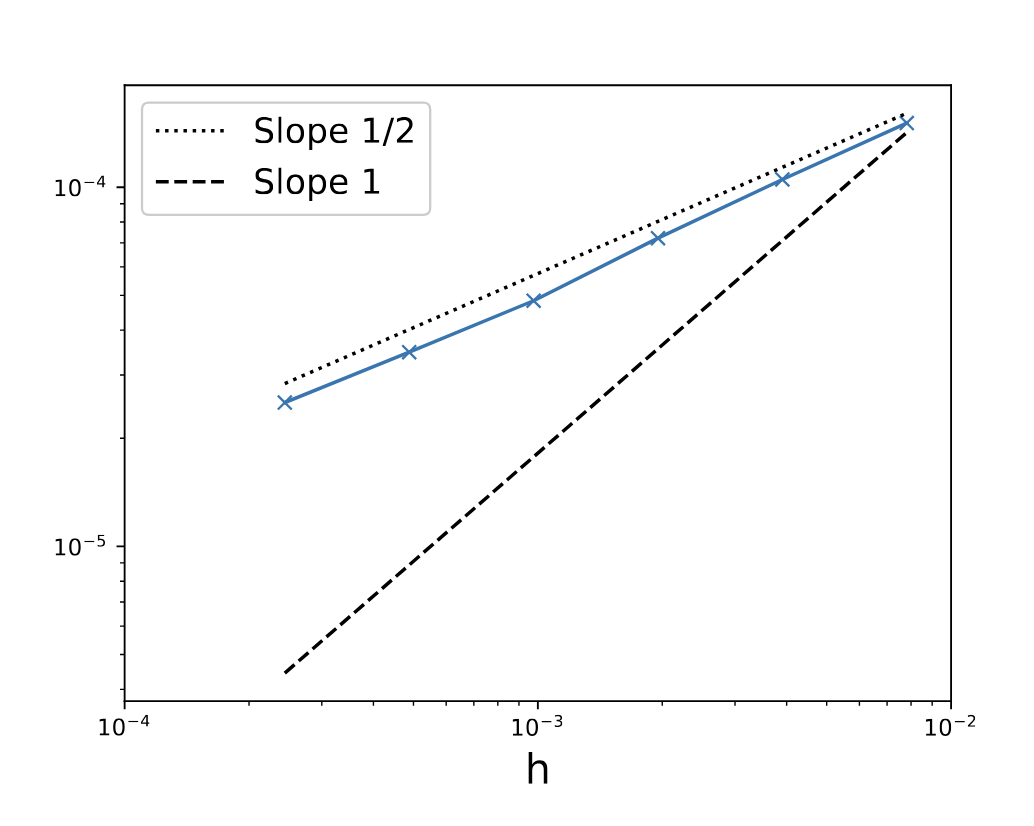
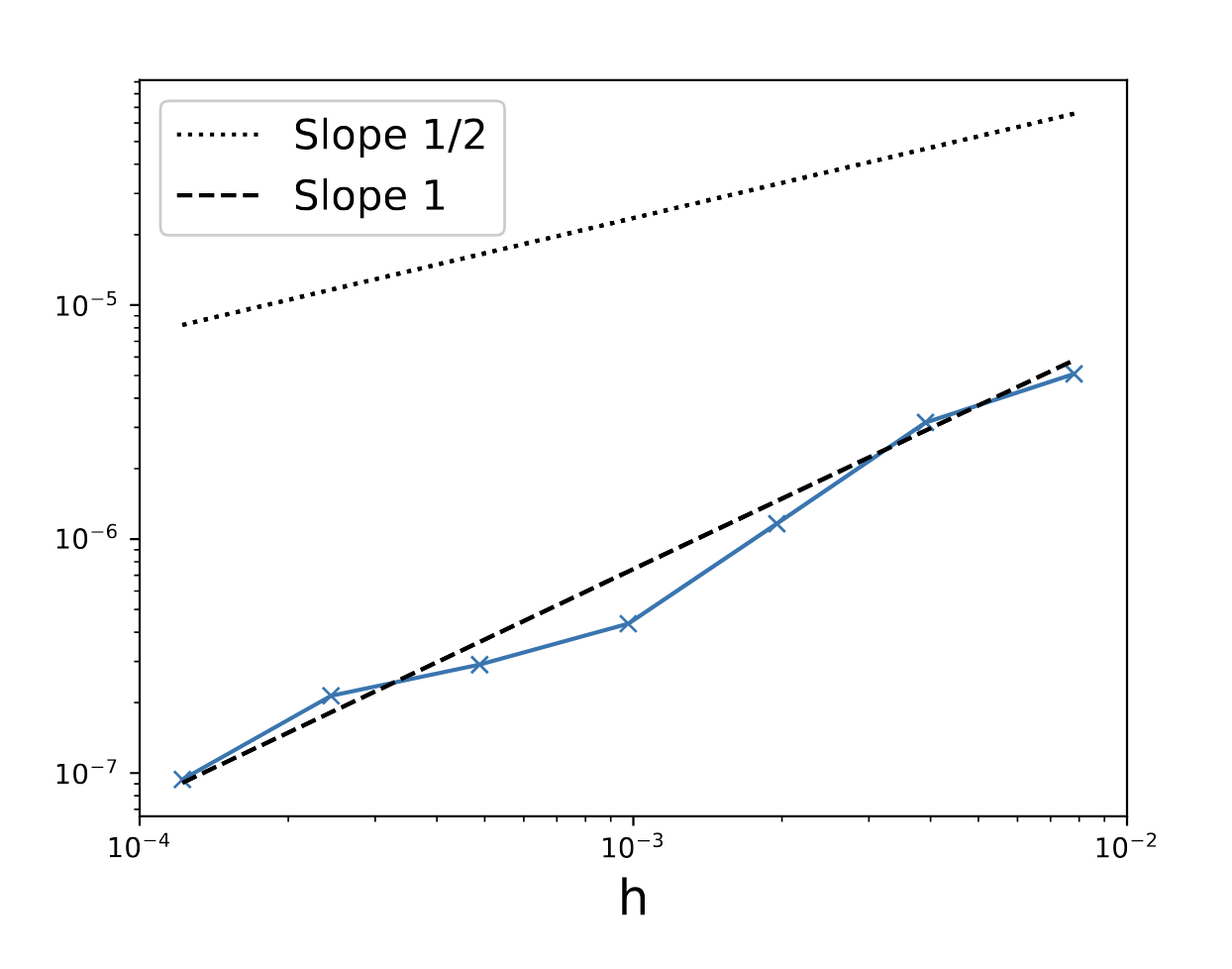
Strong error

Weak error

Rigid body

500 realizations

10^7 realizations

\(\phi(X) = \sin(2\pi x_1) + \sin(2\pi x_2) + \sin(2\pi x_3)\).

Mandatory error plots

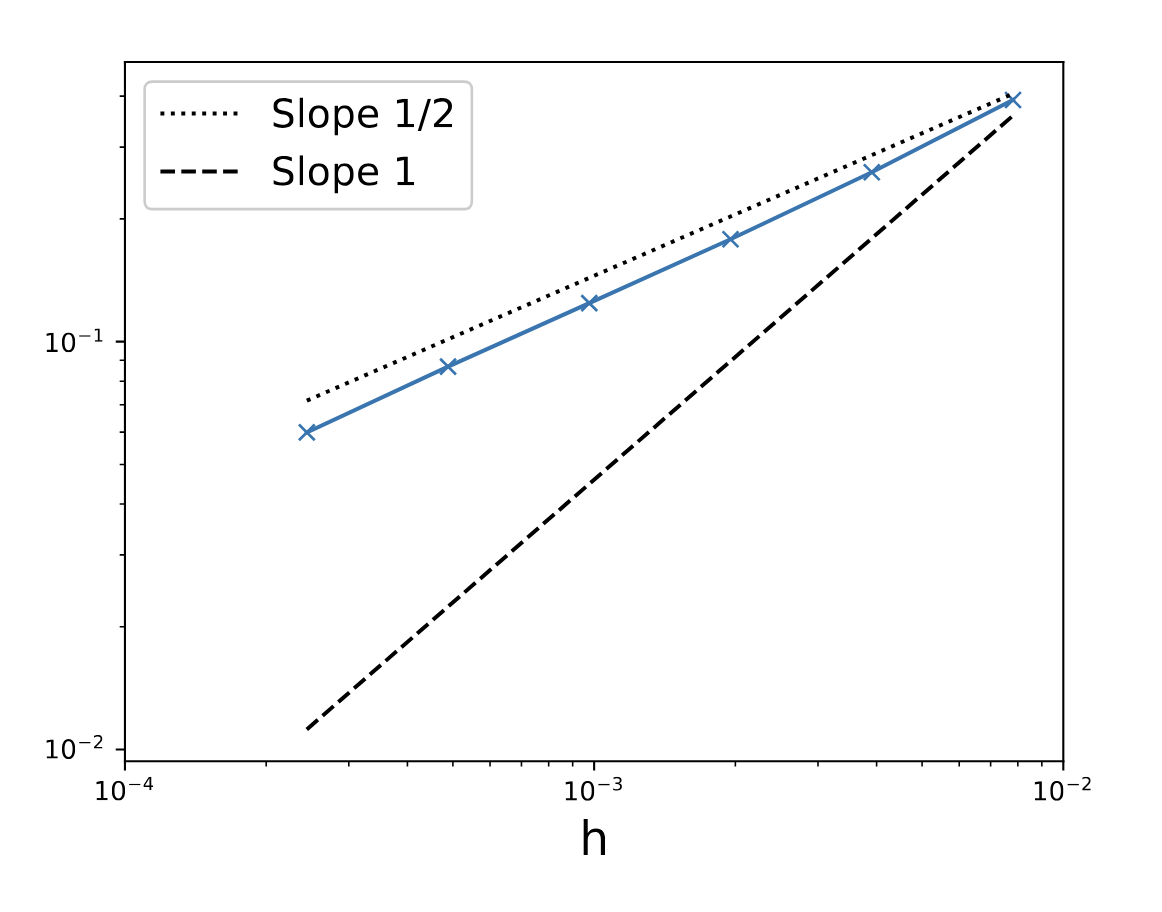
Point vortex dynamics

Strong error

500 realizations

Mandatory error plots

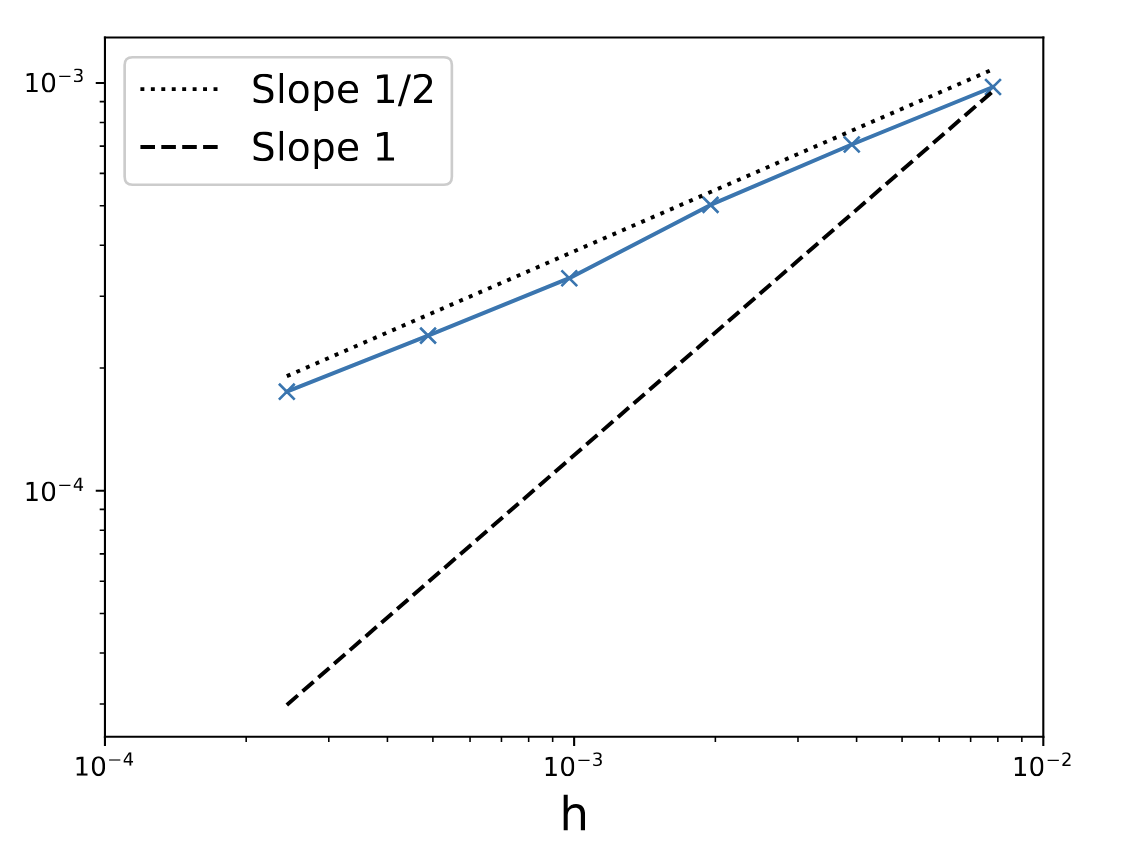
Zeitlin-Euler equations

Strong error

500 realizations

Example of stochastic LP system: outlook

Zeitlin-Euler equations (Sine-Euler on the sphere)

\dot W = -[\Delta_N W, W]

Hamiltonian system: Sample by HMC/PDMP-style method?

Issue: How to jump? Not a canonical system (i.e., "no separation of momentum and position"). Remain in orbit

~ \mathrm d X_t = \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~ 

Probably not the right way... happy for suggestions!

  • We have derived a structure-preserving integrator

  • Geometric proofs of convergence & structure preservation

  • Future work: Make use of the integrator!

  • Regularization by noise
  • Stochastic spin systems
  • Stochastic turbulence