Generating Gaussian random fields using surface finite element methods

Erik Jansson

Slides available at slides.com/erikjansson

Joint work with:

 

  • Mihály Kovács (Pázmány Péter Catholic University/Chalmers)
  • Annika Lang (Chalmers/University of Gothenburg)
  • Mike Pereira (Mines Paris - PSL University)

Made possible by:

 

  1. Bolin, D., Kirchner, K., Kovács, M., Numerical solution of fractional elliptic stochastic PDEs with spatial white noise, IMA J. Numer. Anal., 40(2):1051–1073, 2020 

  2. Dziuk, G., and Elliott, C. M., Finite element methods for surface PDEs. Acta Num., 22:289–396, 2013.

  3. Lang A., Pereira, M., Galerkin–Chebyshev approximation of Gaussian random fields on compact Riemannian manifolds (preprint)

  4. Whittle, P., Stochastic processes in several dimensions. Bull. Inst. Int. Stat., 40:974–994, 1963.

GRFs on manifolds

The SPDE view:  GRFs are solutions to elliptic stochastic partial differential equations on manifolds:

\mathcal{L}u = \mathcal{W}

In this talk: Manifolds = compact, boundary–less 2D embedded surfaces in \(\mathbb{R}^3\) 

Elliptic differential operator

White noise

Two questions:

Computation

Statistics

GRFs on manifolds

The SPDE view:  GRFs are solutions to elliptic stochastic partial differential equations on manifolds:

\mathcal{L}u = \mathcal{W}

In this talk: Manifolds = compact, boundary–less 2D embedded surfaces in \(\mathbb{R}^3\) 

Elliptic differential operator

White noise

Two questions:

Computation

Statistics

GRFs on manifolds

The SPDE view:  GRFs are solutions to elliptic stochastic partial differential equations on manifolds:

\mathcal{L}u = \mathcal{W}

In this talk: Manifolds = compact, boundary–less 2D embedded surfaces in \(\mathbb{R}^3\) 

Elliptic differential operator

White noise

Two questions:

Sampling

Statistics

Main computational tool: FEM

On surfaces!

Step 1: Triangulate the surface

Step 2: FEM space \(S_h \subset H^1(\mathcal{M}_h)\) of p.w., continuous, linear functions

\mathcal{M}
\mathcal{M}_h

Problem 1: Approximate solutions live on \(\mathcal{M}_h\), not \(\mathcal{M}\)!

Given \(\eta: \mathcal{M}_h \to \mathbb{R}\), \(\eta^\ell= \eta \circ p^{-1}\) is on \(\mathcal{M}\)!

Step 3: Key tool in surface finite elements: the lift

Takeway: FEM error similar to flat case, up to a "geometry error" term

Main computational tool: FEM

{\mathcal{T_h}}^\ell
{\mathcal{T_h}}
\nu_{\mathcal{T_h}}
p(x) = x-d_s(x) \nu
x
\nu

Whittle–Matérn fields on the sphere

\(\left(\kappa^2-\Delta_{\mathbb{S}^2}\right)^\beta  u=\mathcal{W}\), \(\beta>1/2, \kappa \neq 0\)

Question: What to do with fractional operator?

Dunford–Taylor integral representation:

(\kappa^2- \Delta_{\mathbb{S}^2})^{-\beta} =\frac{\sin( \pi \beta)}{\pi}\int_{-\infty}^{\infty} e^{2 \beta y} \left( I+e^{2y}(\kappa^2 - \Delta_{\mathbb{S}^2})\right)^{-1} \, \mathrm{d} y\\

Whittle–Matérn fields on the sphere

\(\left(\kappa^2-\Delta_{\mathbb{S}^2}\right)^\beta  u=\mathcal{W}\), \(\beta>1/2, \kappa \neq 0\)

Question: What to do with noise?

\mathcal{W}\sim \sum_{l=1}^\infty\sum_{m=-l}^l a_{l,m}Y_{l,m}
\mathcal{W}_L= \sum_{l=1}^L\sum_{m=-l}^l a_{l,m}Y_{l,m}

Computable by standard SFEM!

(\kappa^2 -\Delta_{\mathbb{S}^2})^{-\beta} \approx Q^{\beta}_k \propto \sum_{l=-K^{-}}^{K^+} e^{2\beta y_{l}}{\left(I+e^{2 y_l}\left(\kappa^2- \Delta_{\mathbb{S}^2}\right)\right)}^{-1} \\

Question: What to do with fractional operator?

Dunford–Taylor integral sinc quadrature:

Whittle–Matérn fields on the sphere

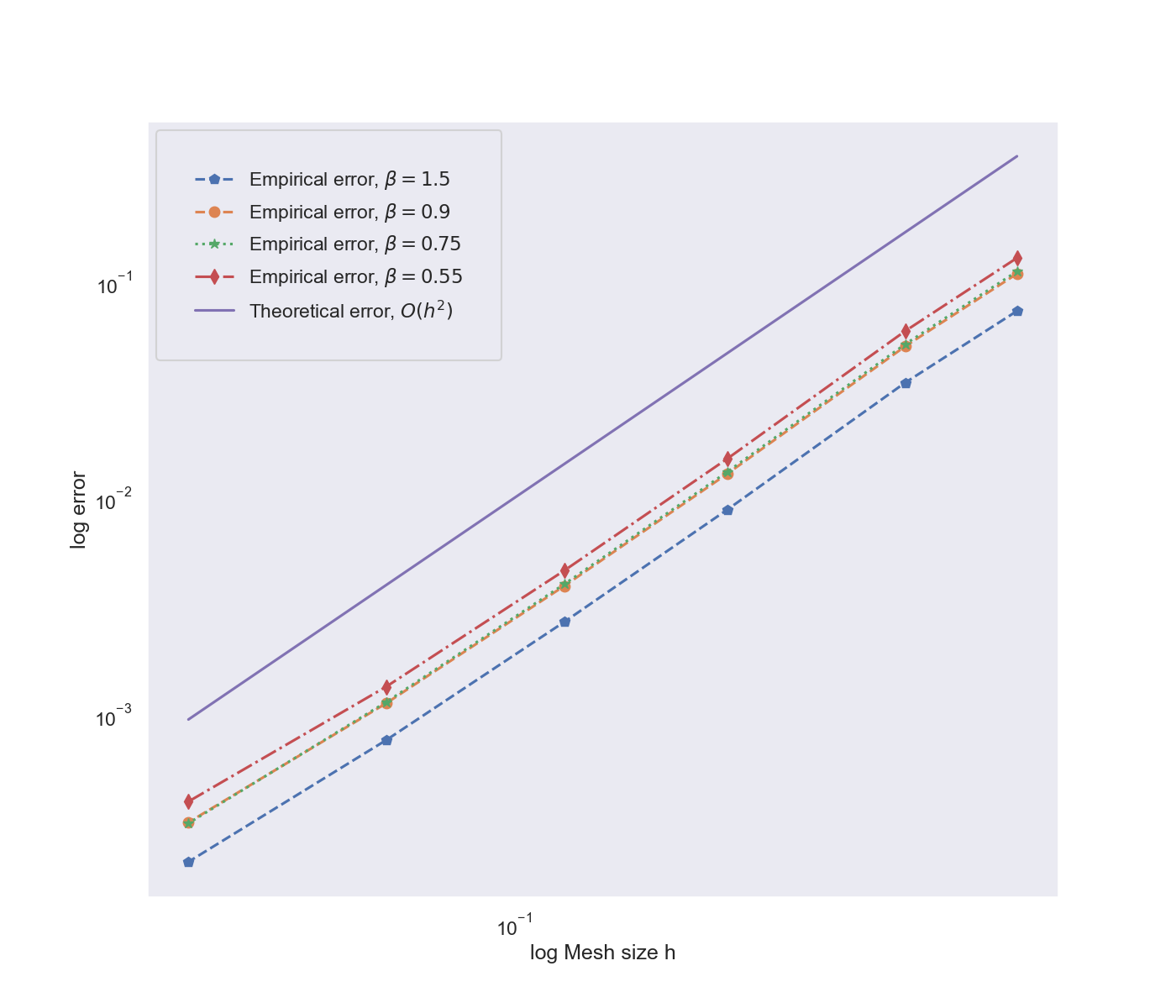
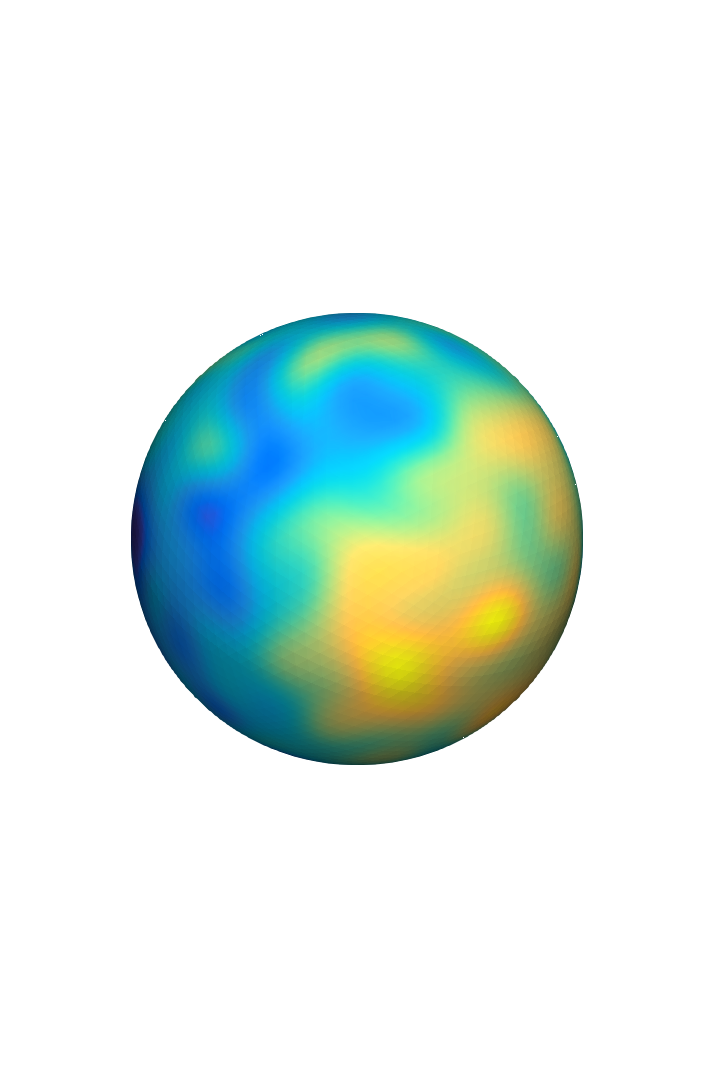
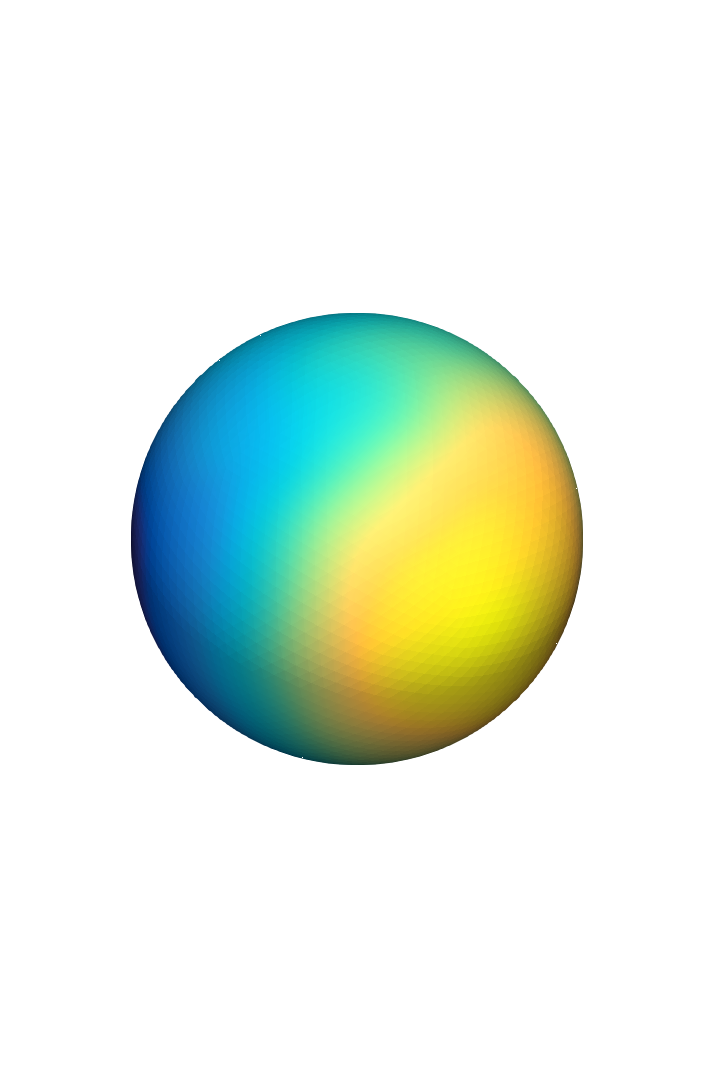
In E.J, Kovács, M & Lang, A, (2022) strong error bounds are proved.

\|u-u_{L,h}^{\ell}\|_* \sim \mathcal{O}(h^2)

Problem: How to approximate noise?

Solution: Different approach...

\mathcal{Z}=\sum_{i\in\N}\gamma(\lambda_{i})W_ie_i

 \((\lambda_i,e_i)\) are eigenpairs of \(\mathcal{L}\) 

Use power spectral density \(\gamma : \mathbb{R}_+\rightarrow \mathbb{R} \)

Random weights \((W_i : i\in\mathbb{N})\) are Gaussian

Problem: Eigenfunctions are not known.

General surfaces: an outlook 

General surfaces: an outlook 

\mathcal{Z}=\sum_{i\in\N}\gamma(\lambda_{i})W_ie_i

Solution (?): Approximation with SFEM basis functions

\mathcal{Z} \approx \sum_{i=1}^{N_h} \gamma(\lambda_{i,h})\overline{W}_i \psi_i

General surfaces: an outlook 

\mathcal{L}(\cdot) = c(x)+\nabla \cdot (A(x)\nabla(\cdot))

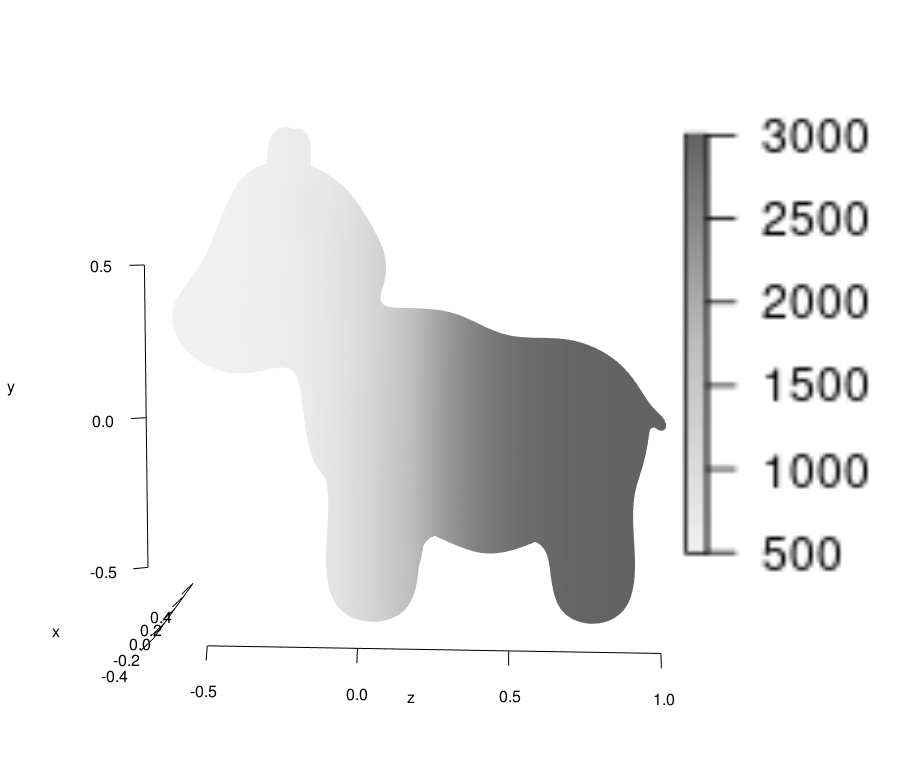
c(x):

small 

large

A(x):

Pullback of \(\R^3\) metric 

 

\begin{bmatrix} 0.1 & 0 & 0\\ 0 & 0.1 & 0 \\ 0&0 & 1 \end{bmatrix}

Inverse correlation length: small values, bigger spots.

Smaller correlation length along \(z\)-axis, elongation in that direction!

General surfaces: an outlook