Vertical gradient flows for optimal transport
Erik Jansson

(Joint work with Klas Modin)
The Monge problem


Geometric structure





In brief: Gradient flow horizontally or vertically

(More info: Modin, 2017 and references therein)
The Gaussian Monge problem
\(\mu_0\) and \(\mu_1\) are both (zero-mean) normal distributions on \(\mathbb{R}^n\).
Normal distributions \(\cong\) \(P(n)\), positive-definite symmetric matrices


Geometric structure
Geometric structure






In brief: Gradient flow horizontally or vertically
Vertical matrix flow



E.J, K. Modin, Convergence of the vertical gradient flow for the Gaussian Monge problem J. Comput. Dyn. (accepted), 2023

How to prove convergence?
Idea: Show \(\frac{\mathrm d} {\mathrm d t} J \to 0\), and that this means we hit polar cone
Questions!
Convergence rate in linear case?
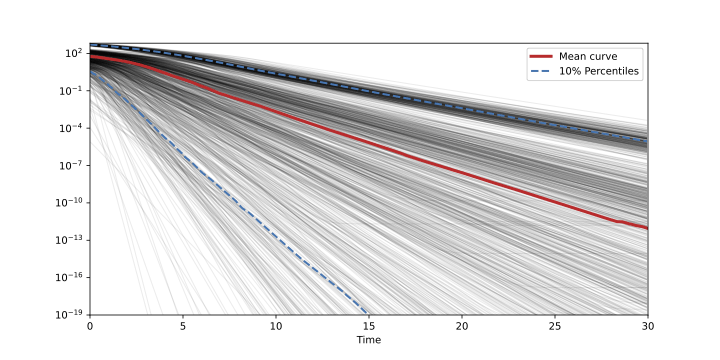
Random matrices with known factorization \(A = PU\), distance to \(B\) from \(P\).
Interesting for other, similar matrix flows.
Questions!
Gaussian case: pre-study for more work into the gradient flows in the infinite-dimensional case?
- Existence? Convergence to minimizer?
- Discretization?