Sub-Riemannian landmark matching and ResNets


Joint work with Klas Modin
ResNets?
Fully-connected equal layers
with a fixed final node
Skip connection \(\implies \) Explicit Euler
ResNets?
Infinite number of layers \(\implies\)
Time-continuous optimal control problem
Skip connection \(\implies \) Explicit Euler
Diffeomorphic shape matching
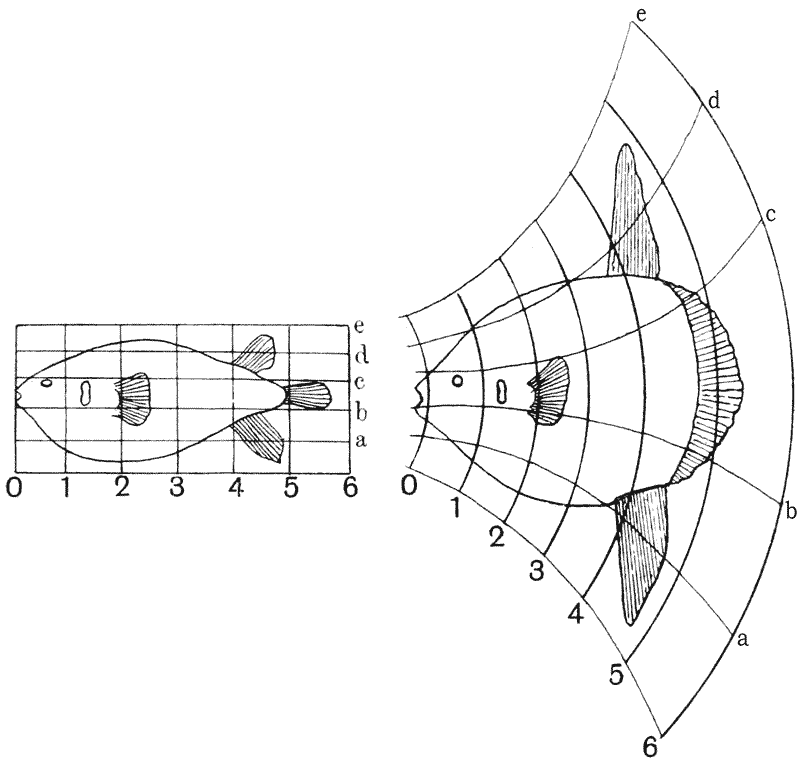

Landmark matching
Landmark matching
Evolve points along a time-dependent vector field!
Which vector field?
Landmark matching
Penalize missing targets:
Penalize weird vector fields:
Key question: How does \(v\) evolve in time?
Landmark matching
Trajectory of \(m_t\) does not care about matching!
Cannonball does not care about target
Landmark matching
Use the Lagrangian \({\int_0^T \int_M Lv(t) \cdot v(t)\mathrm{d}x\mathrm{d}t}_{}\)
Calculus of variations gives:
Modifying landmark matching


Modifying landmark matching


Modifying landmark matching
In usual LM, all vector fields are available
Idea: Constrain set of vector fields
Sub-Riemannian landmark matching!
Modifying landmark matching
\(\mathcal{S}\)
\(v = F(u)(x)\)
\(\mathfrak{X}(M)\)
\(F(u)\)
\(\mathcal{U}\)

\(u\)
Modifying landmark matching
Lagrangian becomes \({\int_0^T \int_M LF(u(t)) \cdot F(u(t))\mathrm{d}x\mathrm{d}t}_{}\)
Points evolve by \(\dot y_i = F(u(t))(y_i)\)
Modifying landmark matching
How to find dynamics of \(u\)?
Idea: Apply chain rule to \(\dot m = \operatorname{ad}_v^T m\)
Modifying landmark matching
\(\mathcal{S}\)
\(v = F(u)(x)\)
\(\mathfrak{X}(M)\)
\(F(u)\)
\(\mathcal{U}\)

\(u\)
Control-affine systems

Simplification of geometry!
- Set \(M=\mathbb{R}^2/(2\pi \mathbb{Z})^2 \)
- Let \(X^i\) be eigenfunctions of toroidal Laplacian
Computational example
Control-affine systems
- Initial guessof inital control \(u^{[0]}_0\)
- Evolve \(u^{[0]}_0\) and landmarks
- Evaluate energy functional \(E\).
- Update control by \(u^{[1]}_0 \leftarrow u^{[0]}_0-\epsilon \nabla_{u^{[1]}_0}E\)
Computational example
"Adjust initial conditions until target is hit"
Control-affine systems
Goal: Move landmarks from one fish to the other




Control-affine systems
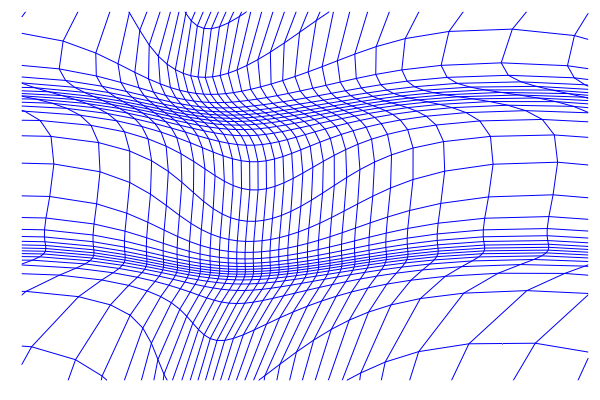
Control-affine systems
Goal: Move landmarks on torus to \([0,1]\)
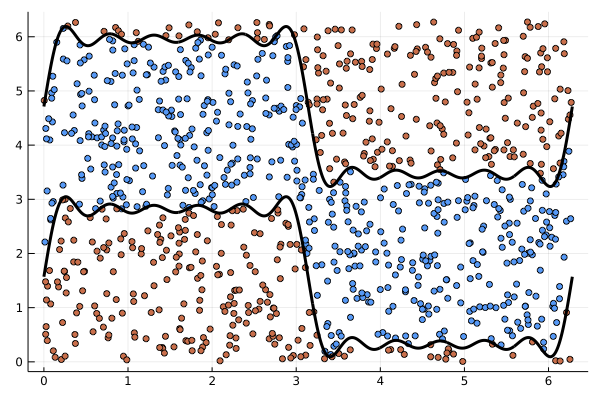
Projection
Control-affine systems
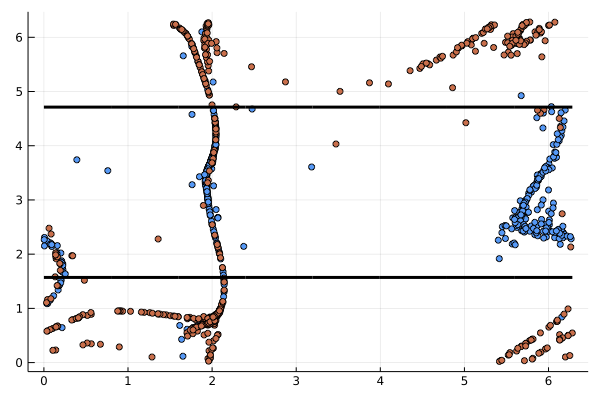

Badly behaved transformation!
Increase regularization strength?
Control-affine systems
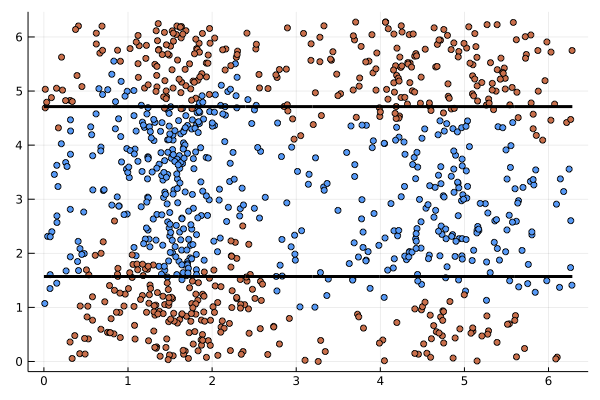
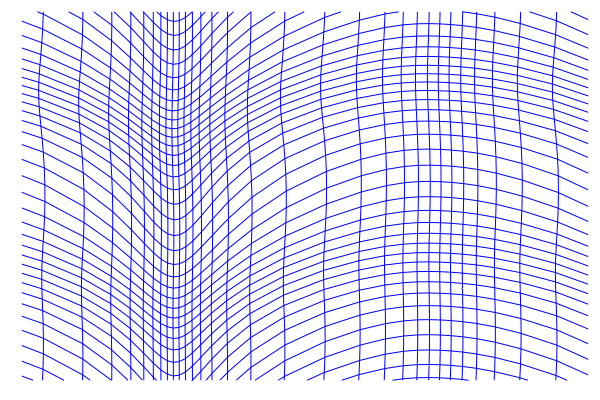
Control-affine systems
Why study sR-LM?
When matching landmarks, points are moved by a vector field parametrized by some control variable.
A neural networks moves points along a vector field determined by weights and biases.
- Landmarks
- Image
- Shooting
- Warping new landmarks
- Control parameters
- Input data, e.g. images
- "Meta-image"
- Training network
- Testing
- Weights and biases
View networks with shape analysis glasses!
Why study sR-LM?
Why study sR-LM?
Available vector fields:
Iterated Lie brackets
If distribution is integrable, we
move only along blue line
To have reachability, we must destroy integrability
\(\implies\) Nonlinearity!

Move from
to
-
We can parametrize landmark matching and retain geometric framework
-
There is a connection to neural networks
-
Future work: leverage connection for concrete AI applications