Geometric shape matching for single-particle Cryo-EM data

 

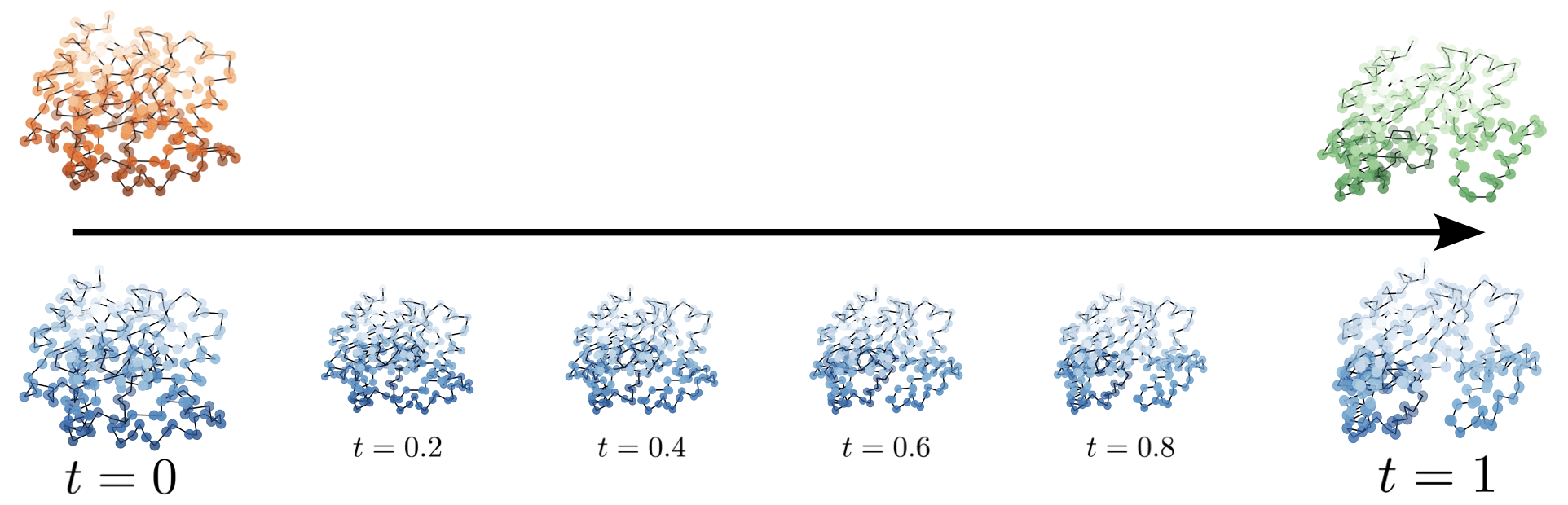
slides.com/erikjansson

Joint work with:

 

  • Klas Modin (Chalmers/University of Gothenburg)
  • Ozan Öktem (Royal Institute of Technology, Stockholm)
  • Jonathan Krook (Royal Institute of Technology, Stockholm)

Talk based on:

asdasdasd

 

 

arXiv:2410.00833 

But what is a shape?

Shape analysis

Point cloud on torus

Function on \([0,1]^2\)

Density on \([0,1]\)

Anything a diffeomorphism can act on!

What is a shape?

A warp is determined by a time-dependent vector field \(v\)

A vector field generates a curve of diffeomorphisms \(\gamma: [0,1] \mapsto G = \operatorname{Diff}(M)\) by

\(\dot \gamma(t) = \nu(t, \gamma(t)), t \in [0,1], \gamma(0) = \operatorname{Id} \)

The optimal vector field is a minimizer of an energy!

What is an optimal warp?

The energy functional

\underbrace{\mathcal{D}(\gamma(1).A,B)}_{\text{Matching energy}}+\underbrace{d_G(\gamma,e)}_{\text{Regularization}}

Canonical choice! Use right-invariant metric

\underbrace{\mathcal{D}(\gamma(1).A,B)}_{\text{Matching energy}}+\underbrace{\int_0^1 \int_M L\nu(t) \cdot \nu(t)\mathrm{d}x\mathrm{d}t}_{\text{Regularization}}

The energy functional

\underbrace{\mathcal{D}(\gamma(1).A,B)}_{\text{Matching energy}}
+\hspace{2.4pt}\underbrace{\int_0^1 \int_M L\nu(t) \cdot \nu(t)\mathrm{d}x\mathrm{d}t}_{\text{Regularization}}

Only depends on final value of \(\gamma(t)\)

Changes depending on application

The energy functional

Only depends on final value of \(\gamma(t)\)

Depends on whole path

Changes depending on application

Key question: How does \(\nu\) evolve?

(Answer: Use calculus of variations, but with which energy?)

\underbrace{\mathcal{D}(\gamma(1).A,B)}_{\text{Matching energy}}
+\hspace{2.28pt}\underbrace{\int_0^1 \int_M L\nu(t) \cdot \nu(t)\mathrm{d}x\mathrm{d}t}_{\text{Regularization}}

The energy functional

 Evolution of vector field does not care about matching!

Cannonball does not care about target

Shooting analogy

Use the Lagrangian \({\int_0^T \int_M L\nu(t) \cdot \nu(t)\mathrm{d}x\mathrm{d}t}_{}\) 

Calculus of variations gives:

~\dot m = \operatorname{ad}_v^* m~ \\ m = L\nu

The EPDiff equation

Matching by shooting

A picture says more...

~\dot m = \operatorname{ad}_\nu^* m~ \\ m = L\nu

Shape analysis made simpler

The ingredients you really need:

A Lie group of deformations \(G\) acting on a set of shapes \(V\) (metric space)

\mathcal{D}(\gamma(1).A,B)

Flexible choice

\langle \dot \gamma, \dot \gamma\rangle_\gamma = (\dot \gamma \circ \gamma^{-1}, \dot \gamma \circ \gamma^{-1})_{\mathfrak{g}}

Right-invariant metric (not so flexible)

Shape: indirect matching

Here, \(A\) and \(B\) are assumed to be elements in the same space.

 

What if we cannot directly observe B?

Shape: indirect matching

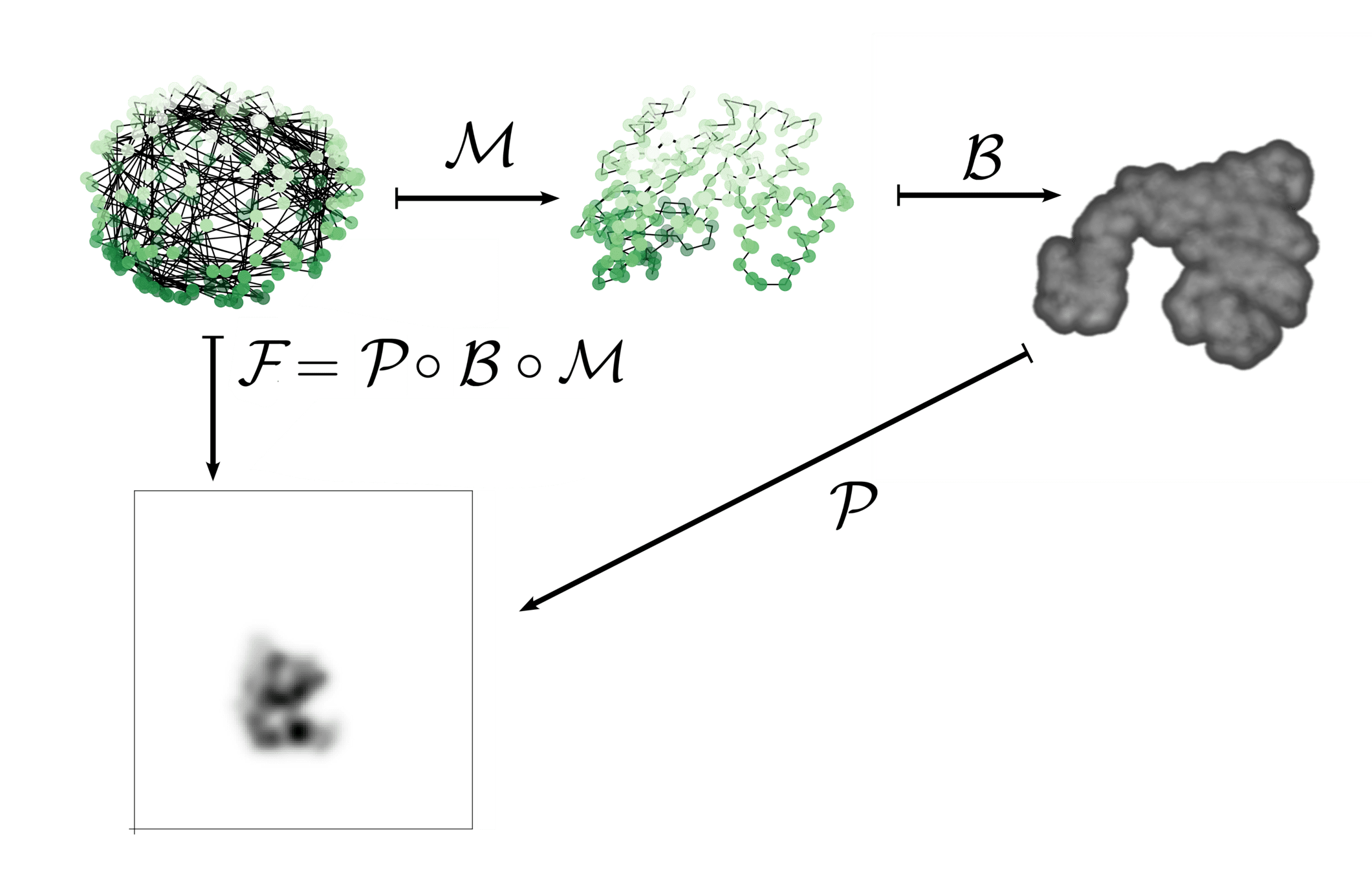
Include a forward operator \(\mathcal{F}\colon V \to W\)

\underbrace{\mathcal{D}_W(\mathcal{F}(\gamma(1).A),B)}_{\text{Matching energy}}+\underbrace{\int_0^1 \int_M L\nu(t) \cdot \nu(t)\mathrm{d}x\mathrm{d}t}_{\text{Regularization}}

Initial shape: \(A \in V\)

Target shape: \(B \in W\)

Doesn't affect mathematical framework!

"Reconstructs" the \(\gamma(1).A\) that best would map to \(B\)

Shape for Cryo-EM

Single-particle Homogeneous Cryo-EM in 30 seconds (by a maths person)

Electron

microscope

Low dose - low SnR

Many images

Shape for Cryo-EM

Proteins in 30 seconds (by a mathematician)

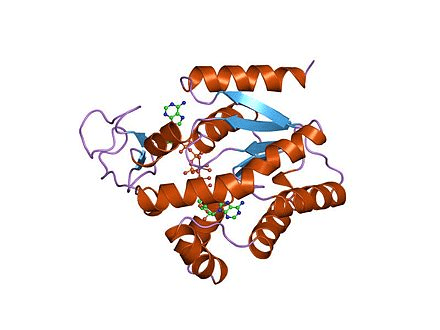
In this work: forget about everything but the \(C_\alpha\)s

Relative positions

Shape for Cryo-EM

Shape space: space of relative positions \(V = \mathbb{R}^{3N}\)

Data space - 2D images, \(L^2(\mathbb{R}^2)\) (very noisy!)

However: We want rigid deformations, so \(G = \operatorname{SO}(3)^N\), and \(\operatorname{dim}(G) \ll \operatorname{dim}(\operatorname{Diff}(M)) = \infty\)

Todo: Construct forward model, decide on energy, compute gradients, set up optimization routine

Shape for Cryo-EM

Forward model building

Shape for Cryo-EM

Forward model building

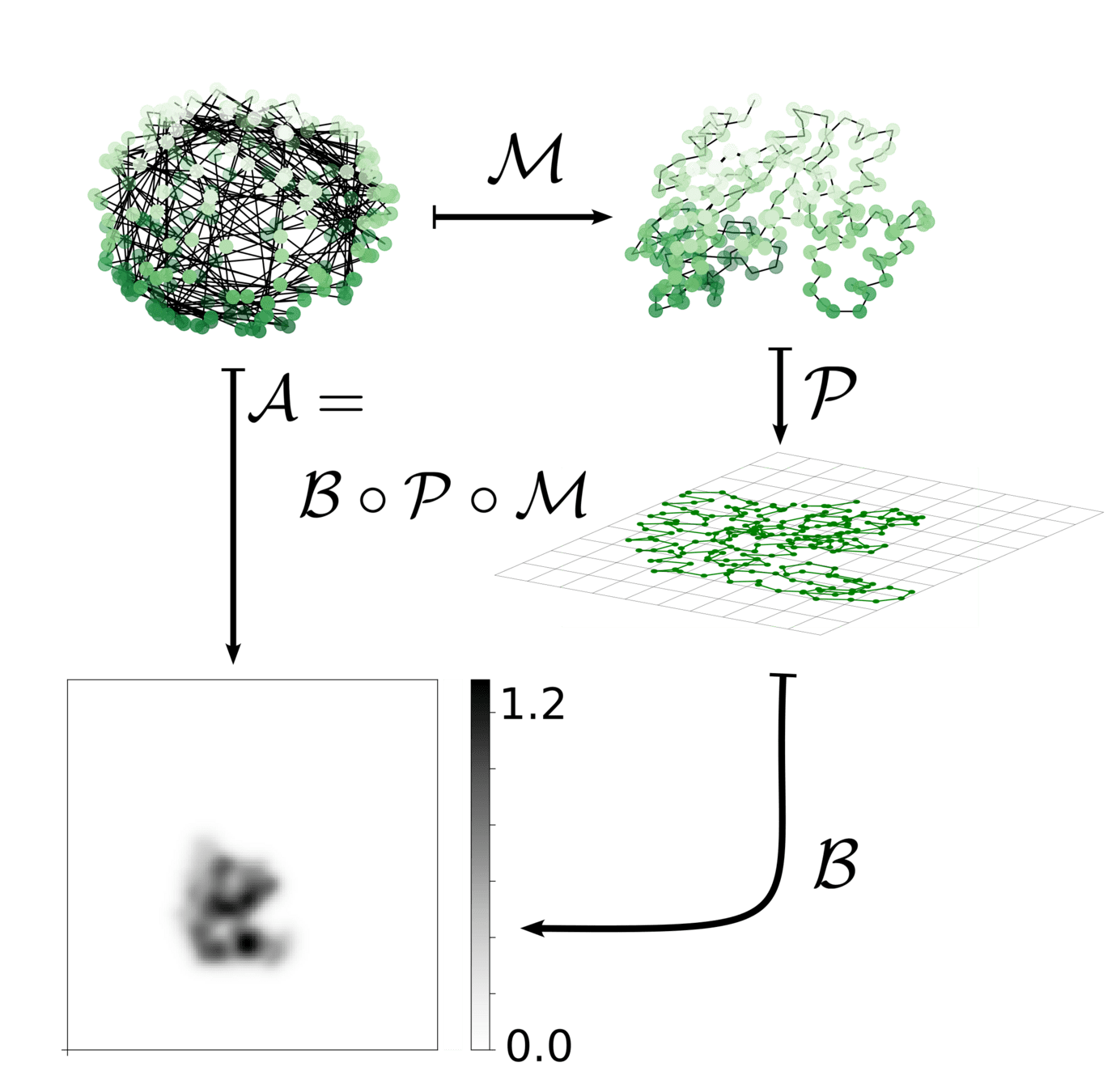
Shape for Cryo-EM

Similarity score is clear. For now: use x-y-z projections (3 images)

\mathcal E(\nu) = \frac{1}{2} \sum_{i \in \{1,2,3\}}\left\| \mathcal{F}_i(\Phi(\gamma(1),w)) - y_i \right\|^2_{L^2(\mathbb R^2)} + \lambda \int_0^1 \operatorname{Tr}(\nu^T\mathbb{I}\nu)\\ \dot \gamma = \nu \gamma, \gamma(0) = e

Shape for Cryo-EM

Similarity score is clear. For now: use x-y-z projections (3 images)

\dot m = [m,\nu] \\ m = \mathbb{I} \nu \\ \dot \gamma = \nu \gamma, \gamma(0) = e
  • Guess \(\nu(0)\) (or path sampled at discrete points)
    • Integrate
    • Evaluate \(\mathcal{E}\) and compute \(\nabla_{\nu(0)} \mathcal{E}\)
  • Update \(\nu(0)\) with favorite algorithm (A few GD steps and then L-BFGS-B)

 

Gradient is available (even easy to compute)

(but ugly)

Shape for Cryo-EM

Gradient is available

Shape for Cryo-EM

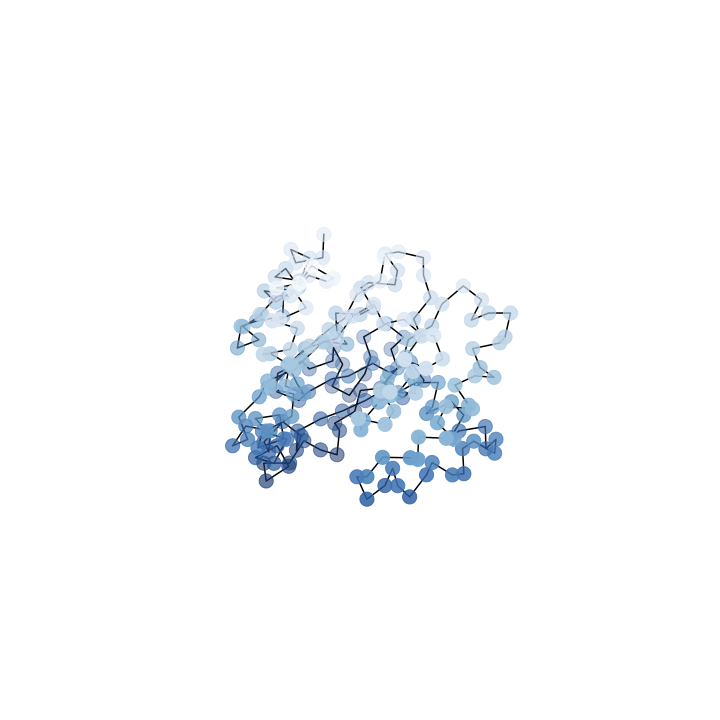
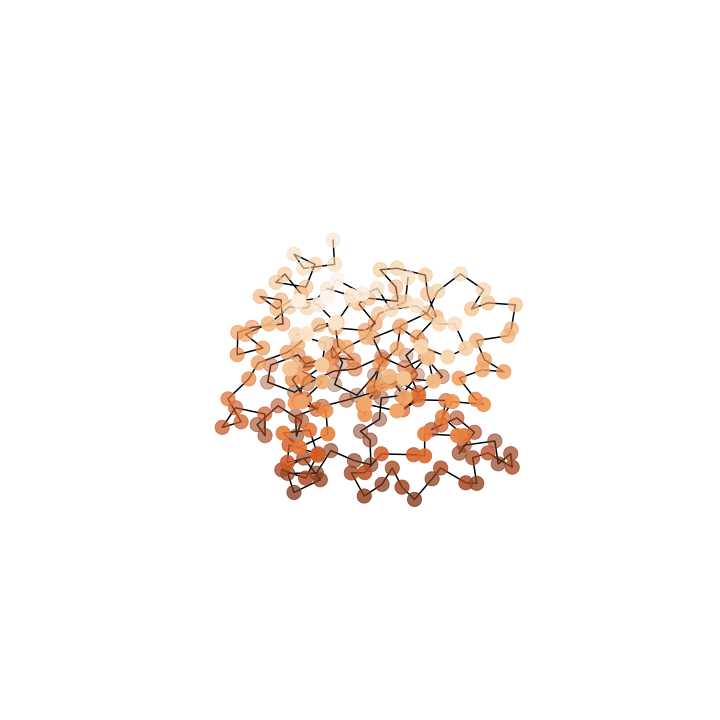
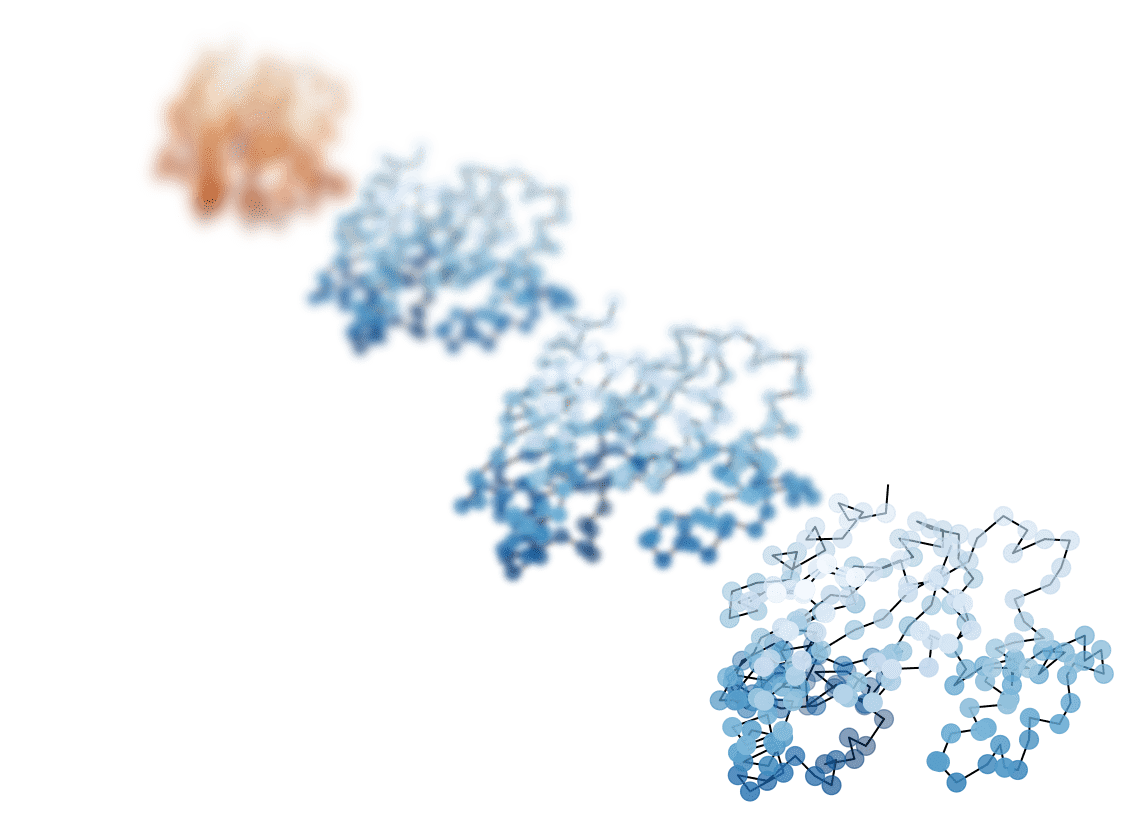
Deformation

What we want

What we see

Where we start

Shape for Cryo-EM

Oh no

but....

Shape for Cryo-EM

x

y

z

Deformed

Target

Template

Shape for Cryo-EM

Shape for Cryo-EM

Hope!

Turn up number of images used

3 \rightarrow 300

Decent in the directions we have projections

Shape for Cryo-EM

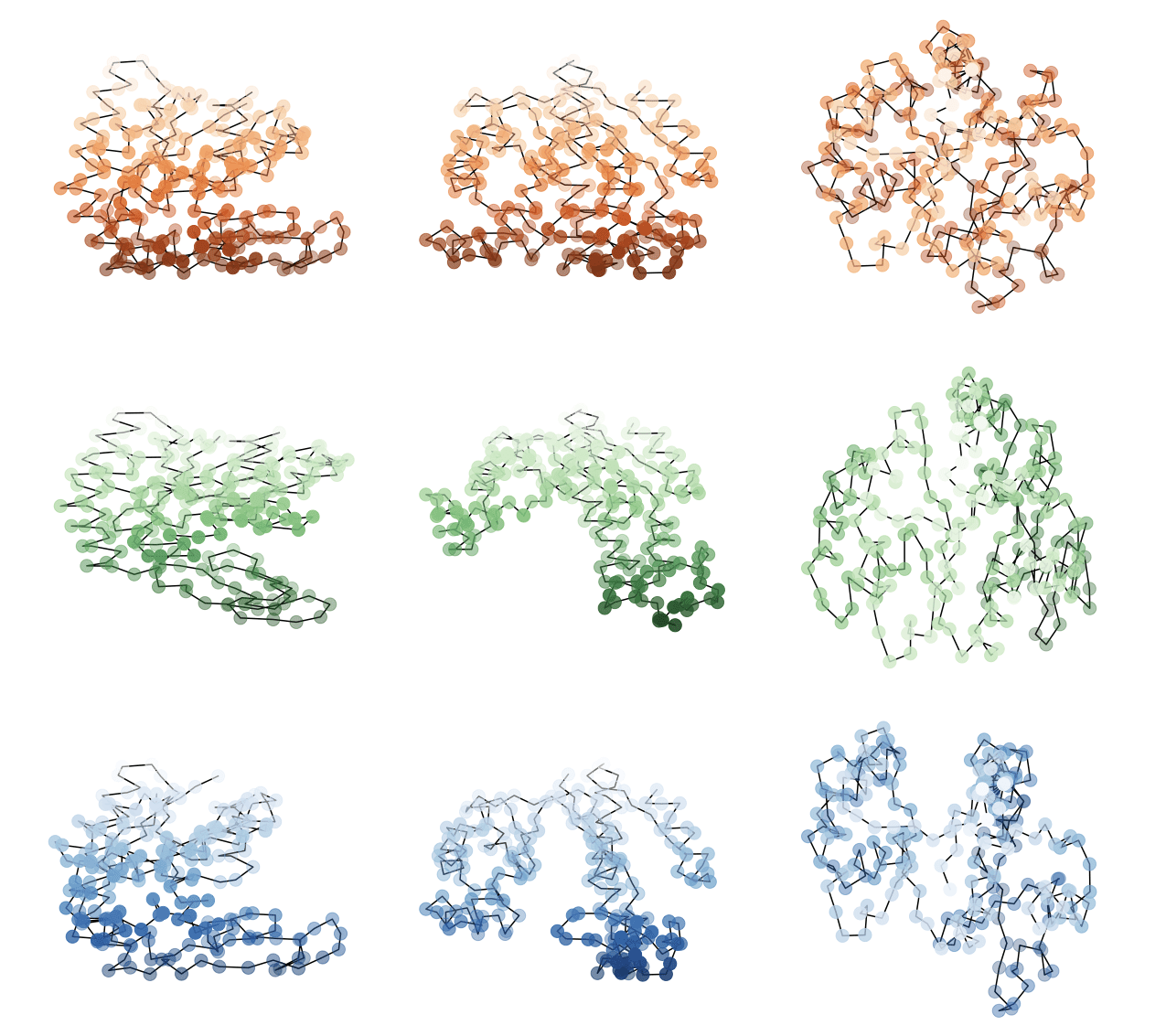
Deformation

What we want

What we see

Where we start

Shape for Cryo-EM

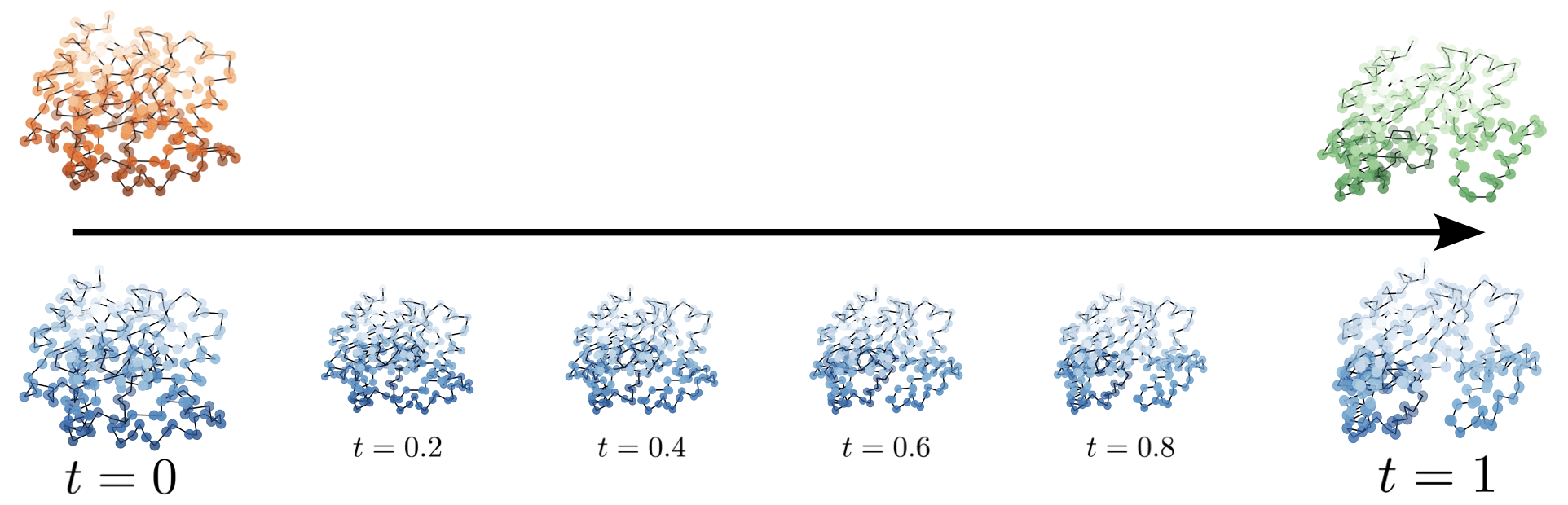
Deformation path

Note: Deformation makes no physical sense

Shape for Cryo-EM

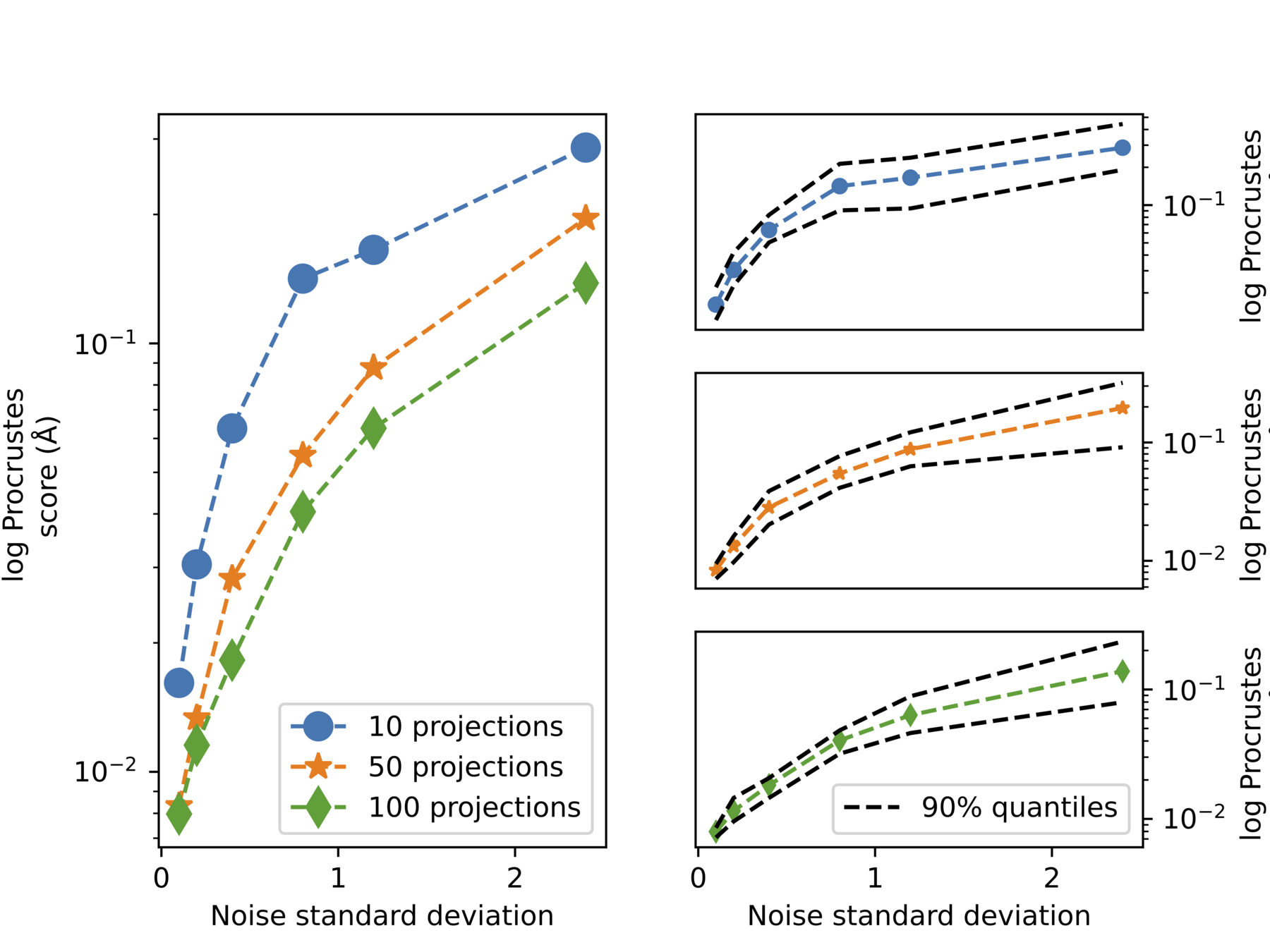
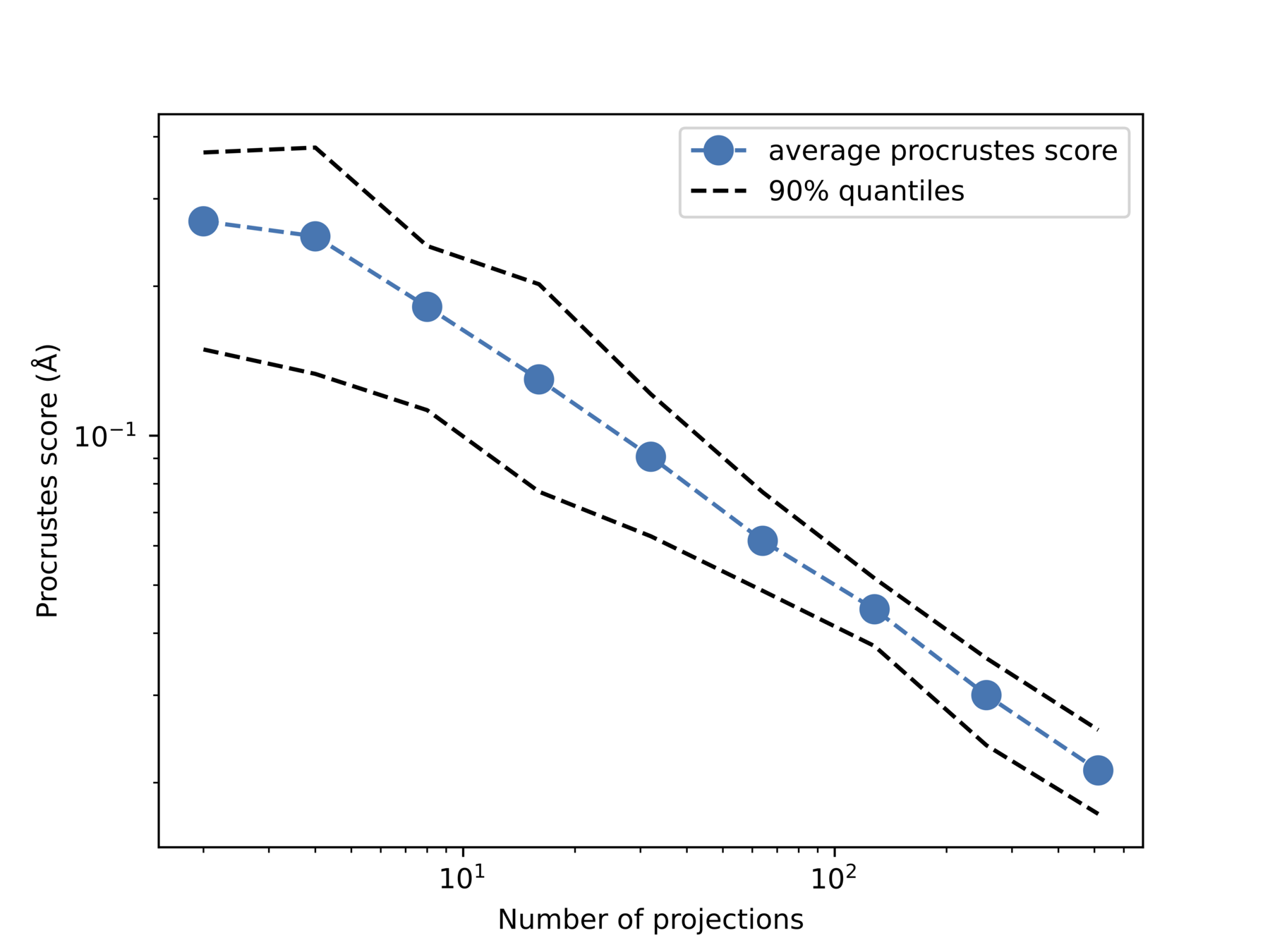
Increase noise

Increase #projections

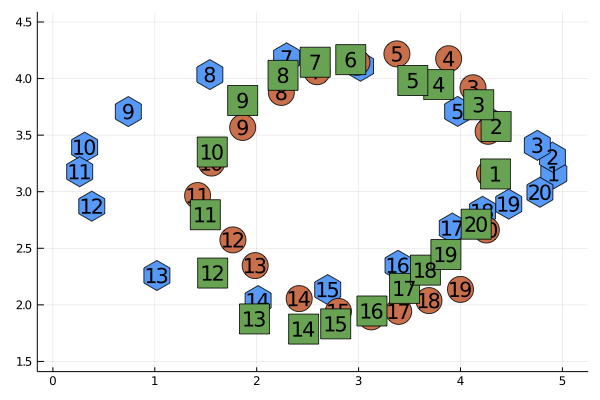
Quantative measure: Procrustes score

 Procrustes analysis

Two point clouds \(\mathbf x = (x_i)_{i=1}^K\) and \(\mathbf y = (y_i)_{i=1}^K\)

Rotate, reflect, scale and translate ("superimpose") \(\mathbf x\) to be as close in mean-square sense to \(\mathbf y\) as possible

As close as we can get: Procrustes distance (early statistical shape analysis measure)

In conclusion: Early days...

  • Global pose: We assume it is known
     
  • Side chains: We cut away the side chains
     
  • Faster methods: Even if we have the gradient, not fast!

Shape analysis seems promising