Geometric numerical methods: from random fields to shape matching

Geometric numerics?

Numerical analysis: the art of being wrong in the mathematically correct way

Concerned with the approximate solution of continuous problems

Geometry: the study of space: distance, shape, size, angles...

Geometric numerics: How to approximate solutions to geometric problems

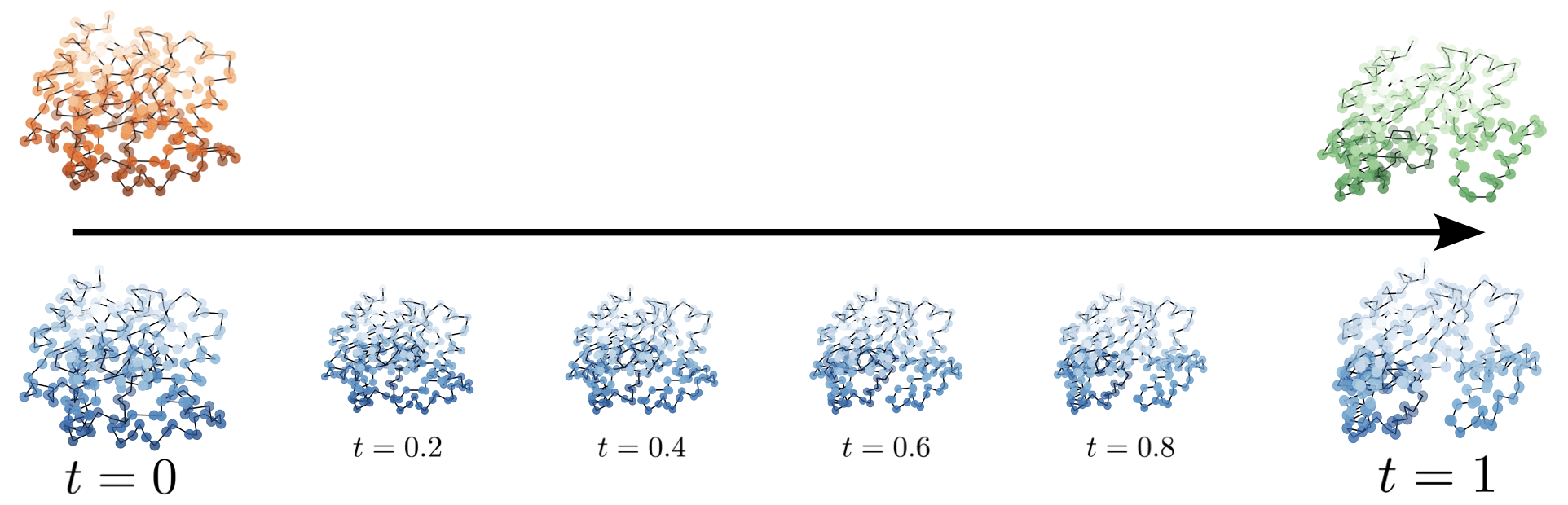
Shape analysis and matching problems

Structure-preserving numerics for geometric mechanics

Elliptic SPDEs on manifolds
for sampling of random fields

GEOMETRIC

NUMERICAL

METHODS

Random fields via stochastic partial differential equations

Paper I and II research questions

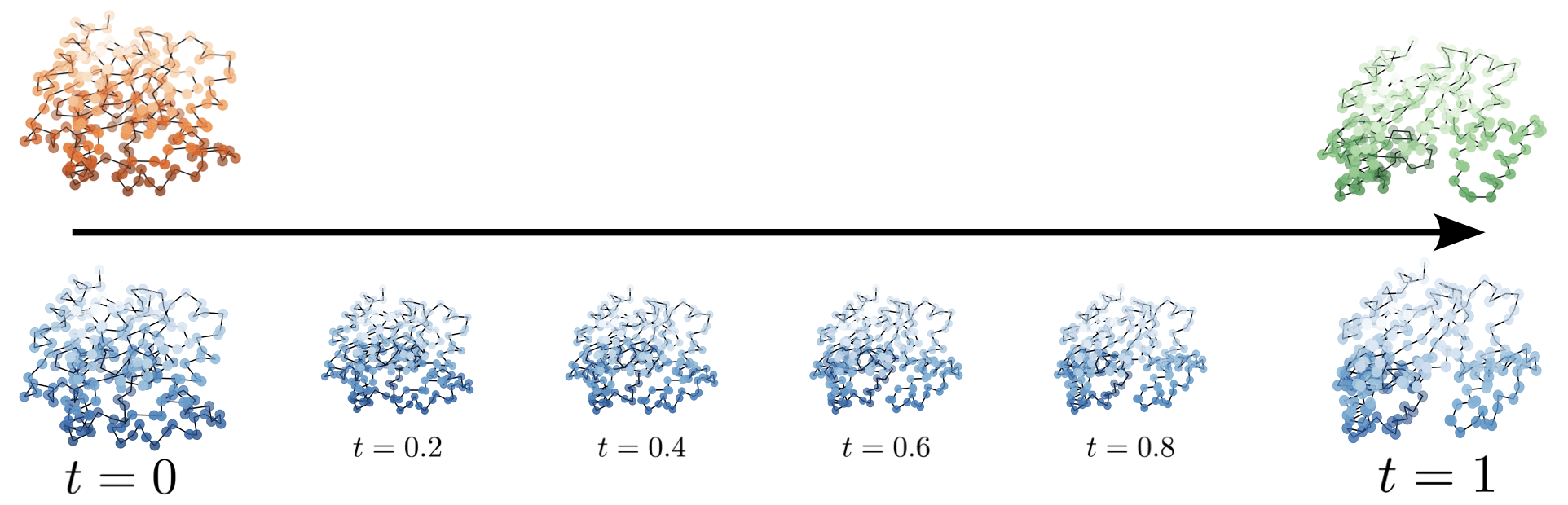
What is a random field?

Definition: Stochastic process indexed by spatial domain: Assigns random value to each point on domain

We consider Gaussian random fields on surfaces generated by coloring white noise with linear operators that are functions of differential operators.

Our models

\mathcal Z = (\kappa^2-\Delta_{M})^{-\beta} \mathcal W

Classical model inspired by the commonly used Matérn kernel. Whittle–Matérn fields.

\mathcal Z = \zeta(\mathcal L) \mathcal W

Novel, more flexible model proposed by us

Contains Whittle–Matérn fields.

Research questions and approaches

Statistics phrasing: How to sample the fields?

Numerics phrasing: How to approximately solve for \(\mathcal Z\)

Two approaches

Paper I

Paper II

Restricted to sphere
Approximate fractional part with quadrature
Solve family of systems recursively with FEM

Main scientific question: Convergence of method

Hypersurfaces in \(d = 2,3\)
Approximate white noise on FEM space
Color approximated white noise with projected operators

Both fundamentally based on surface FEM methods

Main scientific question: Convergence of method

Shape analysis

and matching problems

paper IV and VI research questions

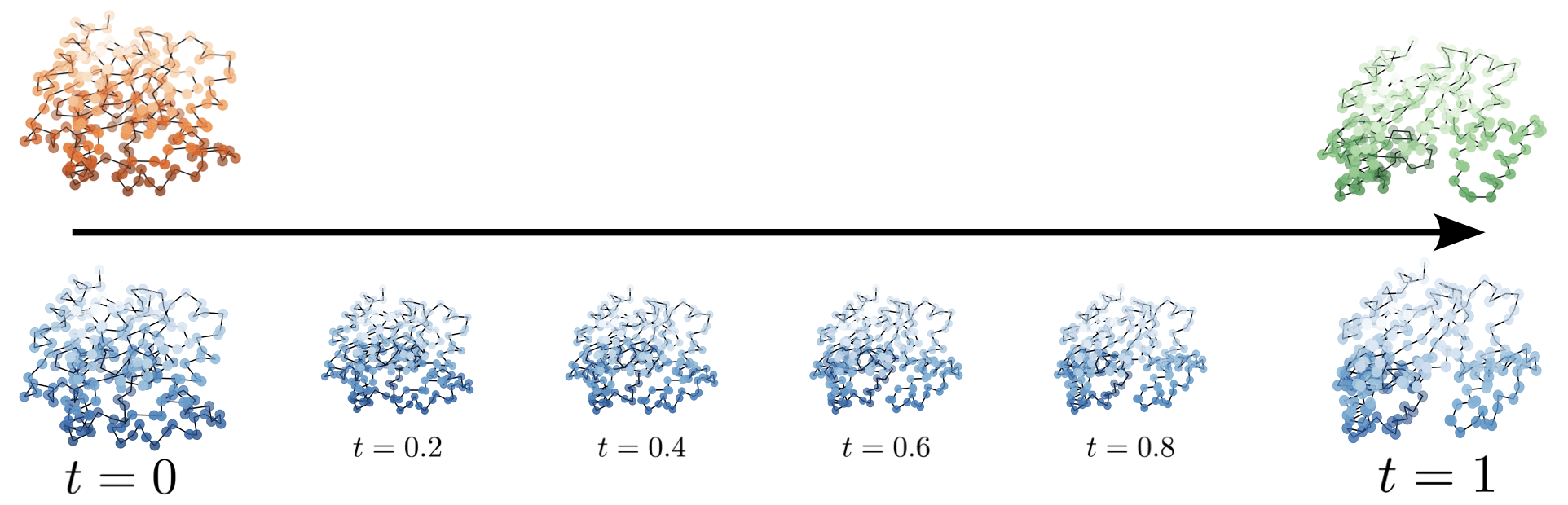
Shape analysis

But what is a shape?

Point cloud on torus

Function on \([0,1]^2\)

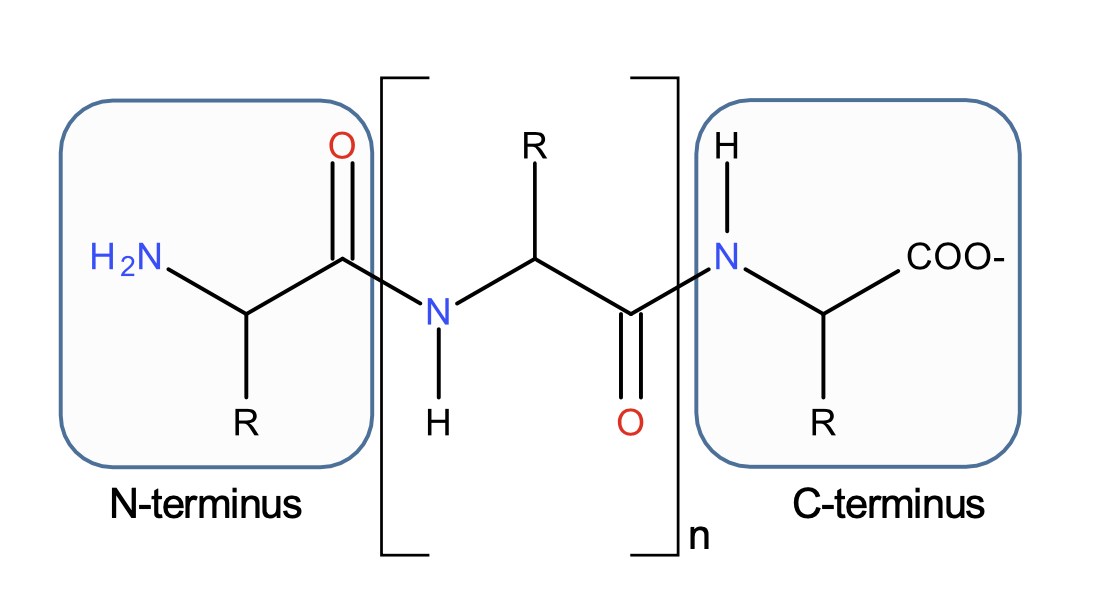
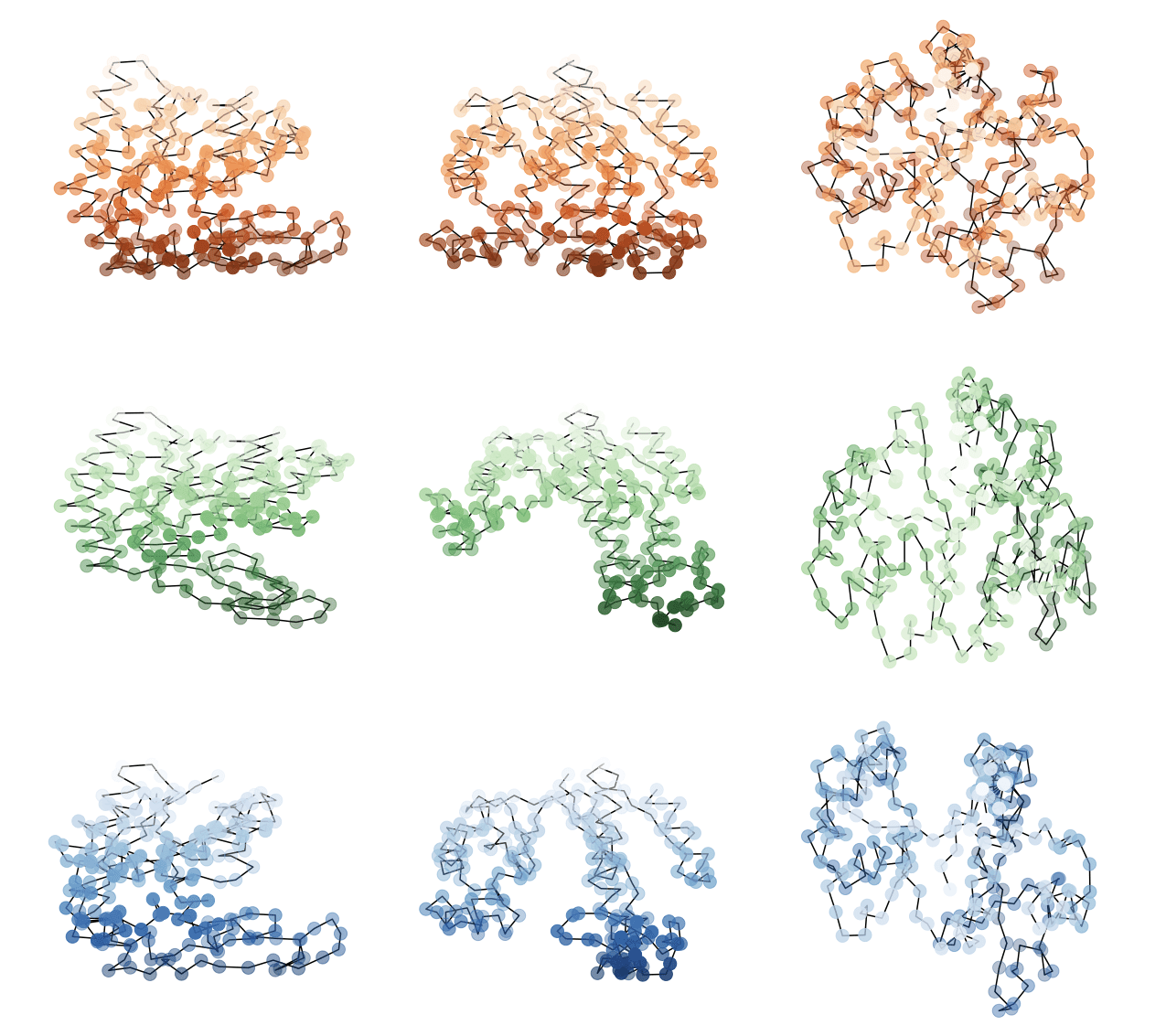
A protein backbone

Shapes are in a (metric) space \(V\) acted upon by a Lie group of deformations \(G\).

\(V = (\mathbb{T}^2)^N\),

\(G = \operatorname{Diff}(\mathbb{T}^2)\)

\(V = C^\infty([0,1]^2)\),

\(G = \operatorname{Diff}([0,1]^2)\)

\(V = \mathbb{R}^{3N}\),

\(G = \operatorname{SO}(3)^N\)

Matching is an optimization problem

Deformations \(g\) is endpoint of curve \(\gamma \colon [0,1] \to G \)

\dot \gamma_\nu(t) = \mathrm d R_{\gamma_\nu(t)} {\color{black}\nu(t)},\quad \gamma_\nu(0) = e

\min_{\gamma} \left(d^2_V(\gamma_\nu(1) \cdot A, B)+\lambda \int_0^1 \langle \dot \gamma_\nu(t) ,\dot \gamma_\nu(t)\rangle_{\gamma(t)} \mathrm d t\right)

Right-invariance of metric

\min_{\nu} \left(d^2_V(\gamma_\nu(1) \cdot A, B)+\lambda \int_0^1 \langle \nu(t) , \nu(t)\rangle_{e} \mathrm{d}t\right)

In thesis: indirect matching

What if \(A\) and \(B\) are not in the same space?

Application: Indirect observation of B?

Indirect matching

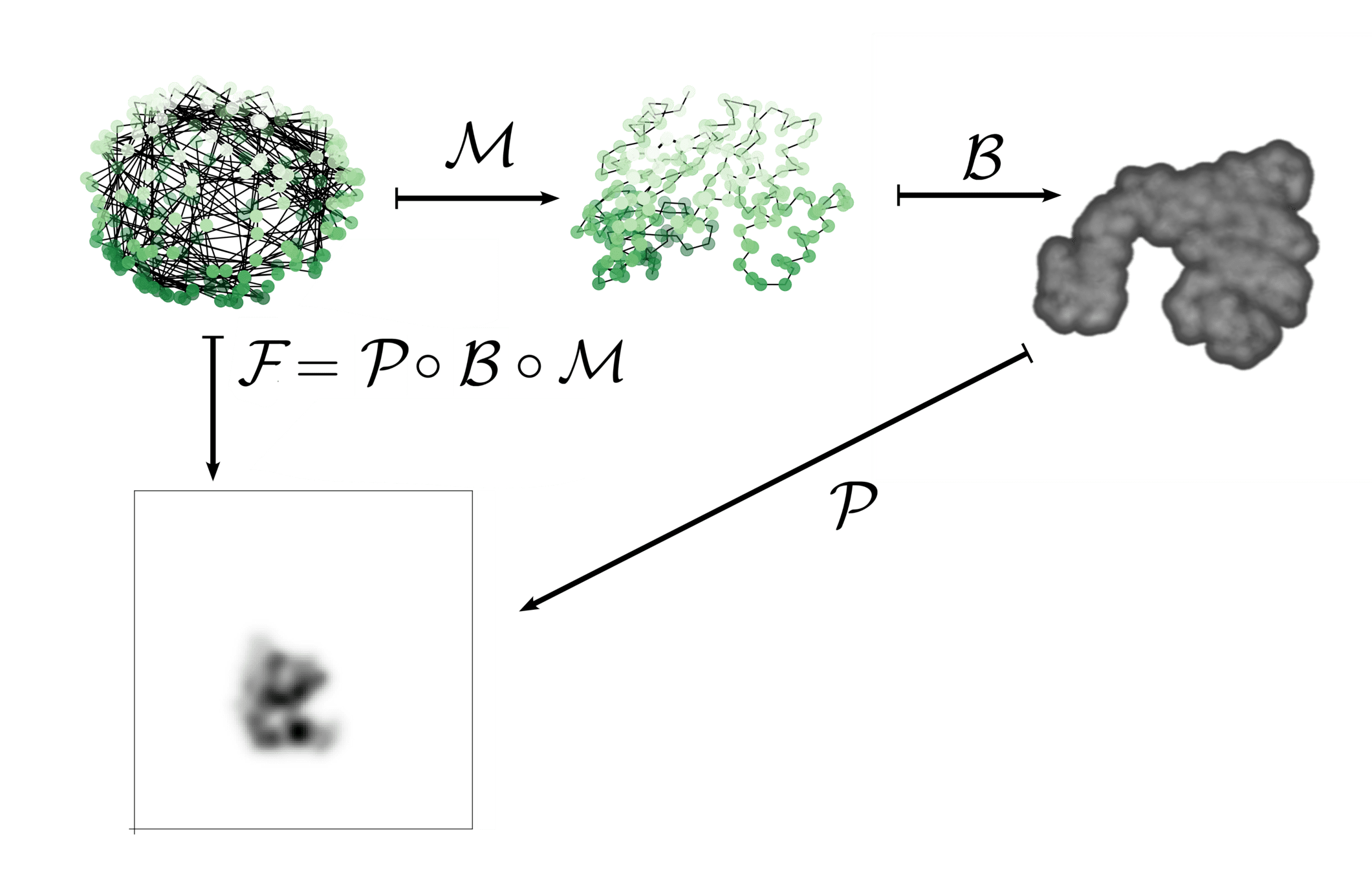
Include a forward operator \(\mathcal{F}\colon V \to W\)

\underbrace{d_W^2(\mathcal{F}(\gamma(1).A),B)}_{\text{Matching energy \\changes}}+\underbrace{\int_0^1 \langle \nu(t),\nu(t) \rangle_e \mathrm{d}t}_{\text{Regularization is the same}}

Initial shape: \(A \in V\), target shape: \(B \in W\)

"Reconstructs" the \(\gamma(1).A\) that best would map to \(B\)

Research questions and approaches

Paper IV

Paper VI

Constrain landmarks to move only in certain directions

The reconstruction of protein confirmations is difficult.

Applications cases of (indirect) shape matching

Shapes are landmarks
Deformation group is diffeomorphism group
Possible indirect matching against labels

Shapes are protein backbones
Deformation group is a matrix group
Indirect matching against noisy cryo-EM images

Main scientific question:

Can constrained landmark matching be seen as a neural net?

Main scientific question:

Is indirect shape matching a viable approach for protein conformation reconstruction?

Structure-preserving numerics for geometric mechanics

Paper III and VII research questions

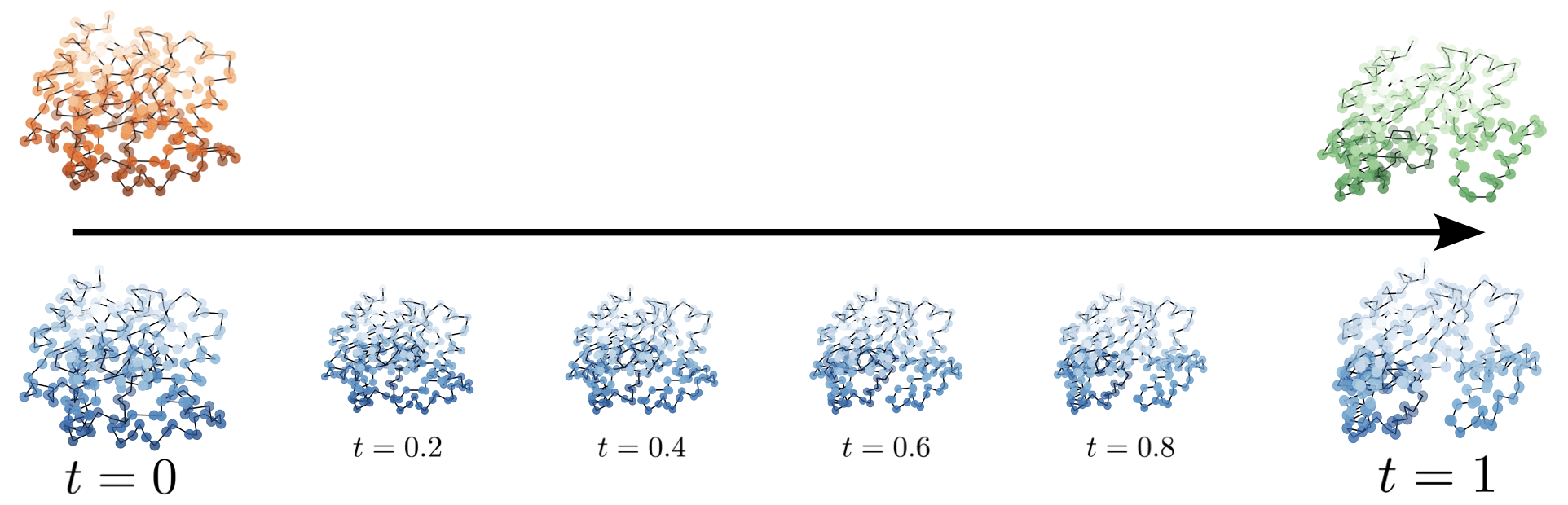
Mechanical problems

Focus here: Lie–Poisson systems: Related to the evolution of observables in Hamiltonian mechanics

Evolves on dual of Lie algebra \(\mathfrak{g}^*\)

\,\dot X_t = \operatorname{ad}^*_{\delta H(X_t)} X_t\,

Complexified Euler equations:

\mathfrak{g}^* = C^\infty_0(\mathbb S^2; \mathbb C)\\ \dot \omega = \{\bar{\psi},\omega\}_{\mathbb{C}}

Rigid body equations:

\mathfrak{g}^* = \mathfrak{so}(3)^*\\ \dot{m} = m \times I^{-1} m

Geometry of LP systems

\,\dot X_t = \operatorname{ad}^*_{\delta H(X_t)} X_t\,

LP system has a rigid geometric structure:

they evolve on coadjoint orbits

In addition: conserved quantites

They look like onions, sometimes

Discretizations in time for ODEs and time and space for PDEs with LP structure should respect LP structure and conserved quantities

Research questions and approaches

Paper III

Paper VII

Stochastic Lie–Poisson systems in high but finite dimensions
Existing geometric integrators can be expensive if dimension is large
Deterministic case: IsoMP method
Can we develop a stochastic IsoMP method?

Main scientific question: Development, analysis and convergence of method

Complexified Euler equations on \(\mathbb T^2\) are ill-posed (blow-up)
Zeitlin's method + IsoMP provides an LP-preserving numerical method
Blow-up is inherently at limit of numerics, what is a reliable signature?

Main scientific question: How to detect blow-up with geometric numerics?

Scientific questions: recap

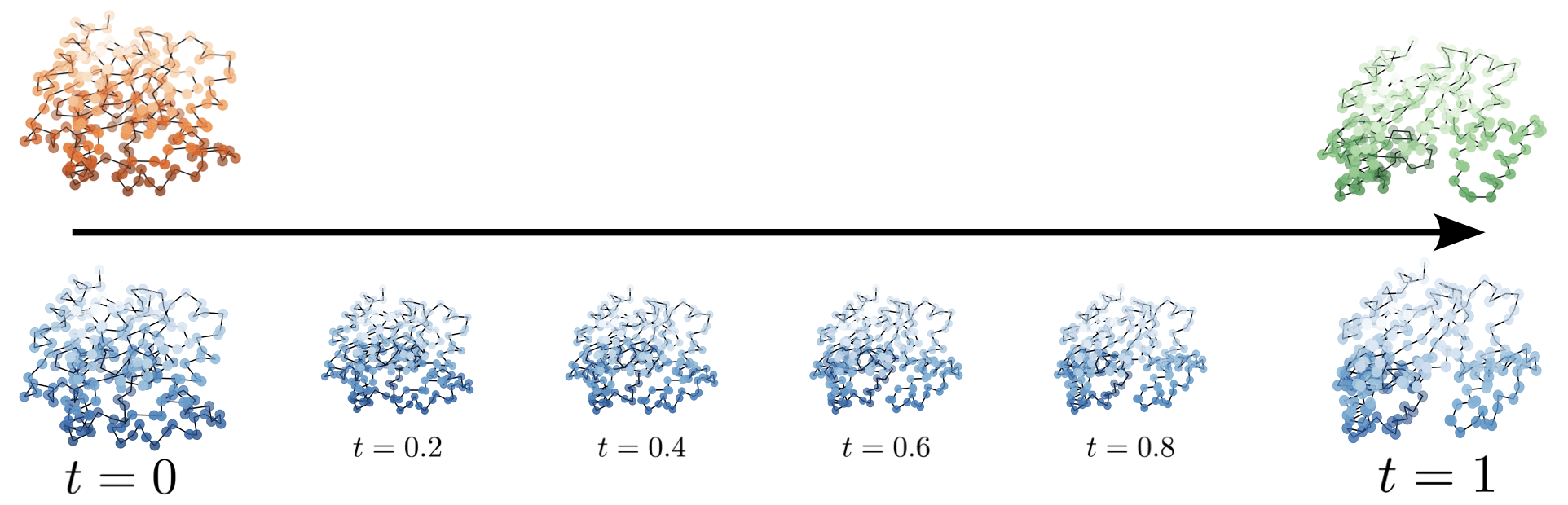
What is convergence behavior analysis of our methods for SFEM-based simulation approach of random fields?

What is the behavior of our stochastic IsoMP method?
What is a reliable numerical signature of blow-up?

What is the connection between constrained landmark matching and neural networks?
Does shape analysis have a future in protein imaging?

Thesis research

Paper I: Generate random fields of well-known type on the sphere by SPDE and SFEM approach.

Paper II: Generate random fields of new type by coloring approximated white noise

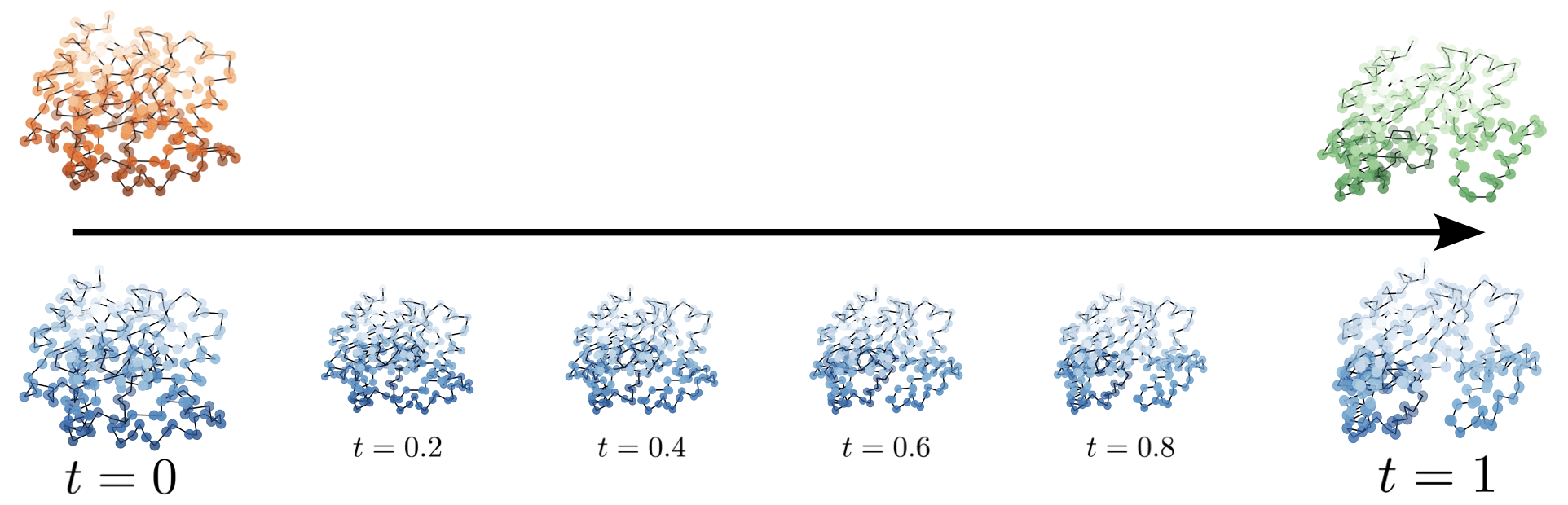
Paper III: Development of structure-preserving integration of stochastic Lie–Poisson systems

Paper VII: Trustworthy structure preserving numerics for blow-up detection

Paper IV: Sub–Riemannian landmark matching and connections to neural networks

Paper V: Convergence analysis of a gradient flow

Paper VI: Indirect shape matching for protein conformation reconstruction

Thesis research

Paper I: Generate random fields of well-known type on the sphere by SPDE and SFEM approach.

Paper II: Generate random fields of new type by coloring approximated white noise

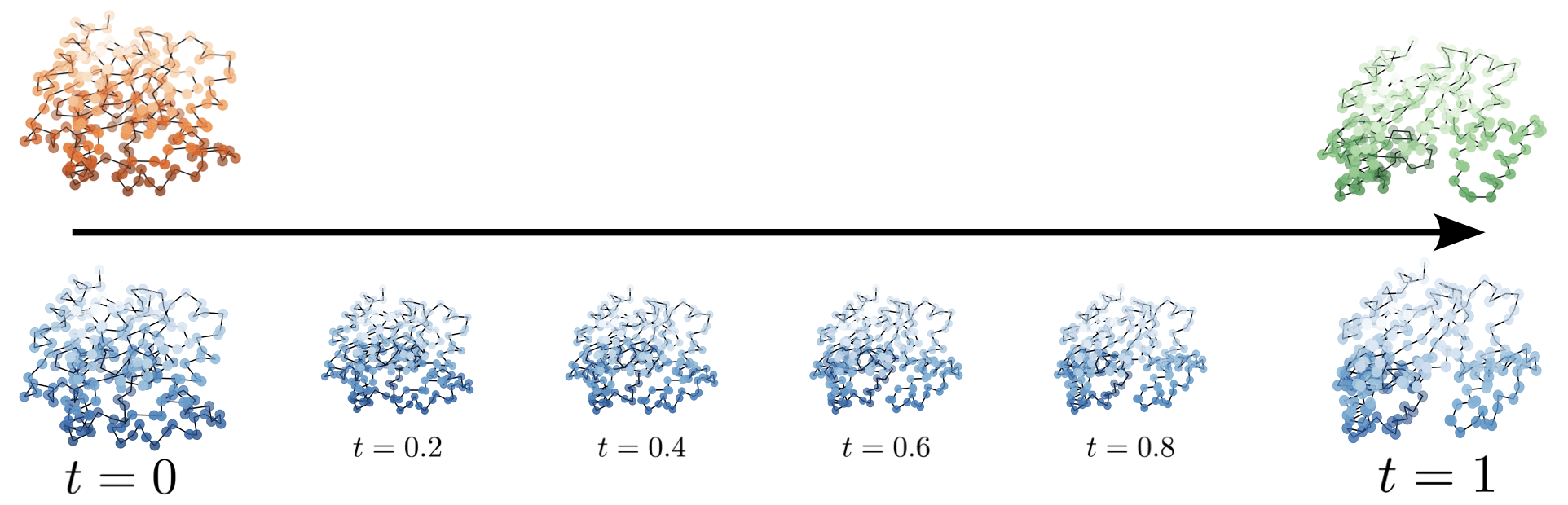
Paper IV: Sub–Riemannian landmark matching and connections to neural networks

Paper V: Convergence analysis of a gradient flow

Paper VI: Indirect shape matching for protein conformation reconstruction

Paper III: Development of structure-preserving integration of stochastic Lie–Poisson systems

Paper VII: Trustworthy structure preserving numerics for blow-up detection

Main findings

Paper II: Strong error rates for the algorithms proven using functional calculus approach

Paper III: IsoMP is made stochastic. Method is analyzed by using the geometric structure of LP systems.

Paper VI: Shape matching is adapted to the protein conformation reconstruction setting and is showcased as a promising approach

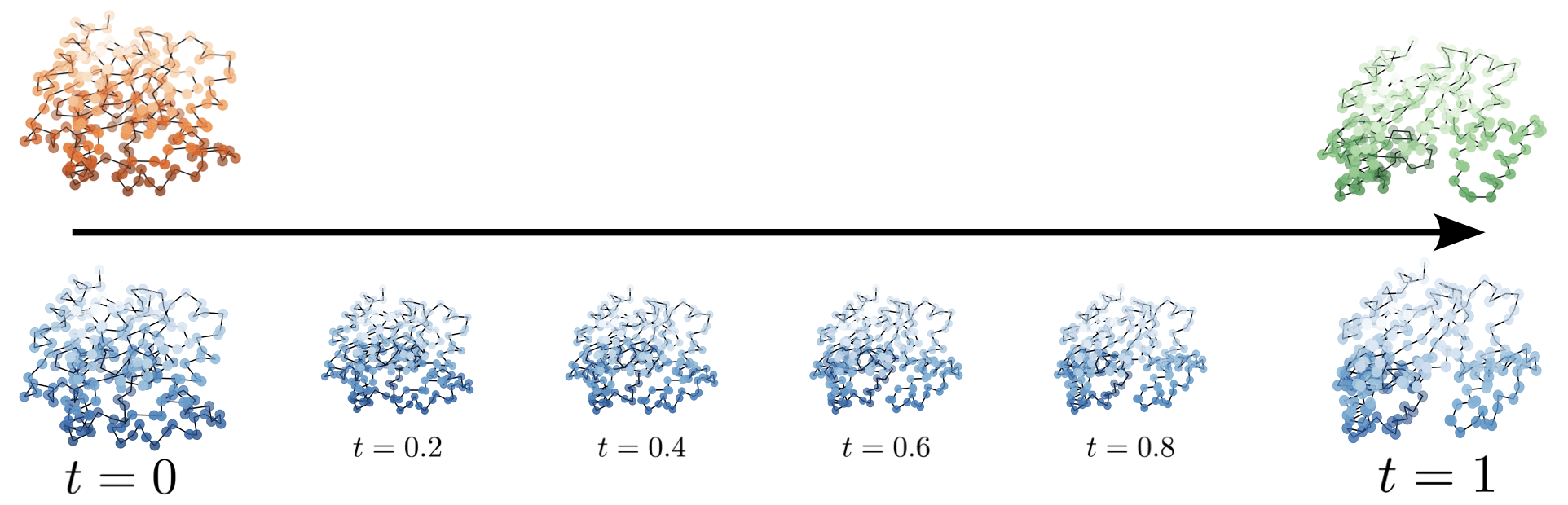
Random fields via stochastic partial differential equations

Paper II results

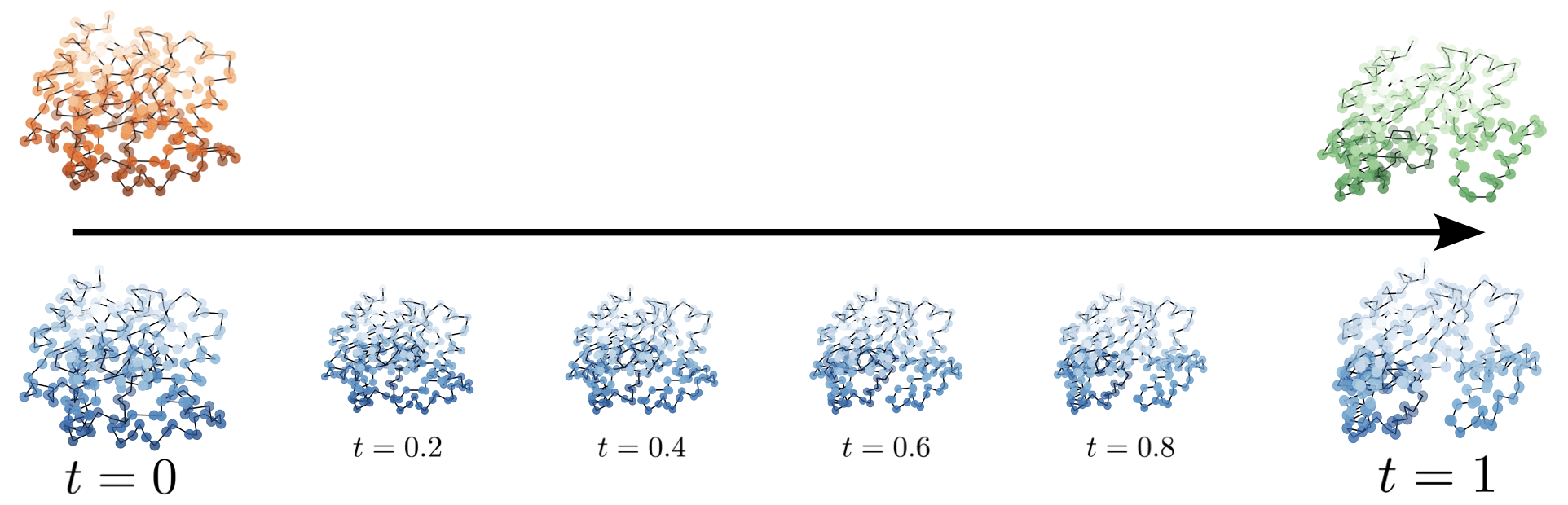
Some more details on paper II

~\mathcal{Z} = \zeta(\mathcal L)\mathcal W = \sum_{i=1}^\infty \zeta(\lambda_i) W_i e_i~

\mathcal{W} = \sum_{i=1}^\infty W_i e_i, W_i \sim \mathsf N(0,1)

Our approach is best understood by spectral expansions.

Eigenpairs of \( \mathcal{L} \): \((\lambda_i,e_i)\)

\mathsf Z_h = \zeta(\mathsf L_h) \mathsf W_h= \sum_{i=1}^{N_h} \zeta(\Lambda_{i,h})\overline{W}_i E_{i,h}

Field approximation using eigenpairs \((\Lambda_{i,h},E_{i,h})\) of \(\mathsf L_h\)

Geometry

approximation

Our method

In practice:

\zeta(\mathsf L_h) \mathsf W_h = \sum_{i=1}^{N_h} Z_i \psi_i

Key benefit:

Find a mesh and you can simulate GRFs on it! No need to know the geodesic distance

Research question: Strong error?

\((Z_i)\) are Gaussian with covariance matrix determined by \(\zeta\) and FEM matrices

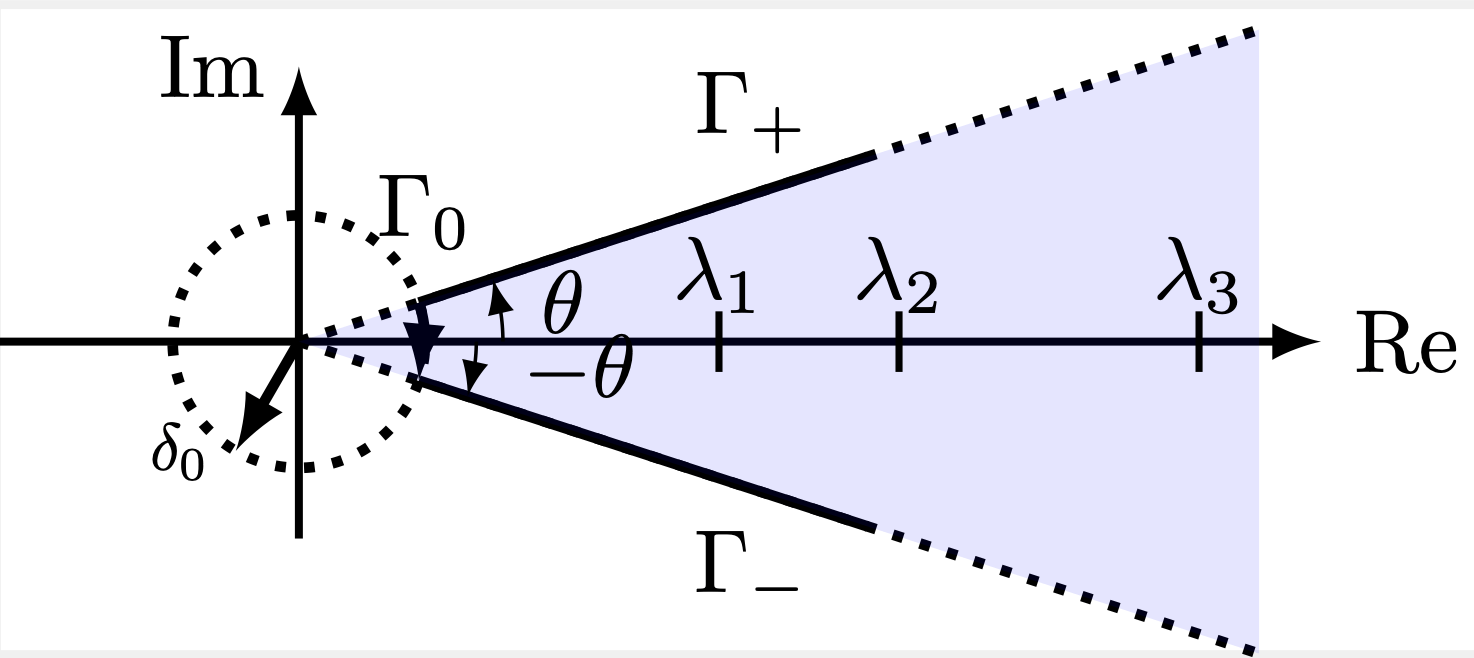
Resolving research question

\|\mathcal Z - \mathsf Z_h^\ell\|_{L^2} \lesssim K_\alpha(h) h^{\min\{\alpha -d/4; 2\}} \\ K_\alpha(h) = \begin{cases} |\log h| ~\text{ if } d/4< \alpha \leq 1 \\ |\log h|^{3/2} \text{ if } 1 < \alpha <1+d/2 \\ |\log h|^{1/2} if \alpha \geq 1+d/2 \text{ else }\end{cases}

Key method:

\zeta(\mathcal L) f = \frac{1}{2\pi i } \int_{\Gamma} \zeta(z)(z-\mathcal{L})^{-1}f

Shape analysis

and matching problems

Paper VI results

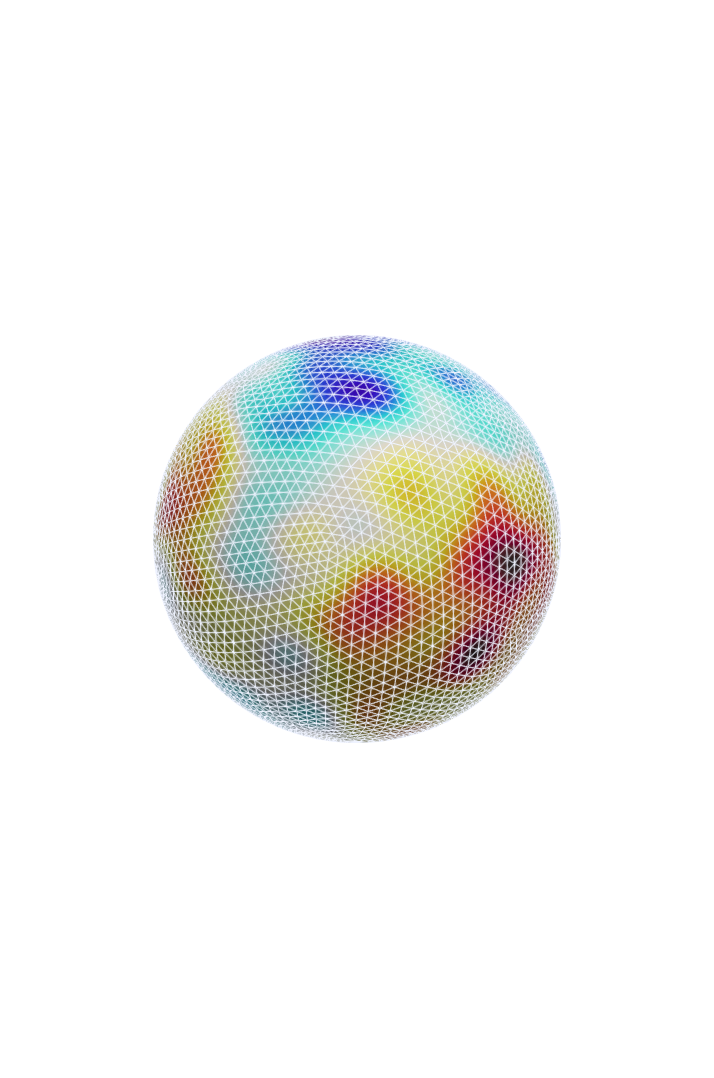
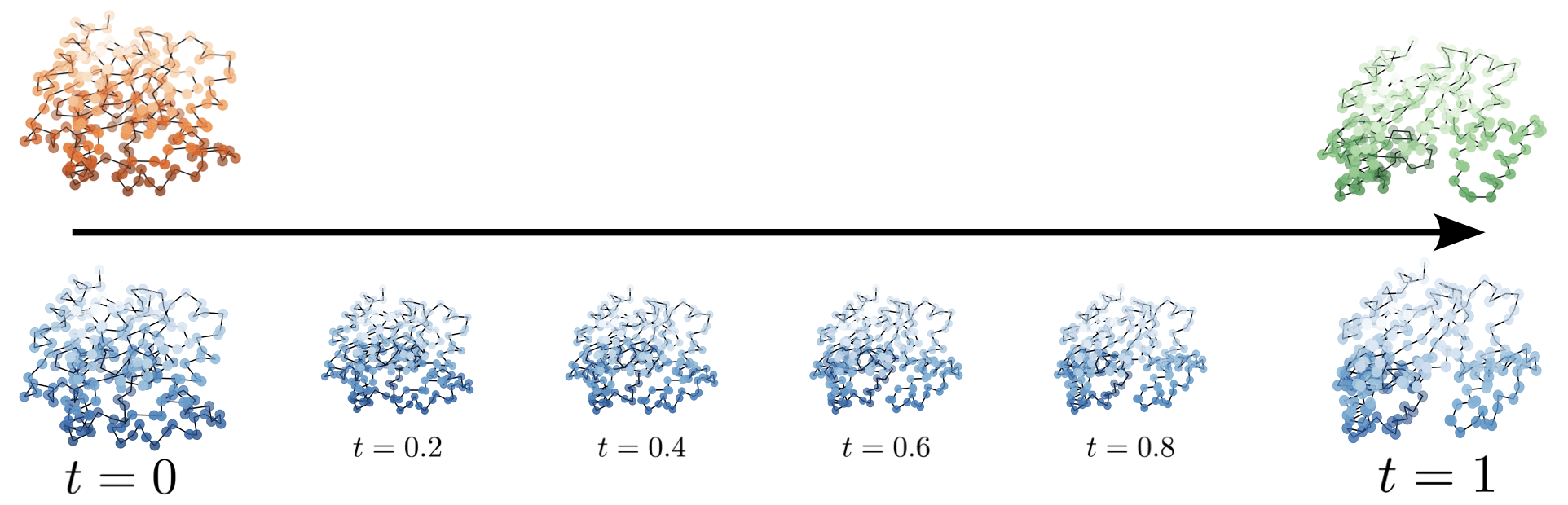
Cryo-EM

in 30 seconds (by a maths person)

Electron

microscope

Low dose - low SnR

Many images

Many copies of the same protein but at different orientations and conformations

Proteins in 30 seconds (by a mathematician)

In this work: forget about everything but the \(C_\alpha\)s

Relative positions

\((\mathbb R^3)^N\)

Mathematical model for proteins

Proteins: mathematical model

Idea: Take a known conformation of the protein as a "prior"

Deform it until it matches target

How to deform? And what energy to use?

Optimization problem!

Shape for Cryo-EM

Shape space: space of relative positions \(V = \mathbb{R}^{3N}\)

Data space - 2D images, \(L^2(\mathbb{R}^2)\) (very noisy!)

We want rigid deformations, so \(G = \operatorname{SO}(3)^N\)

Forward model

Shape for Cryo-EM

\mathcal E(\nu) = \frac{1}{2} \sum_{i \in 1}^N\left\| \mathcal{F}_i(\Phi(\gamma(1),w)) - y_i \right\|^2_{L^2(\mathbb R^2)} + \lambda \int_0^1 \operatorname{Tr}(\nu^TL\nu)\\ \dot \gamma = \nu \gamma, \gamma(0) = e

Minimization of \(\mathcal E(\nu) \) reduces to:

\dot m = \operatorname{ad}^*_v m, m = \mathbb I \nu \\ \dot \gamma = \nu \gamma, \gamma(0) = e

+ shooting

Shape for Cryo-EM

Guess \(\nu(0)\) (or path sampled at discrete points)
- Integrate to get \(\gamma(1)\)
- Evaluate \(\mathcal{E}\) and compute \(\nabla_{\nu(0)} \mathcal{E}\)
Update \(\nu(0)\) with favorite algorithm (A few GD steps and then L-BFGS-B)

Gradient is available (even easy to compute)

Shape for Cryo-EM

\dot m = \operatorname{ad}^*_v m, m = \mathbb I \nu \\ \dot \gamma = \nu \gamma, \gamma(0) = e

Deformation

What we want

What we see

Where we start

Research question: It's looking viable

Results using shape framework

Structure-preserving numerics for geometric mechanics

Paper III results

\(M\) independent scalar Brownian motions \(W^1, \ldots, W^M\)
\(M\) noise Hamiltonians \(H_k\colon\mathfrak{g}^*\to \R\)

~ \mathrm d X_t =\operatorname{ad}^*_{\delta H_0(X_t)} X_t \, \mathrm d t + \sum_{k=1}^M \operatorname{ad}^*_{\delta H_k(X_t)} X_t \circ \mathrm d W_t^k ~

Stochastic LP systems

LP systems on \(\mathfrak{g}^*\), stochastic or not, are reductions of Hamiltonian systems on \(T^*G \cong G \times \mathfrak{g}^*\)

There is a mapping \(\mu\) that takes LP system to a left-invariant Hamiltonian system (reconstruction)

Stochastic LP systems

upstairs

downstairs

Stochastic Hamiltonian system:

know how to numerically integrate.

Properties of method known

Stochastic Lie–Poisson system:

Don't know how to integrate

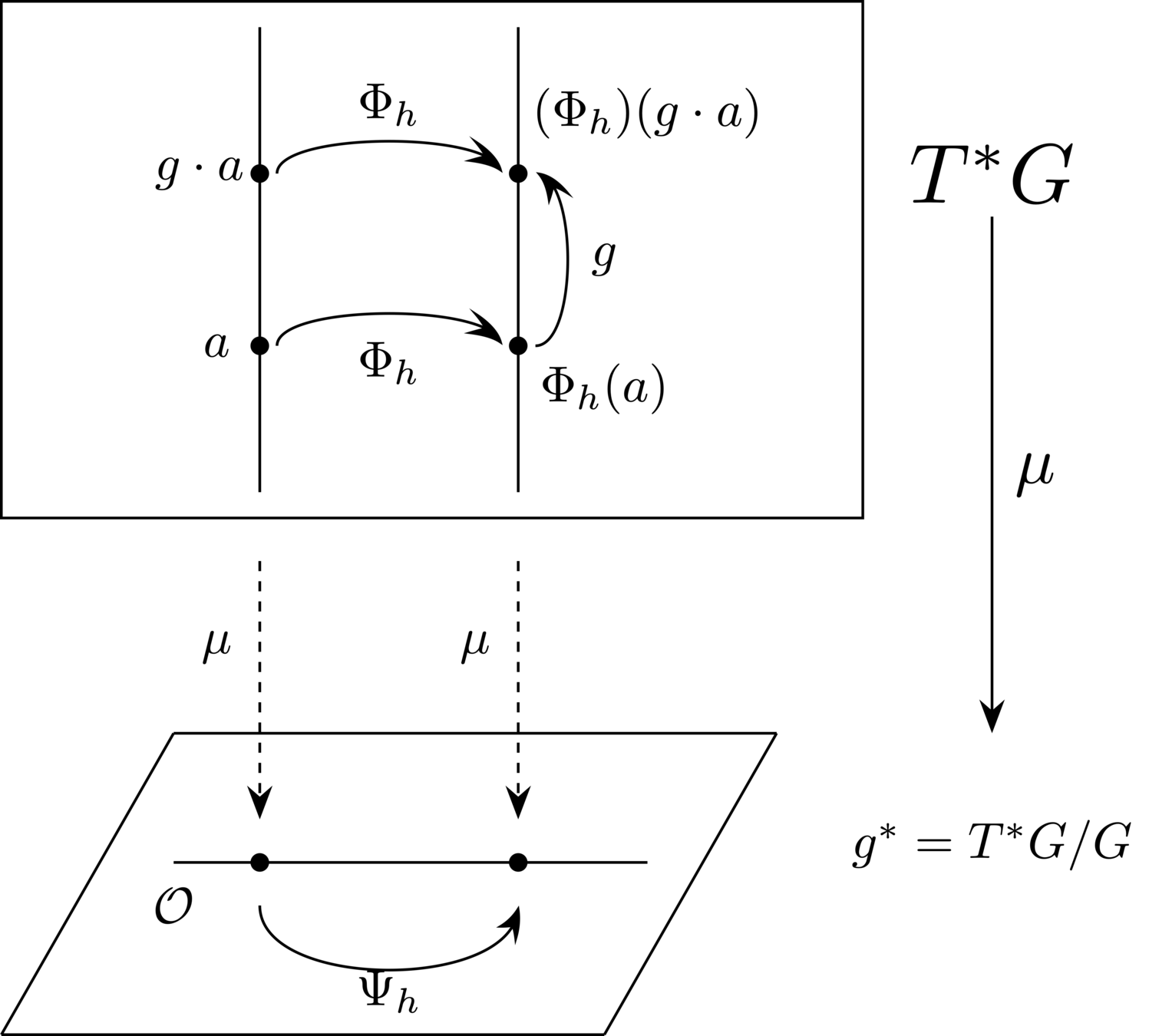
Idea: make sure the "stairs" \(\mu\) has nice properties and takes integrator upstairs to integrator downstairs

Intuitive picture:

\(\Phi_h \colon T^*G \to T^* G\): \(G\)-equivariant symplectic integrator \(\rightarrow\)
Reduces to a Lie–Poisson integrator by \(\mu\)

Use Implicit midpoint

Integration without tears

Exploit the reconstruction!

\begin{split} \mathrm d Q_t &= Q_t\nabla H_0(\mu(Q_t,P_t)) \, \mathrm d t + \sum_{i=1}^M Q_t \nabla H_i (\mu(Q_t,P_t))\circ \mathrm d W_t^i, \\ \mathrm d P_t &= -P_t\nabla H_0(\mu(Q_t,P_t))^* \, \mathrm d t - \sum_{i=1}^M P_t \nabla H_i (\mu(Q_t,P_t))^* \circ \mathrm d W_t^i. \end{split}

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~

\mathfrak{g}^*

Error analysis without tears

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~

Check the literature for error analysis for implicit midpoint

Exploit the reconstruction!

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~

\mathfrak{g}^*

Result

~\sup_{0 \leq n \leq N} \mathbb E\left[ \|X(hn)-X_n\|^2\right]^{1/2} \leq \kappa h^{1/2}\\ \sup_{0 \leq n \leq N} \left|\mathbb E[\phi(X(hn))-\phi(X_n)]\right| \leq \kappa h~

Method is Lie–Poisson (preserves LP structure) surely

Scientific question is resolved

\begin{split} \tilde{\Psi}_{h, n}(\tilde{X}) &= \nabla H_0(\tilde{X})^*h + \sum_{i=1}^M\nabla H_i(\tilde{X})^*(\zeta_i)_n\sqrt{h}, \\ X_n &= \left(I- \frac{1}{2}\tilde{\Psi}_{h, n}(\tilde{X})\right) \tilde{X} \left(I+\frac{1}{2}\tilde{\Psi}_{h, n}(\tilde{X})\right), \\ X_{n+1} &= \left(I+\frac{1}{2}\tilde{\Psi}_{h, n}(\tilde{X})\right) \tilde{X} \left(I- \frac{1}{2}\tilde{\Psi}_{h, n}(\tilde{X})\right). \end{split}

Scientific questions: conclusion

What is convergence behavior analysis of our methods for SFEM-based simulation approach of random fields? Resolved in paper I and II

What is the behavior of the stochastic IsoMP method? Resolved in paper III
What is a reliable numerical signature of blow-up? Suggestion in paper VII

What is the connection between constrained landmark matching and neural networks? One possible connection is studied in paper IV
Does shape analysis have a future in protein imaging? Results in paper VI suggests it.

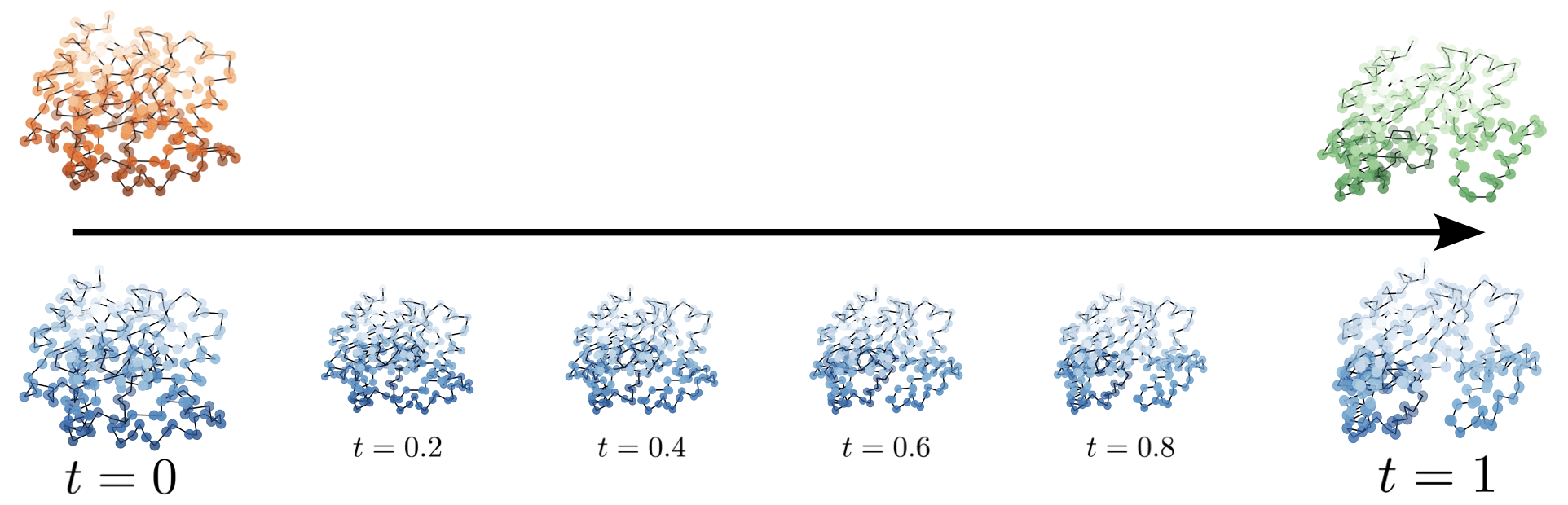
Outlook (if I had one more year)

Idea I: Extend to spatio-temporal fields

Idea II: Compute weak errors

Idea III: Stationarity on general manifolds

Idea IV: Regularization by noise in structure-preserving simulations

Idea V: Blow-up for axisymmetric 3D Euler with Zeitlin

Idea VI: GNNs for better fidelity terms in protein matching for more realistic behavior

Idea VII: Side chain inclusion

Idea VIII: Indirect shape matching via gradient flows

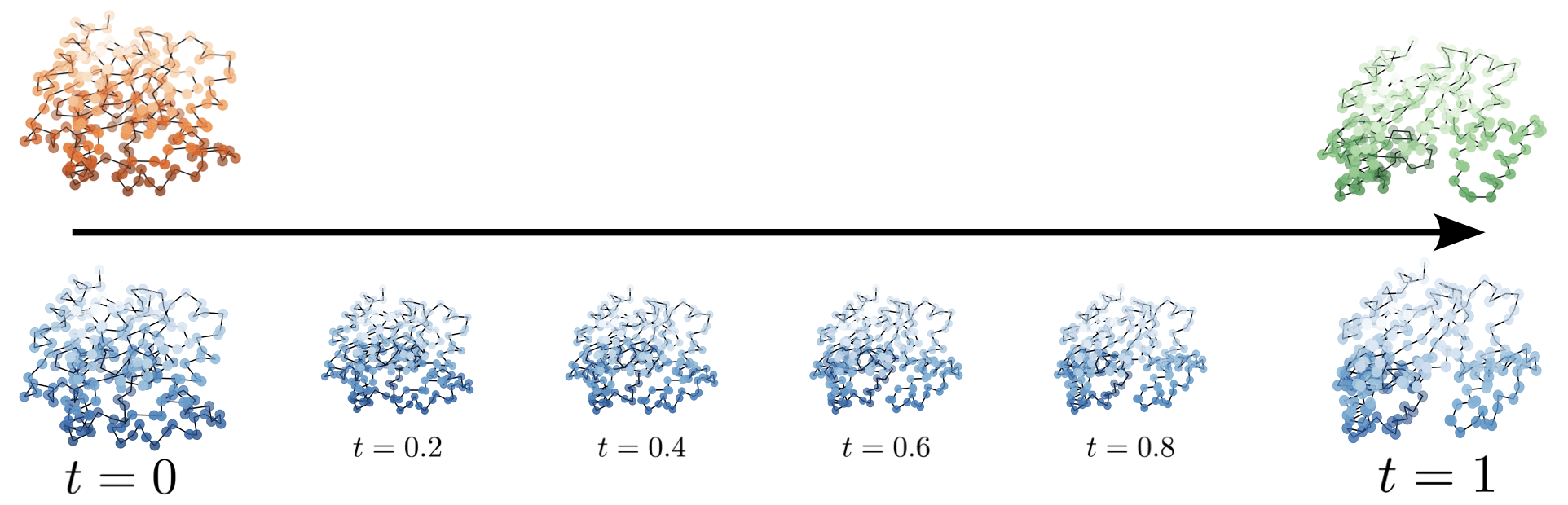
Paper I: Surface finite element approximation of spherical Whittle-Matérn Gaussian random fields. With Annika Lang and Mihály Kovács

Paper II: Non-stationary Gaussian random fields on hypersurfaces: Sampling and strong error analysis. With Annika Lang and Mike Pereira

Thesis research: coauthors

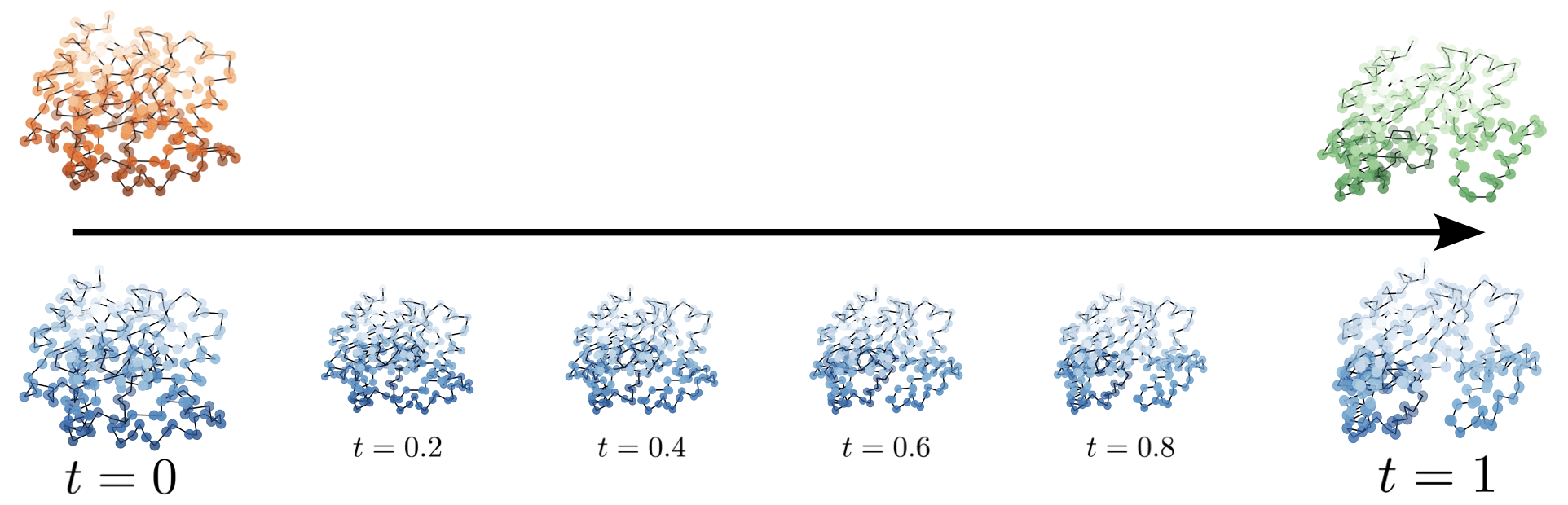
Paper III: An exponential map free implicit midpoint method for stochastic Lie-Poisson systems. Joint with Annika Lang, Sagy Ephrati and Erwin Luesink

Paper VII: On spectral scaling laws for averaged turbulence on the sphere. Joint with Klas Modin

Paper IV: Sub-Riemannian landmark matching and its interpretation as residual neural networks. With Klas Modin

Paper V: Convergence of the vertical gradient flow for the Gaussian Monge problem. With Klas Modin

Paper VI: Geometric shape matching for recovering protein conformations from single-particle Cryo-EM data. With Ozan Öktem, Jonathan Krook and Klas Modin

Extra slides: Paper I

Details of methods and proof

Error

EXTRA: Special case: sphere

Main difference: the fractional part is approximated by a Dunford–Taylor integral sinc quadrature!

(\kappa^2-\Delta_{\mathbb S^2})^{\beta} u = \mathcal{W}

\mathcal{L} u^1=F

\mathcal{L} u^2=u^1

\mathcal{L} u^3=u^2

\vdots

\mathcal{L}^{\{\beta\}} u=u^{\left \lfloor{\beta}\right \rfloor }

Split problems to obtain recursion!

\(\|u-u_{Q,k}\|\) decays exponentially in \(k\)

\mathcal{L}^{-\{\beta\}} =\frac{\sin( \pi \{\beta\})}{\pi}\int_{-\infty}^{\infty} e^{2 \{\beta\} y} \left( I+e^{2y}\mathcal{L}\right)^{-1} \, \mathrm{d} y\\

\mathcal{L}^{-\{\beta\}} \approx Q^{\{\beta\}}_k= \frac{2 k \sin(\pi \{\beta\})}{\pi} \sum_{l=-\color{ForestGreen}{K^{-}}}^{\color{ForestGreen}{K^+}} e^{2\{\beta\} y_{l}} \color{forestgreen}{\left(I+e^{2 y_l}\mathcal{L}\right)^{-1}} \\

\color{black}{u \approx u_{Q,k}= Q^{\{\beta\}}_k \color{ForestGreen}u^{\lfloor\beta \rfloor}}

EXTRA: Special case: sphere

\|u-u_{h}^\ell\| \leq C \left( h^2 \|F\|{+}{\color{ForestGreen}{\|F-F_h^\ell\|}}\right)

In general

\color{ForestGreen}{\|u^{\lfloor \beta \rfloor }{-}u_{h}^{\lfloor \beta \rfloor ,\ell}\|} \color{black}{{\leq} C\left(h^2 \|u_L^{\lfloor \beta \rfloor -1}\|{+}\|u_L^{\lfloor \beta \rfloor -1}{-}u_{L,h}^{\lfloor \beta \rfloor-1 ,\ell}\|\right)}

The error from the geometry discretization is the error of the previous problem in the recursion!

\|u_{l}{-}u_{h,l}^\ell\| {\leq} C \left(h^2 \|u^{\lfloor \beta \rfloor }\| {+}{\color{ForestGreen}{\|u^{\lfloor \beta \rfloor }{-}u_{h}^{\lfloor \beta \rfloor ,\ell}\|}}\right)

EXTRA: Special case: sphere

\mathcal{W}\sim \sum_{l=1}^\infty\sum_{m=-l}^l a_{l,m}Y_{l,m}

\mathcal{W}_L= \sum_{l=1}^L\sum_{m=-l}^l a_{l,m}Y_{l,m}

\|u-u_L\|_* \leq C_{\kappa}\left(\frac{1}{2\beta-1}+\frac{1}{4\beta-1}\right)L^{1-2\beta}

~\\ \|u-u_{L,h}^{\ell}\|_* \leq C(L+1)\left({L^{-2\beta}}{+e^{-\pi^2/(4k)}+ h^s(L+1)^{s}}\right)\\ ~

EXTRA: Special case: sphere

Extra slides: stationarity of RFs on surfaces

G-homogeneous spaces

G-iostropic fields

Geodesic stationarity

Counterexample

EXTRA: Stationarity/isotropic

\(G\) is a Lie group. Let \(M\) be a G-homogeneous space.

\(G\) acts transitively on \(M\):

For all \(x,y \in M\) there is a \(g \in G\) so that \(g\cdot x = y \)

Examples:

\(\operatorname{SE}(d)\) and \(\mathbb{R}^d\)
\(\operatorname{SO}(d)\) and \(\mathbb{S}^d\)
Orthogonal group and Stiefel manifold

Stationarity = probabilistic invariance under action of group.

Consequence: covariance function depends only on geodesic distance, mean function is constant

EXTRA: Stationarity/isotropic

Hints at a definition of "geodesic stationarity"

A field is geodesically stationary if its mean function is constant and its covariance functions depends only on the geodesic distance

However- seems to not work!

EXTRA: Stationarity/isotropic

Feeling: even on a manifold \((M,g)\) that has trivial isometry group, a field generated by \(\mathcal Z = \zeta(\Delta_M) \mathcal W\)

However: covariance function

C(x,y) = \sum_{i=1}^\infty \zeta^2(\lambda_i) e_i(x) e_i(y)

Insert \(\zeta = \exp(-\Delta_M/2)\)

C(x,y) = \sum_{i=1}^\infty e^{-\lambda_i} e_i(x) e_i(y)

EXTRA: Stationarity/isotropic

C(x,y) = \sum_{i=1}^\infty e^{-\lambda_i} e_i(x) e_i(y)

Heat kernel!

In other words: No hope of only dependence on geodesic distance.

However: asymptotic expansions exist for kernels. There might be some hope to consider only very local expansions to hopefully obtain expressions for the "local covariance function" => maybe the correct notion is one of "local stationarity"?

EXTRA: A fun conclusion

Well-studied object in Euclidean case.

First step for generalization is not to go to manifolds directly, but to homogenous spaces

(an actual thesis in the strict etymological sense of the word)

Extra slides: surface finite elements

Main computational tool: FEM

On Euclidean spaces

Just triangulate the domain!

\mathcal{D}

Put the pieces back together, get the original domain!

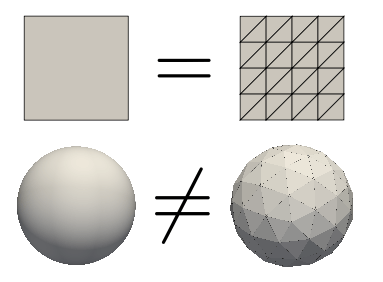
Main computational tool: FEM

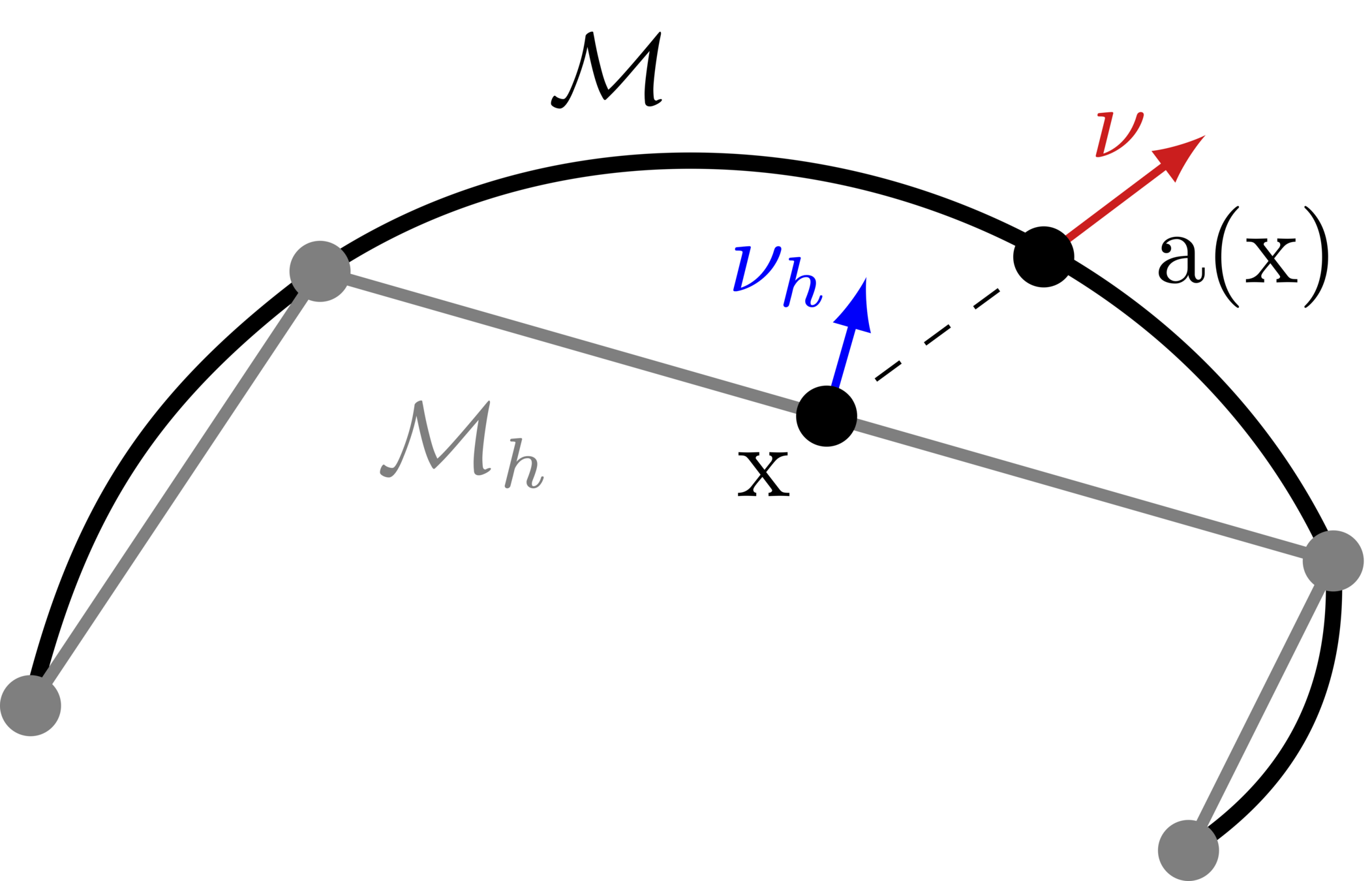
On manifolds!

Step 1: Triangulate the domain

\mathcal{M}

\mathcal{M}_h

Issue: Approximate solutions live on \(\mathcal{M}_h\), not \(\mathcal{M}\)!

Put the pieces back together, don't get the same domain!

Step 2: FEM space \(S_h \subset H^1(\mathcal{M}_h)\) of p.w., continuous, linear functions

Main computational tool: FEM

On manifolds!

Step 1: Triangulate the domain

\mathcal{M}

\mathcal{M}_h

Issue: Approximate solutions live on \(\mathcal{M}_h\), not \(\mathcal{M}\)!

Put the pieces back together, don't get the same domain!

Step 2: FEM space \(S_h \subset H^1(\mathcal{M}_h)\) of p.w., continuous, linear functions

\mathcal{M}_h

Given \(\eta: \mathcal{M}_h \to \mathbb{R}\), \(\eta^\ell= \eta \circ a\) is on \(\mathcal{M}\)!

Step 3: Key tool in surface finite elements: the lift

Takeway: FEM error similar to flat case, up to a "geometry error" term

Main computational tool: FEM

Extra slides: some notes on kernel functions

Euclidean domains

To simulate, specify mean and covariance

\mu(x) = 0 \\ C(x,y) = \sigma^2\frac{2^{1-\nu}}{\Gamma(\nu)}{\Bigg(\sqrt{2\nu}\frac{d(x,y)}{\rho}\Bigg)}^\nu K_\nu\Bigg(\sqrt{2\nu}\frac{d(x,y)}{\rho}\Bigg)

Matérn covariance kernel
Flexible, used a lot.
Depends solely on the distance between \(x\) and \(y\).
Due to stationarity/isotropy.

The sampling question: resolved in isotropic, Euclidean case since the beginning

Euclidean domains

To simulate, specify mean and covariance

\mu(x) = 0 \\ C(x,y) = \sigma^2\frac{2^{1-\nu}}{\Gamma(\nu)}{\Bigg(\sqrt{2\nu}\frac{d(x,y)}{\rho}\Bigg)}^\nu K_\nu\Bigg(\sqrt{2\nu}\frac{d(x,y)}{\rho}\Bigg)

Matérn covariance kernel
Flexible, used a lot.
Depends solely on the distance between \(x\) and \(y\).
Due to stationarity/isotropy.

The sampling question: resolved in isotropic, Euclidean case since the beginning

Curved spaces?

Idea: replace \(d(x,y)\) with \(d_M(x,y)\) in the Matérn kernel
Problem: doesn't always work (Gneitling, 2013)
Solution: Hand-craft covariance functions?

(Whittle, 1953) Other, more geometric idea: Matérn field on \(\R^d\) solves:

(\kappa^2-\Delta)^\beta \mathcal Z = \mathcal W

Write down equivalent SPDE on manifold

Curved spaces?

(\kappa^2-\Delta_{M})^\beta \mathcal Z = \mathcal W

The Laplace–Beltrami operator is a geometric object, so this works for all manifolds

(terms and conditions apply)

Sampling by solving the PDE approximately (numerics has entered!)

Extra slides: paper II

Concrete examples

The operator + model details

The FEM operators

Why not compute e.f.s

Actual matrices used

Details on the

EXTRA: Concrete example I

\mathcal M = \mathbb{S}^2, \gamma(\lambda) = \lambda^{-\alpha}, \alpha > 1/2

D_{ij} = \delta_{ij}

V(x) = 10

\alpha = 0.55

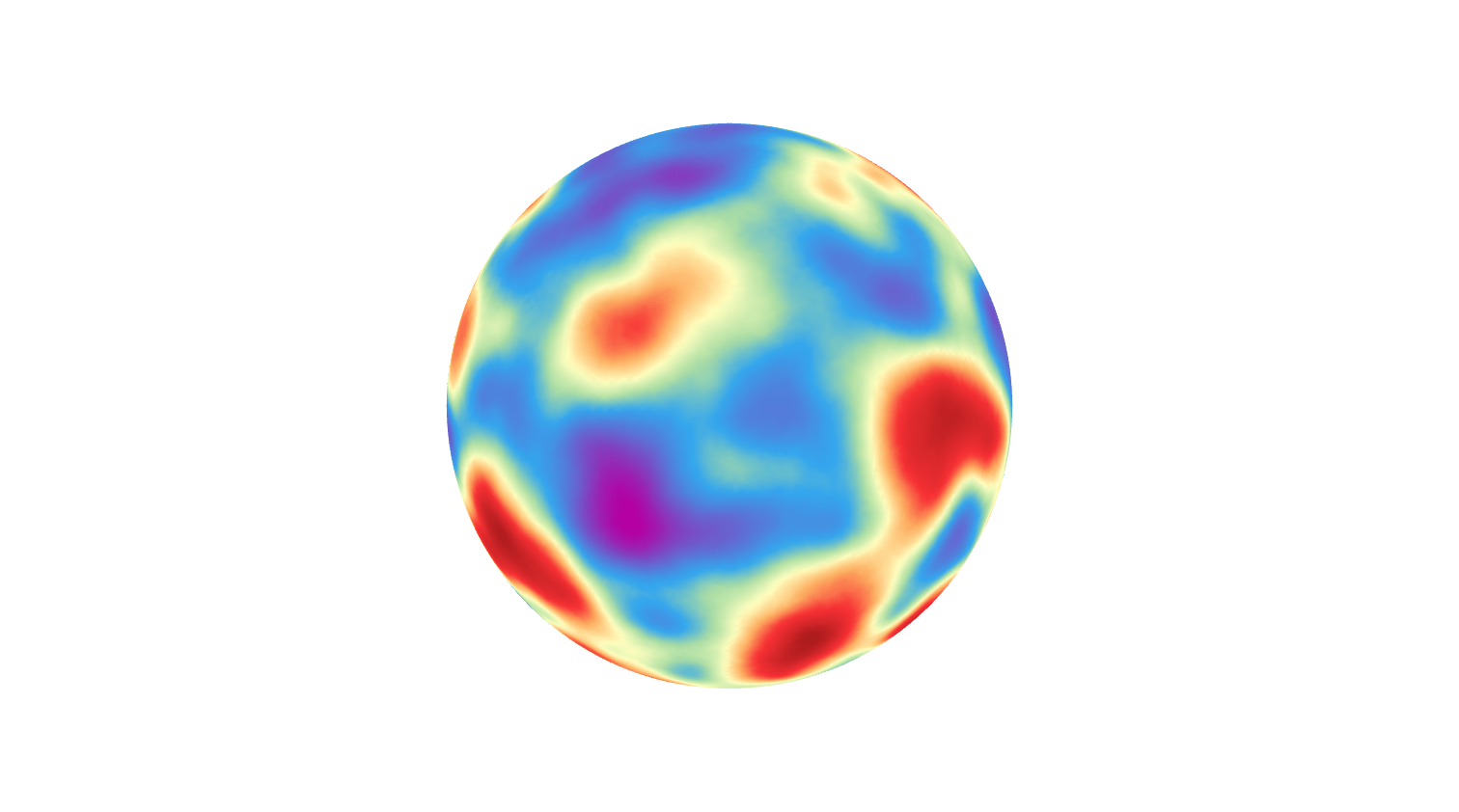
(Whittle-) Matérn random fields given by SPDE \((\kappa^2-\Delta_{\mathbb{S}^2})^\beta \mathcal Z = \mathcal{W}\)!

EXTRA: Concrete example II

\mathcal M = \mathbb{S}^2, \gamma(\lambda) = \lambda^{-0.75}

D_{ij} = \delta_{ij}

V(x) = \begin{cases} 10^5 \quad \text{if } x_2^6+x_1^3-x_3^2 \in (0.1,0.5)\\ 10 \quad \text{else} \end{cases}

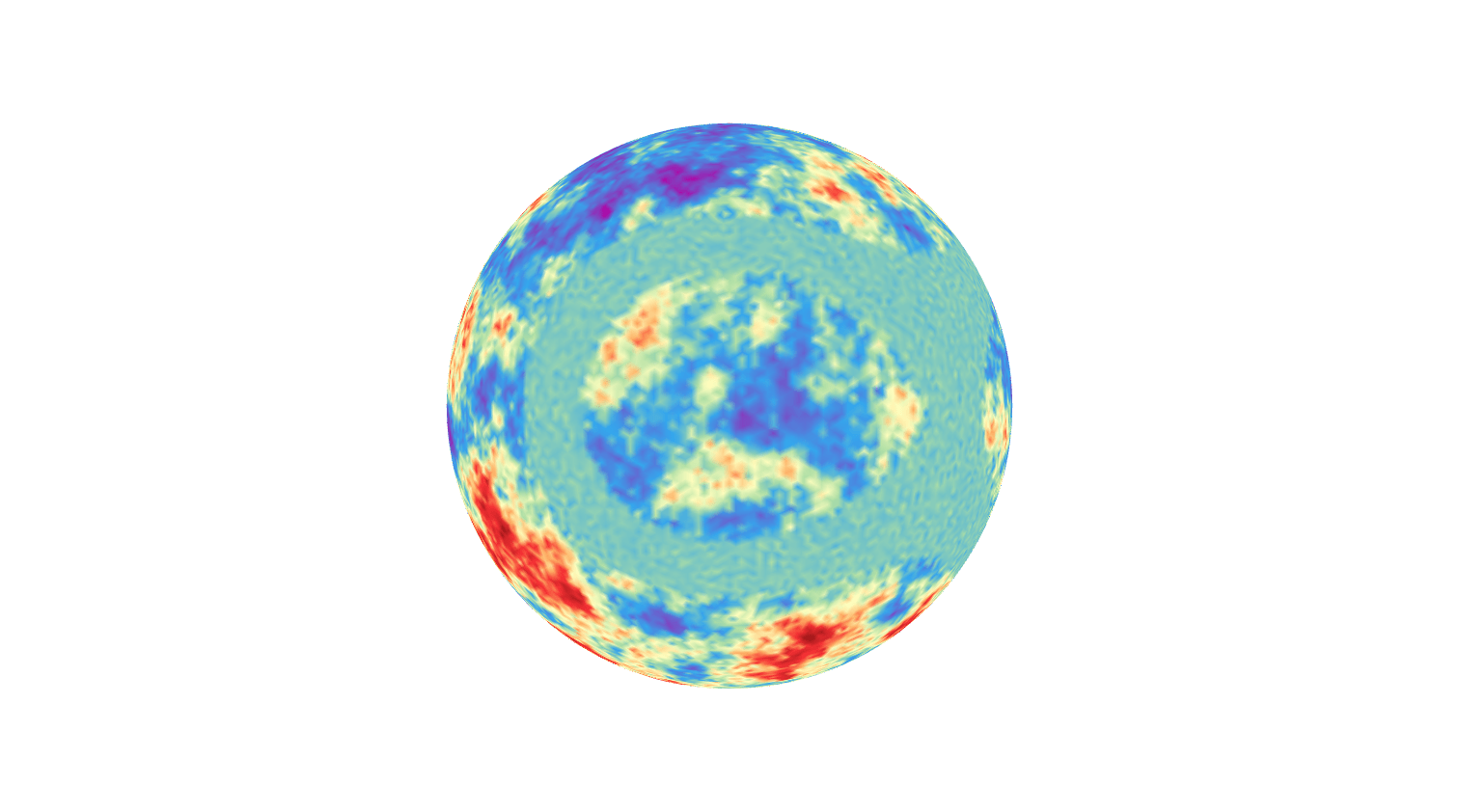
EXTRA: Concrete example III

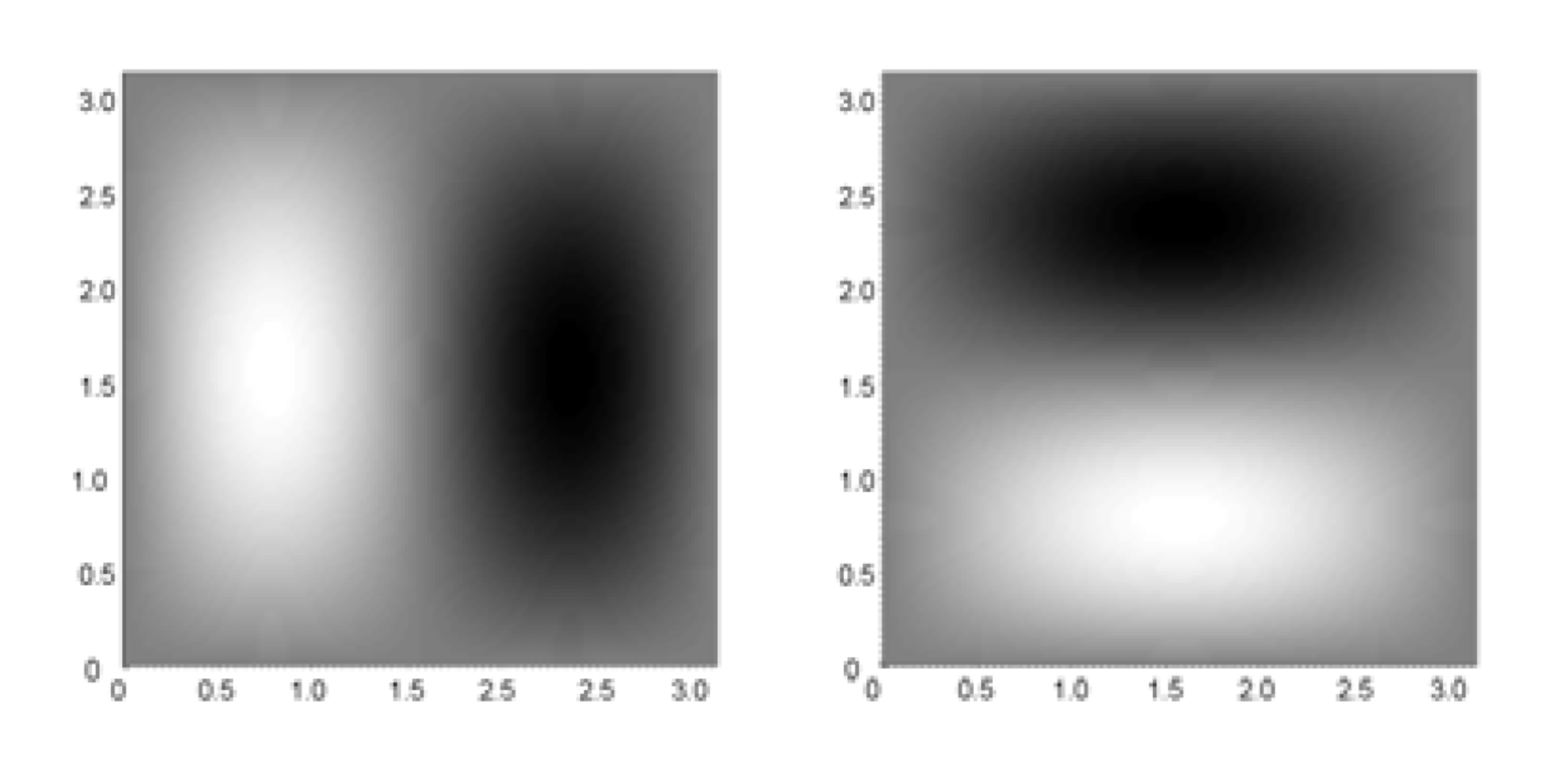
D(x)\nabla_{ \mathbb S^2} u = {\color{red} ρ_1}(\nabla_{ \mathbb S^2} f (x) \cdot \nabla_{ \mathbb S^2} u)\nabla_{ \mathbb S^2} f (x) \\ \qquad+ {\color{blue} \rho_2 }(x \times \nabla_{ \mathbb S^2} f (x) \cdot \nabla_{ \mathbb S^2}u )(x \times \nabla_{ \mathbb S^2} f (x) )

\(\rho_1\) small, \(\rho_2\) large: field is elongated tangentially along level sets of \(f\)

\(\rho_1\) large, \(\rho_2\) small: field is elongated orthogonally along level sets of \(f\)

\mathcal M = \mathbb{S}^2, \gamma(\lambda) = \lambda^{-0.75}

V(x) = 10 \\ f(x) = x_2, \rho_1 = 1, \rho_2 = 25

\mathcal M = \mathbb{S}^2, \gamma(\lambda) = \lambda^{-0.75}

EXTRA: Concrete example III

EXTRA: More details on the model

D \colon T_x \mathcal M \to T_x \mathcal M \\ V \colon \mathcal M \to \mathbb R^+

Eigenpairs of \( \mathcal{L} \): \((\lambda_i,e_i)\)

\mathsf A_{\mathcal M}(u,v) = \int_{\mathcal M} D \nabla_{\mathcal M} u {\cdot} \nabla_{\mathcal M} v \mathrm d x {+} \int_{\mathcal{M}} V uv \mathrm d x

+ Conditions

\(\mathsf A_\mathcal{M}\) defines elliptic operator \(\mathcal L\)

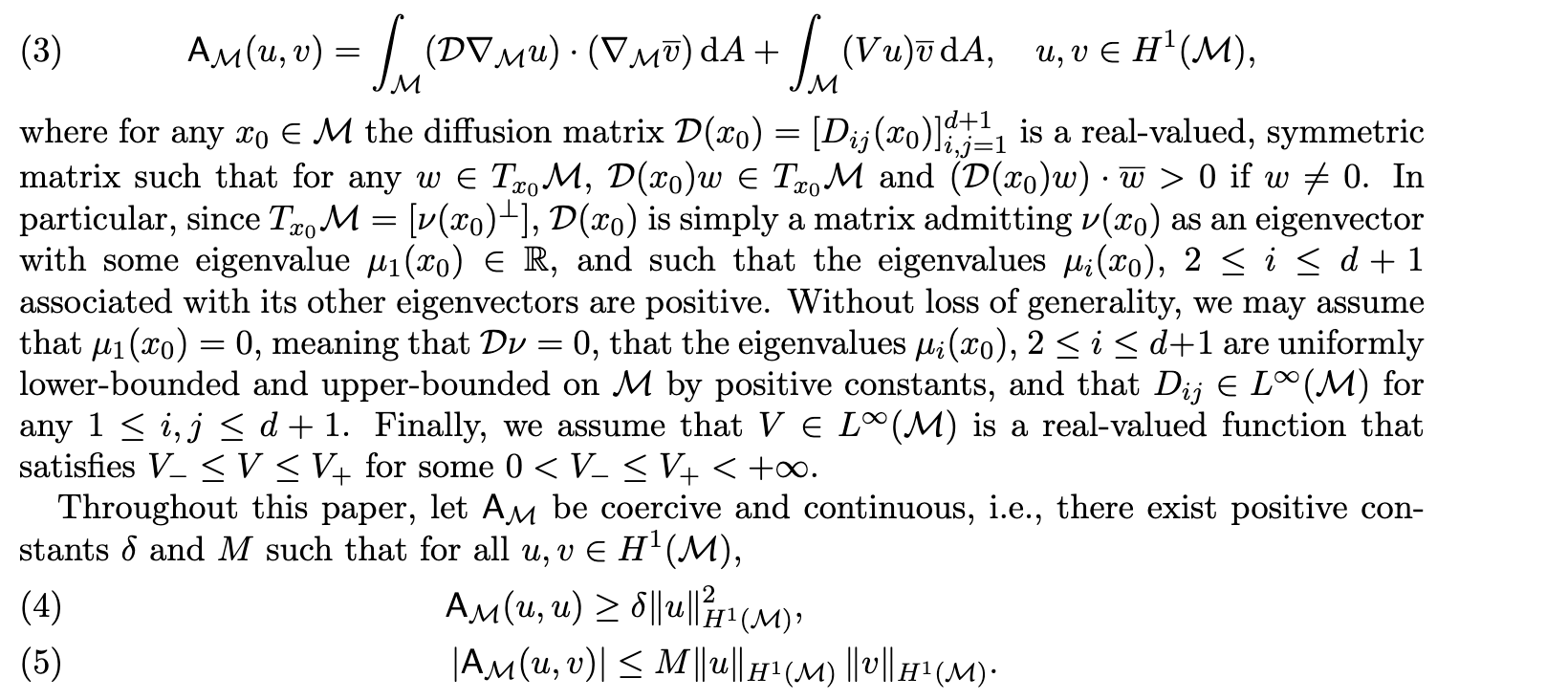
EXTRA: More details on the model

EXTRA: FEM operators

Discretization of operators

\mathcal M, \, H^{1}(\mathcal M)

Original

\mathcal{L}

Eigenpairs

(\lambda_i,e_i)

Discrete 1

\mathcal M, \, S_h^\ell

\mathcal{L}_h

Eigenpairs

(\lambda_{i,h},e_{i,h})

Discrete 2

\mathcal M_h, \, S_h

\mathsf L_h

Eigenpairs

(\Lambda_{i,h},E_{i,h})

EXTRA: Why you shouldn't use the EFs

Error analysis:

Problem:

\sum_{i\in\N}\gamma(\lambda_{i})W_ie_i - \sum_{i=1}^{N_h} \gamma(\Lambda_{i,h})\overline{W}_i E_{i,h}

\|e_i-E_{i,h}\|_{L^2} ??

Generally: Approximating eigenfunctions are hard!

Eigenvalues are fine, however!

EXTRA: Why you shouldn't use the EFs

Generally: Approximating eigenfunctions are hard! Multiplicity!

From D. Boffi, Acta Num. (2010)

EXTRA: The matrices involved

Z \sim N(0,\Sigma_Z)

\Sigma_Z = \sqrt{C}^{-T} \gamma^2(S) \sqrt{C}

C_{kl} = (\psi_k,\psi_l)_{L^2(\mathcal M_h)}

R_{kl} = \mathsf{A}_{\mathcal M_h}(\psi_k,\psi_l)

S = \sqrt{C}^{-1} R \sqrt{C}^{-T}

Chebyshev quadrature approximation of \(\gamma\)

Various white noise approximations, various approximations of \(\mathcal Z\)

\widetilde{\mathcal W} = P_h \mathcal W \, (\in S_h^\ell)

\widetilde{\mathcal Z}_h = \gamma(\mathcal L_h )P_h \mathcal W

\hat{\mathsf{W}} = \mathsf P_h (\sigma \widetilde{\mathcal{W}}^{-\ell})

\mathsf W = \mathsf P_h (\sigma^{1/2} \widetilde{\mathcal{W}}^{-\ell})

\hat{\mathsf{Z}}_h = \gamma(\mathsf L_h )\hat{\mathsf W}

\mathsf{Z}_h = \gamma(\mathsf L_h )\mathsf W

\mathsf{Z}_h = \sum_{i=1}^{N_h} \gamma(\Lambda_{i,h})\overline{W}_i E_{i,h}

EXTRA: A small note on the proof...

\widetilde{\mathcal Z} = \gamma(\mathcal L ) \mathcal W

\hat{\mathsf{Z}}_h = \gamma(\mathsf L_h )\hat{\mathsf W}

\mathsf{Z}_h = \gamma(\mathsf L_h )\mathsf W

\widetilde{\mathcal Z}_h = \gamma(\mathcal L_h )P_h \mathcal W

EXTRA: A small note on the proof...

Important result: errors on the form

\(\|\gamma(\mathcal L)f -\gamma(\mathcal L_h) f\|_{L^2}\)

Brief note on proof:

\gamma(\mathcal L) f = \frac{1}{2\pi i } \int_{\Gamma} \gamma(z)(z-\mathcal{L})^{-1}f \\ \gamma(\mathcal L_h) f = \frac{1}{2\pi i } \int_{\Gamma} \gamma(z)(z-\mathcal{L}_h)^{-1}f

Extra slides: paper III

Geometry of LP systems

Isospectrality

geometric structure of stochastic LP

why not Itô?

proof of convergence, some more details

EXTRA: Geometry of LP systems

Important geometric structure:

LP Systems evolve on coadjoint orbits

(symplectic manifolds that foliate space!)

+ Several preserved quantities, Hamiltonian, Casimirs etc.

\mathcal{O}_{X} = \{g^* X (g^*)^{-1}\colon g \in G\}

Coadjoint orbits

Dynamics on orbit

EXTRA: Geometry of LP systems

\(G \subset \operatorname{GL}(n)\) is compact, simply connected and \(J\)-quadratic, i.e., \(A \in \mathfrak{g} \iff AJ + JA^* = 0 \)

Examples: \(\mathfrak{so}(N), \mathfrak{su}(N), \mathfrak{sp}(N)\).

In this setting, LP flow is isospectral:

\, \dot X_t = [\nabla H(X_t)^*, X_t] \,

EXTRA: Stochastic LP systems

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~

Why Strato?

Why these coefficients?

We need a chain rule

Same bracket-type coefficient: same geometric structure

Stochastic LP Systems evolve on coadjoint orbits and have Casimirs!

EXTRA: Stochastic LP systems

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~

What to assume to prove the existence of solutions?

E.g. Lipschitz is not realistic to assume

But! Some smoothness is sufficient for global existence

System remains on compact level sets of Casimirs
\(\rightarrow\) truncation argument to prove existence

EXTRA: Stochastic LP systems

Stochastic LP Systems evolve on coadjoint orbits and have Casimirs!

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~

Coadjoint orbits

With transport noise

With non-transport noise

EXTRA: Stochastic LP systems

What happens if we apply an off the shelf integrator?

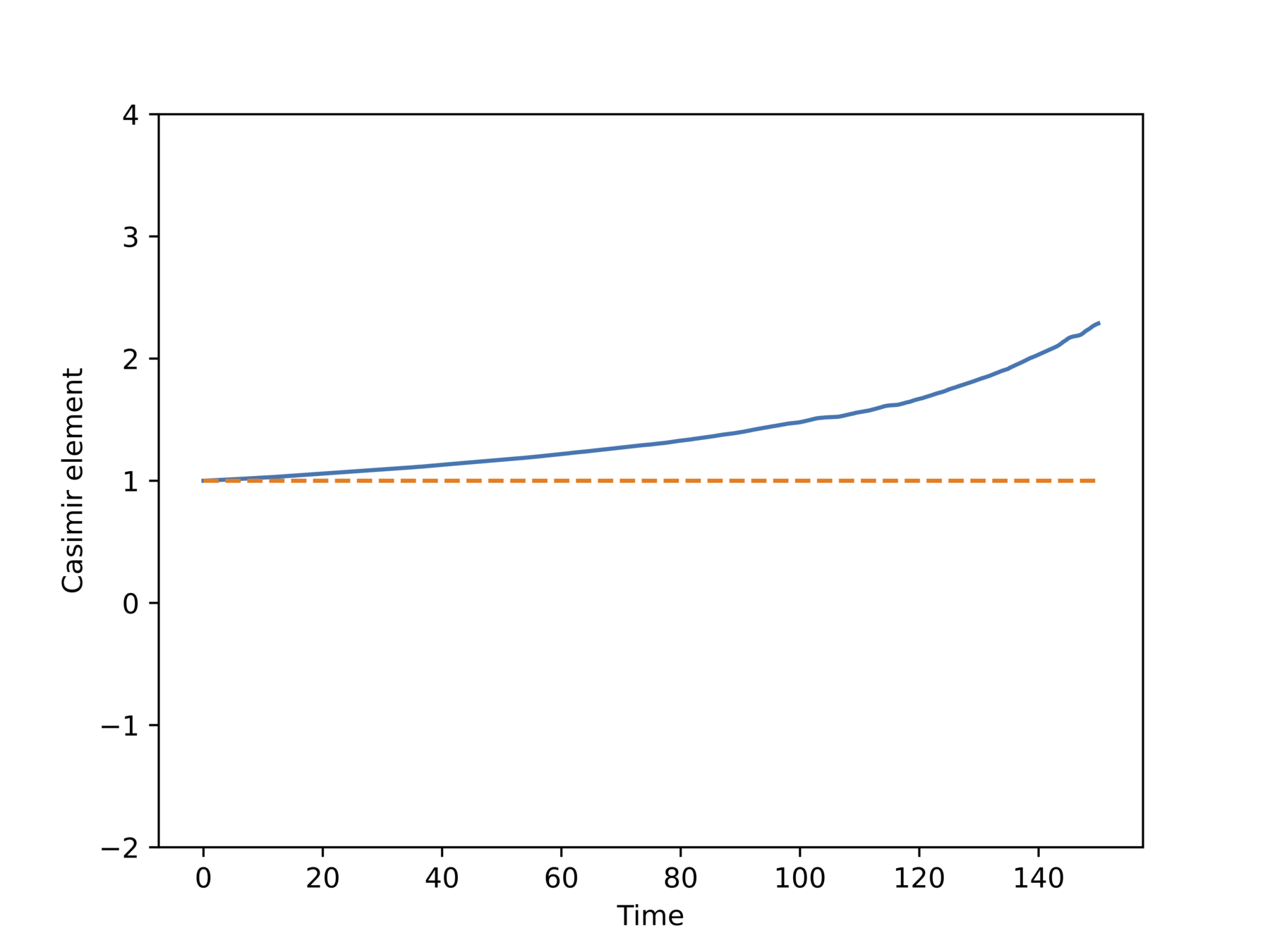
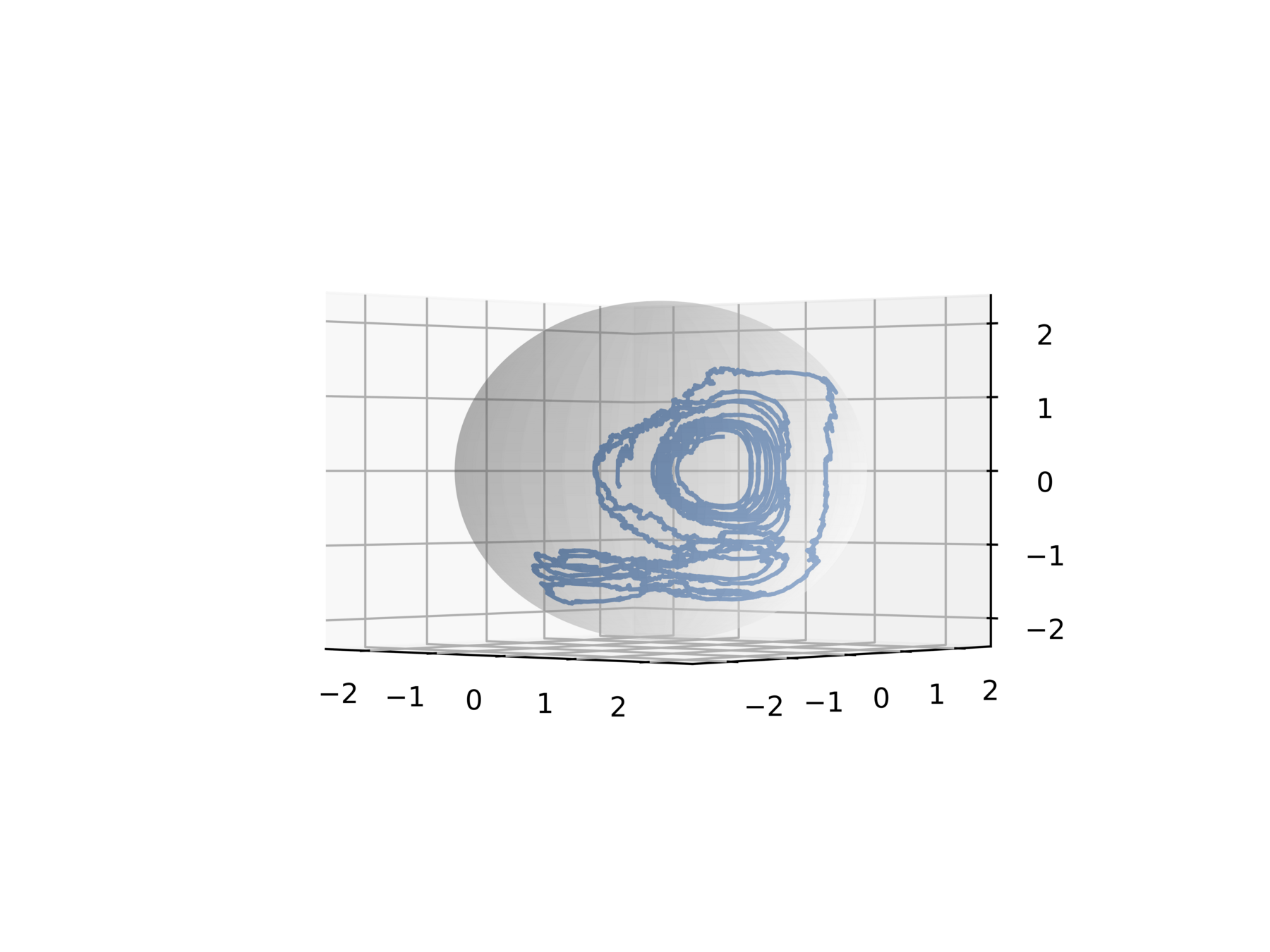
Non-physical behavior!

EXTRA: Stochastic LP systems

What happens with structure-preserving integrators?

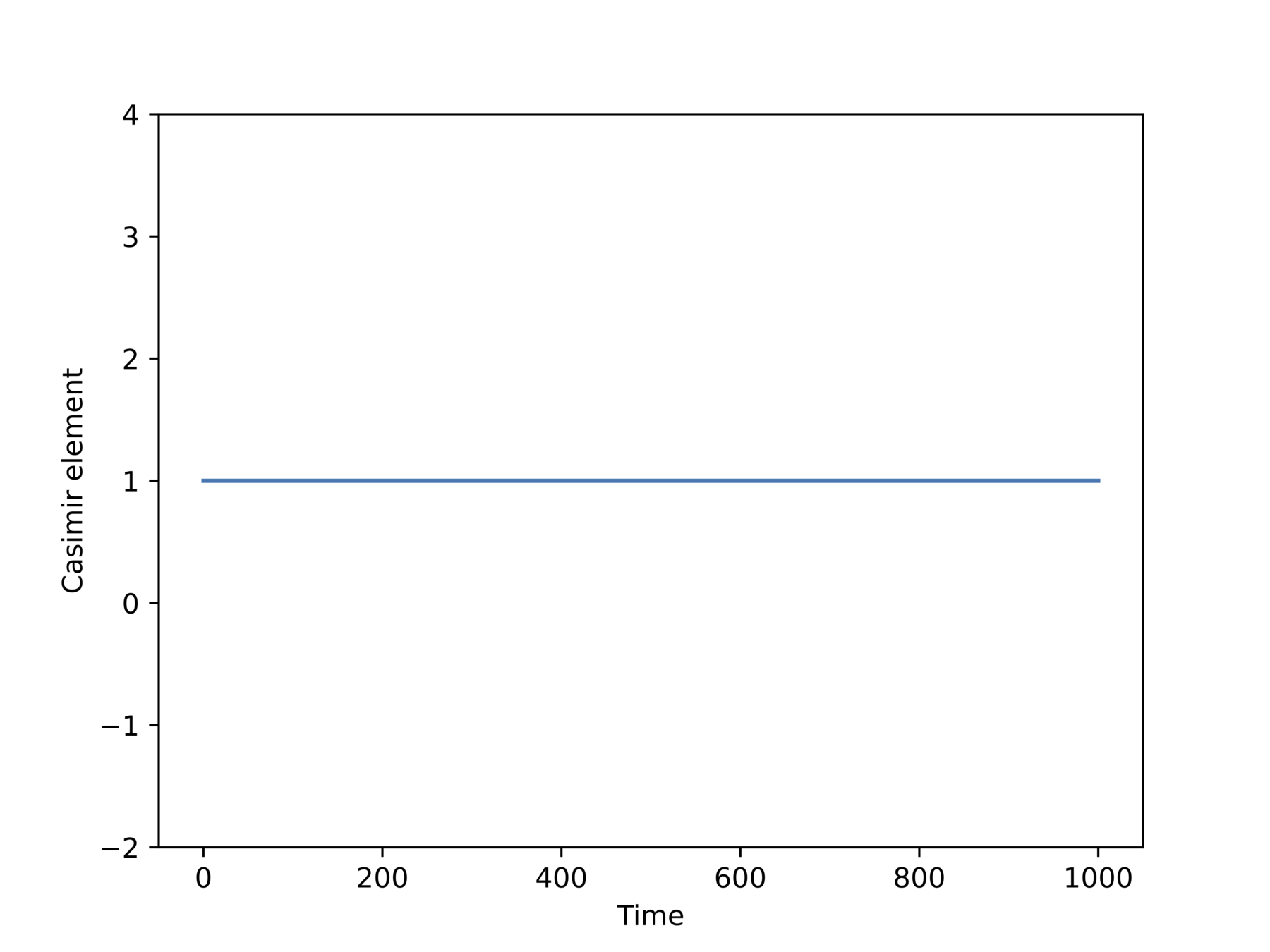
EXTRA: Unreducing LP systems

Intuitive picture: implicit midpoint in disguise

unresolved unscientific question: if implicit midpoint could wear a disguise, how would it wear it?

\begin{split} \Phi_h^{(1)} &\colon \begin{cases} Q_n & = \tilde{Q}- \frac{1}{2}\left( f_0(\tilde{Q}, \tilde{P}) h + \sum_{i=1}^M f_i(\tilde{Q}, \tilde{P})(\zeta_{i})_n \sqrt{h}\right), \\ P_n & = \tilde{P}-\frac{1}{2}\left(k_0(\tilde{Q}, \tilde{P}) h + \sum_{i=1}^M k_i(\tilde{Q}, \tilde{P})(\zeta_{i})_n\sqrt{h} \right), \end{cases} \\ \Phi_h^{(2)} &\colon \begin{cases} Q_{n+1} & = \tilde{Q} + \frac{1}{2}\left( f_0(\tilde{Q}, \tilde{P}) h + \sum_{i=1}^M f_i(\tilde{Q}, \tilde{P})(\zeta_{i})_n \sqrt{h}\right), \\ P_{n+1} & = \tilde{P}+\frac{1}{2}\left(k_0(\tilde{Q}, \tilde{P}) h + \sum_{i=1}^M k_i(\tilde{Q}, \tilde{P})(\zeta_{i})_n\sqrt{h} \right), \end{cases} \end{split}\\ \Phi_h = \Phi_h^{(2)} \circ \Phi_h^{(1)}

Note: No a priori guarantee that this system remains on \(T^*G\)!

Embedded into \((R^{n \times n})^2\) but remains on \(T^*G\)

\(X_t = \mu(Q_t,P_t) \in \mathfrak{g}^*\) satisfies

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~

EXTRA: Integration with tears

\zeta_h = \begin{cases} & A_h \quad \text{if } ~ \xi>A_h, \\ &-A_h \quad \text{if } ~ \xi<-A_h,\\ & \xi \quad \text{if} ~ |\xi| \leq A_h, \end{cases}

Symplectic
Equivariant
Well-studied

EXTRA: Integration with tears

Stochastic isospectral midpoint:

Take \(Q_n,P_n\) such that \(\mu(Q_n,P_n) = X_n\)

Take \(X_{n+1} = \mu(\Phi_h(Q_n,P_n))\)

Extra: Error analysis with tears

1) Show that the implicit midpoint method does not travel too far:

\(\sup_{h \geq 0} \sup_{n \geq 0} \|Q_n,P_n\| \leq R(Q_0,P_0). \)

2) Truncate the CHS system on \(T^*G\)

Upstairs

Downstairs

3) Apply error analysis from literature

Reduction by \(\mu\)

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~

4) Convergence of method for truncated LP system

Strong convergence: \(\mu\) is Lipschitz
Weak convergence: \(\phi \circ \mu\) is valid test func

5) Truncated LP system = LP system

Recipe:

Extra: Error analysis with tears

Assume: \(H_0 \in C^4\) and \(H_1,H_2, \ldots, H_M \in C^5\).
\(T>0\): be a fixed final time,
\(N \in \mathbb{N}\): number of steps
\(X_0 \in \mathfrak{g}^*\): Deterministic initial condition
\(\phi \in C^5\): Test function

~\sup_{0 \leq n \leq N} \mathbb E\left[ \|X(hn)-X_n\|^2\right]^{1/2} \leq \kappa h^{1/2}\\ \sup_{0 \leq n \leq N} \left|\mathbb E[\phi(X(hn))-\phi(X_n)]\right| \leq \kappa h~

Extra: Error analysis with tears

Assume: \(H_0 \in C^4\) and \(H_1,H_2, \ldots, H_M \in C^5\).
\(T>0\): be a fixed final time,
\(N \in \mathbb{N}\): number of steps
\(X_0 \in \mathfrak{g}^*\): Deterministic initial condition
\(\phi \in C^5\): Test function

~\sup_{0 \leq n \leq N} \mathbb E\left[ \|X(hn)-X_n\|^2\right]^{1/2} \leq \kappa h^{1/2}\\ \sup_{0 \leq n \leq N} \left|\mathbb E[\phi(X(hn))-\phi(X_n)]\right| \leq \kappa h~

Extra: Error analysis with tears

~\sup_{0 \leq n \leq N} \mathbb E\left[ \|X(hn)-X_n\|^2\right]^{1/2} \leq \kappa h^{1/2}\\ \sup_{0 \leq n \leq N} \left|\mathbb E[\phi(X(hn))-\phi(X_n)]\right| \leq \kappa h~

Geometric structure of equations and its preservation is central. Used to prove

Existence and uniquness
Convergence

Without structure preservation, no convergence guarantees

Extra slides: IsoMP vs other methods

Explicit methods based on splitting for separable Hamiltonians
Extend to \(T\operatorname{GL}(n)\), use symplectic RATTLE
Symplectic Lie group methods on \(T^* G\), map back and forth with exponential map
Collective symplectic integrators

IsoMP works directly on algebra
no constraints
no algebra-to-group mappings
works for large class of Hamiltonians

Extra slides: generalities on shape matching

How to match?

Idea: Use a distance \(d_V\colon V \times V \to \mathbb R\) on \(V\), look for \(g \in G\) that solves

\min_{g \in G} d_V(g\cdot A, B)

How to match \(A \in V \) with \(B \in V\)?

Problem: In general, no \(g\) takes \(A\) to \(B\) \(\implies\)

more and more complex warps of \(A\)

(the action is non-transitive).

Regularize!

\min_{g \in G} d_V(g\cdot A, B)

Regularize!

\min_{g \in G} d_V(g\cdot A, B)+\lambda d_G(e,g)

Add a regularization term!

Penalize strange deformations

How to compute \(d_G(e,g)\)?

Pricey! An optimization problem in itself!

The simpler way: Let \(d_G\) be the distance function of a right-invariant Riemannian metric and generate \(g\) as a curve! (Geometry!)

Let it flow

\min_{\gamma(t)} d_V(\gamma(1) \cdot A, B)+\lambda \int_0^1 \langle \dot \gamma(t) ,\dot \gamma(t)\rangle_{\gamma(t)}

\dot \gamma(t) = \mathrm d R_{\gamma(t)} {\color{black}\nu(t)}, \gamma(0) = e

Let it flow

\min_{\gamma(t)} d_V(\gamma(1) \cdot A, B)+\lambda \int_0^1 \langle \dot \gamma(t) ,\dot \gamma(t)\rangle_{\gamma(t)}

\dot \gamma(t) = \mathrm d R_{\gamma(t)} {\color{#a64d79}\nu(t)}, \gamma(0) = e

\({\color{#a64d79}{\nu}}\colon [0,1] \to \mathfrak{g}\) is a curve in the vector space \(\mathfrak{g}\)!

Let right-invariance strike!

Let it flow

\min_{\nu(t)} d_V(\gamma(1) \cdot A, B)+\lambda \int_0^1 L \langle \nu ,\nu \rangle_e\mathrm{d}t

\dot \gamma(t) = \mathrm d R_{\gamma(t)} {\color{#a64d79}\nu(t)}, \gamma(0) = e

An optimization problem over curves in a vector space!

\({\color{#a64d79}{\nu}}\colon [0,1] \to \mathfrak{g}\) is a curve in the vector space \(\mathfrak{g}\)!

Let right-invariance strike!

Extra: Ingredients for shape analysis

A Lie group of deformations \(G\) acting on a set of shapes \(V\) (metric space)
A fidelity energy that evaluates the closeness of two shapes
A regularization energy that penalizes aggresive deformations

d_V(\gamma(1).A,B)

Flexible choice

\langle \dot \gamma, \dot \gamma\rangle_\gamma = (\dot \gamma \circ \gamma^{-1}, \dot \gamma \circ \gamma^{-1})_{\mathfrak{g}}

Right-invariant metric (not so flexible)

Extra slides: paper IV

Extra: Paper IV

In usual LM, all vector fields are available

Idea: Constrain set of vector fields

Sub-Riemannian landmark matching!

Landmark matching:

\(V = (\mathbb{T}^2)^N\),

\(G = \operatorname{Diff}(\mathbb{T}^2)\)

Extra: Paper IV

v \in \mathcal{S} \iff \exists u \in \mathcal{U} \text{ s.t. } v(x) = F(u)(x)

\(\mathcal{S}\)

\(v = F(u)(x)\)

\(\mathfrak{X}(M)\)

\(F(u)\)

\(\mathcal{U}\)

\(u\)

Extra: Paper IV

v \in \mathcal{S} \iff \exists u \in \mathcal{U} \text{ s.t. } v(x) = F(u)(x)

\(\mathcal{S}\)

\(v = F(u)(x)\)

\(\mathfrak{X}(M)\)

\(F(u)\)

\(\mathcal{U}\)

\(u\)

Extra: Paper IV

Dynamics of \(u\) are determined from the dynamics of \(v\)

Instead of optimizing over vector fields, optimize over \(\mathcal{U}\)

\(\mathcal{U}\) is finite dimensional \(\implies\) discretization

How to find dynamics of \(u\)?

Idea: Apply chain rule to \(\dot m = \operatorname{ad}_v^T m\)

Extra: Paper IV

A(u)\dot u = (D_u^T m \circ L^{-1}) \cdot \operatorname{ad}^T_v m

\dot m = \operatorname{ad}^T_v m +L\mathcal{M}(u)

\(\mathcal{S}\)

\(v = F(u)(x)\)

\(\mathfrak{X}(M)\)

\(F(u)\)

\(\mathcal{U}\)

\(u\)

Extra: Paper IV

Connected to neural networks!

Infinite number of layers \(\implies\)

Time-continuous optimal control problem

\ldots

Skip connection \(\implies \) Explicit Euler

Extra: Paper IV

When matching landmarks, points are moved by a vector field parametrized by some control variable.

A neural networks moves points along a vector field determined by weights and biases.

Extra: Paper IV

Landmarks
Image
Warping new landmarks
Control parameters

Input data, e.g. images
"Meta-image"
Testing
Weights and biases

View networks with shape analysis glasses!

Extra slides: paper V

Extra: Paper V

\mathbb{R}^n

\mu_0

\mu_1

\varphi_* \mu_0

\min_{\varphi \in \operatorname{Diff}(\mathbb{R}^n)} J(\varphi) = \int_{\mathbb{R}^n} |\varphi(x)-x|^2 \mathrm{d}\mu_0(x) \\ \text{s.t. } \varphi \in C(\mu_0,\mu_1) = \{\varphi \in \operatorname{Diff}(\mathbb R^n)| \varphi_* \mu_0 = \mu_1\}

Extra: Paper V

Geometric structure

\operatorname{Diff}(\mathbb R^n)/\operatorname{Diff}_{\mu_0}(\mathbb R^n)\\ \cong \operatorname{Dens}(\mathbb R^n)

In brief: Gradient flow horizontally or vertically

\mu_0

\mu_1

\text{Id}

\operatorname{Dens}(\mathbb{R}^n)

\operatorname{Diff}(\mathbb{R}^n)

(More info: Modin, 2017 and references therein)

Gaussian Monge Problem:

\(\mu_0\) and \(\mu_1\) are both (zero-mean) normal distributions on \(\mathbb{R}^n\).

Normal distributions \(\cong\) \(P(n)\), positive-definite symmetric matrices

\mu_0

\mu_1

\mathcal{N}(0,\Sigma_0)

\mathcal{N}(0,\Sigma_1)

\min J (A ) = \operatorname{Tr}((I - A )\Sigma_0 (I - A )^T ) \\ \text{s.t. } A\Sigma_0 A^T = \Sigma_1

Extra: Paper V

\mu_1

Extra: Paper V

\operatorname{GL}(n)/\operatorname{O}(\Sigma_0,n)\\ \cong \operatorname{P}(n)

\Sigma_0

\Sigma_1

\text{Id}

\operatorname{P}(n)

\operatorname{GL}(n)

In brief: Gradient flow horizontally or vertically

Extra: Paper V

\Sigma_1

How to prove convergence?

Idea: Show \(\frac{\mathrm d} {\mathrm d t} J \to 0\), and that this means we hit polar cone

\dot B = \Omega B, B(0) =A \\ \Sigma_1 \Omega + \Omega_1 \Sigma = 2\Sigma_1 (B^{-1}-B^{-T}) \,

Extra slides: paper VI

Shooting,

Gradient

Quantitative results

The dynamic formulation

~\dot m = \operatorname{ad}_v^* m~ \\ m = L\nu

Matching by shooting

Recall example II from intro: reduction to dynamic formulation is made easy by right-invariance

Shape for Cryo-EM

Gradient is available

Extra: three deformations

Deformed

Target

Template

Extra: quantitative

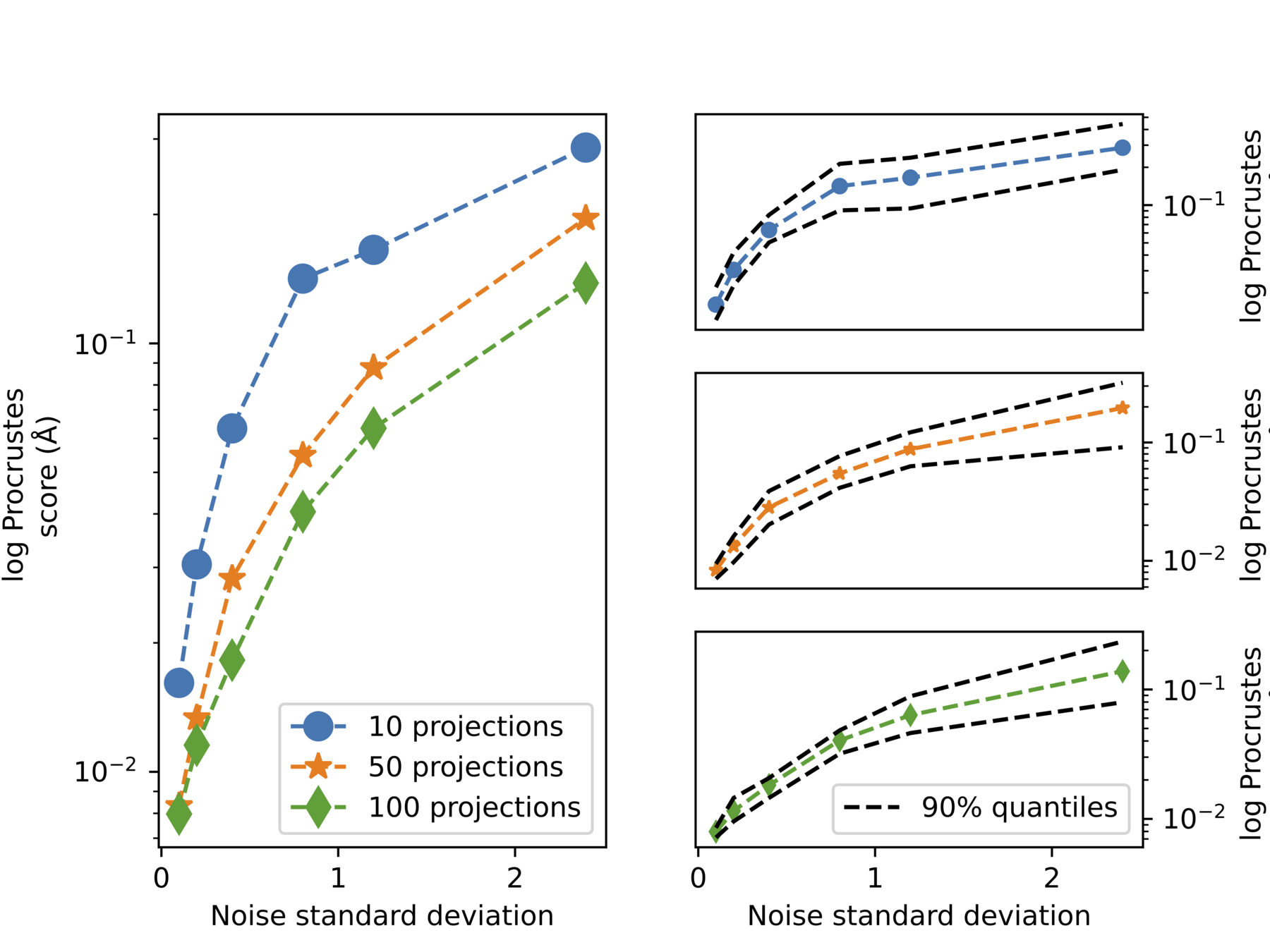
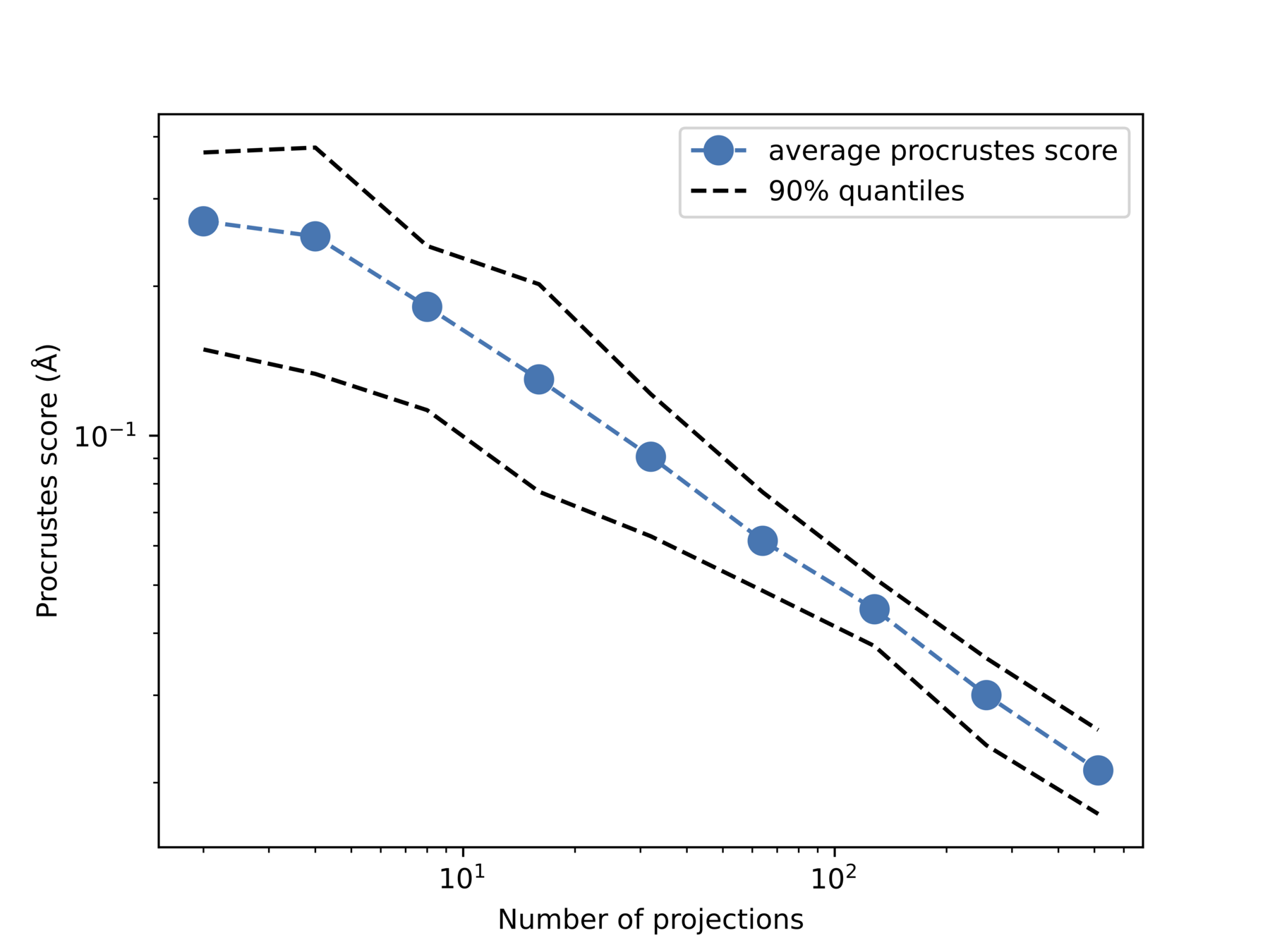
Increase noise

Increase #projections

Quantative measure: Procrustes score

Extra slides: paper VII

Euler equations

Zeitlin

Complexified Euler equations

Simulations for Blow-up

Extra: Paper VII

~\dot v + \nabla_v v = -\nabla p ~\\ ~\operatorname{div} v = 0

\omega = \operatorname{curl} v

The \(L^2\)-geodesic equation on \(\operatorname{Diff}_{\mu}(\mathbb{S}^2)\):

~\dot \omega = \{\Delta^{-1} \omega,\omega\}~

Extra: Paper VII

(\mathbb{S}^2,g,\Omega)

\{f,g\} = \Omega(\nabla^\perp f,\nabla^\perp g) = \Omega(X_f,X_g)

Euler eqs: Lie-Poisson system on \(C^\infty_0(\mathbb{S}^2) \cong (\mathfrak{X}_\mu(\mathbb{S}^2))^*\)

G = \operatorname{Diff}_\mu(\mathbb{S}^2)

\mathfrak{g} = X_\mu(\mathbb{S}^2)

=> Sphere is Kähler

~\dot \omega = \{\Delta^{-1} \omega,\omega\}~

Initially for the torus, but we work on the sphere!

Extra: Paper VII

Goal: Find a mapping \(T_N:C_0^\infty(\mathbb{S^2}) \to \mathfrak{su}(N)\) such that:

T_N(\{\cdot,\cdot\}) \approx [T_N(\cdot),T_N(\cdot)]

Hoppe, 1989:

\omega = \sum_{l=0}^\infty \sum_{m=-l}^l a_{l,m} Y_{l,m} \mapsto \sum_{l=0}^N \sum_{m=-l}^l a_{l,m} T^N_{l,m} = W

How to find \(T_{l,m}^N\)?

Extra: Paper VII

Coordinate function representation of \(\mathfrak{so}(3)\) in \((C^\infty_0(\mathbb{S}^2),\{\cdot,\cdot\})\).

e_1,e_2,e_3 \in C^\infty(\mathbb{S}^2)

\Delta = \sum_{i=1}^3 \{e_k,\{e_k,\cdot \}\}

Spin \(s = (N-1)/2\)-representation of \(\mathfrak{so}(3)\) in \(\mathfrak{u}(N)\)

X_1,X_2,X_3 \in \mathfrak{u}(N)

Extra: Paper VII

Hoppe–Yau Laplacian:

\Delta_N = \sum_{i=1}^3 [X_k,[X_k,\cdot ]]

Hoppe–Yau (1998):

The first \(N^2\) eigenvalues of \(\Delta\) coincides with those of \(\Delta_N\)

\(T_{l,m}^N\) are eigenfunctions to \(\Delta_N\)

\omega \mapsto \sum_{l=0}^N \sum_{m=-l}^l a_{l,m} T^N_{l,m} = W

Extra: Paper VII

\omega_{ij}

\omega_{ij}^T

Extra: Paper VII

Quantized system on \(\mathfrak{su}(N)\):

~\dot W= [P,W]~\\ P = \Delta_N^{-1} W

Continuous system on \(C^\infty_0(\mathbb{S}^2)\):

\dot \omega = \{{\psi},\omega\}\\ \psi = \Delta^{-1} \omega \\

T_N(\omega) = \sum_{l=0}^N \sum_{m=-l}^l a_{l,m} T^N_{l,m} = W \\ T_N(\{\cdot,\cdot\}) \approx [T_N(\cdot),T_N(\cdot)]

Extra: Paper VII

Canonical expression (EP-equations):

\dot \omega = \operatorname{ad}_\psi^* \omega = \{\bar{\psi},\omega\}_{\mathbb{C}}

Relationship between \(\omega\) and \(\psi \)?

(C^\infty(\mathbb{S}^2;\mathbb{C})/\mathbb{C})^* = C_0^\infty(\mathbb{S}^2;\mathbb{C})

Consider complexified Euler equations as LP system on complexified functions:

Extra: Paper VII

Relationship between \(\omega\) and \(\psi \)?

H(\omega) = \int_{\mathbb{S}^2} v \cdot v \Omega

Determined by Hamiltonian!

Math

\omega = -\Delta \psi

\dot \omega = \{\bar{\psi},\omega\}_{\mathbb{C}} \\ \,\omega = -\Delta \psi \,

Proven to blow up in finite time for toroidal case. Conjecture same is true for numerics

Extra: Paper VII

How to detect in numerics?

Grows very rapidly

How to be sure that the observed behavior is not a numerical artifact?

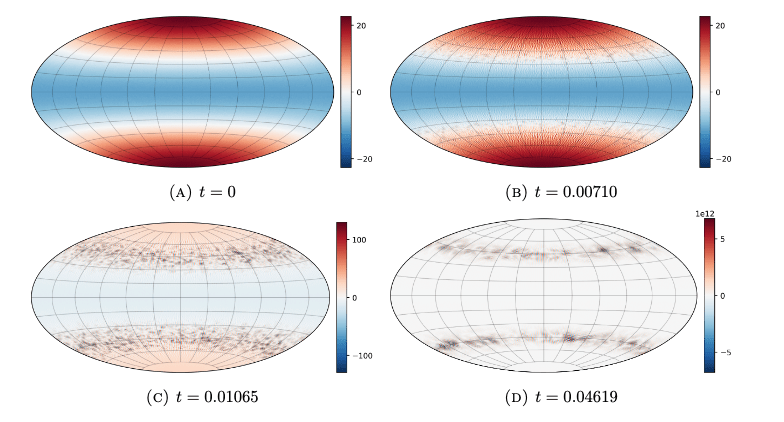
Extra: Paper VII

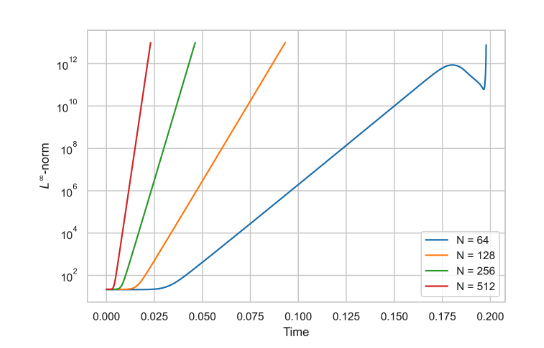
Growth of norm!

Extra: Paper VII

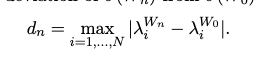
Check spectral deviation

Extra: Paper VII

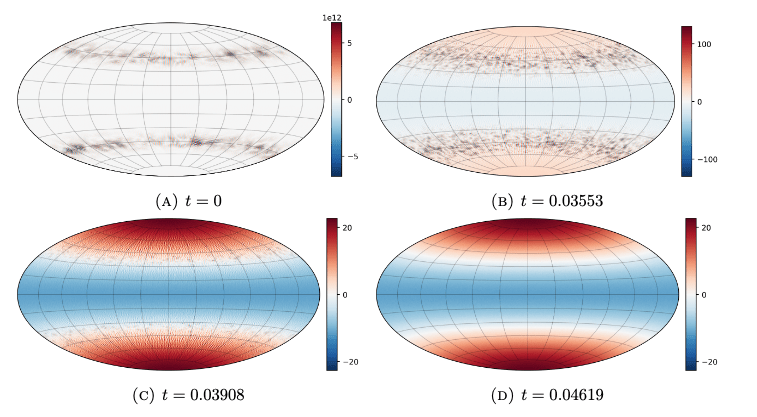
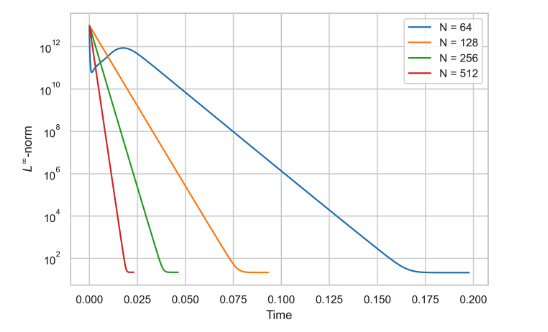
Check reversibility

Extra: Paper VII

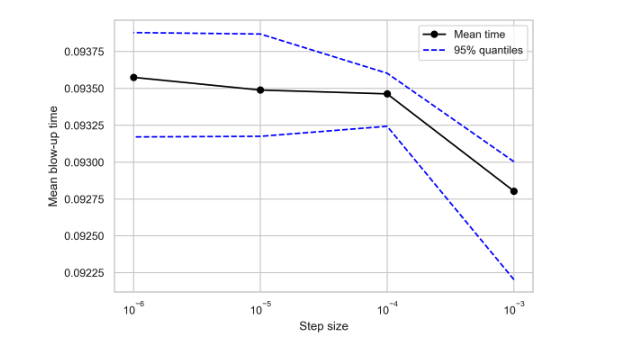
Check mean time to blow up wrt step size -stabilizes

Extra: Paper VII

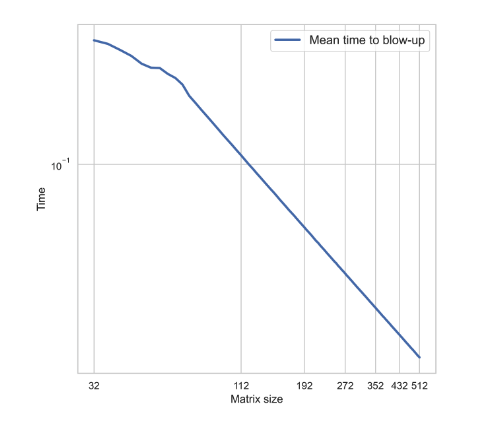
Check mean time to blow up wrt matrix size

Extra: Paper VII: signature

Linear growth after transient phase?

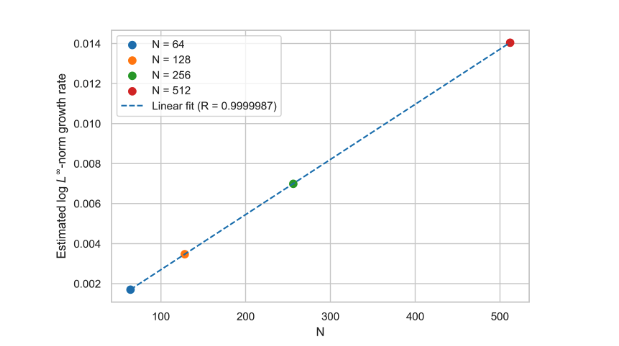
Linear rate vs matrix size - linear relationship

Extra: Paper VII: signature

Extra slides: notes on Zeitlin

Why not the torus?

\,\,e_1(x,y) = x\\ e_2(x,y) = y

e_1(x,y,z) \simeq Y_{1,1}\\ ~~e_2(x,y,z) \simeq Y_{1,-1} \\ e_3(x,y,z) \simeq Y_{1,0}

Generator of isometries: