Generating non-stationary Gaussian random fields on hypersurfaces using surface finite element methods

Erik Jansson

Slides available at slides.com/erikjansson

Stochastic partial differential equations: Statistics meets numerics

IML 2025

Hi!

What stochastics + numerics do I work with?

~\mathcal{Z} = \gamma(\mathcal L) \mathcal{W}~

Random fields via SPDEs/PDE-based colorings

Stochastic LP systems

~ \mathrm d X_t =[\nabla H_0(X_t)^*,X_t] \, \mathrm d t + \sum_{k=1}^M [\nabla H_k(X_t)^*,X_t] \circ \mathrm d W_t^k ~ 

Time but no space

Space but no time

Joint work with:

 

  • Annika Lang (Chalmers/University of Gothenburg)
  • Mike Pereira (Mines Paris - PSL University)

Made possible by:

 

  1. A. Bonito, D. Guignard, and W. Lei, Numerical approximation of Gaussian random fields on
    closed surfaces, Computational and Applied Mathematics. In press (2024)

  2. Dziuk, G., and Elliott, C. M., Finite element methods for surface PDEs. Acta Num., 22:289–396, 2013.

  3. H. Fujita and T. Suzuki, Evolution problems, Handbook of Numerical Analysis, pp. 789–928,

  4. Whittle, P., Stochastic processes in several dimensions. Bull. Inst. Int. Stat., 40:974–994, 1963.

Talk based on:

asdasdasd

 

 

https://arxiv.org//2406.08185

See Audience for Annika

Mike

 

  1. D. Boffi, Finite element approximation of eigenvalue problems, Acta Numerica, pp. 1-120 (2010).

  2. A. Yagi, Abstract Parabolic Evolution Equations and Their Applications, Springer Monographs in Mathematics, Springer, Berlin, 2010.

  3. Bolin, D., Kirchner, K., Kovács, M., Numerical solution of fractional elliptic stochastic PDEs with spatial white noise, IMA J. Numer. Anal., 40(2):1051–1073, 2020 

Bonus references

GRFs on Manifolds

In this talk: Manifolds = compact, boundary–less oriented embedded surfaces or curves in \(\mathbb{R}^3\) or \(\mathbb{R}^2\)

Two questions:

Sampling

Statistics

Elliptic differential operator

White noise

SPDE view:  Consider GRFs that are colorings of white noise by functions of elliptic partial differential operators:

\mathcal Z =\gamma(\mathcal{L}) \mathcal{W}

Elliptic differential operator

White noise

Two questions:

Sampling

Statistics

GRFs on Manifolds

In this talk: Manifolds = compact, boundary–less oriented embedded surfaces or curves in \(\mathbb{R}^3\) or \(\mathbb{R}^2\)

SPDE view:  Consider GRFs that are colorings of white noise by functions of elliptic partial differential operators:

\mathcal Z =\gamma(\mathcal{L}) \mathcal{W}

Two questions:

Computation

Statistics

GRFs on Manifolds

In this talk: Manifolds = compact, boundary–less oriented embedded surfaces or curves in \(\mathbb{R}^3\) or \(\mathbb{R}^2\)

But please reach out re "stats"

Elliptic differential operator

White noise

SPDE view:  Consider GRFs that are colorings of white noise by functions of elliptic partial differential operators:

\mathcal Z =\gamma(\mathcal{L}) \mathcal{W}

The differential operator

D \colon T_x \mathcal M \to T_x \mathcal M \\ V \colon \mathcal M \to \mathbb R^+

Eigenpairs of \( \mathcal{L} \): \((\lambda_i,e_i)\)

\mathsf A_{\mathcal M}(u,v) = \int_{\mathcal M} D \nabla_{\mathcal M} u {\cdot} \nabla_{\mathcal M} v \mathrm d x {+} \int_{\mathcal{M}} V uv \mathrm d x

+ Conditions

\(\mathsf A_\mathcal{M}\) defines elliptic operator \(\mathcal L\)

The Model

~\mathcal{Z} = \gamma(\mathcal L) \mathcal{W}~

\(\gamma\colon\mathbb{R}_+ \to \mathbb{R}\) is a function satisfying sufficient decay properties (plus more)

~\mathcal{Z} = \sum_{i=1}^\infty \gamma(\lambda_i) W_i e_i~
\mathcal{W} = \sum_{i=1}^\infty W_i e_i, W_i \sim \mathsf N(0,1)

The Model

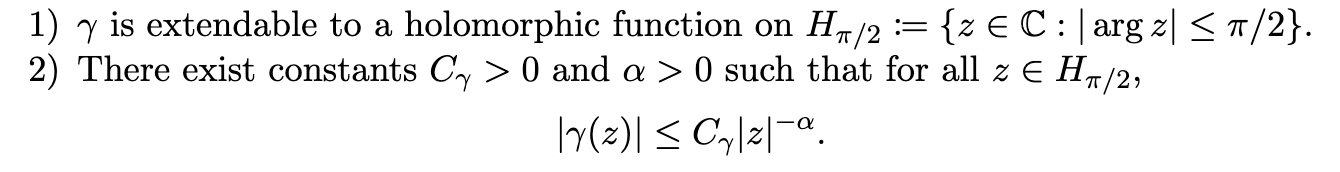
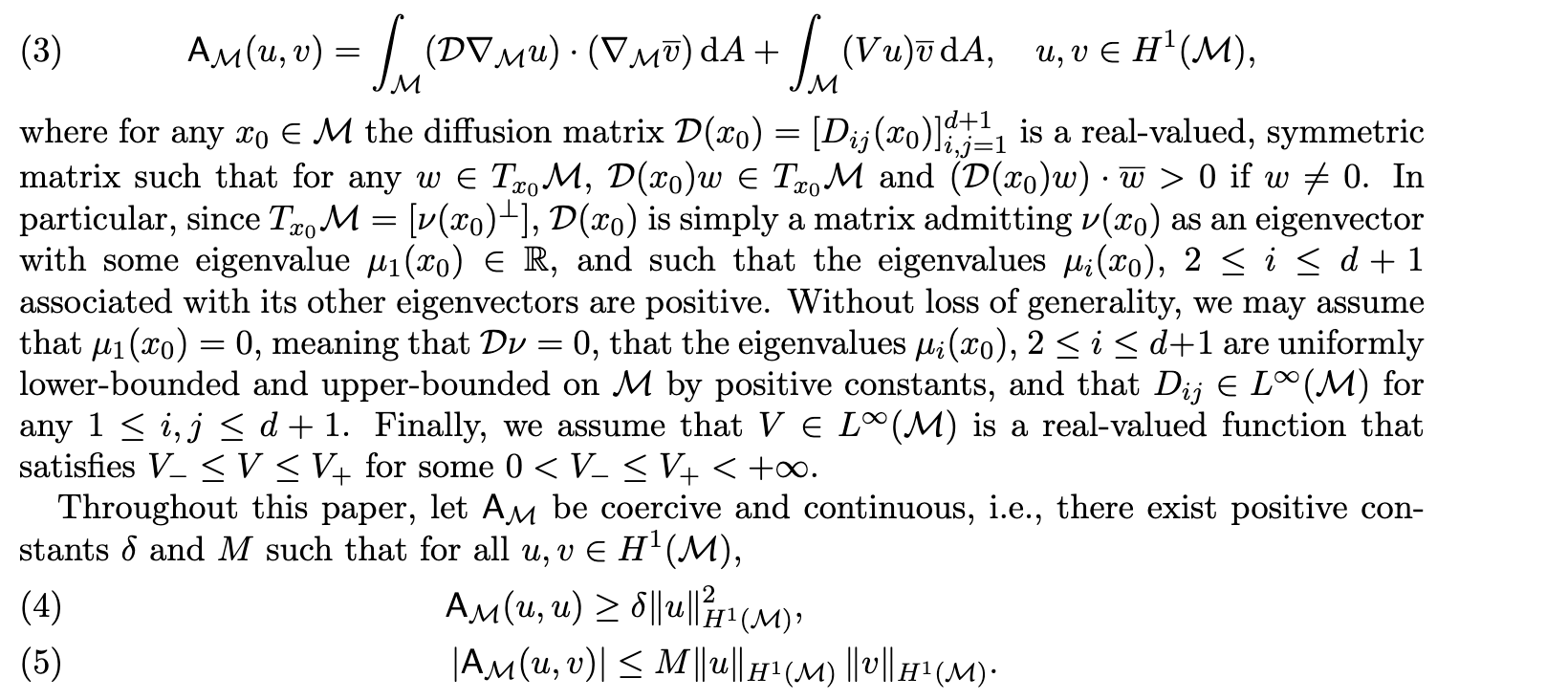
The Model: Example 1

\mathcal M = \mathbb{S}^2, \gamma(\lambda) = \lambda^{-\alpha}, \alpha > 1/2
D_{ij} = \delta_{ij}
V(x) = 10
\alpha = 1.5
\alpha = 0.55

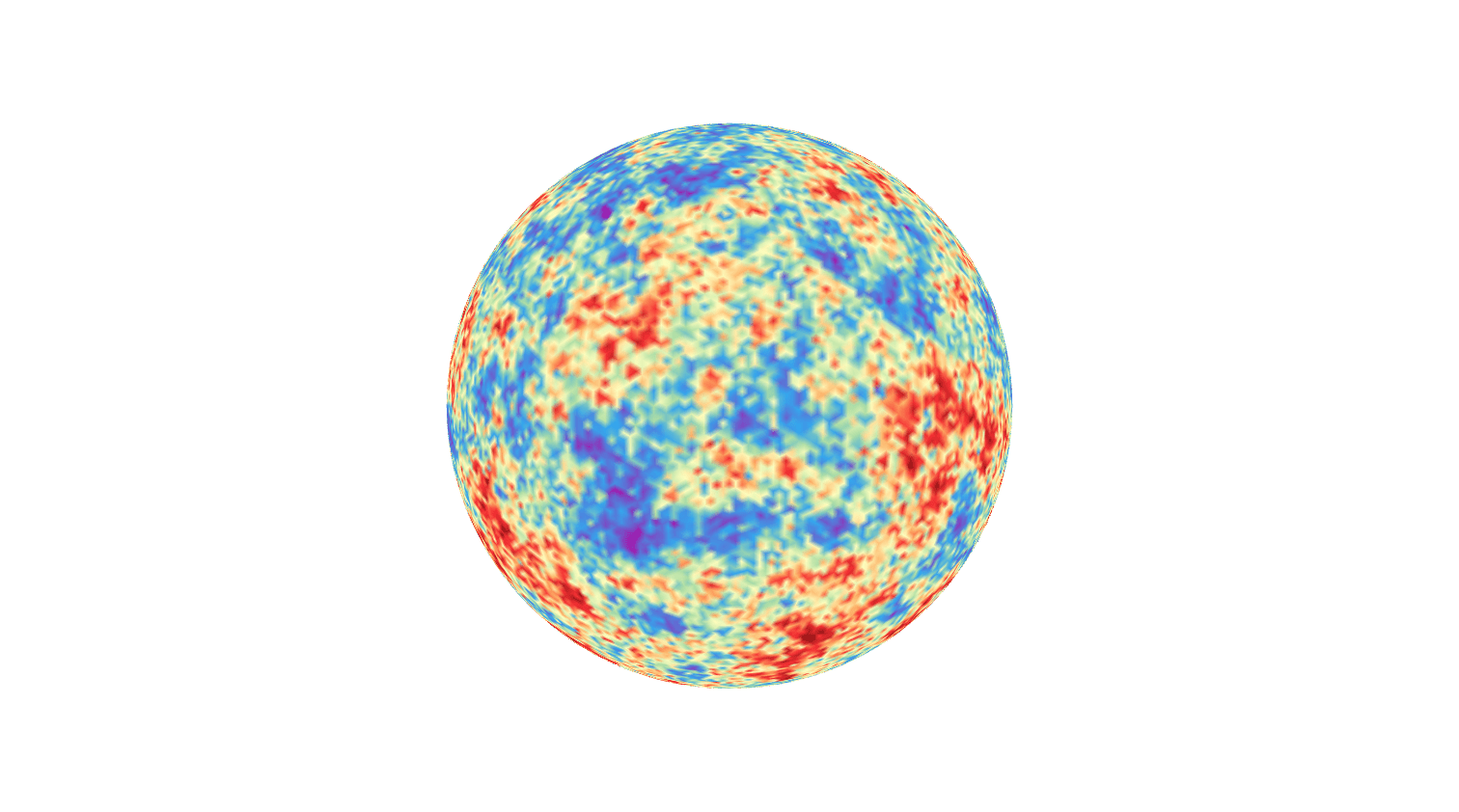
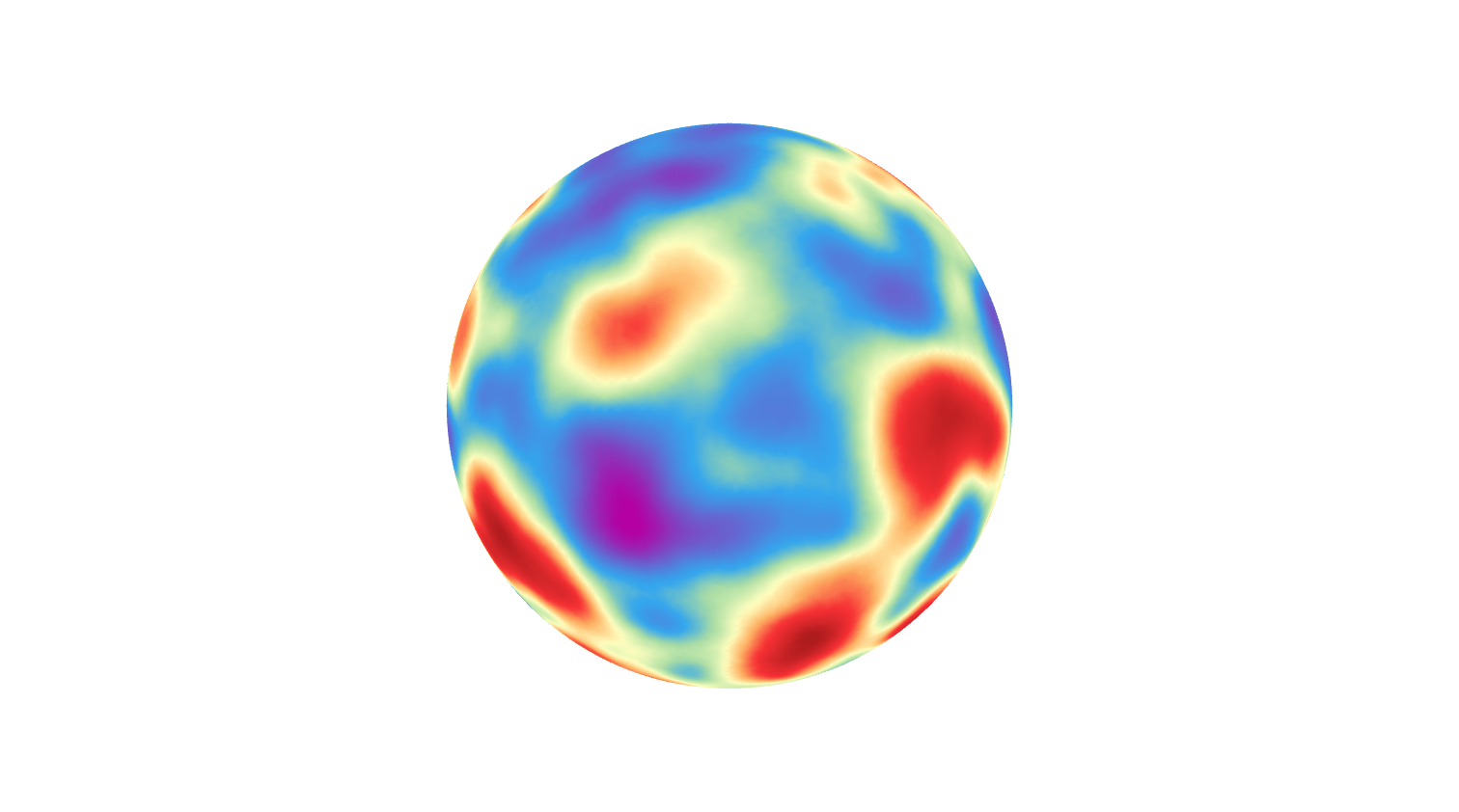
Whittle–Matérn random fields given by SPDE \((\kappa^2-\Delta_{\mathbb{S}^2})^\beta \mathcal Z = \mathcal{W}\)!

\mathcal M = \mathbb{S}^2, \gamma(\lambda) = \lambda^{-0.75}
D_{ij} = \delta_{ij}
V(x) = \begin{cases} 10^5 \quad \text{if } x_2^6+x_1^3-x_3^2 \in (0.1,0.5)\\ 10 \quad \text{else} \end{cases}

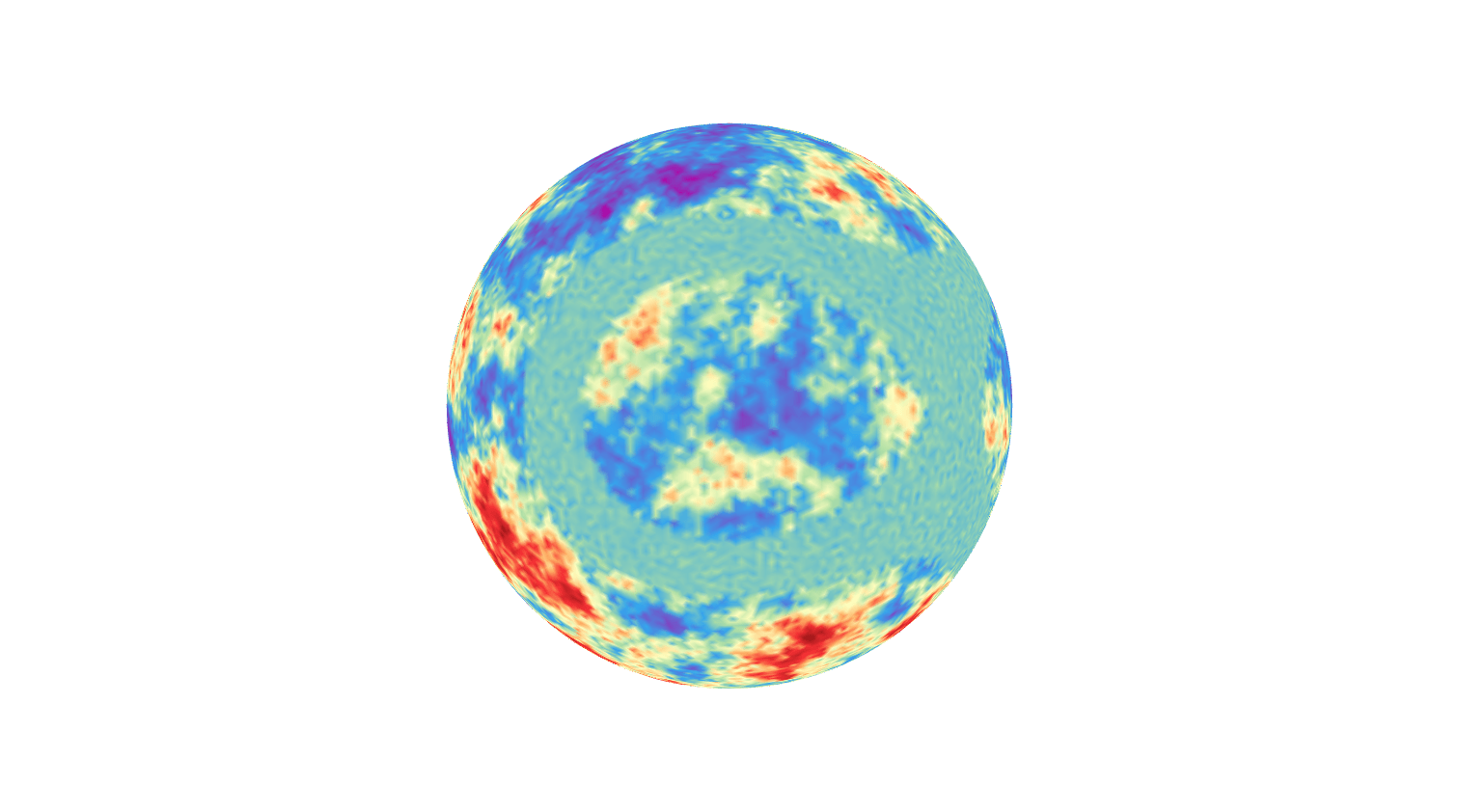
The Model: Example 2

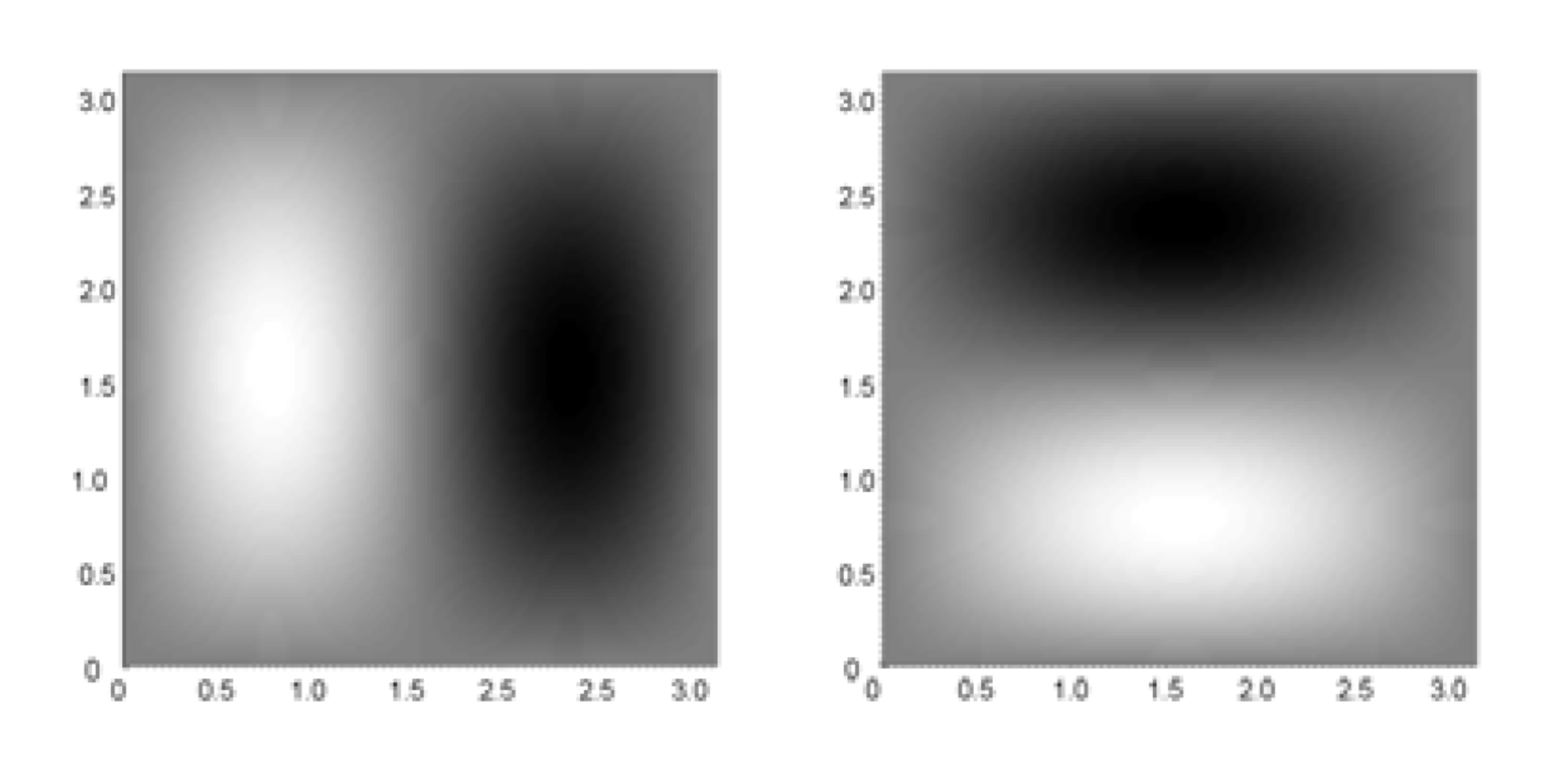
D(x)\nabla_{ \mathbb S^2} u = {\color{red} ρ_1}(\nabla_{ \mathbb S^2} f (x) \cdot \nabla_{ \mathbb S^2} u)\nabla_{ \mathbb S^2} f (x) \\ \qquad+ {\color{blue} \rho_2 }(x \times \nabla_{ \mathbb S^2} f (x) \cdot \nabla_{ \mathbb S^2}u )(x \times \nabla_{ \mathbb S^2} f (x) )

\(\rho_1\) small, \(\rho_2\) large: field is elongated tangentially along level sets of \(f\)

\(\rho_1\) large, \(\rho_2\) small: field is elongated orthogonally along level sets of \(f\)

The Model: Example 3

\mathcal M = \mathbb{S}^2, \gamma(\lambda) = \lambda^{-0.75}
V(x) = 10 \\ f(x) = x_2, \rho_1 = 1, \rho_2 = 25

The Model: Example 3

\mathcal M = \mathbb{S}^2, \gamma(\lambda) = \lambda^{-0.75}

The Model: Example

  • "Preferred directions"
  • "Local activations"
  • "Local correlation length"
  • Different regularity by \(\gamma\)

Non-spherical examples

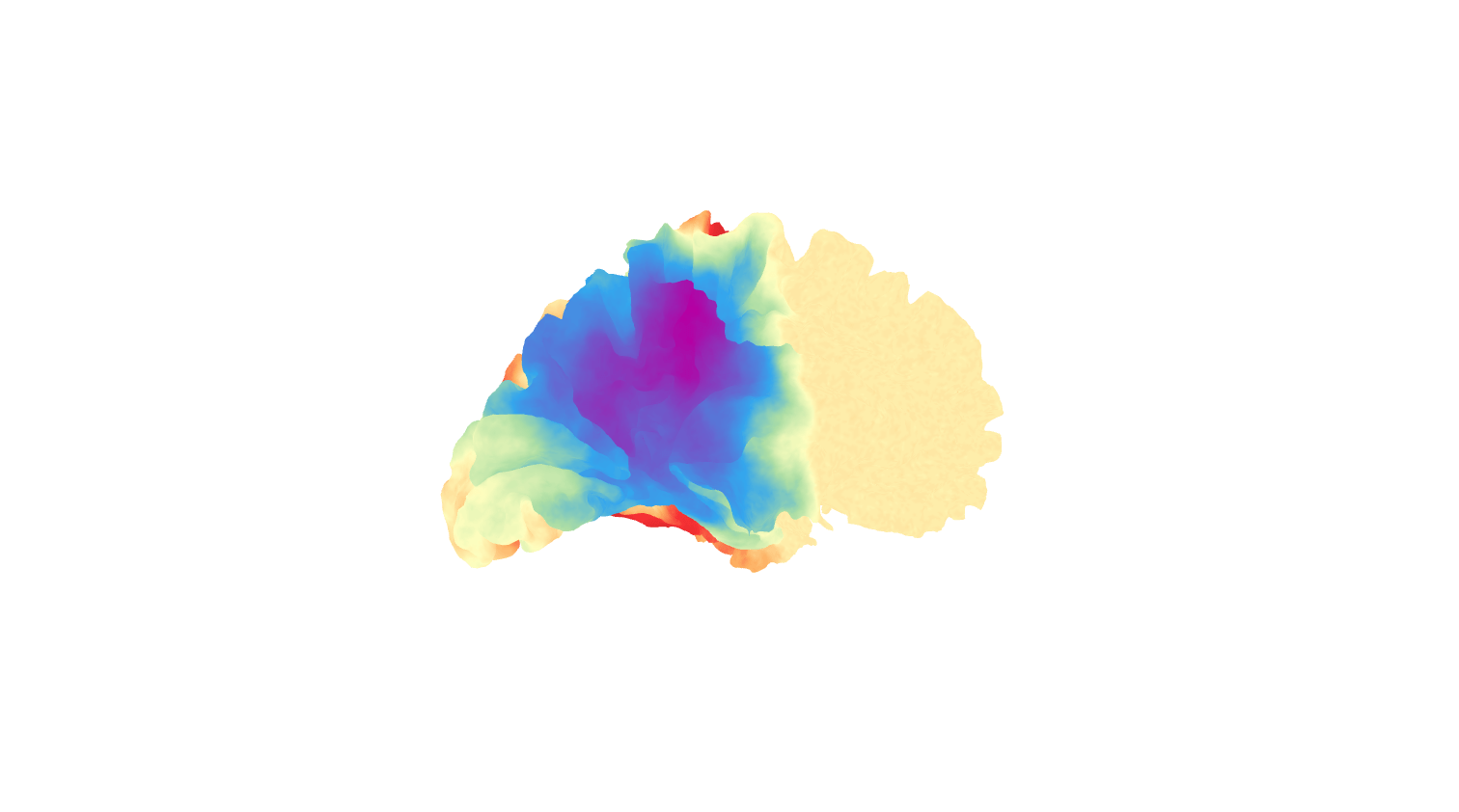
5

Sampling the fields

Problem: \((\lambda_i,e_i)\) is not available!

Sampling \(\iff\) Evaluating \(\mathcal Z = \sum_{i=1}^\infty \gamma(\lambda_i) W_i e_i\)

Can \((\lambda_i,e_i)\) be approximated?

Maybe? Solving an SPDE, try with FEM!

Main computational tool: FEM

On Euclidean spaces

Just triangulate the domain!

\mathcal{D}
\mathcal{D}

Put the pieces back together, get the original domain!

Main computational tool: FEM

On manifolds!

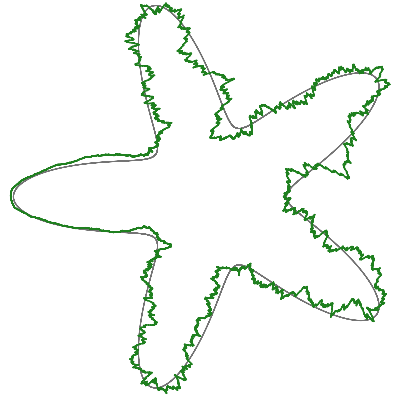
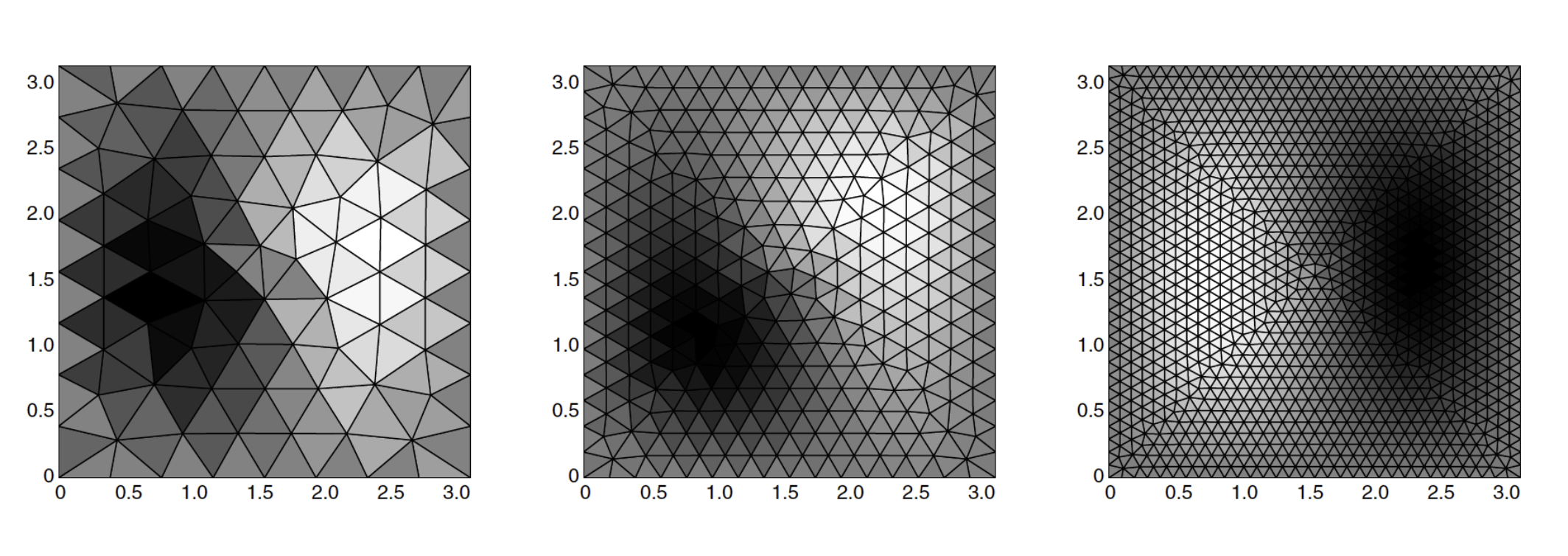
Step 1: Triangulate the domain

\mathcal{M}
\mathcal{M}_h

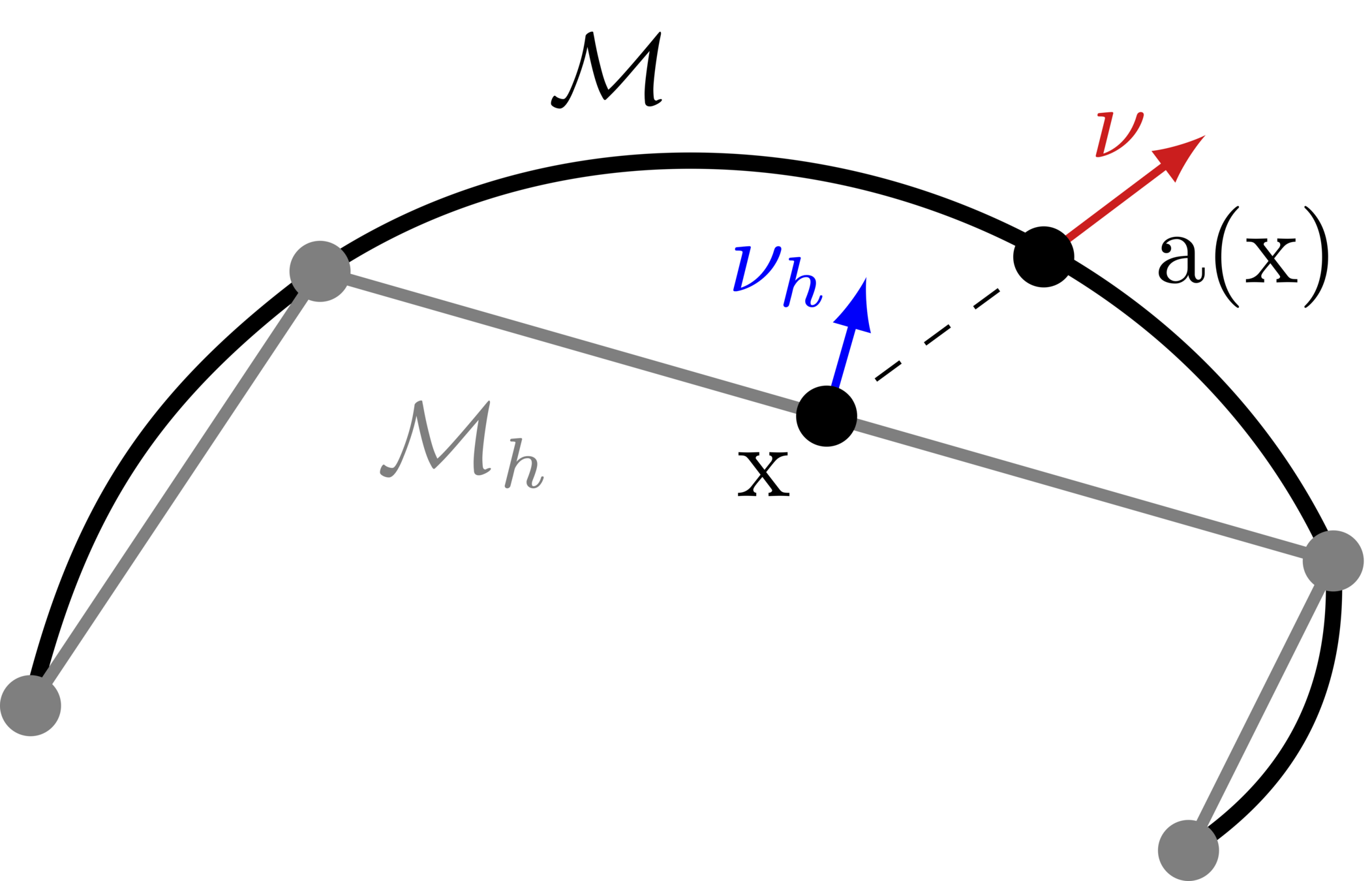
Issue: Approximate solutions live on \(\mathcal{M}_h\), not \(\mathcal{M}\)!

Put the pieces back together, don't get the same domain!

Step 2: FEM space \(S_h \subset H^1(\mathcal{M}_h)\) of p.w., continuous, linear functions

Given \(\eta: \mathcal{M}_h \to \mathbb{R}\), \(\eta^\ell= \eta \circ a\) is on \(\mathcal{M}\)!

Step 3: Key tool in surface finite elements: the lift

Takeway: FEM error similar to flat case, up to a "geometry error" term

Main computational tool: FEM

Main computational tool: FEM

Discretization of operators

\mathcal M, \, H^{1}(\mathcal M)

Original

\mathcal{L}

Eigenpairs

(\lambda_i,e_i)

Discrete 1

\mathcal M, \, S_h^\ell
\mathcal{L}_h

Eigenpairs

(\lambda_{i,h},e_{i,h})

Discrete 2

\mathcal M_h, \, S_h
\mathsf L_h

Eigenpairs

(\Lambda_{i,h},E_{i,h})

How to sample?

\mathcal{Z}=\sum_{i\in\N}\gamma(\lambda_{i})W_ie_i

Use eigenpairs \((\Lambda_{i,h},E_{i,h})\) of \(\mathsf{L}_h\)

First idea: Use these to approximate

\mathcal{Z} \approx \sum_{i=1}^{N_h} \gamma(\Lambda_{i,h})\overline{W}_i E_{i,h}

How to sample?

In practice:

\sum_{i=1}^{N_h} \gamma(\Lambda_{i,h})\overline{W}_i E_{i,h} = \sum_{i=1}^{N_h} Z_i \psi_i

Works with known mesh, "unknown" manifold:

Find a mesh and you can simulate GRFs on it!

What about strong error?

\((Z_i)\) are Gaussian with covariance matrix determined by \(\gamma\) and FEM matrices

How to sample, really?

Z \sim N(0,\Sigma_Z)
\Sigma_Z = \sqrt{C}^{-T} \gamma^2(S) \sqrt{C}
C_{kl} = (\psi_k,\psi_l)_{L^2(\mathcal M_h)}
R_{kl} = \mathsf{A}_{\mathcal M_h}(\psi_k,\psi_l)
S = \sqrt{C}^{-1} R \sqrt{C}^{-T}

Chebyshev quadrature approximation of \(\gamma\)

Error analysis: first try

First try:

Problem:

\sum_{i\in\N}\gamma(\lambda_{i})W_ie_i - \sum_{i=1}^{N_h} \gamma(\Lambda_{i,h})\overline{W}_i E_{i,h}
\|e_i-E_{i,h}\|_{L^2} ??

Generally: Approximating eigenfunctions are hard!

Eigenvalues are fine, however!

Problematic discrete eigenfunctions

Generally: Approximating eigenfunctions are hard! Multiplicity!

From D. Boffi, Acta Num. (2010)

Noise and Field Approximations

Various white noise approximations, various approximations of \(\mathcal Z\)

\widetilde{\mathcal W} = P_h \mathcal W \, (\in S_h^\ell)
\widetilde{\mathcal Z}_h = \gamma(\mathcal L_h )P_h \mathcal W
\hat{\mathsf{W}} = \mathsf P_h (\sigma \widetilde{\mathcal{W}}^{-\ell})
\mathsf W = \mathsf P_h (\sigma^{1/2} \widetilde{\mathcal{W}}^{-\ell})
\hat{\mathsf{Z}}_h = \gamma(\mathsf L_h )\hat{\mathsf W}
\mathsf{Z}_h = \gamma(\mathsf L_h )\mathsf W

sd

 

 

 

sd

 

 

 

sd

 

 

 

\mathsf{Z}_h = \sum_{i=1}^{N_h} \gamma(\Lambda_{i,h})\overline{W}_i E_{i,h}

Strong error roadmap

\widetilde{\mathcal Z} = \gamma(\mathcal L ) \mathcal W
\hat{\mathsf{Z}}_h = \gamma(\mathsf L_h )\hat{\mathsf W}
\mathsf{Z}_h = \gamma(\mathsf L_h )\mathsf W
\widetilde{\mathcal Z}_h = \gamma(\mathcal L_h )P_h \mathcal W

??

Important result: errors on the form

\(\|\gamma(\mathcal L)f -\gamma(\mathcal L_h) f\|_{L^2}\)

Brief note on proof:

\gamma(\mathcal L) f = \frac{1}{2\pi i } \int_{\Gamma} \gamma(z)(z-\mathcal{L})^{-1}f \\ \gamma(\mathcal L_h) f = \frac{1}{2\pi i } \int_{\Gamma} \gamma(z)(z-\mathcal{L}_h)^{-1}f

Deterministic Error Result

Brief note on proof:

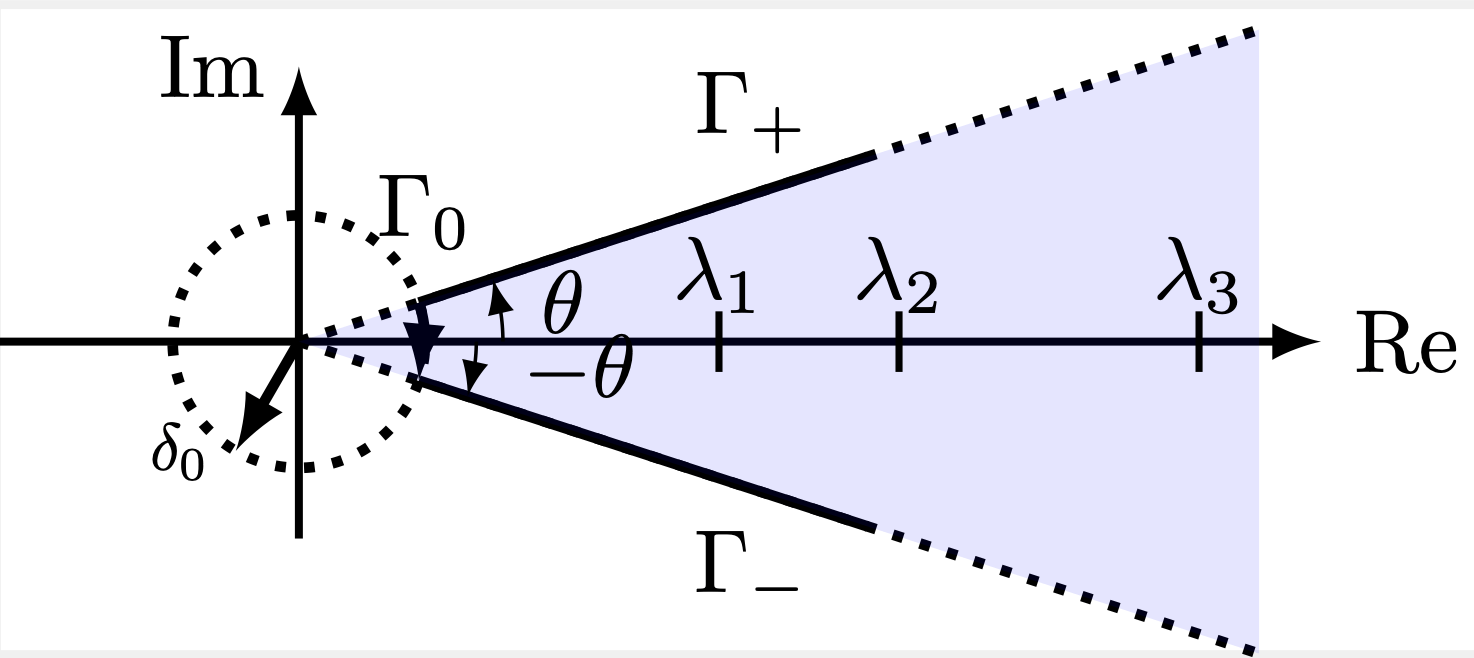
\gamma(\mathcal L) f = \frac{1}{2\pi i } \int_{\Gamma} \gamma(z)(z-\mathcal{L})^{-1}f \\ \gamma(\mathcal L_h) f = \frac{1}{2\pi i } \int_{\Gamma} \gamma(z)(z-\mathcal{L}_h)^{-1}f

Deterministic Error Result

Strong error bound

In the end:

\|\mathcal Z - \mathsf Z_h^\ell\|_{L^2} \lesssim K_\alpha(h) h^{2\min\{\alpha -d/4; 1\}} \\ K_\alpha(h) = \begin{cases} |\log h| ~\text{ if } d/4 < \alpha \leq 1 \\ |\log h|^{3/2} \text{ if } 1<\alpha <1+d/2 \\ |\log h|^{1/2} \text{ else }\end{cases}

Mandatory error simulation plots

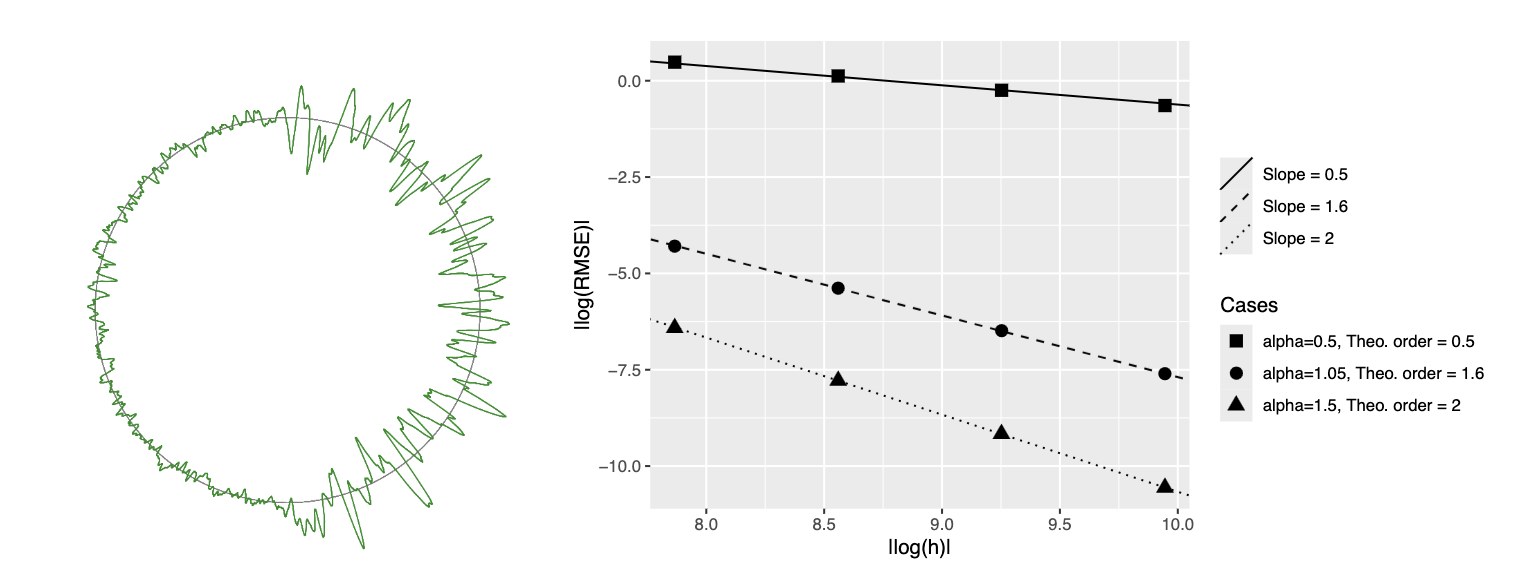
\(\alpha = 1.75\)

\gamma(\lambda) = V_0^\alpha (\lambda + \cos(0.9\pi)\sqrt{\lambda})^{-\alpha} \\ \mathcal D(x) = I-xx^T \\ V(x) = 3V_0 \text{ if $\theta \in (\pi/2,3\pi/2)$}, V_0 \text{ else}

Mandatory error simulation plots

Mandatory error simulation plots

\(\alpha = 1.75\)

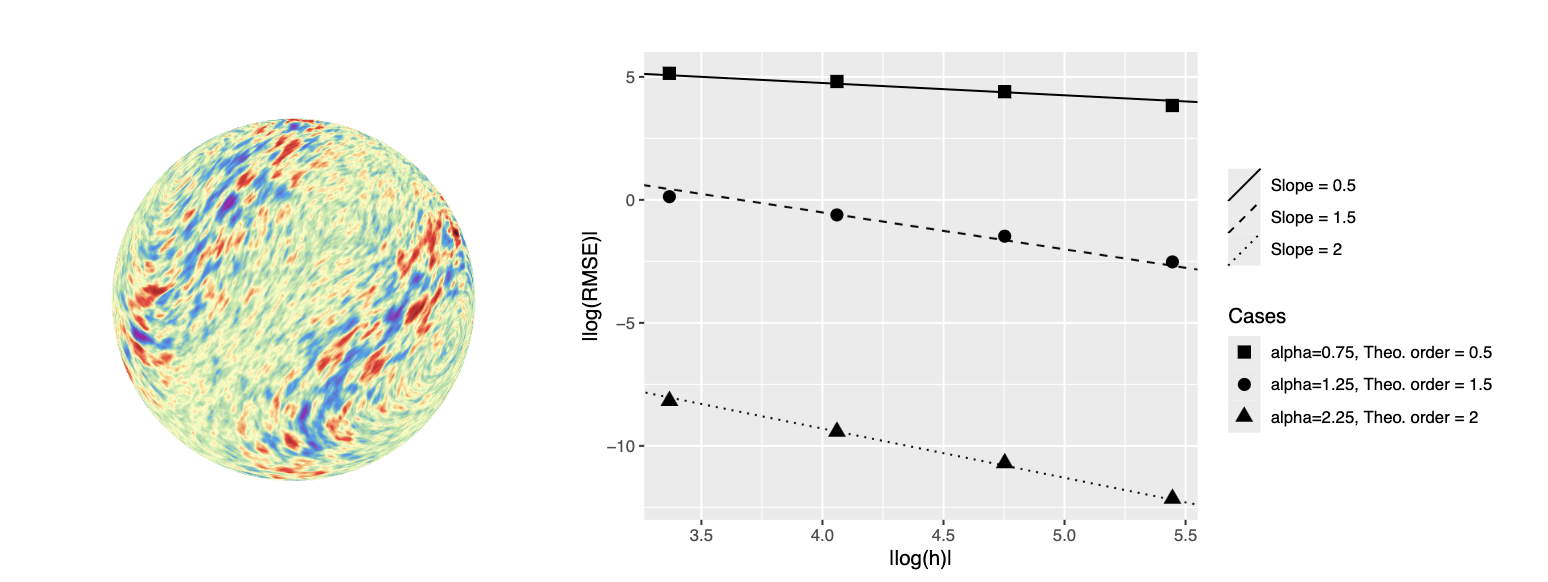
\gamma(\lambda) = C_0 \lambda^{-\alpha} \\ \mathcal D(x) = \nabla_M f(x)(\nabla_M f(x))^T + \rho(x)\nabla^\perp_M f(x)(\nabla^\perp_M f(x))^T \\ f(x) = 2\cos(\theta(x)) \cos(\phi(x)) \sin^2(\theta(x)), \rho(x) = 0.1 + 0.6/(1 + e^{−4\cos(\theta(x))}) \\ V(x) = 500(1 +5 \cos^2(\pi\theta(x)))

In conclusion...

  • We can sample non-stationary random fields on curves and surfaces using mesh only
  • We can prove that the strong error is bounded
  • Time dependence: soon on a preprint server
  • Inference: Discuss?