data science
for (physical) scientists 9
dr.federica bianco | fbb.space | fedhere | fedhere


Clustering
this slide deck:
-
Machine Learning basic concepts
- parameters vs hyperparameters
- supervised/unsupervised
- Clustering : how it works
-
Partitioning
- Hard clustering
- Soft Clustering
- Density based
-
Hirarchical
- agglomerative
- devisive
-
also:
- Grid based
- Model based
recap
what is machine learning
what is machine learning?
classification
prediction
feature selection
supervised learning
understanding structure
organizing/compressing data
anomaly detection dimensionality reduction
unsupervised learning
general ML points
general ML points
understand structure of feature space
prediction based on examples (inferential AI)
generate new instances (generative AI)
=> second order purpose | feature importance
what is machine good for?
what is machine learning?
[Machine Learning is the] field of study that gives computers the ability to learn without being explicitly programmed. Arthur Samuel, 1959
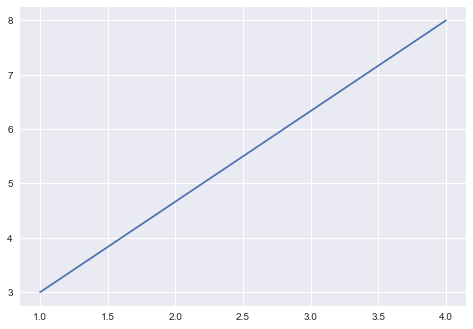
model
parameters:
slope, intercept
data
ML: any model with parameters learnt from the data
what is machine learning?
[Machine Learning is the] field of study that gives computers the ability to learn without being explicitly programmed. Arthur Samuel, 1959

model
parameters:
slope, intercept

data
ML: any model with parameters learnt from the data
Via minimization of a loss function
what is machine learning?
Loss function is "distance" between known and predicted values of the target variable
supervised learning
????
unsupervised learning
general ML points
general ML points
why
understand structure of feature space
- dimensionality reduction
- anomaly detection
what is machine good for?
(e.g. image compression)
general ML points
should be interpretable:
why?
predictive policing,
selection of conference participants.
ethical implications
general ML points
should be interpretable:
prective policing,
selection of conference participants.
why the model made a choice?
which feature mattered?
why?
ethical implications
causal connection
general ML points
should be interpretable:

ethical implications
general ML points
ML model have parameters and hyperparameters
parameters: the model optimizes based on the data
hyperparameters: chosen by the model author, could be based on domain knowledge, other data, guessed (?!).
e.g. the shape of the polynomial
1
clustering
observed features:
(x, y)
GOAL: partitioning data in maximally homogeneous,
maximally distinguished subsets.
clustering is an unsupervised learning method
x
y
all features are observed for all objects in the sample
(x, y)
how should I group the observations in this feature space?
e.g.: how many groups should I make?
clustering is an unsupervised learning method
x
y
optimal
clustering

internal criterion:
members of the cluster should be similar to each other (intra cluster compactness)
external criterion:
objects outside the cluster should be dissimilar from the objects inside the cluster

tigers
wales
raptors
zoologist's clusters
orange/green
black/white/blue


internal criterion:
members of the cluster should be similar to each other (intra cluster compactness)
external criterion:
objects outside the cluster should be dissimilar from the objects inside the cluster
photographer's clusters
the optimal clustering depends on:
-
how you define similarity/distance
- the purpose of the clustering
internal criterion:
members of the cluster should be similar to each other (intra cluster compactness)
external criterion:
objects outside the cluster should be dissimilar from the objects inside the cluster
the ideal clustering algorithm should have:
-
Scalability (naive algorithms are Np hard)
-
Ability to deal with different types of attributes
-
Discovery of clusters with arbitrary shapes
-
Minimal requirement for domain knowledge
-
Deals with noise and outliers
-
Insensitive to order
-
Allows incorporation of constraints
-
Interpretable
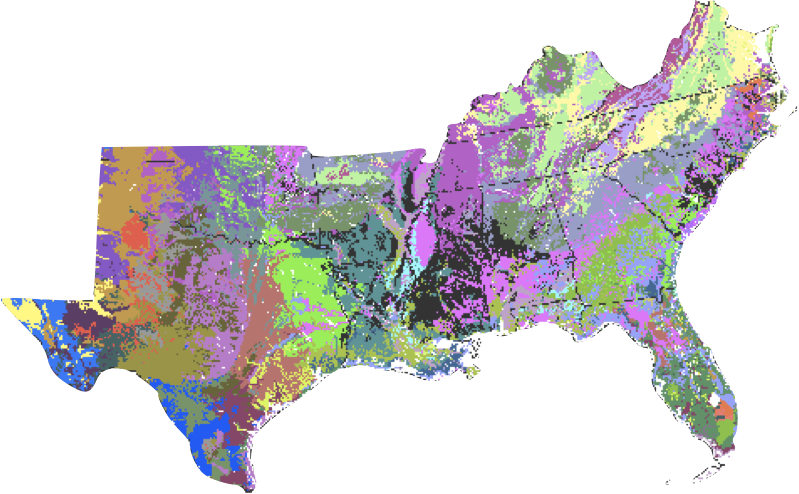
A Spatial Clustering Technique for the Identification of Customizable Ecoregions
William W. Hargrove and Robert J. Luxmoore
thinking about distances spatially helps intuition
but exercise in abstracting these distances to non-spatial features

A Spatial Clustering Technique for the Identification of Customizable Ecoregions
William W. Hargrove and Robert J. Luxmoore
50-year mean monthly temperature, 50-year mean monthly precipitation, elevation, total plant-available water content of soil, total organic matter in soil, and total Kjeldahl soil nitrogen
2
distance metrics
distance metrics
continuous variables
Minkowski family of distances
distance metrics
continuous variables
Minkowski family of distances
N features (dimensions)
i,j objects
distance metrics
continuous variables
Minkowski family of distances
N features (dimensions)
properties:
distance metrics
continuous variables
Minkowski family of distances
Manhattan: p=1
features: x, y
distance metrics
continuous variables
Minkowski family of distances

Manhattan: p=1
features: x, y
distance metrics
continuous variables
Minkowski family of distances

Euclidean: p=2
features: x, y
distance metrics
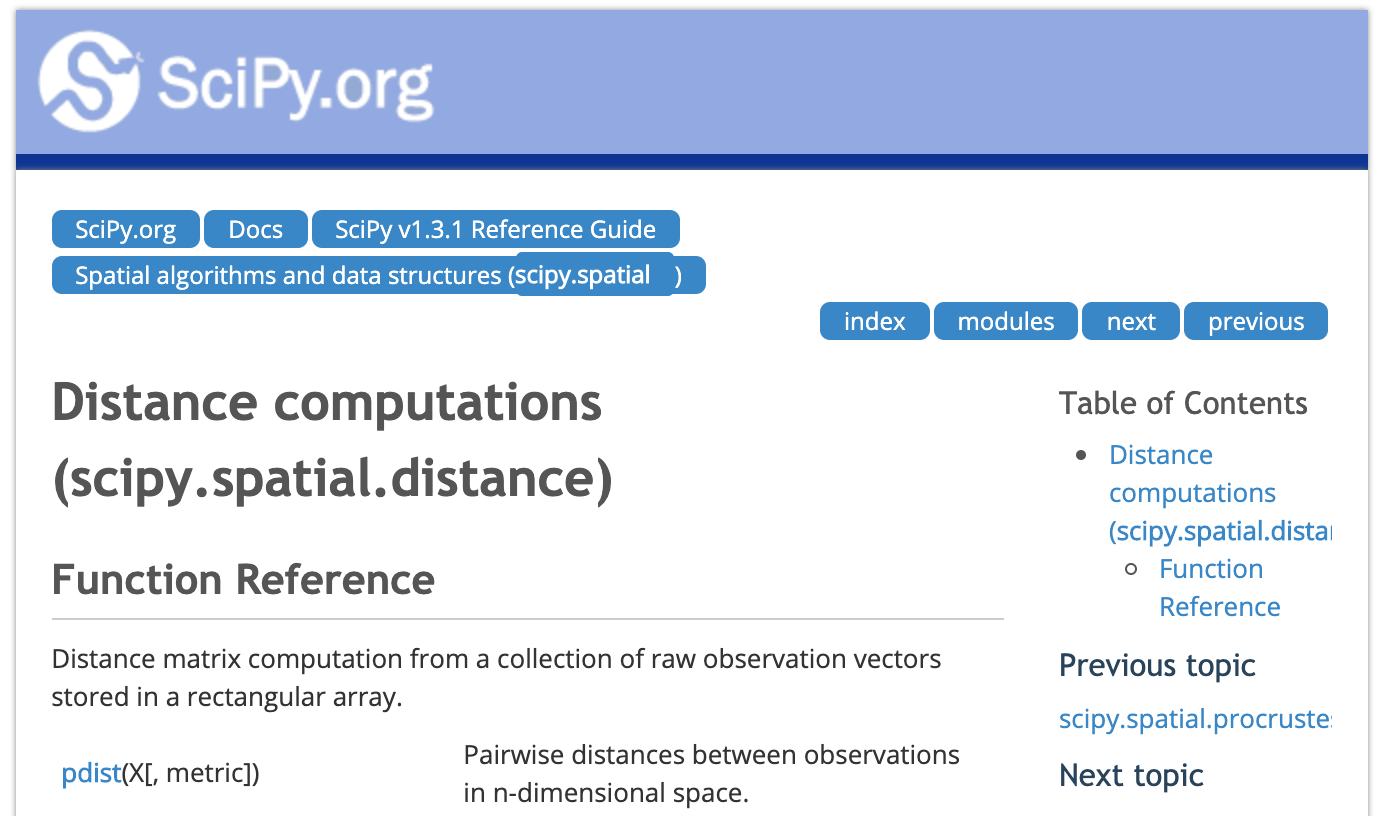


import scipy as sp
sp.spatial.distance.pdist(X) # the pairwise distance: returns (N**2 - N )/2 values for N objects
sp.spatial.distance.squareform(sp.spatial.distance.pdist(wines[["Alcohol", "Magnesium"]]))
#returns the NXN matrix of distances
plt.imshow(sp.spatial.distance.squareform(sp.spatial.distance.pdist(wines[["Alcohol", "Magnesium"]])))
#you can visualize the NXN matrix
plt.xlabel("wine")
plt.ylabel("wine");
plt.colorbar(label="distance");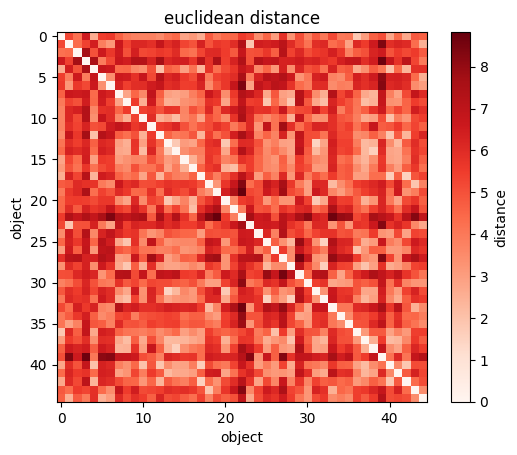
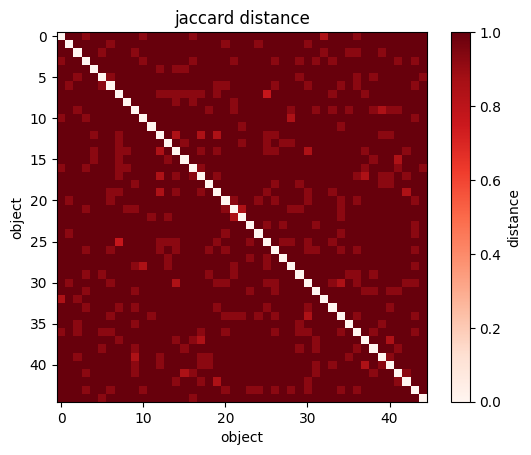
import scipy as sp
sp.spatial.distance.pdist(X) # the pairwise distance: returns (N**2 - N )/2 values for N objects
sp.spatial.distance.squareform(sp.spatial.distance.pdist(wines[["Alcohol", "Magnesium"]],
metric='jaccard'))
#returns the NXN matrix of distances
plt.imshow(sp.spatial.distance.squareform(sp.spatial.distance.pdist(wines[["Alcohol", "Magnesium"]])))
#you can visualize the NXN matrix
plt.xlabel("wine")
plt.ylabel("wine");
plt.colorbar(label="distance");
distance metrics
Minkowski family of distances
Great Circle distance
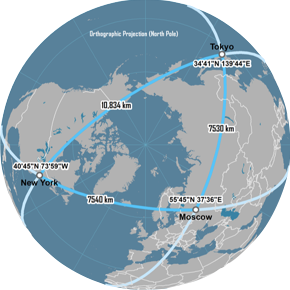
features
latitude and longitude
continuous variables
#Great Circle Distance in the sky
import astropy.units as u
from astropy.coordinates import SkyCoord
#The on-sky separation can be computed with the astropy.coordinates.BaseCoordinateFrame.separation()
#or astropy.coordinates.SkyCoord.separation() methods,
#which computes the great-circle distance (not the small-angle approximation):
c1 = SkyCoord('5h23m34.5s', '-69d45m22s', frame='icrs')
c2 = SkyCoord('0h52m44.8s', '-72d49m43s', frame='fk5')
sep = c1.separation(c2)Angle 20.74611448 deg
from shapely.geometry import Point
import geopandas as gpd
pnt1 = Point(80.99456, 7.86795)
pnt2 = Point(80.97454, 7.872174)
points_df = gpd.GeoDataFrame({'geometry': [pnt1, pnt2]}, crs='EPSG:4326')
points_df = points_df.to_crs('EPSG:5234')
points_df2 = points_df.shift() #We shift the dataframe by 1 to align pnt1 with pnt2
points_df.distance(points_df2)https://www.codedrome.com/calculating-great-circle-distances-in-python/
https://pypi.org/project/great-circle-calculator/
from math import radians, degrees, sin, cos, asin, acos, sqrt
def great_circle(lon1, lat1, lon2, lat2):
lon1, lat1, lon2, lat2 = map(radians, [lon1, lat1, lon2, lat2])
return 6371 * (acos(sin(lat1) * sin(lat2) + cos(lat1) *
cos(lat2) * cos(lon1 - lon2))) #kmdistance metrics
Uses presence/absence of features in data
: number of features in neither
: number of features in both
: number of features in i but not j
: number of features in j but not i
categorical variables:
binary
What is the distance between a leopard and a lizard?
- they both have tails
- only lizards have scales
- neither have wings


distance metrics
Uses presence/absence of features in data
: number of features in neither
: number of features in both
: number of features in i but not j
: number of features in j but not i
categorical variables:
binary
What is the distance between a leopard and a lizard?
- they both have tails
- only lizards have scales
- neither have wings
distance metrics
| 1 | 0 | sum | |
|---|---|---|---|
| 1 | M11 | M10 | M11+M10 |
| 0 | M01 | M00 | M01+M00 |
| sum | M11+M01 | M10+M00 | M11+M00+M01+ M10 |
observation i
}
}
| 0 | sum | ||
|---|---|---|---|
| 1 | M10 | M11+M10 | |
| 0 | M01 | M00 | M01+M00 |
| sum | M11+M01 | M10+M00 | M11+M00+M01+ M10 |
1
1
1
0
observation j
distance metrics
Uses presence/absence of features in data
: number of features in neither
: number of features in both
: number of features in i but not j
: number of features in j but not i
categorical variables:
binary
What is the distance between a leopard and a lizard?
- they both have tails
- only lizards have scales
- neither have wings
distance metrics
| 1 | 0 | sum | |
|---|---|---|---|
| 1 | M11 | M10 | M11+M10 |
| 0 | M01 | M00 | M01+M00 |
| sum | M11+M01 | M10+M00 | M11+M00+M01+ M10 |
observation i
}
}
| 0 | sum | ||
|---|---|---|---|
| 1 | M10 | M11+M10 | |
| 0 | M01 | M00 | M01+M00 |
| sum | M11+M01 | M10+M00 | M11+M00+M01+ M10 |
observation j
distance metrics
Simple Matching Distance
Uses presence/absence of features in data
: number of features in neither
: number of features in both
: number of features in i but not j
: number of features in j but not i
Simple Matching Coefficient
or Rand similarity
| 1 | 0 | sum | |
|---|---|---|---|
| 1 | M11 | M10 | M11+M10 |
| 0 | M01 | M00 | M01+M00 |
| sum | M11+M01 | M10+M00 | M11+M00+M01+ M10 |
observation i
observation j
}
}
categorical variables:
binary
| 0 | sum | ||
|---|---|---|---|
| 1 | M11 | M10 | M11+M10 |
| 0 | M01 | M00 | M01+M00 |
| sum | M11+M01 | M10+M00 | M11+M00+M01+ M10 |
lizard/leopard
1
1
1
0
distance metrics
Jaccard similarity
Jaccard distance
| 1 | 0 | sum | |
|---|---|---|---|
| 1 | M11 | M10 | M11+M10 |
| 0 | M01 | M00 | M01+M00 |
| sum | M11+M01 | M10+M00 | M11+M00+M01+ M10 |
observation i
observation j
}
}
categorical variables:
binary
lizard/leopard
distance metrics
Jaccard similarity
Jaccard distance
| 1 | 0 | sum | |
|---|---|---|---|
| 1 | M11 | M10 | M11+M10 |
| 0 | M01 | M00 | M01+M00 |
| sum | M11+M01 | M10+M00 | M11+M00+M01+ M10 |
observation i
observation j
}
}
categorical variables:
binary
distance metrics
Jaccard similarity
Application to Deep Learning for image recognition
Convolutional Neural Nets
categorical variables:
binary
3
whitening
Data can have covariance (and it almost always does!)
PLUTO Manhattan data (42,000 x 15)
axis 1 -> features
axis 0 -> observations
Data can have covariance (and it almost always does!)
Data can have covariance (and it almost always does!)
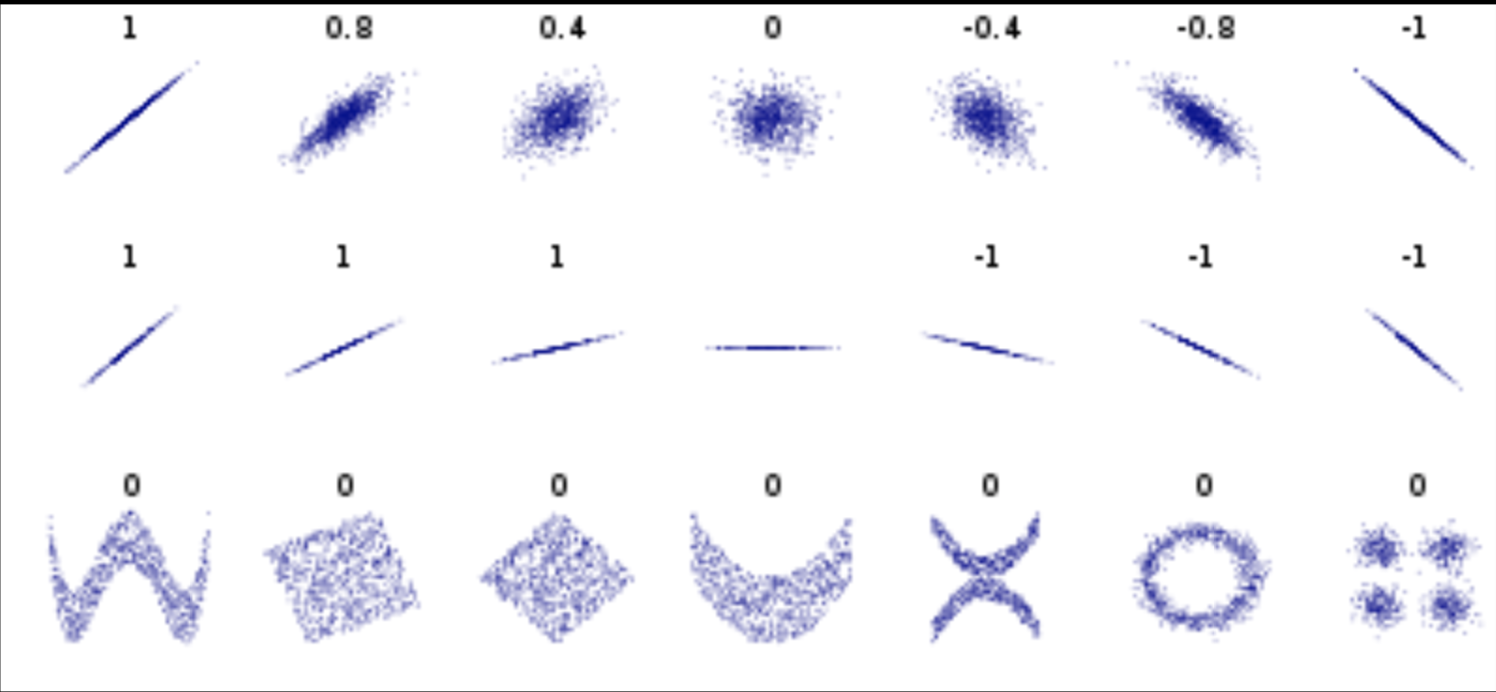
Pearson's correlation (linear correlation)
correlation = correlation / variance
PLUTO Manhattan data (42,000 x 15) correlation matrix
axis 1 -> features
axis 0 -> observations
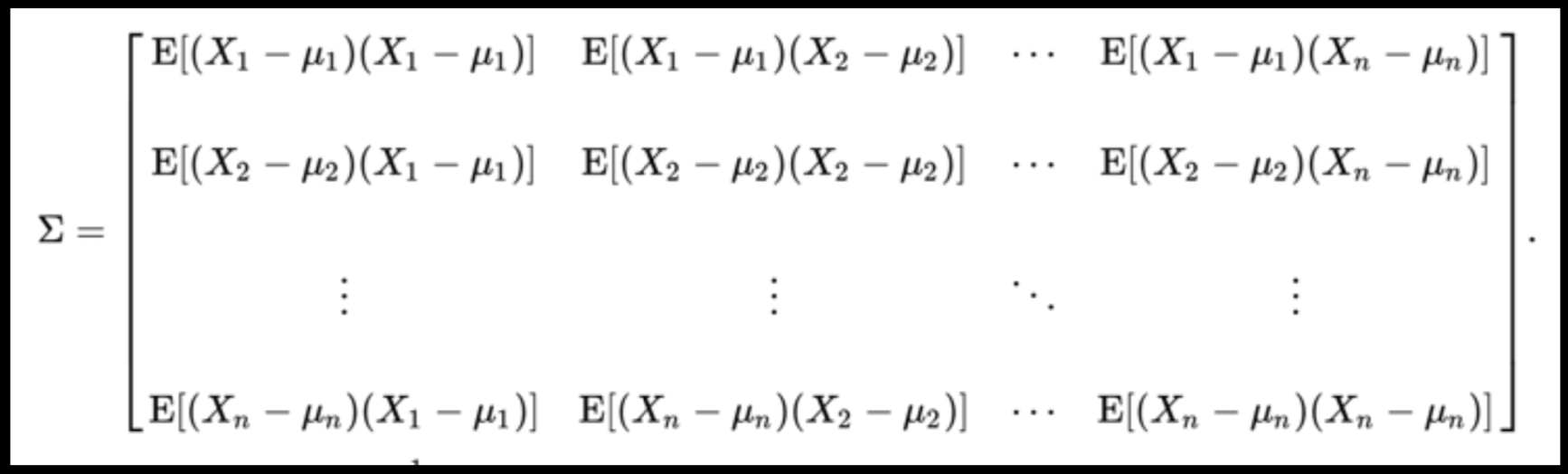
Data can have covariance (and it almost always does!)
PLUTO Manhattan data (42,000 x 15) correlation matrix
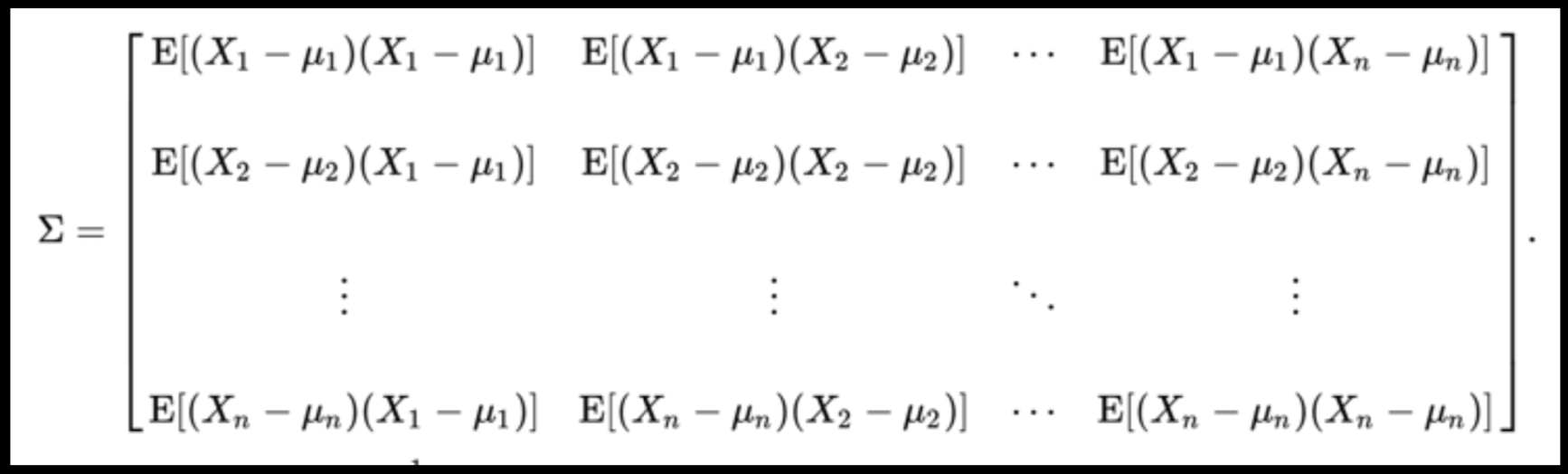

A covariance matrix is diagonal if the data has no correlation
Data can have covariance (and it almost always does!)
Full On Whitening
find the matrix W that diagonalized Σ
from zca import ZCA import numpy as np
X = np.random.random((10000, 15)) # data array
trf = ZCA().fit(X)
X_whitened = trf.transform(X)
X_reconstructed =
trf.inverse_transform(X_whitened)
assert(np.allclose(X, X_reconstructed))
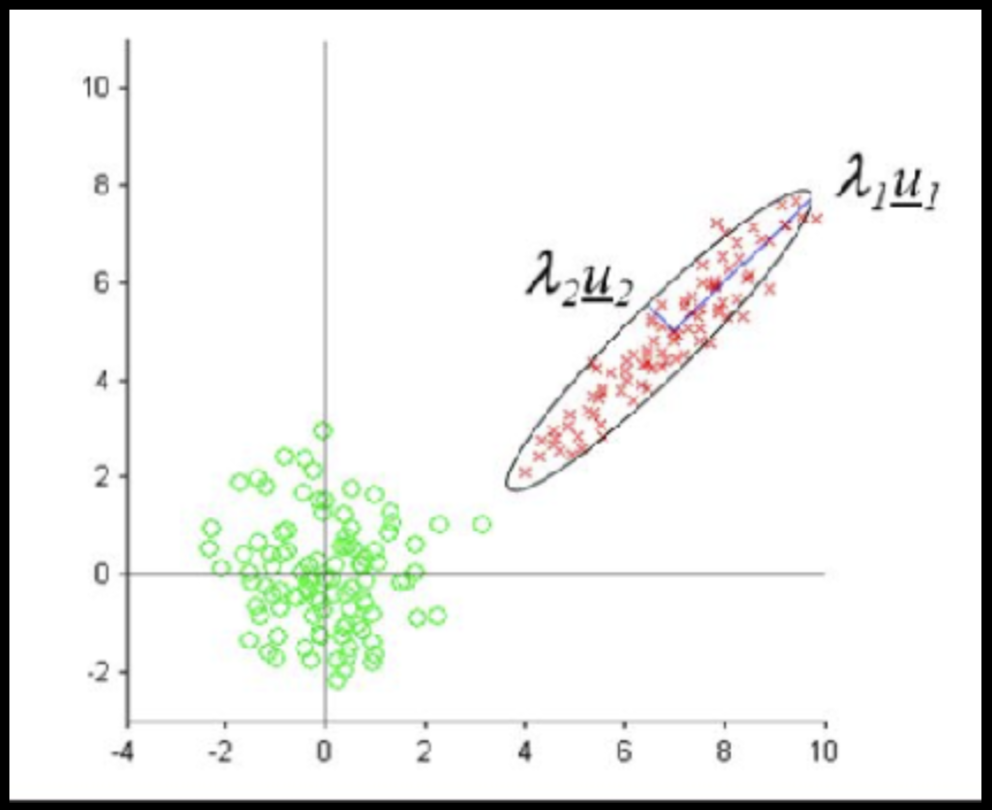
: remove covariance by diagonalizing the transforming the data with a matrix that diagonalizes the covariance matrix
this is at best hard, in some cases impossible even numerically on large datasets
Data that is not correlated appear as a sphere in the Ndimensional feature space
Data can have covariance (and it almost always does!)
ORIGINAL DATA
STANDARDIZED DATA
Generic preprocessing
Generic preprocessing
for each feature: divide by standard deviation and subtract mean
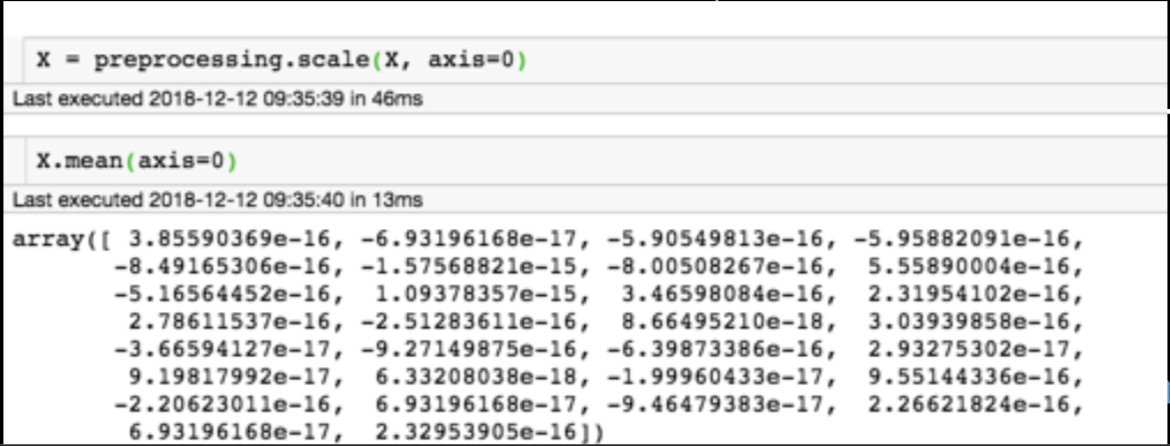

mean of each feature should be 0, standard deviation of each feature should be 1

4
how clustring works
-
Partitioning
- Hard clustering
- Soft Clustering
-
Hirarchical
- agglomerative
- devisive
-
also:
- Density based
- Grid based
- Model based
K-means (McQueen ’67)
K-medoids (Kaufman & Rausseeuw ’87)
Expectation Maximization (Dempster,Laird,Rubin ’77)
5
clustering by
partitioning
5.1
k-means:
Hard partitioning cluster method
K-means: the algorithm
Choose N “centers” guesses: random points in the feature space repeat: Calculate distance between each point and each center Assign each point to the closest center Calculate the new cluster centers untill (convergence): when clusters no longer change
K-means: the algorithm
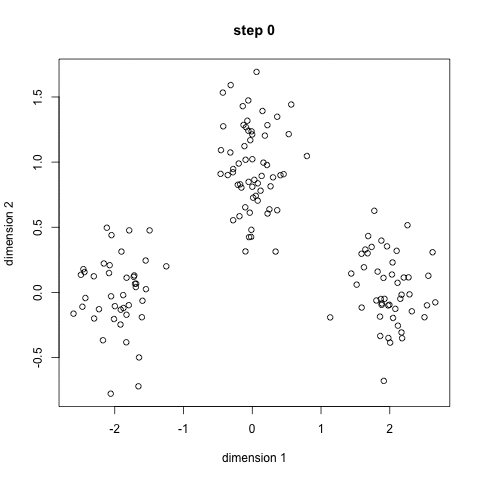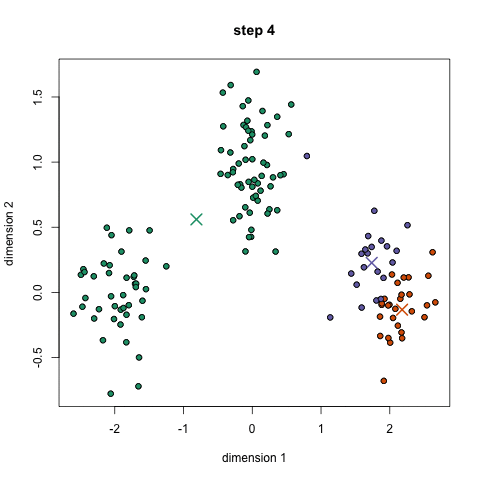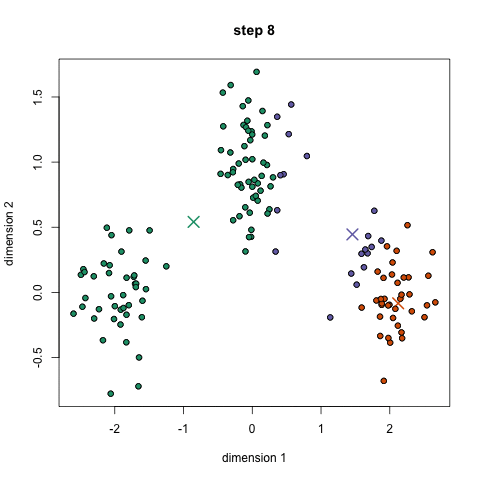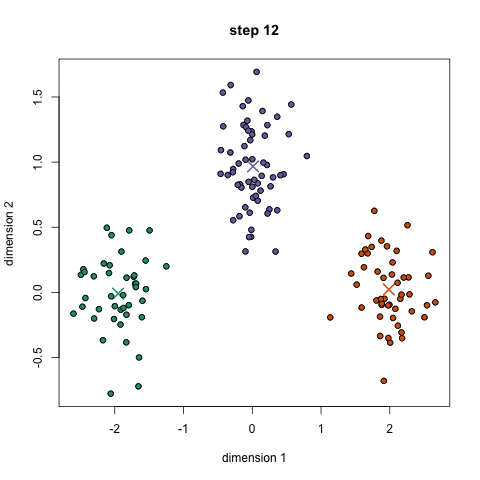
K-means:
Objective: minimizing the aggregate distance within the cluster.
Order: #clusters #dimensions #iterations #datapoints O(KdN)
CONs:
Its non-deterministic: the result depends on the (random) starting point
It only works where the mean is defined: alternative is K-medoids which represents the cluster by its central member (median), rather than by the mean
Must declare the number of clusters upfront (how would you know it?)
PROs:
Scales linearly with d and N
K-means: the objective function
Objective: minimizing the aggregate distance within the cluster.
Order: #clusters #dimensions #iterations #datapoints O(KdN)
O(KdN):
complexity scales linearly with
-d number of dimensions
-N number of datapoints
-K number of clusters
K-means: the objective function
either you know it because of domain knowledge
or
you choose it after the fact: "elbow method"
total intra-cluster variance
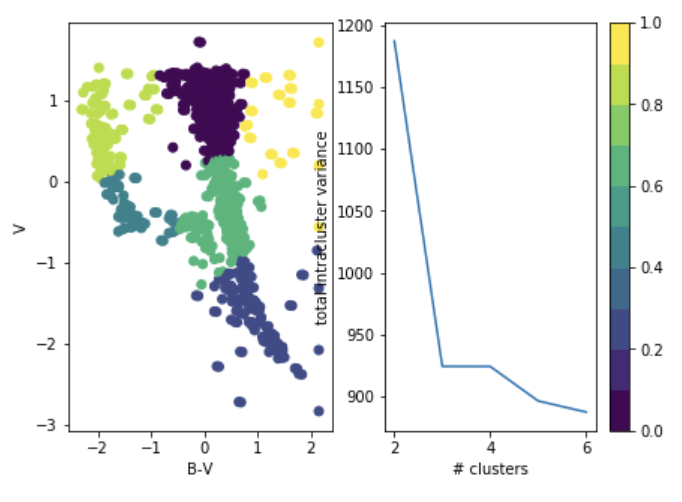
Objective: minimizing the aggregate distance within the cluster.
Order: #clusters #dimensions #iterations #datapoints O(KdN)
Must declare the number of clusters
K-means: the objective function
Objective: minimizing the aggregate distance within the cluster.
Order: #clusters #dimensions #iterations #datapoints O(KdN)
Must declare the number of clusters upfront (how would you know it?)
either domain knowledge or
after the fact: "elbow method"
total intra-cluster variance
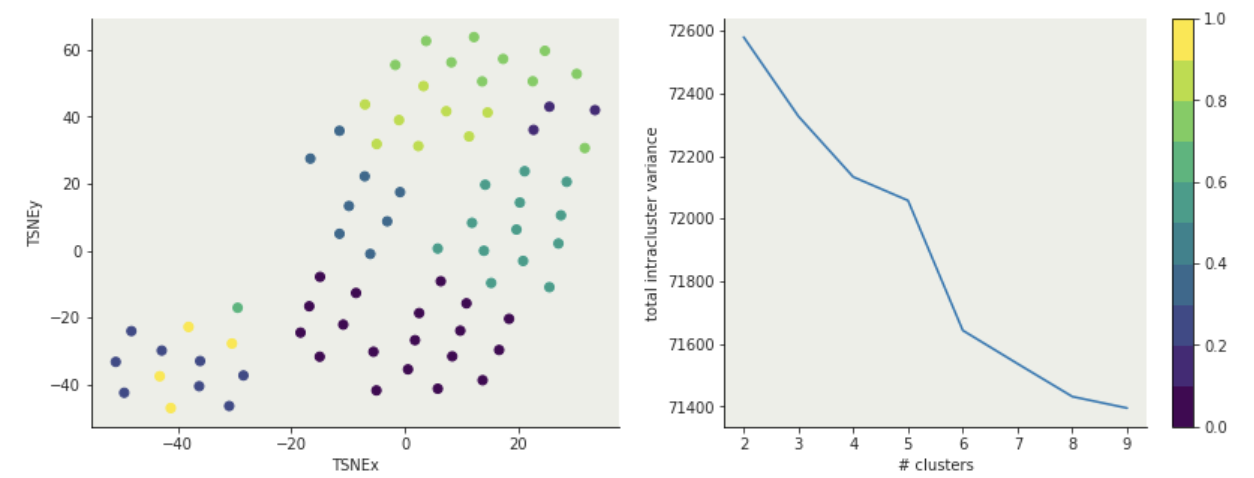
K-means: hyperparameters

- n_clusters : number of clusters
-
init : the initial centers or a scheme to choose the center
‘k-means++’ : selects initial cluster centers for k-mean clustering in a smart way to speed up convergence. See section Notes in k_init for more details.
‘random’: choose k observations (rows) at random from data for the initial centroids.
If an ndarray is passed, it should be of shape (n_clusters, n_features) and gives the initial centers.
- n_init : if >1 it is effectively an ensamble method: runs n times with different initializations
- random_state : for reproducibility
5.2
expectation-maximization
Soft partitioning cluster method
Hard clustering : each object in the sample belongs to only 1 cluster
Soft clustering : to each object in the sample we assign a degree of belief that it belongs to a cluster
Soft = probabilistic
Mixture models
these points come from 2 gaussian distribution.
which point comes from which gaussian?
1
2
3
4-6
7
8
9-12
13

Mixture models
CASE 1:
if i know which point comes from which gaussian
i can solve for the parameters of the gaussian
(e.g. maximizing likelihood)
1
2
3
4-6
7
8
9-12
13
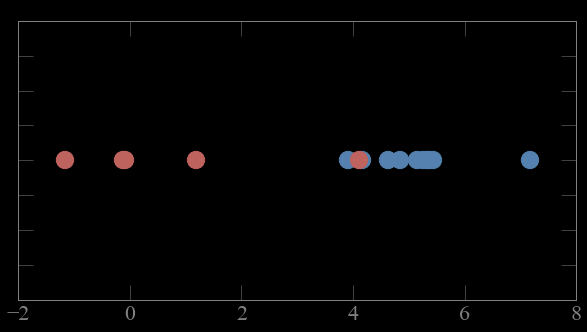
Mixture models
CASE 2:
if i know which the parameters (μ,σ) of the gaussians
i can figure out which gaussian each point is most likely to come from (calculate probability)
1
2
3
4-6
7
8
9-12
13
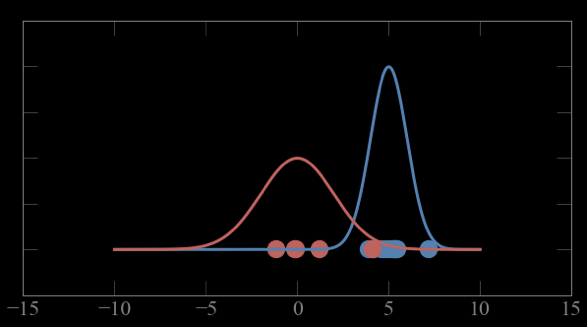

Mixture models:
Guess parameters g= (μ,σ) for 2 Gaussian distributions A and B
calculate the probability of each point to belong to A and B
Expectation maximization

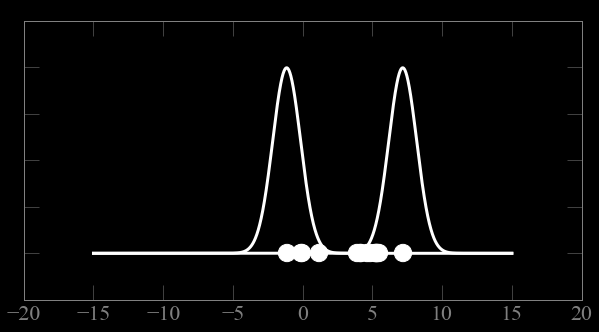
Mixture models:
Guess parameters g= (μ,σ) for 2 Gaussian distributions A and B
calculate the probability of each point to belong to A and B
Expectation maximization


high

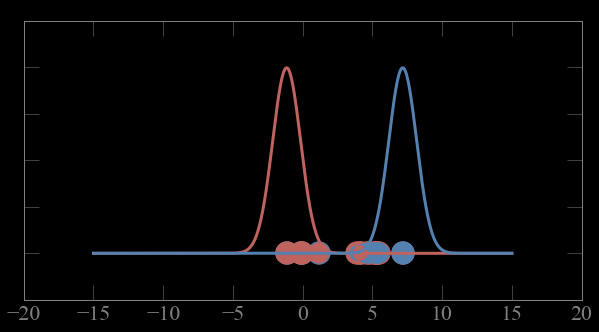
Mixture models:
Expectation maximization

low
Guess parameters g= (μ,σ) for 2 Gaussian distributions A and B
calculate the probability of each point to belong to A and B

Mixture models:
Guess parameters g= (μ,σ) for 2 Gaussian distributions A and B
1- calculate the probability p_ji of each point to belong to gaussian j
Expectation maximization
Bayes theorem: P(A|B) = P(B|A) P(A) / P(B)
Mixture models:
Guess parameters g= (μ,σ) for 2 Gaussian distributions A and B
1- calculate the probability p_ji of each point to belong to gaussian j
2a - calculate the weighted mean of the cluster, weighted by the p_ji
Expectation maximization

Bayes theorem: P(A|B) = P(B|A) P(A) / P(B)
Mixture models:
Expectation maximization

Bayes theorem: P(A|B) = P(B|A) P(A) / P(B)
Guess parameters g= (μ,σ) for 2 Gaussian distributions A and B
1- calculate the probability p_ji of each point to belong to gaussian j
2a - calculate the weighted mean of the cluster, weighted by the p_ji
2b - calculate the weighted sigma of the cluster, weighted by the p_ji
Mixture models:
Expectation maximization

Bayes theorem: P(A|B) = P(B|A) P(A) / P(B)
Alternate expectation and maximization step till convergence
1- calculate the probability p_ji of each point to belong to gaussian j
2a - calculate the weighted mean of the cluster, weighted by the p_ji
2b - calculate the weighted sigma of the cluster, weighted by the p_ji
expectation step
maximization step
}
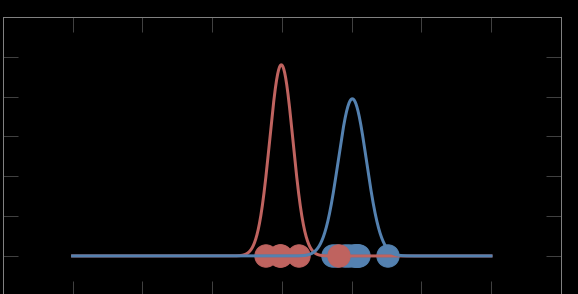
Last iteration: convergence
Mixture models:
Expectation maximization

Bayes theorem: P(A|B) = P(B|A) P(A) / P(B)
Alternate expectation and maximization step till convergence
1- calculate the probability p_ji of each point to belong to gaussian j
2a - calculate the weighted mean of the cluster, weighted by the p_ji
2b - calculate the weighted sigma of the cluster, weighted by the p_ji
expectation step
maximization step
}
EM: the algorithm
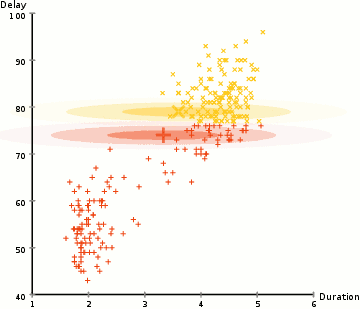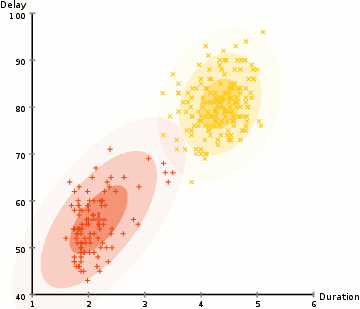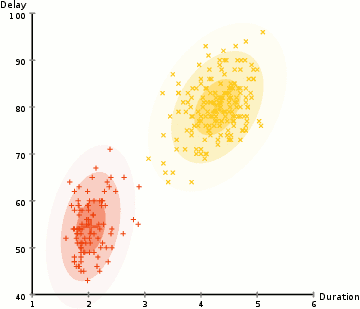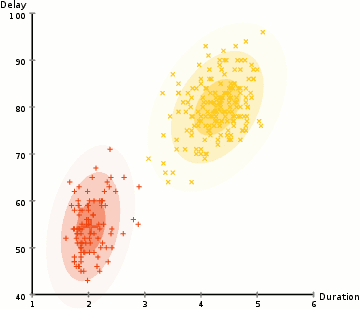
EM: the algorithm
Choose N “centers” guesses (like in K-means) repeat Expectation step: Calculate the probability of each distribution given the points Maximization step: Calculate the new centers and variances as weighted averages of the datapoints, weighted by the probabilities untill (convergence) e.g. when gaussian parameters no longer change
Expectatin Maximization:
Order: #clusters #dimensions #iterations #datapoints #parameters O(KdNp) (>K-means)
based on Bayes theorem
Its non-deterministic: the result depends on the (random) starting point (like K-mean)
It only works where a probability distribution for the data points can be defines (or equivalently a likelihood) (like K-mean)
Must declare the number of clusters and the shape of the pdf upfront (like K-mean)
Convergence Criteria
General
Any time you have an objective function (or loss function) you need to set up a tolerance : if your objective function did not change by more than ε since the last step you have reached convergence (i.e. you are satisfied)
ε is your tolerance
For clustering:
convergence can be reached if
no more than n data point changed cluster
n is your tolerance
6
Hierarchical clustering
Hierarchical clustering
removes the issue of
deciding K (number of
clusters)

Hierarchical clustering
it calculates distance between clusters and single points: linkage
6.1
Agglomerative
hierarchical clustering
Hierarchical clustering
agglomerative (bottom up)


dataset
Cluster Visualization "dendrogram"
Hierarchical clustering
agglomerative (bottom up)


Hierarchical clustering
agglomerative (bottom up)




Hierarchical clustering
agglomerative (bottom up)





Hierarchical clustering
agglomerative (bottom up)






distance
Agglomerative clustering
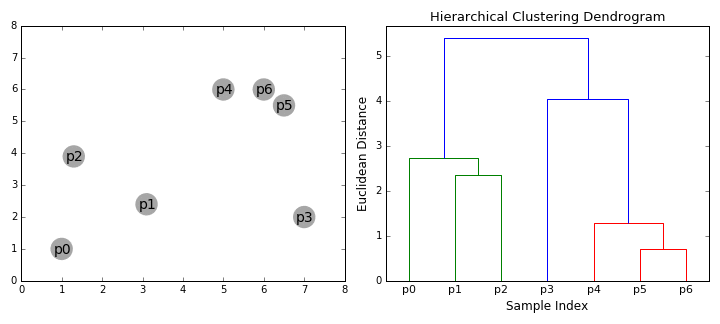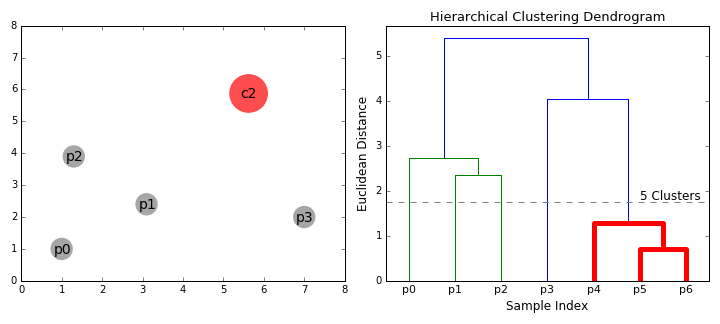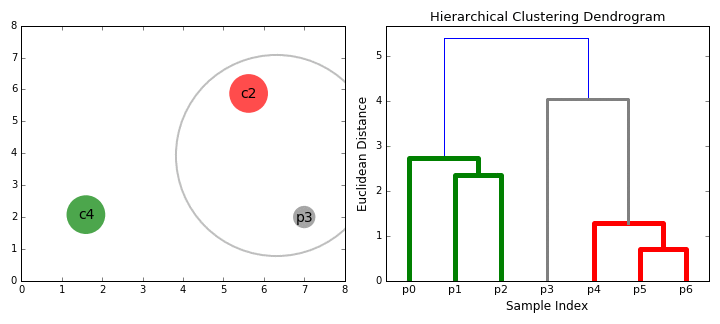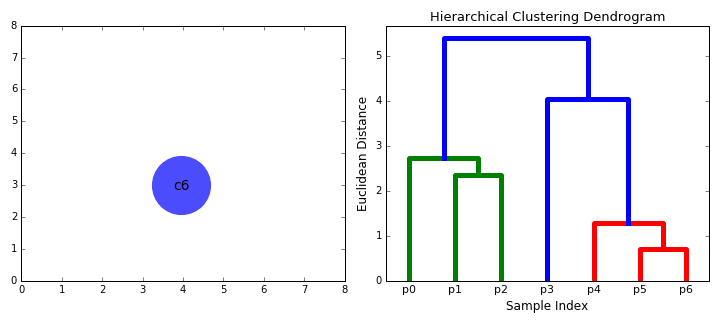
Hierarchical clustering
agglomerative (bottom up)
it's deterministic!
Hierarchical clustering
agglomerative (bottom up)

it's deterministic!
computationally intense because every cluster pair distance has to be calculate
Hierarchical clustering
agglomerative (bottom up)

it's deterministic!
computationally intense because every cluster pair distance has to be calculate
it is slow, though it can be optimize:
complexity
Agglomerative clustering:
the algorithm
compute the distance matrix
each data point is a singleton cluster
repeat
merge the 2 cluster with minimum distance
update the distance matrix
untill
only a single (n) cluster(s) remains
Order:
PROs
It's deterministic
CONs
It's greedy (optimization is done step by step and agglomeration decisions cannot be undone)
It's computationally expensive
Agglomerative clustering:
Agglomerative clustering: hyperparameters
- n_clusters : number of clusters (but you dont have to!)
- affinity : the distance/similarity definition
- linkage : the scheme to measure distance to a cluster
- random_state : for reproducibility

Agglomerative clustering: visualizing the dandrogram
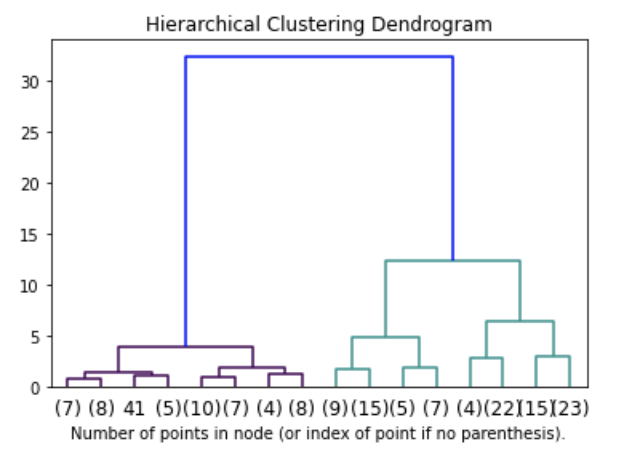
distance between a point and a cluster:
single link distance
D(c1,c2) = min(D(xc1, xc2))
linkage:
distance between a point and a cluster:

single link distance
D(c1,c2) = min(D(xc1, xc2))
complete link distance
D(c1,c2) = max(D(xc1, xc2))
linkage:
distance between a point and a cluster:

single link distance
D(c1,c2) = min(D(xc1, xc2))
complete link distance
D(c1,c2) = max(D(xc1, xc2))
centroid link distance
D(c1,c2) = mean(D(xc1, xc2))
linkage:
linkage:
distance between a point and a cluster:

single link distance
D(c1,c2) = min(D(xc1, xc2))
complete link distance
D(c1,c2) = max(D(xc1, xc2))
centroid link distance
D(c1,c2) = mean(D(xc1, xc2))
Ward distance (global measure)
6.2
Divisive hierarchical clustering
Hierarchical clustering
divisive (top down)

Hierarchical clustering
divisive (top down)



Hierarchical clustering
divisive (top down)







it is
non-deterministic
(like k-mean)
Hierarchical clustering
divisive (top down)







it is
non-deterministic
(like k-mean)
it is greedy -
just as k-means
two nearby points
may end up in
separate clusters
Hierarchical clustering
divisive (top down)







it is
non-deterministic
(like k-mean)
it is greedy -
just as k-means
two nearby points
may end up in
separate clusters
it is high complexity for
exhaustive search
But can be reduced (~k-means)
or
Divisive clustering:
the algorithm
Calculate clustering criterion for all subgroups, e.g. min intracluster variance
repeat split the best cluster based on criterion above untill each data is in its own singleton cluster
Order: (w K-means procedure)
It's non-deterministic: the result depends on the (random) starting point (like K-mean) unless its exaustive (but that is )
or
It's greedy (optimization is done step by step)
Divisive clustering:
7
Density Based
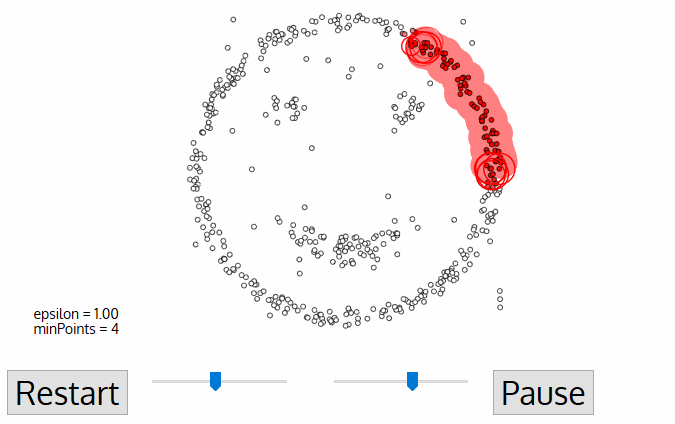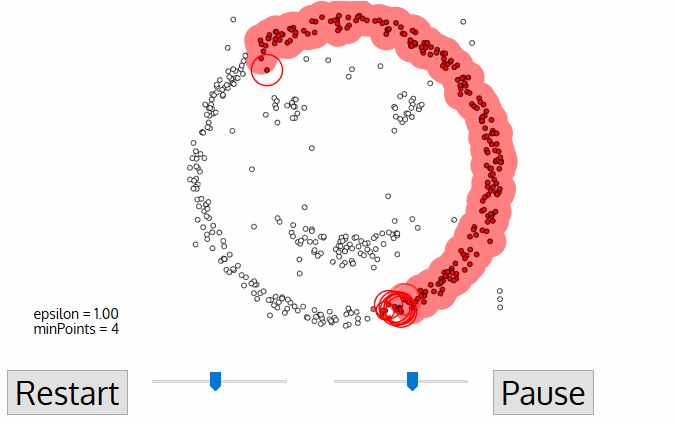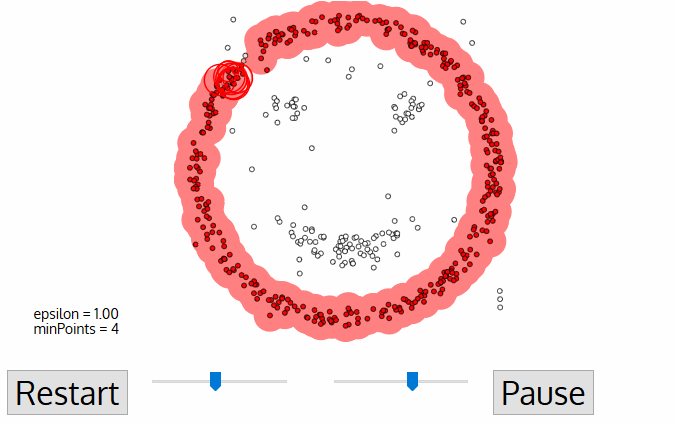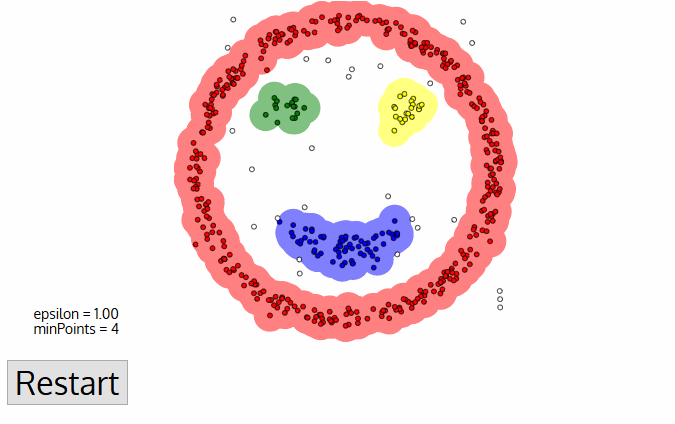
DBSCAN
DBSCAN
Density-based spatial clustering of applications with noise
DBSCAN is one of the most common clustering algorithms and also most cited in scientific literature
DBSCAN
defines cluster membership based on local density: based on Nearest Neighbors algorithm.
DBSCAN:
the algorithm
-
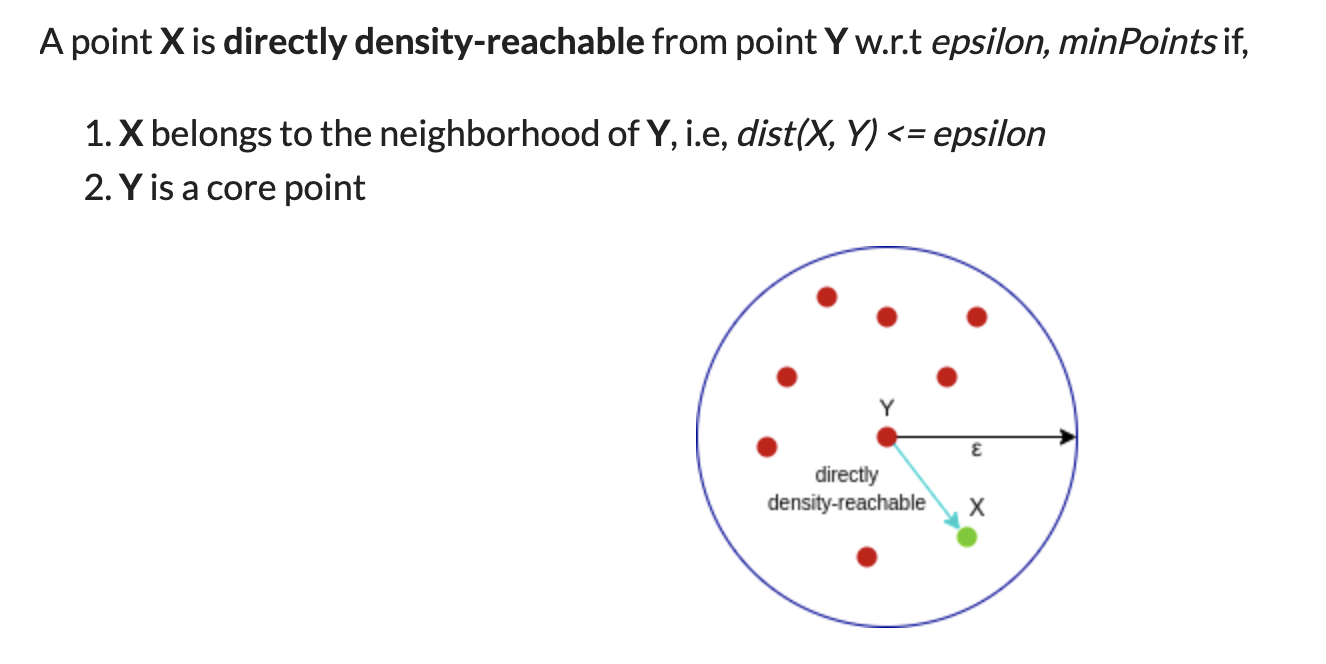
A point p is a core point if at least minPts points are within distance ε (including p).
-
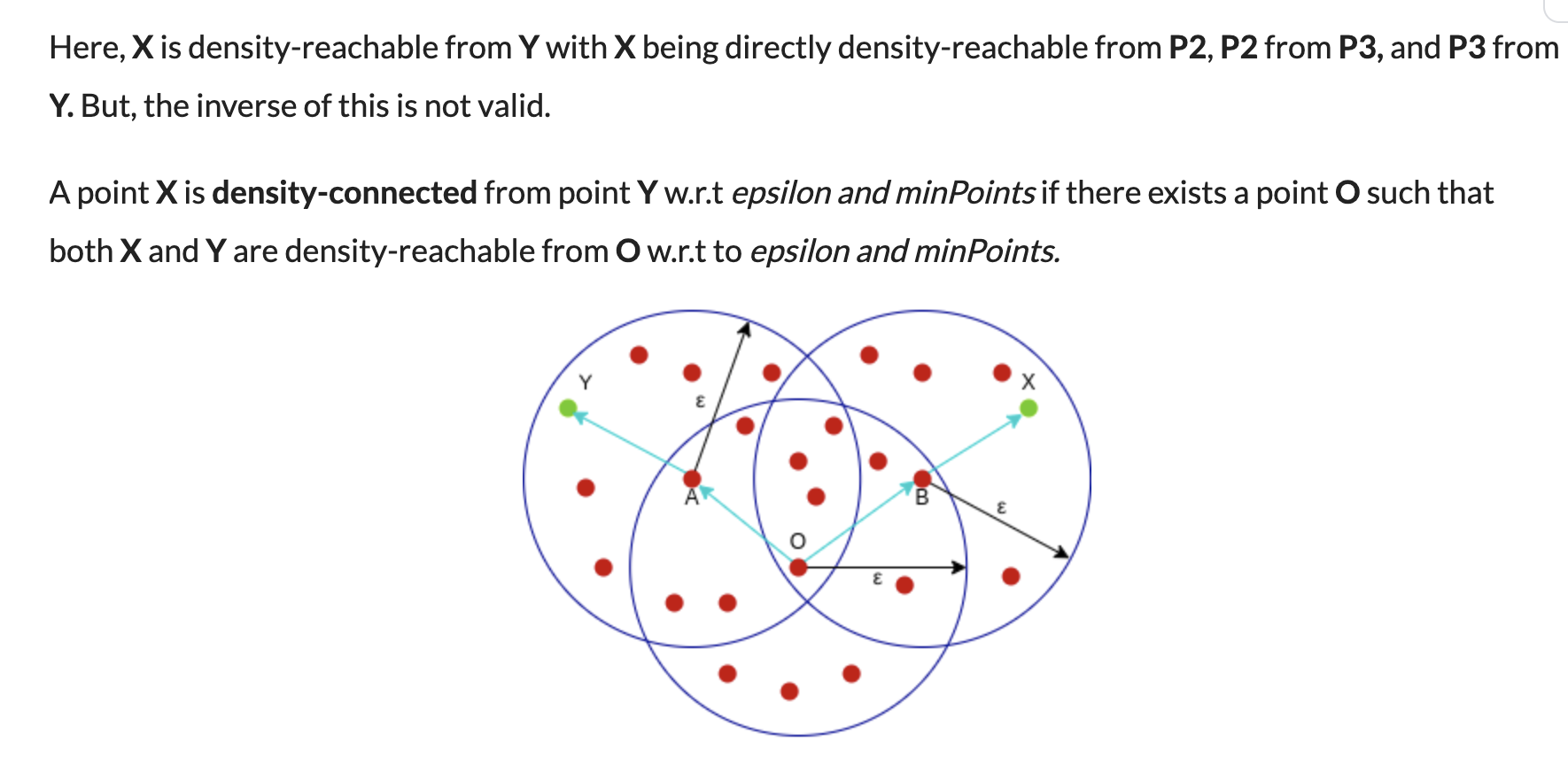
A point q is directly reachable from p if point q is within distance ε from core point p. Reachable from p if there is a path p1, ..., pn with p1 = p and pn = q, where each pi+1 is directly reachable from pi.
-
All points not reachable from any other point are outliers or noise points.
DBSCAN
Density-based spatial clustering of applications with noise
minPts
minimum number of points to form a dense region
maximum distance for points to be considered part of a cluster
ε
Key Hyperparameters:
Density-based spatial clustering of applications with noise
Key Hyperparameters:
minPts
minimum number of points to form a dense region
ε
maximum distance for points to be considered part of a cluster
2 points are considered neighbors if distance between them <= ε
DBSCAN
Density-based spatial clustering of applications with noise
minPts
ε
maximum distance for points to be considered part of a cluster
minimum number of points to form a dense region
2 points are considered neighbors if distance between them <= ε
regions with number of points >= minPts are considered dense
DBSCAN
Key Hyperparameters:
ε
minPts = 3
DBSCAN
slides: Farid Qmar
ε
minPts = 3
slides: Farid Qmar
DBSCAN
ε
minPts = 3
ε
slides: Farid Qmar
DBSCAN
ε
minPts = 3
directly reachable
slides: Farid Qmar
DBSCAN
ε
minPts = 3
core
dense region
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
directly reachable to
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
reachable to
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
reachable
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
ε
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
directly reachable
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
core
dense region
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
reachable
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
slides: Farid Qmar
DBSCAN
DBSCAN
ε
minPts = 3
noise/outliers
slides: Farid Qmar
DBSCAN
DBSCAN
DBSCAN
DBSCAN
PROs:
- Does not require knowledge of the number of clusters
- Deals with (and identifies) noise and outliers
- Capable of finding arbitrarily shaped and sized clusters
CONs:
- Highly sensitive to choice of ε and minPts
- cannot work for clusters with different densities
DBSCAN
DBSCAN:
the algorithm
-
ε : minimum distance to join points
-
min_sample : minimum number of points in a cluster, otherwise they are labeled outliers.
-
metric : the distance metric
-
p : float, optional The power of the Minkowski metric

DBSCAN:
the algorithm
-
ε : minimum distance to join points
-
min_sample : minimum number of points in a cluster, otherwise they are labeled outliers.
-
metric : the distance metric
-
p : float, optional The power of the Minkowski metric

its extremely sensitive to these parameters!
DBSCAN:
the algorithm
for each point P count neighbours within minPts: label=C for each point P ~= C measure distance d to all Cs if d<minD: label = DR for each point P not C and not DR if distance d to C or DR > minD: label = outlier if distance d to C or DR <= minD: find path to closet C and cluster
Order:
PROs
Deterministic.
Deals with noise and outliers
Can be used with any definition of distance or similarity
PROs
Not entirely deterministic.
Only works in a constant density field
DBSCAN clustering:
a really good blog post on DBScan
https://www.analyticsvidhya.com/blog/2020/09/how-dbscan-clustering-works/
DBSCAN clustering:

key concepts
Clustering : unsupervised learning where all features are observed for all datapoints. The goal is to partition the space into maximally homogeneous maximally distinguished groups
clustering is easy, but interpreting results is tricky
Distance : A definition of distance is required to group observations/ partition the space.
Common distances over continuous variables
- Minkowski (inlcudes Euclidian = Minkowski(2)
- Great Circle (for coordinated on a sphere, e.g. earth or sky)
Common distances over categorical variables:
- Simple Distance Matrix
- Jaccard Distance
Whitening
Models assume that the data is not correlated. If your data is correlated the model results may be invalid. And your data always has correlations.
- whiten the data by using the matrix that diagonalizes the covariance matrix. This is ideal but computationally expensive if possible at all
- scale your data so that each feature is mean=0 stdev=2.
Solution:
key concepts
Partition clustering:
Hard: K-means O(KdN) , needs to decide the number of clusters, non deterministic
simple efficient implementation but the need to select the number of clusters is a significant flaw
Soft: Expectation Maximization O(KdNp) , needs to decide the number of clusters, need to decide a likelihood function (parametric), non deterministic
Hierarchical:
Divisive: Exhaustive ; at least non deterministic
Agglomerative: , deterministic, greedy. Can be run through and explore the best stopping point. Does not require to choose the number of clusters a priori
Density based
DBSCAN: Density based clustering method that can identify outliers, which means it can be used in the presence of noise. Complexity . Most common (cited) clustering method in the natural sciences.
key concepts
encoding categorical variables:
variables have to be encoded as numbers for computers to understand them. You can encode categorical variables with integers or floating point but you implicitly impart an order. The standard is to one-hot-encode which means creating a binary (True/False) feature (column) for each category of a categorical variables but this increases the feature space and generated covariance.
model diagnostics for classifiers: Fraction of True Positives and False Positives are the metrics to evaluate classifiers. Combinations of those numbers include Accuracy (TP/ (TP+FP)), Precision (TP/(TP+FN)), Recall ((TP+TN)/(TP+TN+FP+FN)).
ROC curve: (TP vs FP) is a holistic metric of a model. It can be used to guide the choice of hyperparameters to find the "sweet spot" for your problem
resources
a comprehensive review of clustering methods
Data Clustering: A Review, Jain, Mutry, Flynn 1999
https://www.cs.rutgers.edu/~mlittman/courses/lightai03/jain99data.pdf
a blog post on how to generate and interpret a scipy dendrogram by Jörn Hees
https://joernhees.de/blog/2015/08/26/scipy-hierarchical-clustering-and-dendrogram-tutorial/
reading
Any of these papers: