foundations of data science for everyone

V: Stochastic Gradient Descent &
   Multiple Linear Regression

AUTHOR AND LECTURER: Farid Qamar

this slide deck: https://slides.com/faridqamar/fdfse_5

1

optimizing the objective function

what is a model?

in the ML context:

a model is a low dimensional representation of a higher dimensionality dataset

recall:

what is a machine learning?

ML: Any model with parameters learned from the data

what is a machine learning?

ML: Any model with parameters learned from the data

ML models are a parameterized representation of "reality" where the parameters are learned from finite sets (samples) of realizations of that reality (population)

how do we model?

Choose the model:

a mathematical formula to represent the behavior in the data

1

example: line model y = a x + b

parameters

how do we model?

Choose the model:

a mathematical formula to represent the behavior in the data

1

example: line model y = a x + b

parameters

Choose the hyperparameters:

parameters chosen before the learning process, which govern the model and training process

example: the degree N of the polynomial

y = \sum^N_{i=0}c_i x^i

how do we model?

Choose an objective function:

in order to find the "best" parameters of the model: we need to "optimize" a function.

We need something to be either MINIMIZED or MAXIMIZED

2

example:

line model: y = a x + b

parameters

objective function: sum of residual squared (least square fit method)

SSE = \sum(y_{i,observed}-y_{i,predicted})^2
SSE = \sum(y_{i,observed}-(ax_i+b))^2

we want to minimize SSE as much as possible

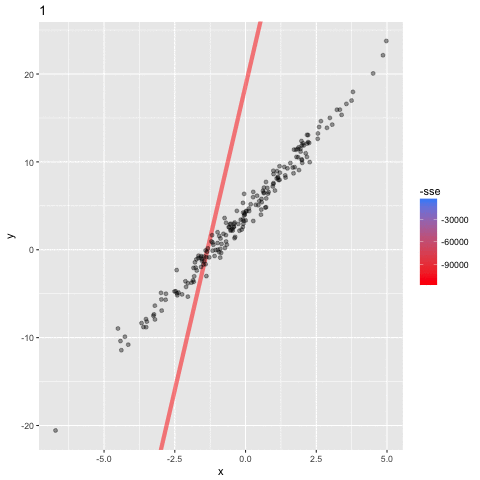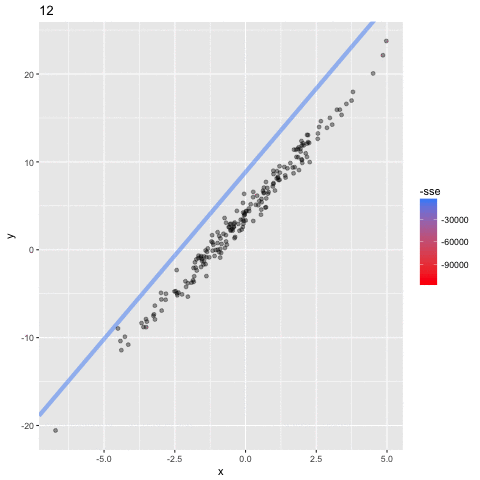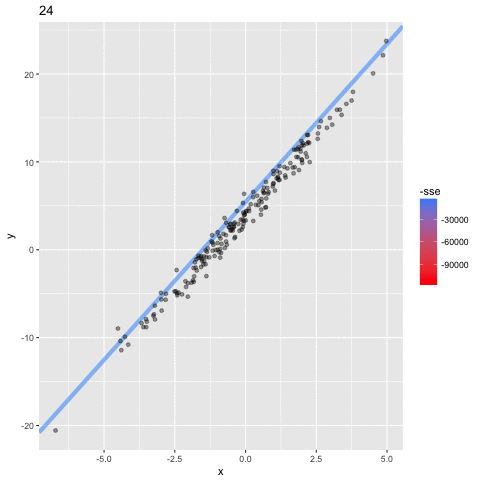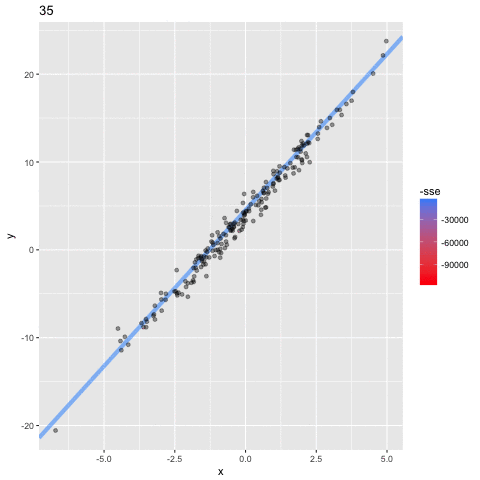
Optimizing the Objective Function

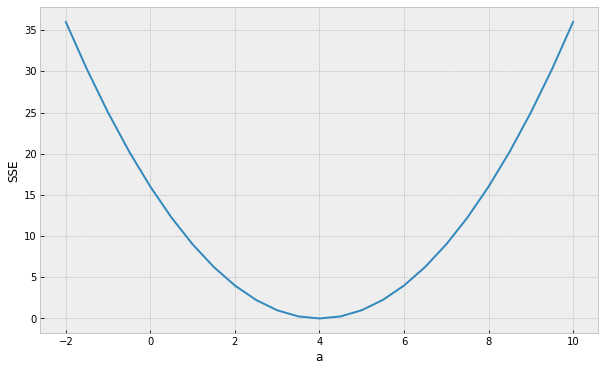
assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

Minimum (optimal) SSE

     a = 4

Optimizing the Objective Function

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

How do we find the minimum if we do not know beforehand how the SSE curve looks like?

Optimizing the Objective Function

Minimum (optimal) SSE

     a = 4

1

.

1

stochastic gradient descent (SGD)

the algorithm: Stochastic Gradient Descent (SGD)

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

-1

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

2. calculate the SSE

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

4. step in that direction

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

4. step in that direction

5. go back to step 2 and repeat

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

4. step in that direction

5. go back to step 2 and repeat

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

4. step in that direction

5. go back to step 2 and repeat

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

4. step in that direction

5. go back to step 2 and repeat

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

4. step in that direction

5. go back to step 2 and repeat

the algorithm: Stochastic Gradient Descent

assume a simpler line model   y = ax 

(b = 0) so we only need to find the "best" parameter a

1. choose initial value for a

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

4. step in that direction

5. go back to step 2 and repeat

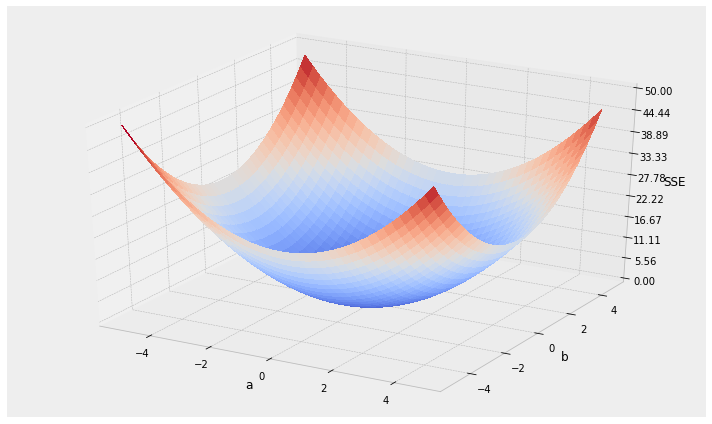
the algorithm: Stochastic Gradient Descent

for a line model   y = ax + b 

we need to find the "best" parameters a and b

1. choose initial value for a & b

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

4. step in that direction

5. go back to step 2 and repeat

the algorithm: Stochastic Gradient Descent

for a line model   y = ax + b 

we need to find the "best" parameters a and b

1. choose initial value for a & b

2. calculate the SSE

3. calculate best direction to              go to decrease the SSE

4. step in that direction

5. go back to step 2 and repeat

the algorithm: Stochastic Gradient Descent

Things to consider:

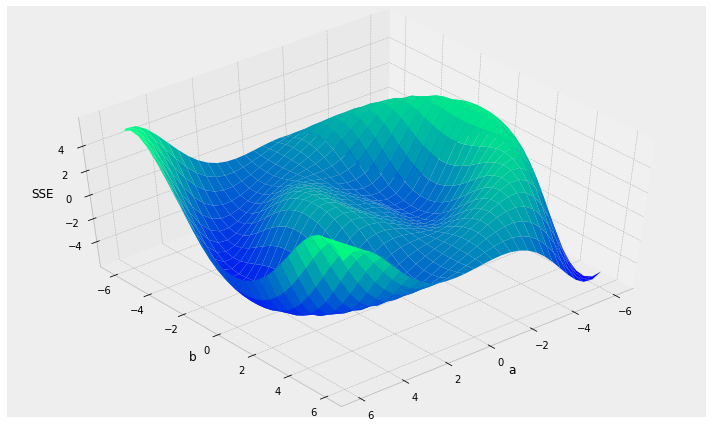
the algorithm: Stochastic Gradient Descent

Things to consider:

-  local vs. global minima

 

local minima

global minimum

the algorithm: Stochastic Gradient Descent

Things to consider:

-  local vs. global minima

-  initialization: choosing starting spot?

global minimum

local minima

the algorithm: Stochastic Gradient Descent

Things to consider:

-  local vs. global minima

-  initialization: choosing starting spot?

-  learning rate: how far to step?

the algorithm: Stochastic Gradient Descent

Things to consider:

-  local vs. global minima

-  initialization: choosing starting spot?

-  learning rate: how far to step?

-  stopping criterion: when to stop?

the algorithm: Stochastic Gradient Descent

Things to consider:

-  local vs. global minima

-  initialization: choosing starting spot?

-  learning rate: how far to step?

-  stopping criterion: when to stop?

Stochastic Gradient Descent (SGD): use a different (random) sub-sample of the data at each iteration

2

multiple linear regression

ML terminology

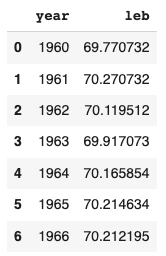
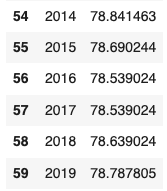
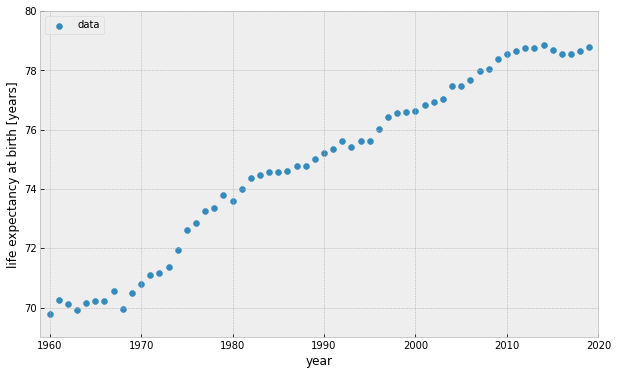
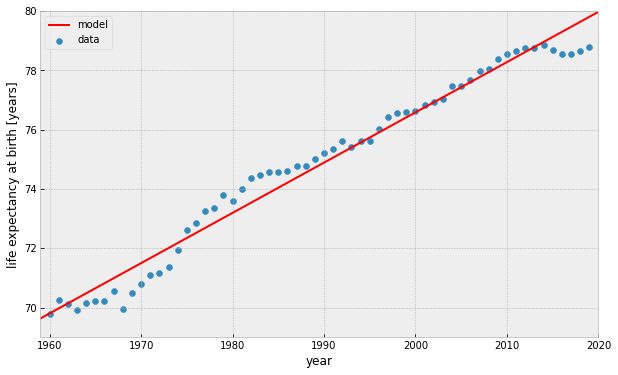
World Bank: Life expectancy at birth in the US

ML terminology

World Bank: Life expectancy at birth in the US

ML terminology

World Bank: Life expectancy at birth in the US

model

ML terminology

World Bank: Life expectancy at birth in the US

object

model

ML terminology

World Bank: Life expectancy at birth in the US

object

feature

model

ML terminology

World Bank: Life expectancy at birth in the US

object

feature

target

model

ML terminology

objects

features

target

ML terminology

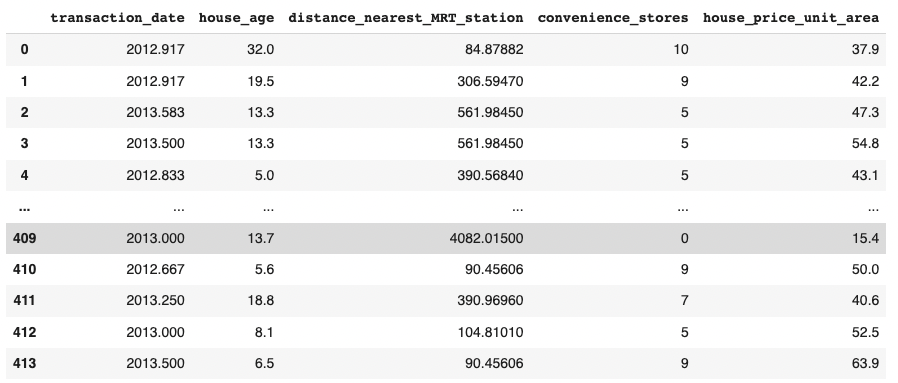
features

target

objects

Simple Linear Regression

1  feature

1  target

2  parameters

y = ax + b

Simple Linear Regression

1  feature

1  target

2  parameters

y = ax + b
y = \beta_0 + \beta_1x_1

Simple Linear Regression

1  feature

1  target

2  parameters

y = ax + b
y = \beta_0 + \beta_1x_1

Multiple Linear Regression

n  features

1  target

Simple Linear Regression

1  feature

1  target

2  parameters

y = ax + b
y = \beta_0 + \beta_1x_1

Multiple Linear Regression

y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_3 + ... + \beta_nx_n

n  features

1  target

n+1 parameters

Simple Linear Regression

1  feature

1  target

2  parameters

y = ax + b
y = \beta_0 + \beta_1x_1

Multiple Linear Regression

y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_3 + ... + \beta_nx_n
y = \sum_{i=0}^n \beta_ix_i
x_0 = \vec{1}

;

n  features

1  target

n+1 parameters