foundations of data science for everyone
IX: Clustering
Farid Qamar
this slide deck: https://slides.com/federicabianco/fdsfe_8
1
clustering
Machine Learning
unsupervised learning
identify features and create models that allow to understand structure in the data
unsupervised learning
identify features and create models that allow to understand structure in the data
supervised learning
extract features and create models that allow prediction where the correct answer is known for a subset of the data
unsupervised learning
identify features and create models that allow to understand structure in the data
unsupervised learning
identify features and create models that allow to understand structure in the data
supervised learning
extract features and create models that allow prediction where the correct answer is known for a subset of the data
- clustering
- Principle Component Analysis
- Apriori (association rule)
- k-Nearest Neighbors
- regression
- Support Vector Machines
- Classification/Regression Trees
- Neural Networks
Machine Learning
objects
features
target
Supervised ML
data as a function of another number characterizing the system
Unsupervised ML
objects
features
data is represented by objects, each of which has associated features
Unsupervised ML
example data object:

Flatiron Building, NYC
wikipedia.org/wiki/Flatiron_Building
example features:
- height
- energy use
- number of floors
- number of occupants
- age in years
- zipcode
- footprint
- owner
float
float
integer
integer
integer
integer/string
array (lat/lon)
string
Unsupervised ML
Nf = number of features
No = number of objects
2D dataset (Nf x No)

https://www.netimpact.org/chapters/new-york-city-professional
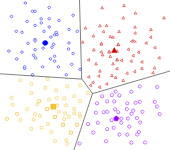
Clustering
Goal:
Find a pattern by dividing the objects into groups such that the objects within a group are more similar to each other than objects outside the group
Clustering
Goal:
Find a pattern by dividing the objects into groups such that the objects within a group are more similar to each other than objects outside the group
Internal Criterion:
members of the cluster should be similar to each other (intra-cluster compactness)
External Criterion:
objects outside the cluster should be dissimilar from the objects inside the cluster
Internal Criterion:
members of the cluster should be similar to each other (intra-cluster compactness)
External Criterion:
objects outside the cluster should be dissimilar from the objects inside the cluster










Internal Criterion:
members of the cluster should be similar to each other (intra-cluster compactness)
External Criterion:
objects outside the cluster should be dissimilar from the objects inside the cluster









mammals
birds
fish
zoologist's clusters

Internal Criterion:
members of the cluster should be similar to each other (intra-cluster compactness)
External Criterion:
objects outside the cluster should be dissimilar from the objects inside the cluster









walk
fly
swim
mobility clusters

Internal Criterion:
members of the cluster should be similar to each other (intra-cluster compactness)
External Criterion:
objects outside the cluster should be dissimilar from the objects inside the cluster









orange/red/green
black/white/blue
photographer's clusters

Internal Criterion:
members of the cluster should be similar to each other (intra-cluster compactness)
External Criterion:
objects outside the cluster should be dissimilar from the objects inside the cluster
The optimal clustering depends on
- how you define similarity/distance
- the purpose of the clustering
Clustering
Find a pattern by dividing the objects into groups such that the objects within a group are more similar to each other than objects outside the group
Goal:
- Define similarity/dissimilarity function
- Figure out the grouping of objects based on the chosen similarity/dissimilarity function
- Objects within a cluster are similar
- Objects across clusters are not so similar
How:
distance metrics
continuous variables
Minkowski family of distances
Euclidean: p=2
features: x, y
distance metrics
continuous variables
Minkowski family of distances

Manhattan: p=1
features: x, y
distance metrics
continuous variables
Minkowski family of distances

Manhattan: p=1
features: x, y
distance metrics
continuous variables
Minkowski family of distances
L1 is the Minkowski distance with p=1
L2 is the Minkowski distance with p=2
Residuals
2
2
3
L1 = 7
L2 = 17
distance metrics
Minkowski family of distances
Great Circle distance
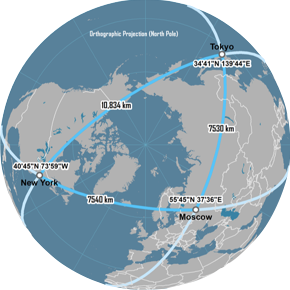
features
latitude and longitude
continuous variables
distance metrics
Simple Matching Distance
Uses presence/absence of features in data
: number of features in neither
: number of features in both
: number of features in i but not j
: number of features in j but not i
Simple Matching Coefficient
or Rand similarity
| 1 | 0 | sum | |
|---|---|---|---|
| 1 | M11 | M10 | M11+M10 |
| 0 | M01 | M00 | M01+M00 |
| sum | M11+M01 | M10+M00 | M11+M00+M01+ M10 |
observation i
observation j
}
}
categorical variables:
binary
3
whitening
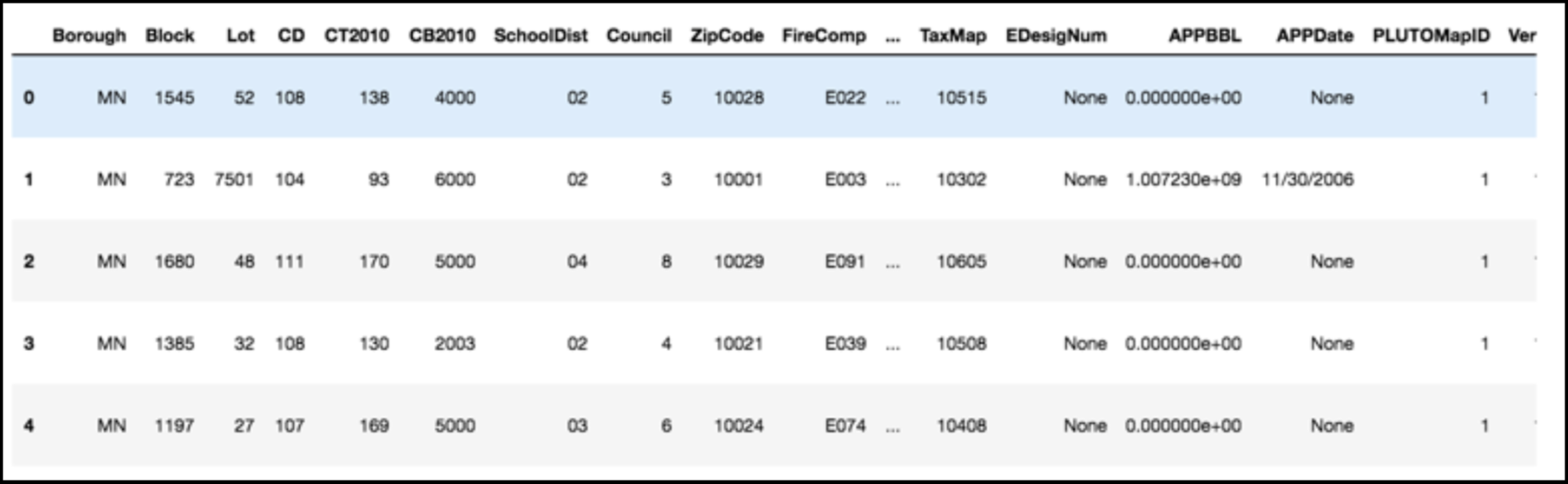
Data can have covariance (and it almost always does!)
PLUTO Manhattan data (42,000 x 15)
axis 1 -> features
axis 0 -> observations
Data can have covariance (and it almost always does!)
Data can have covariance (and it almost always does!)
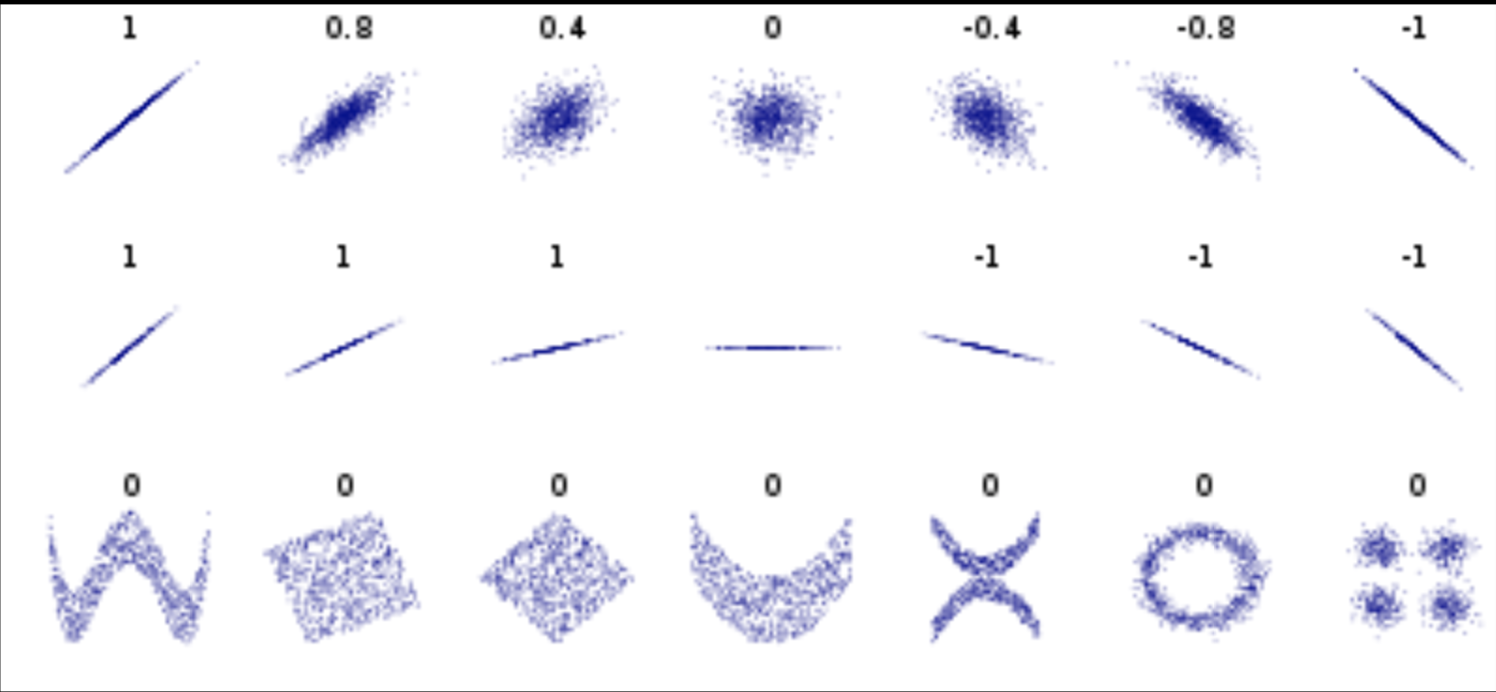
Pearson's correlation (linear correlation)
correlation = correlation / variance
PLUTO Manhattan data (42,000 x 15) correlation matrix
axis 1 -> features
axis 0 -> observations
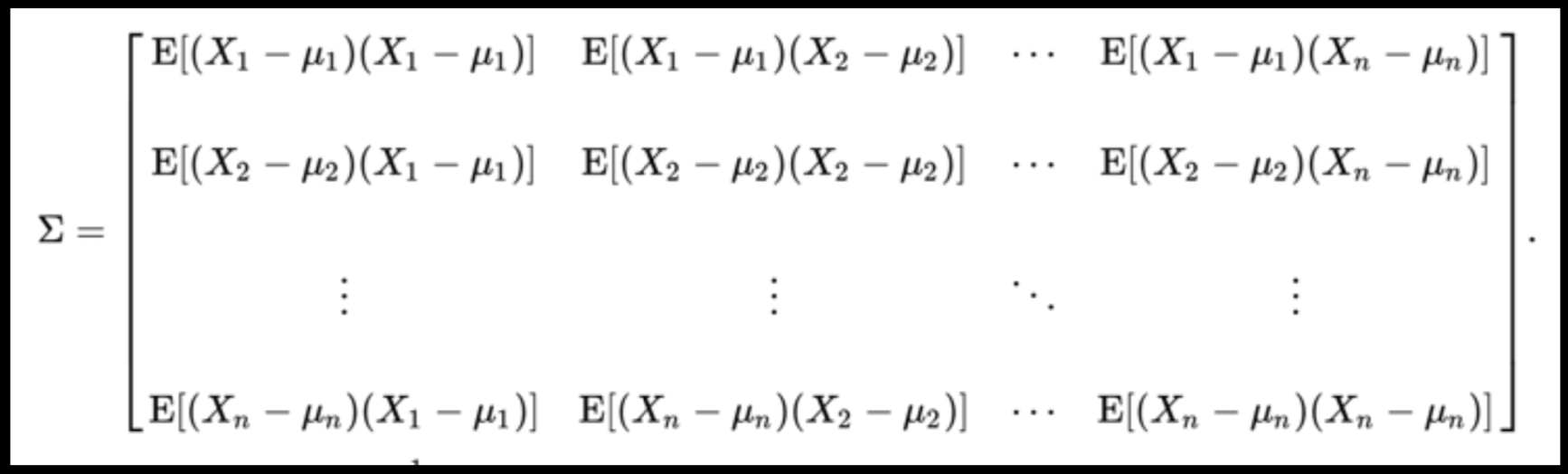
Data can have covariance (and it almost always does!)
PLUTO Manhattan data (42,000 x 15) correlation matrix
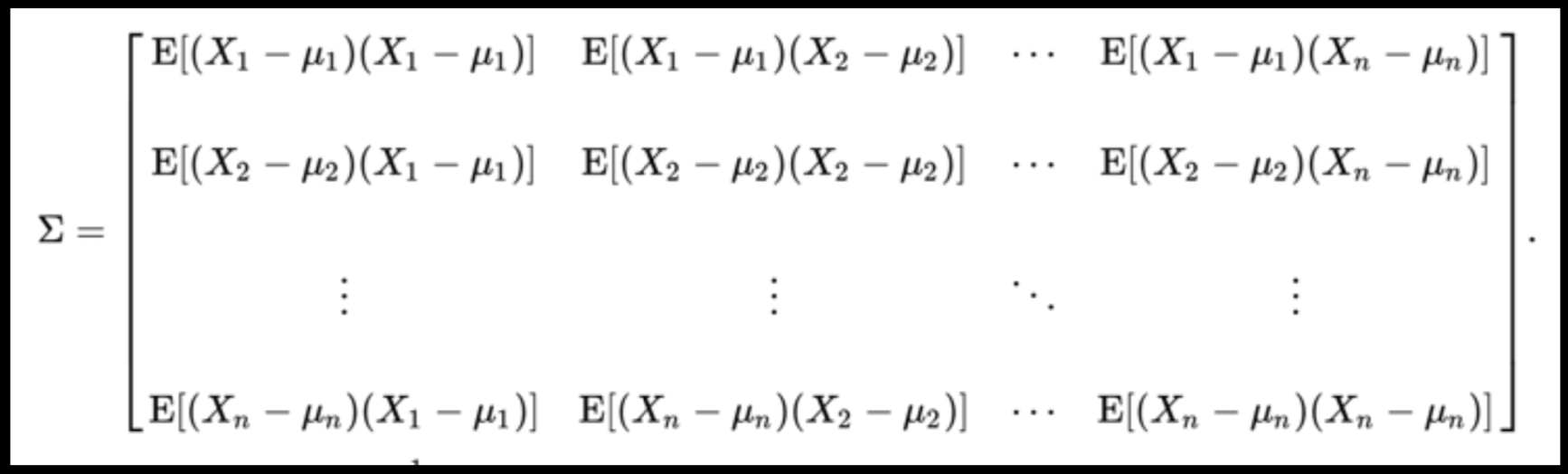

A covariance matrix is diagonal if the data has no correlation
Data can have covariance (and it almost always does!)
Generic preprocessing... WHY??
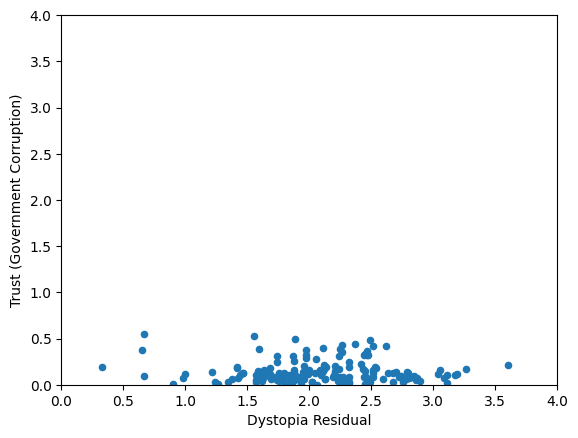
Worldbank Happyness Dataset https://github.com/fedhere/MLPNS_FBianco/blob/main/clustering/happiness_solution.ipynb
Skewed data distribution:
std(x) ~ range(y)
Clustering without scaling:
only the variable with more spread matters
Clustering without scaling:
both variables matter equally
Generic preprocessing... WHY??


Worldbank Happyness Dataset https://github.com/fedhere/MLPNS_FBianco/blob/main/clustering/happiness_solution.ipynb
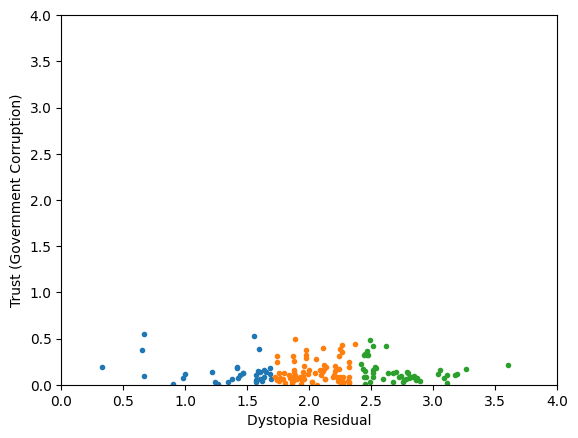
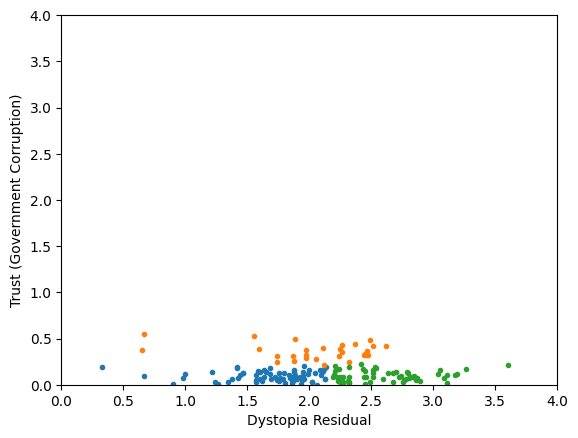
Skewed data distribution:
std(x) ~ 2*range(y)
Clustering without scaling:
only the variable with more spread matters
Clustering without scaling:
both variables matter equally
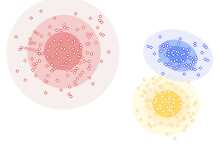
Data that is not correlated appear as a sphere in the Ndimensional feature space
Data can have covariance (and it almost always does!)
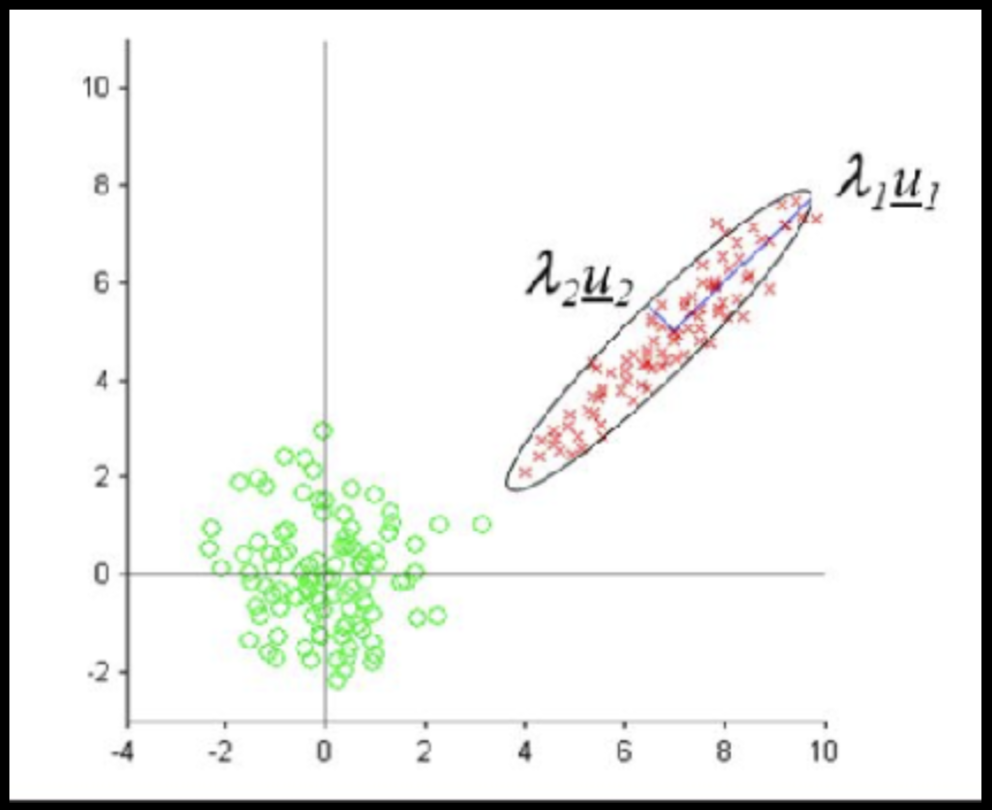
ORIGINAL DATA
STANDARDIZED DATA
Generic preprocessing
Generic preprocessing
for each feature: divide by standard deviation and subtract mean
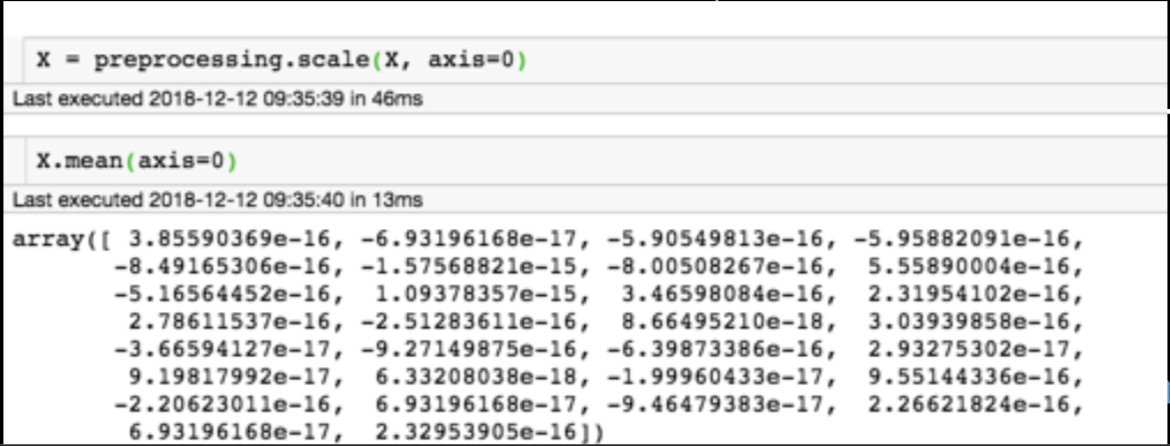

mean of each feature should be 0, standard deviation of each feature should be 1

Generic preprocessing: most commonly, we will just correct for the spread and centroid
2
k-Means clustering
Clustering
we can define similarity in terms of distance
common measure of distance is the squared Euclidean distance
(aka., L2-norm, sum of squared differences)
also called the inertia
Clustering
example:
if the data is on buildings with the features: year built (Y) and energy use (E), the distance between two objects (1 and 2):
Types of Clustering
Density-based Clustering
Distribution-based Clustering
Hierarchical Clustering
Centroid-based Clustering
k-Means: the objective function
objective: minimizing the aggregate distance within the cluster
total intra-cluster variance =
hyperparameters: must declare the number of clusters prior to clustering
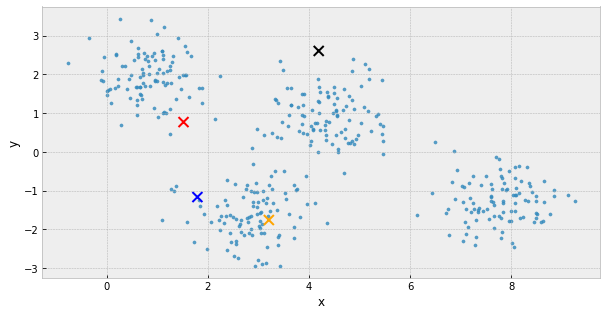
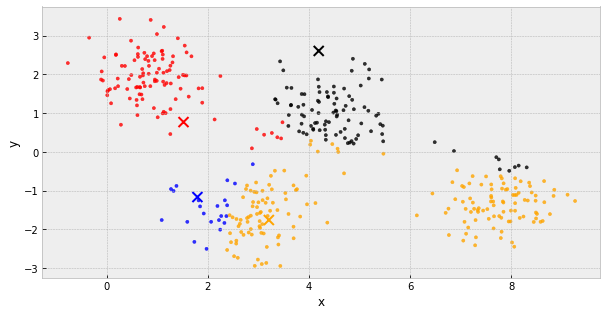
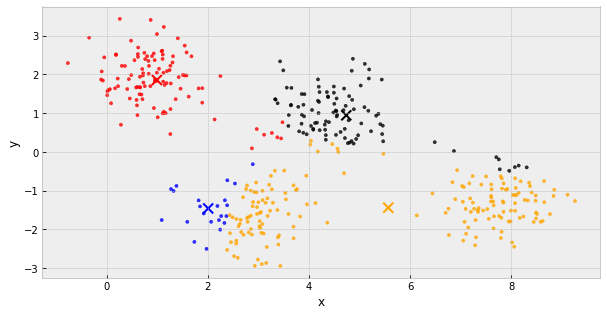
k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3
k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3
k-Means Clustering

- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3
k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3
k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3
k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3

k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3

k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
IF the inertia has not changed, stop
Else, go back to step 3

k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3
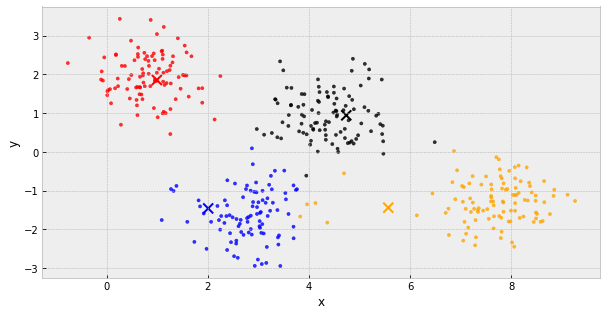
k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3
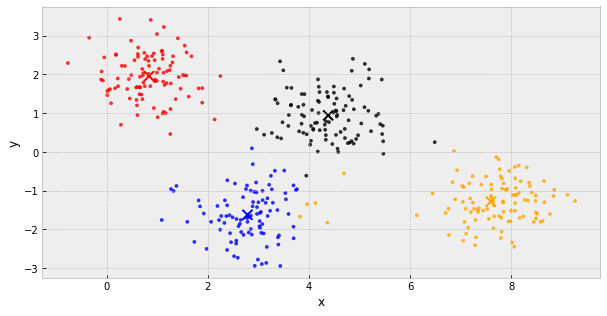
k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3

k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3

k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
IF the inertia has not changed, stop
Else, go back to step 3

k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3
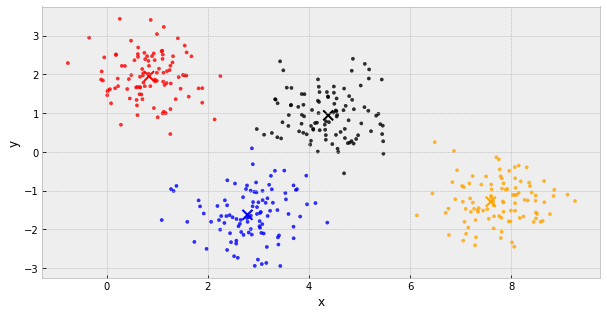
k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3
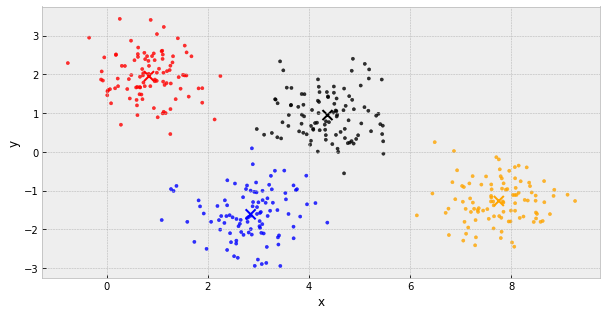
k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3

k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3

k-Means Clustering
- choose k initial centers
- calculate the inertia
- assign each object to the nearest cluster center
- update the cluster centers to be the average of their assigned population
- calculate the inertia
- IF the inertia has not changed, stop
Else, go back to step 3

choosing k clusters
2
.
1
if low number of variables:
Visualize and pick k manually
Choosing number of clusters k


or...use the Elbow Method
- Calculate the distance of all points to their nearest cluster center
- Calculate the inertia (sum the distances)
- Find the "Elbow"
- point after which the inertia starts decreasing linearly
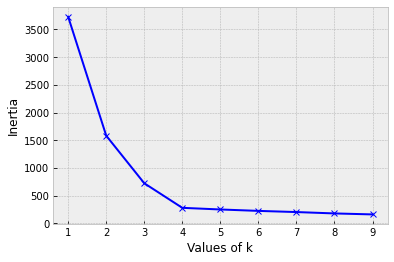
Choosing number of clusters k
or...use the Elbow Method
"Elbow" inflection point
Optimal k = 4 centers

- Calculate the distance of all points to their nearest cluster center
- Calculate the inertia (sum the distances)
- Find the "Elbow"
- point after which the inertia starts decreasing linearly
Choosing number of clusters k
or...use the Elbow Method
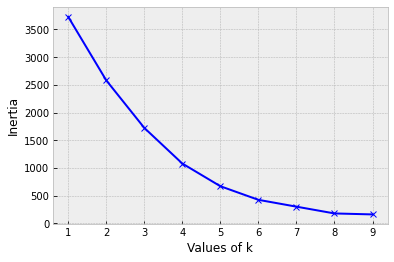
But...this doesn't always work!
- Calculate the distance of all points to their nearest cluster center
- Calculate the inertia (sum the distances)
- Find the "Elbow"
- point after which the inertia starts decreasing linearly
Choosing number of clusters k
problems with k-Means
2
.
2
Problems with k-Means
highly dependent on initial location of k centers

Problems with k-Means
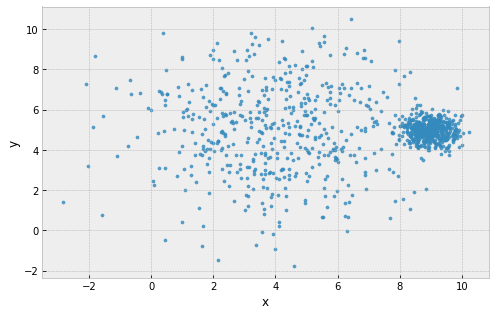
example: 2 clusters, one large and one small
clusters are assumed to all be the same size
Problems with k-Means
clusters are assumed to all be the same size

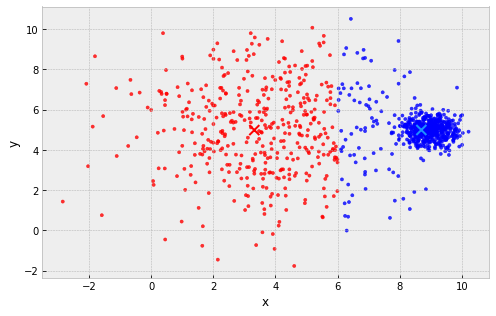
example: 2 clusters, one large and one small
Problems with k-Means
clusters are assumed to have the same extent in every direction
example: 2 'squashed' clusters with different widths in different directions
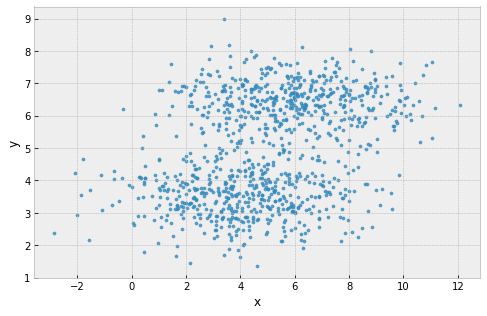
Problems with k-Means
example: 2 'squashed' clusters with different widths in different directions

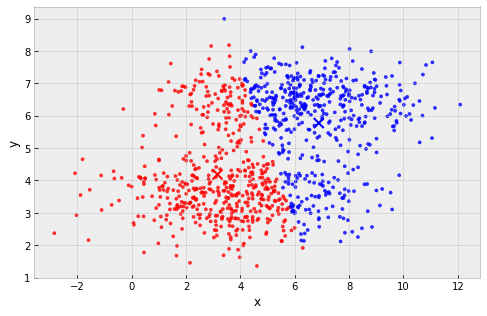
clusters are assumed to have the same extent in every direction
Problems with k-Means
clusters are must be linearly separable (convex sets)
example: 2 non-convex sets
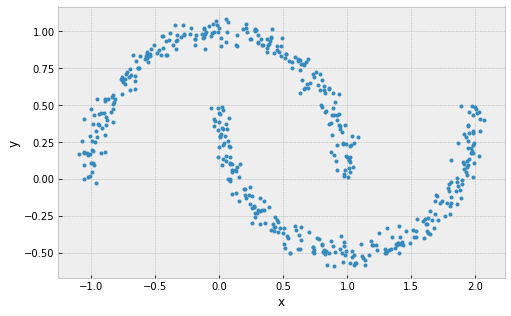
Problems with k-Means
example: 2 non-convex sets

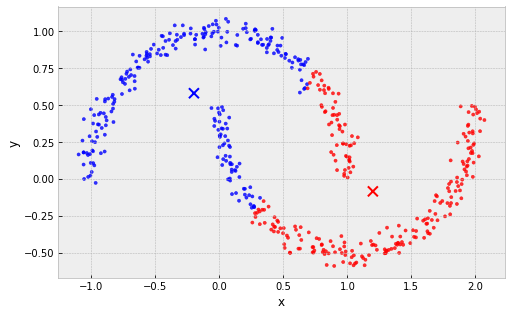
clusters are must be linearly separable (convex sets)
3
DBSCAN
DBSCAN
Density-based spatial clustering of applications with noise
One of the most common clustering algorithms and most cited in scientific literature
DBSCAN
Density-based spatial clustering of applications with noise
One of the most common clustering algorithms and most cited in scientific literature
Defines cluster membership based on local density:
Nearest Neighbors algorithm
DBSCAN
Density-based spatial clustering of applications with noise
Requires 2 parameters:
minPts
minimum number of points to form a dense region
maximum distance for points to be considered part of a cluster
ε
DBSCAN
Density-based spatial clustering of applications with noise
Requires 2 parameters:
minPts
minimum number of points to form a dense region
ε
maximum distance for points to be considered part of a cluster
2 points are considered neighbors if distance between them <= ε
DBSCAN
Density-based spatial clustering of applications with noise
Requires 2 parameters:
minPts
ε
maximum distance for points to be considered part of a cluster
minimum number of points to form a dense region
2 points are considered neighbors if distance between them <= ε
regions with number of points >= minPts are considered dense
DBSCAN
- A point p is a core point if at least minPts are within distance ε (including p)
- A point q is directly reachable from p if point q is within distance ε from core point p
- A point q is reachable from p if there is a path p1, ..., pn with p1 = p and pn = q, where each pi+1is directly reachable from pi
- All points not reachable from any other point are outliers or noise points
Algorithm:
DBSCAN
ε
minPts = 3
DBSCAN
ε
minPts = 3
DBSCAN
ε
minPts = 3
ε
DBSCAN
ε
minPts = 3
directly reachable
DBSCAN
ε
minPts = 3
core
dense region
DBSCAN
ε
minPts = 3
DBSCAN
ε
minPts = 3
directly reachable to
DBSCAN
ε
minPts = 3
reachable to
DBSCAN
ε
minPts = 3
DBSCAN
ε
minPts = 3
reachable
DBSCAN
ε
minPts = 3
DBSCAN
ε
minPts = 3
DBSCAN
ε
minPts = 3
ε
DBSCAN
ε
minPts = 3
directly reachable
DBSCAN
ε
minPts = 3
core
dense region
DBSCAN
ε
minPts = 3
reachable
DBSCAN
ε
minPts = 3
DBSCAN
ε
minPts = 3
noise/outliers
DBSCAN
DBSCAN
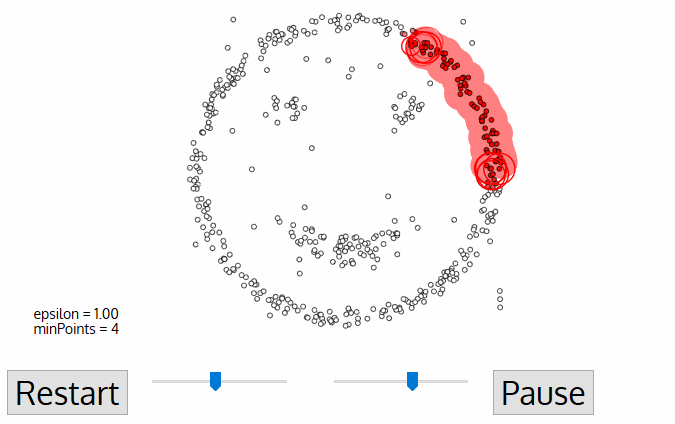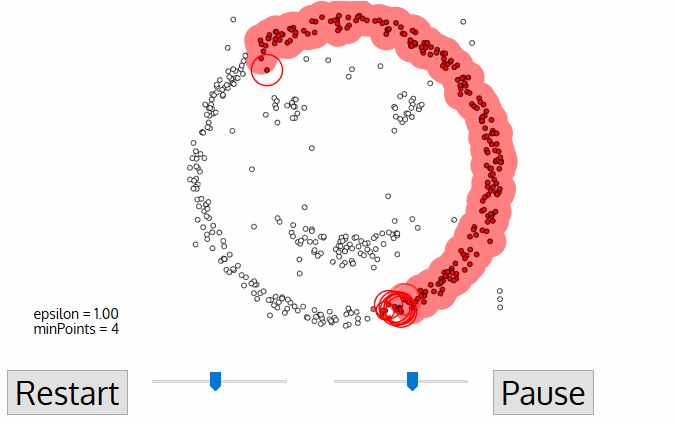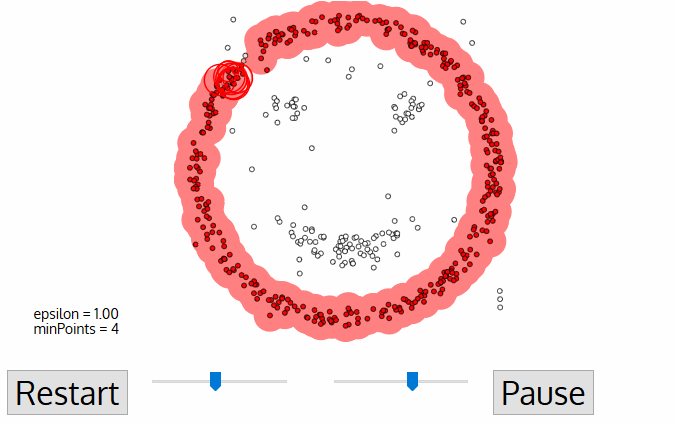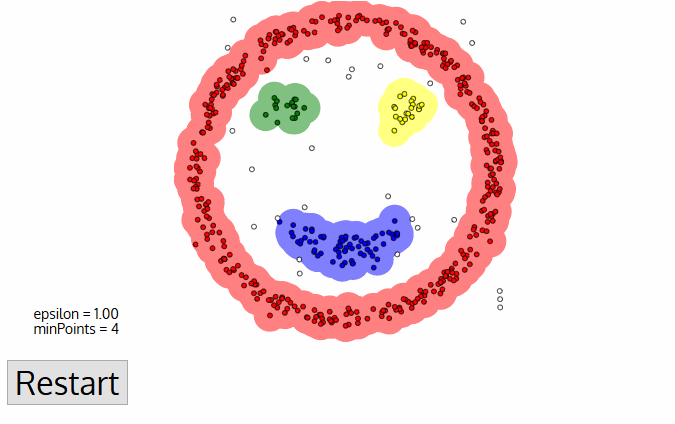
PROs:
- Does not require knowledge of the number of clusters
- Deals (and identifies) noise and outliers
- Capable of finding arbitrarily shaped and sized clusters
CONs:
- Highly sensitive to choice of ε and minPts
- cannot work for clusters with different densities
6
Hierarchical clustering
Hierarchical clustering
removes the issue of
deciding K (number of
clusters)

Hierarchical clustering
it calculates distance between clusters and single points: linkage
6.2
Agglomerative
hierarchical clustering
Hierarchical clustering
agglomerative (bottom up)


Hierarchical clustering
agglomerative (bottom up)




Hierarchical clustering
agglomerative (bottom up)





Hierarchical clustering
agglomerative (bottom up)






distance
Hierarchical clustering
agglomerative (bottom up)
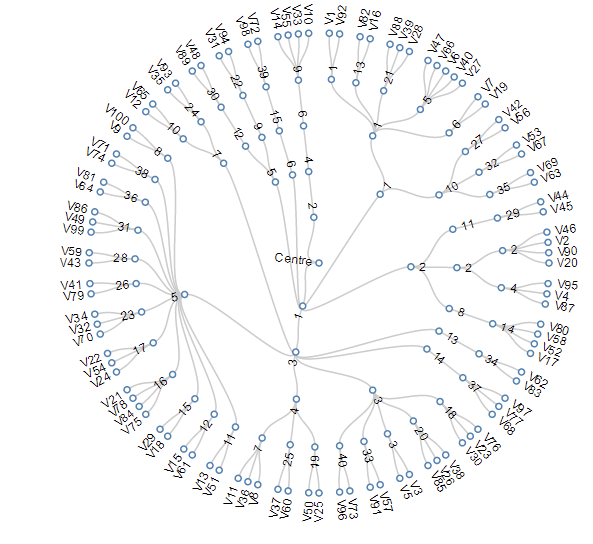
it's deterministic!
computationally intense because every cluster pair distance has to be calculate
it is slow, though it can be optimize:
complexity
Agglomerative clustering:
the algorithm
compute the distance matrix
each data point is a singleton cluster
repeat
merge the 2 cluster with minimum distance
update the distance matrix
untill
only a single (n) cluster(s) remains
Order:
PROs
It's deterministic
CONs
It's greedy (optimization is done step by step and agglomeration decisions cannot be undone)
It's computationally expensive
Agglomerative clustering:
Agglomerative clustering: hyperparameters
- n_clusters : number of clusters
- affinity : the distance/similarity definition
- linkage : the scheme to measure distance to a cluster
- random_state : for reproducibility

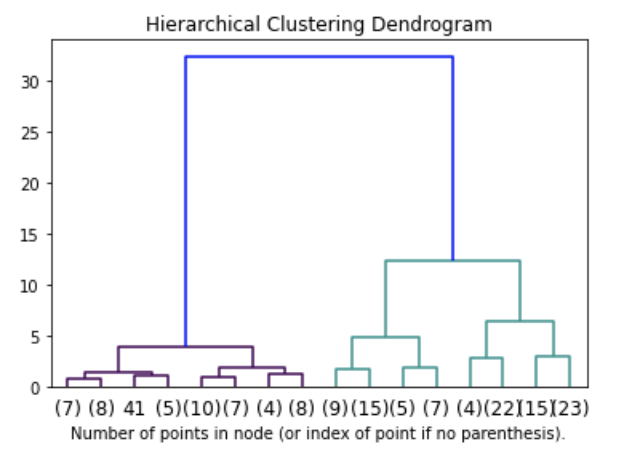
Agglomerative clustering: visualizing the dandrogram