Machine Learning for
Time Series Analysis XI
Neural Networks: FineTuning
Fall 2025 - UDel PHYS 664
dr. federica bianco

@fedhere

this slide deck:
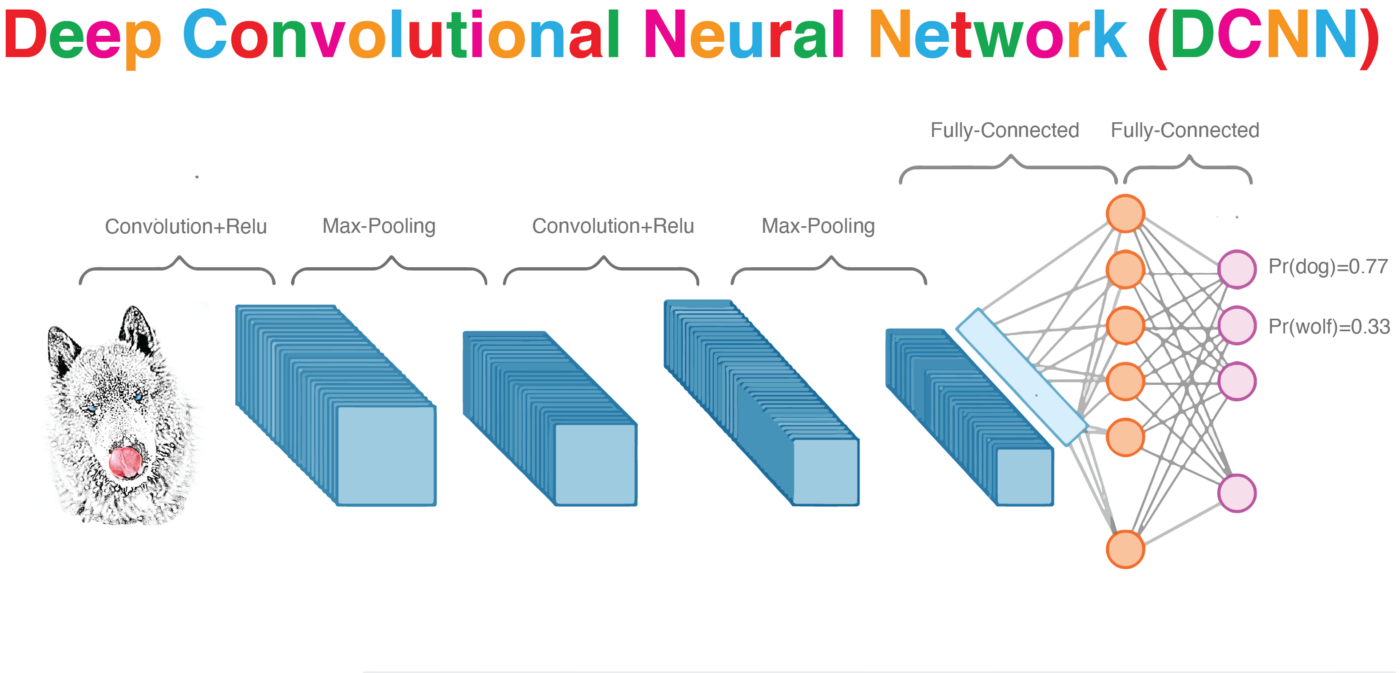
CNN
1
Convolutional Neural Nets
proper care of your DNN
0
NN are a vast topics and we only have 2 weeks!
Some FREE references!

michael nielsen
better pedagogical approach, more basic, more clear
ian goodfellow
mathematical approach, more advanced, unfinished
michael nielsen
better pedagogical approach, more basic, more clear

Lots of parameters and lots of hyperparameters! What to choose?
cheatsheet
-
architecture - wide networks tend to overfit, deep networks are hard to train
- number of epochs - the sweet spot is when learning slows down, but before you start overfitting... it may take DAYS! jumps may indicate bad initial choices (like in all gradient descent)
- loss function - needs to be appropriate to the task, e.g. classification vs regression
-
activation functions - needs to be consistent with the loss function
- optimization scheme - needs to be appropriate to the task and data
- learning rate in optimization - balance speed and accuracy
- batch size - smaller batch size is faster but leads to overtraining
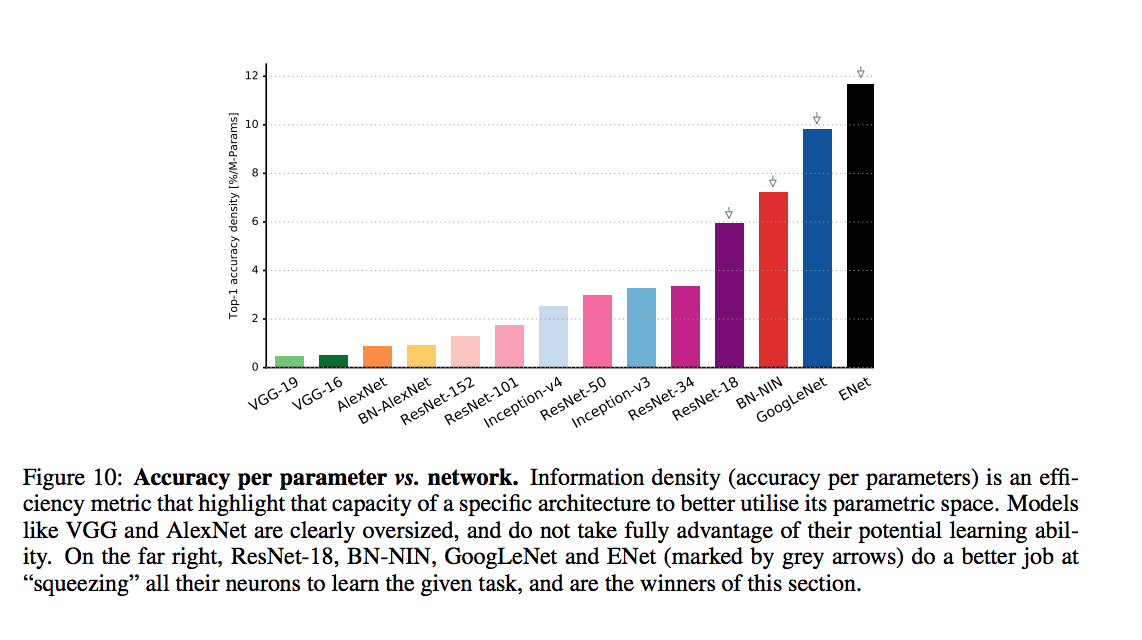
An article that compars various DNNs

An article that compars various DNNs

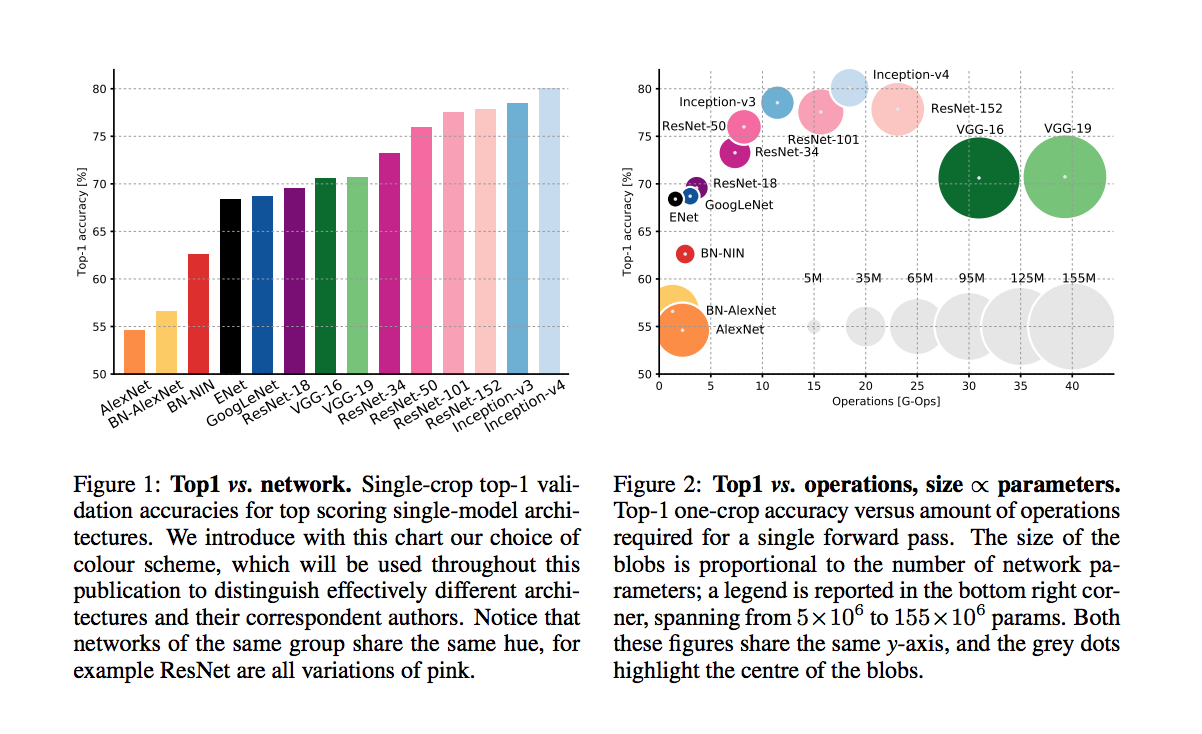
accuracy comparison
An article that compars various DNNs


accuracy comparison
An article that compars various DNNs

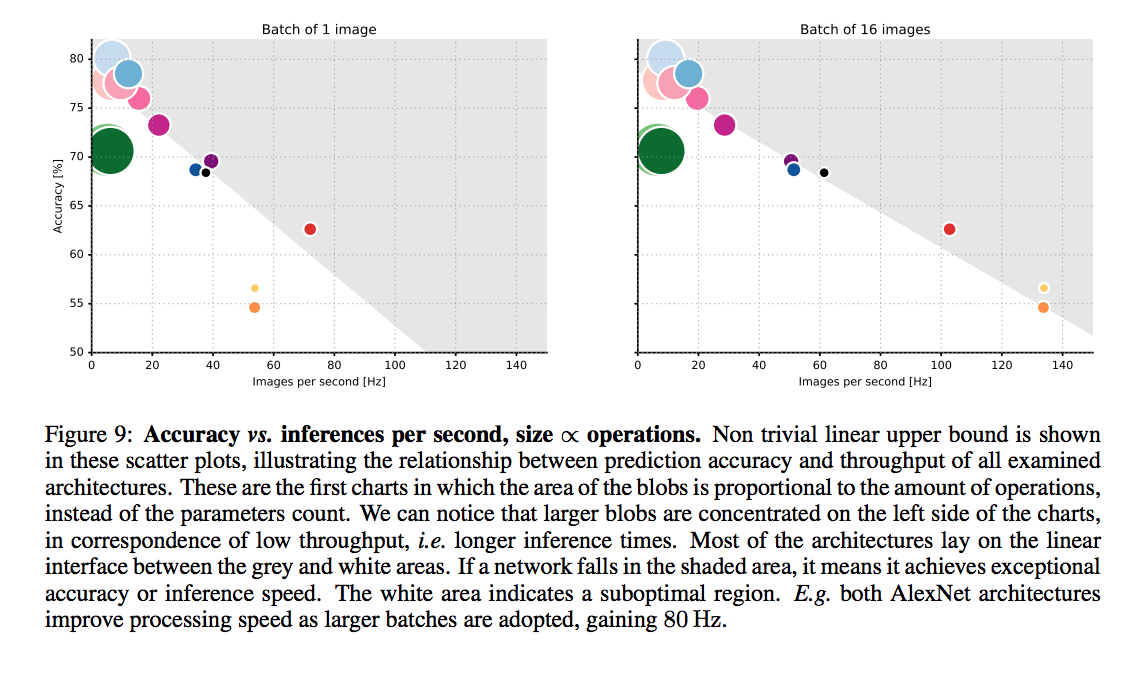
batch size

Lots of parameters and lots of hyperparameters! What to choose?
cheatsheet
- architecture - wide networks tend to overfit, deep networks are hard to train
-
number of epochs - the sweet spot is when learning slows down, but before you start overfitting... it may take DAYS! jumps may indicate bad initial choices
-
loss function - needs to be appropriate to the task, e.g. classification vs regression
-
activation functions - needs to be consistent with the loss function
- optimization scheme - needs to be appropriate to the task and data
- learning rate in optimization - balance speed and accuracy
- batch size - smaller batch size is faster but leads to overtraining


What should I choose for the loss function and how does that relate to the activation functiom and optimization?
Lots of parameters and lots of hyperparameters! What to choose?


What should I choose for the loss function and how does that relate to the activation functiom and optimization?
Lots of parameters and lots of hyperparameters! What to choose?

Lots of parameters and lots of hyperparameters! What to choose?
cheatsheet
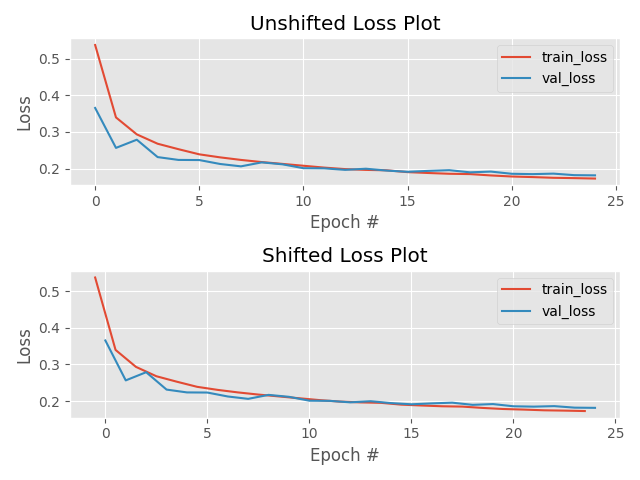
always check your loss function! it should go down smoothly and flatten out at the end of the training.
not flat? you are still learning!
too flat? you are overfitting...
loss (gallery of horrors)
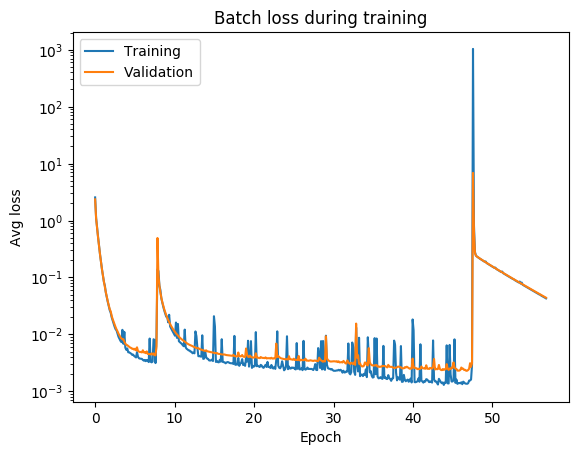
jumps are not unlikely (and not necessarily a problem) if your activations are discontinuous (e.g. relu)
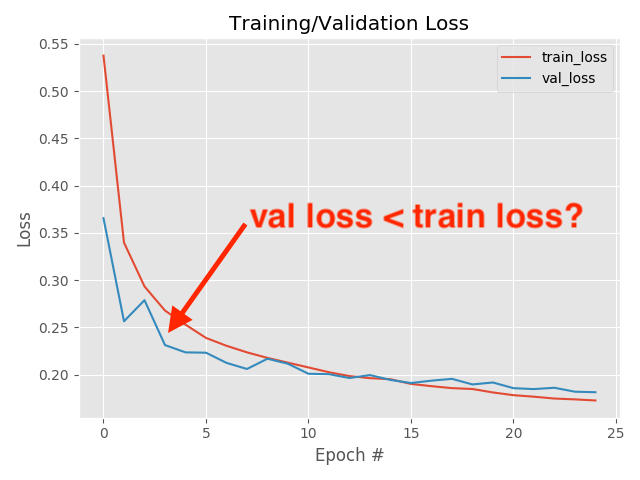
when you use validation you are introducing regularizations (e.g. dropout) so the loss can be smaller than for the training set
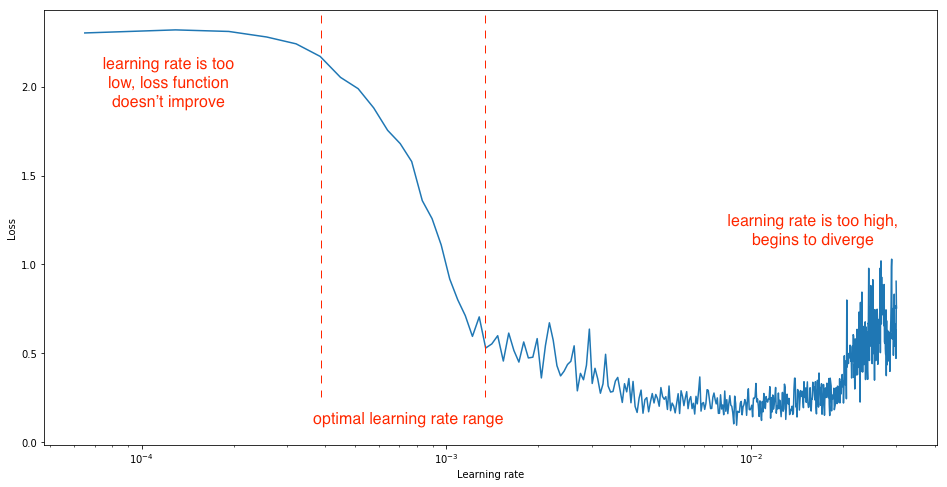
loss and learning rate (not that the appropriate learning rate depends on the chosen optimization scheme!)

Building a DNN
with keras and tensorflow
autoencoder for image recontstruction
What should I choose for the loss function and how does that relate to the activation functiom and optimization?
| loss | good for | activation last layer | size last layer |
|---|---|---|---|
| mean_squared_error | regression | linear | one node |
| mean_absolute_error | regression | linear | one node |
| mean_squared_logarithmit_error | regression | linear | one node |
| binary_crossentropy | binary classification | sigmoid | one node |
| categorical_crossentropy | multiclass classification | sigmoid | N nodes |
| Kullback_Divergence | multiclass classification, probabilistic inerpretation | sigmoid | N nodes |
On the interpretability of DNNs
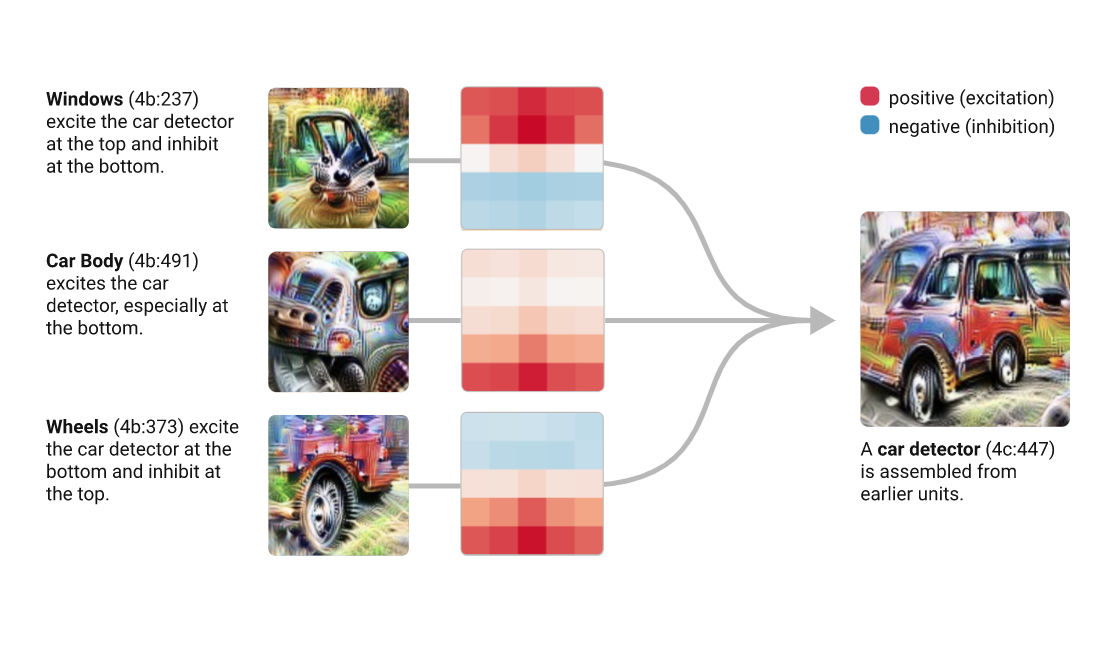



CNN


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


@akumadog
Brain Programming and the Random Search in Object Categorization


The visual cortex learns hierarchically: first detects simple features, then more complex features and ensembles of features
Convolution
convolution is a mathematical operator on two functions
f and g
that produces a third function
f x g
expressing how the shape of one is modified by the other.
o
two images.
| -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | |
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | -1 |
1
1
1
1
1
1
1
1
1
| -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| -1 | -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
1
1
1
1
1
| -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | |
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | -1 |
| -1 | -1 | 1 |
| -1 | 1 | -1 |
| 1 | -1 | -1 |
feature maps
1
1
1
1
1
convolution
| -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | |
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
1
1
1
1
1
| -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | |
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 7 | ||
|---|---|---|
=
1
1
1
1
1
| -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | |
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 7 | -3 | |
|---|---|---|
=
1
1
1
1
1
| -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | |
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 7 | -1 | 3 |
|---|---|---|
| ? | ||
=
1
1
1
1
1
| -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | |
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 7 | -1 | 3 |
|---|---|---|
| ? | ? | |
=
1
1
1
1
1
| -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | |
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 7 | -1 | 3 |
|---|---|---|
| ? | ? | |
=
1
1
1
1
1
| -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | |
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 7 | -3 | 3 |
| -3 | 5 | -3 |
| 3 | -1 | 7 |
=
input layer
feature map
convolution layer
the feature map is "richer": we went from binary to R
1
1
1
1
1
| -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | |
| -1 | -1 | -1 | ||
| -1 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | 1 |
| 7 | -3 | 3 |
| -3 | 5 | -3 |
| 3 | -1 | 7 |
=
input layer
feature map
convolution layer
the feature map is "richer": we went from binary to R
and it is reminiscent of the original layer
7
5
7
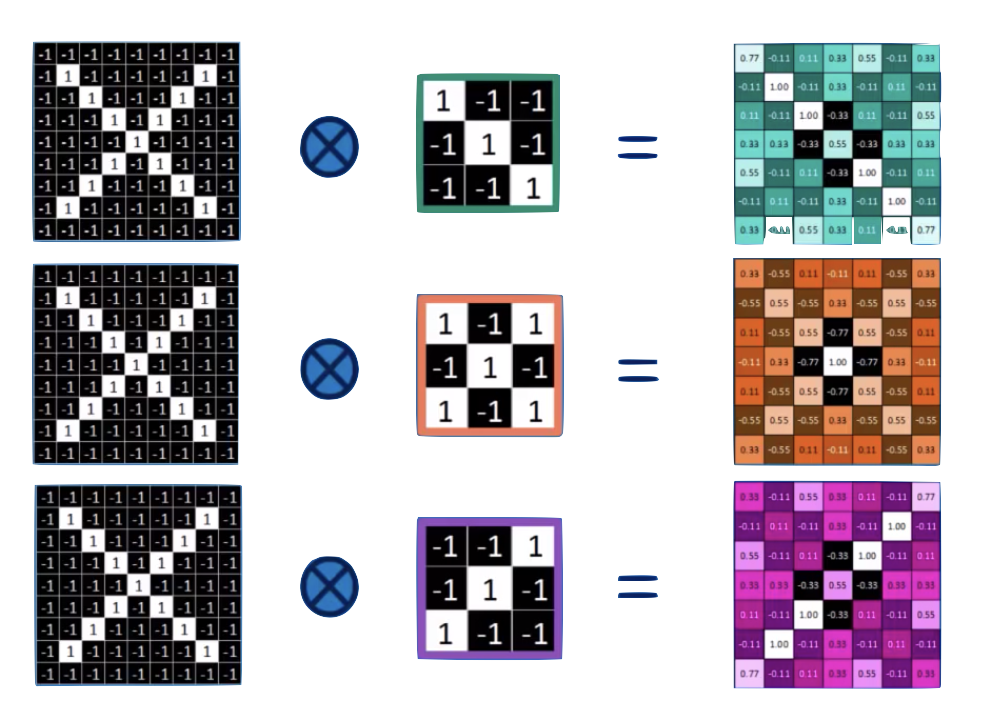
Convolve with different feature: each neuron is 1 feature
| 7 | -3 | 3 |
| -3 | 5 | -3 |
| 3 | -1 | 7 |
7
5
7
ReLu: normalization that replaces negative values with 0's
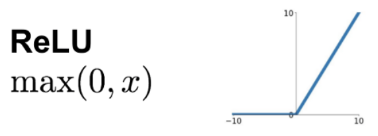
| 7 | 0 | 3 |
| 0 | 5 | 0 |
| 3 | 0 | 7 |
7
5
7
1c
Max-Pool
CNN
MaxPooling: reduce image size, generalizes result
| 7 | 0 | 3 |
| 0 | 5 | 0 |
| 0 | 0 | 7 |
7
5
7
MaxPooling: reduce image size, generalizes result
| 7 | 0 | 3 |
| 0 | 5 | 0 |
| 3 | 0 | 7 |
7
5
7
2x2 Max Poll
| 7 | 5 |
MaxPooling: reduce image size, generalizes result
| 7 | 0 | 3 |
| 0 | 5 | 0 |
| 3 | 0 | 7 |
7
5
7
2x2 Max Poll
| 7 | 5 |
| 5 |
MaxPooling: reduce image size, generalizes result
| 7 | 0 | 3 |
| 0 | 5 | 0 |
| 3 | 0 | 7 |
7
5
7
2x2 Max Poll
| 7 | 5 |
| 5 | 7 |
MaxPooling: reduce image size & generalizes result
By reducing the size and picking the maximum of a sub-region we make the network less sensitive to specific details
convolutional NN
deep dreams
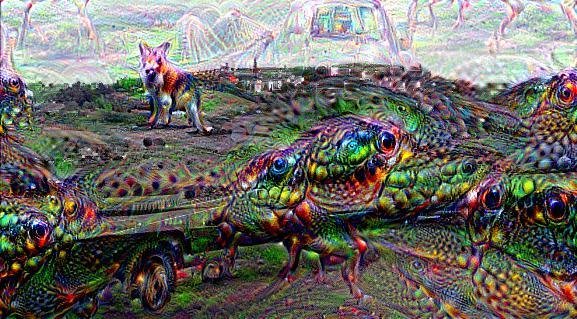
deep dreams

what is happening in DeepDream?
Deep Dream (DD) is a google software, a pre-trained NN (originally created on the Cafe architecture, now imported on many other platforms including tensorflow).
The high level idea relies on training a convolutional NN to recognize common objects, e.g. dogs, cats, cars, in images. As the network learns to recognize those objects is developes its layers to pick out "features" of the NN, like lines at a cetrain orientations, circles, etc.
The DD software runs this NN on an image you give it, and it loops on some layers, thus "manifesting" the things it knows how to recognize in the image.
Transfer Learning
can you use it for another task?
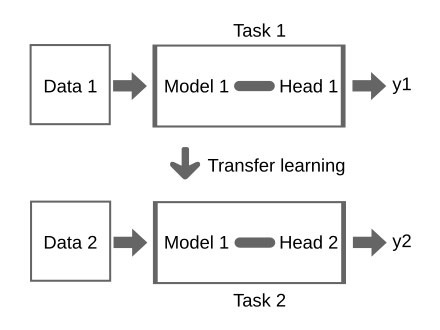
you have a model which was trained on some data
DOMAIN ADAPTATION: learning a model from a source data distribution and applying that model on a target data with a different distribution: the features are the same but have different distributions
e.g. Learn an energy model in one city (using building size, usage, occupancy) then apply it to a different city
?
Transfer Learning
does the model generalize to answer question on the new dataset with accuracy?
YES
NO
No need for additional learning: the model is transferable!
Fine Tune your model on the new data

you have a model which was trained on some data
Transfer Learning
What problems does it solve?
Small labelled dataset for supervised learning: use a model trained on a larger related dataset (and possibly fine tune with small amount of labels)
Limited computational resources because more are not available or to limit environmental impact of AI, as low level learning can be reused
knowledge learned from a task is re-used in order to boost performance on a related task.

you have a model which was trained on some data
Transfer Learning
What problems does it solve?
Small labelled dataset for supervised learning: use a model trained on a larger related dataset (and possibly fine tune with small amount of labels)
Limited computational resources because more are not available or to limit environmental impact of AI, as low level learning can be reused
knowledge learned from a task is re-used in order to boost performance on a related task.

you have a model which was trained on some data
Industry models like Chat-GPT or SAM are trained on huge amount of data we scientists could not afford to get!
Transfer Learning
What problems does it solve?
Small labelled dataset for supervised learning: use a model trained on a larger related dataset (and possibly fine tune with small amount of labels)
Limited computational resources because more are not available or to limit environmental impact of AI, as low level learning can be reused
knowledge learned from a task is re-used in order to boost performance on a related task.

you have a model which was trained on some data
And large companies like Open-AI, Facebook, Google have unmatched computational resources

Fine-tuning by retraining everything for few epochs (few 10)
Start with the saved trained model:
weights and biases are set in the pre-trained model by training on Data 1
restart training from those weights and biases and adjust weights by running only a few epochs
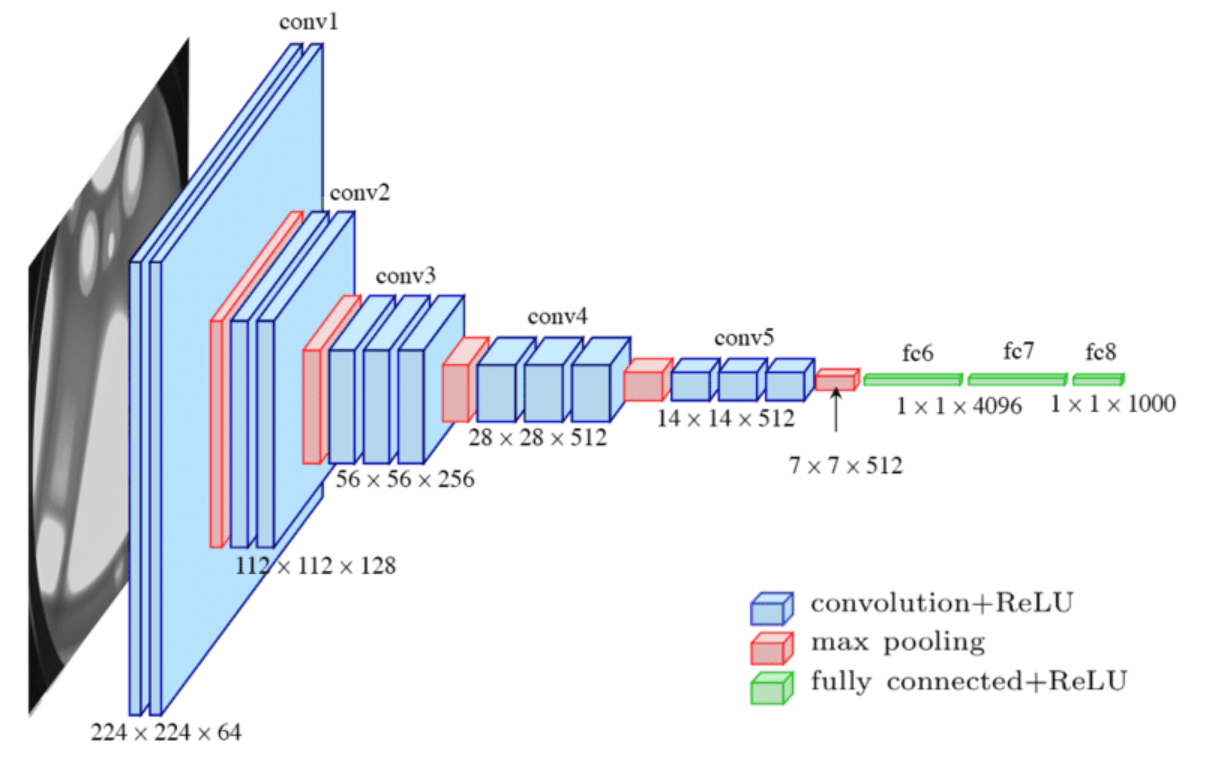
prediction "head"
original data
fine tuning

Remember the "Deep Dream" demo and assignment
prediction "head"

early layers learn simple generalized features (like lines for CNN)
original data
fine tuning

Remember the "Deep Dream" demo and assignment


early layers learn simple generalized features (like lines for CNN)
prediction "head"
original data
fine tuning


late layers learn complex aggregate specialized features
fine tuning
Remember the "Deep Dream" demo and assignment


early layers learn simple generalized features (like lines for CNN)
prediction "head"
original data


late layers learn complex aggregate specialized features
Limited training - fine tuning
Remember the "Deep Dream" demo and assignment
Retrain (late layers and) head

Replace input
prediction "head"
- Start with the weights as trained on the original dataset
- Train for a few epochs (sometimes as few as 10!)
The issue of vanishing gradient persists, but in this case it's helpful as it means we are mostly training the specialized layers at the end of the NN structure
- Makes large models accessible even if each training epoch is expensive by limiting the number of training epochs needed
- All rules of training need to be respected, including checking loss, adjusting learning rate, batch size (appropriately to the new dataset) etc


late layers learn complex aggregate specialized features
"Chop the head" fine tuning
Remember the "Deep Dream" demo and assignment

Replace input


early layers learn simple generalized features (like lines for CNN)
prediction "head"


late layers learn complex aggregate specialized features
"Chop the head" fine tuning
Remember the "Deep Dream" demo and assignment
"Freeze" early layers

Replace input
prediction "head"


late layers learn complex aggregate specialized features
"Chop the head" fine tuning
Remember the "Deep Dream" demo and assignment
"Freeze" early layers
Retrain (late layers and) head

Replace input
prediction "head"
Can also modify the prediction head to change the scope of the NN (e.g. from classification to regression)
Fine-tuning how to:
layer = keras.layers.Dense(3)
layer.build((None, 4)) # Create the weights
print("weights:", len(layer.weights))
print("trainable_weights:", len(layer.trainable_weights))
print("non_trainable_weights:", len(layer.non_trainable_weights))
layer = keras.layers.Dense(3)
layer.build((None, 4)) # Create the weights
layer.trainable = False # Freeze the layer
print("weights:", len(layer.weights))
print("trainable_weights:", len(layer.trainable_weights))
print("non_trainable_weights:", len(layer.non_trainable_weights))
Fine-tuning how to:
layer = keras.layers.Dense(3)
layer.build((None, 4)) # Create the weights
print("weights:", len(layer.weights))
print("trainable_weights:", len(layer.trainable_weights))
print("non_trainable_weights:", len(layer.non_trainable_weights))
layer = keras.layers.Dense(3)
layer.build((None, 4)) # Create the weights
layer.trainable = False # Freeze the layer
print("weights:", len(layer.weights))
print("trainable_weights:", len(layer.trainable_weights))
print("non_trainable_weights:", len(layer.non_trainable_weights))

for name, parameter in model.named_parameters():
if not name.startswith(layernameroot):
#print("here", name)
parameter.requires_grad = Falseparameter.requires_grad = False(some models are really only available in pytorch ATM)
layer.trainable = False


Fine-tuning SAM example:
from segment_anything import sam_model_registry, SamAutomaticMaskGenerator, SamPredictor
from torch.utils.data import DataLoader
from torchvision import transforms
from torchvision.transforms import Resize
from PIL import Image
import torch
import torch.nn.functional as F
import os
import cv2
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
sam = sam_model_registry["vit_h"](checkpoint="sam_vit_h_4b8939.pth")
sam.to(device=device)
mask_generator = SamAutomaticMaskGenerator(sam)
.....
from prettytable import PrettyTable
def count_parameters(model):
table = PrettyTable(['Modules', 'Parameters'])
total_params = 0
for name, parameter in model.named_parameters():
if not parameter.requires_grad: continue
params = parameter.numel()
table.add_row([name, params])
total_params+=params
print(table)
print(f'Total Trainable Params: {total_params}')
return total_paramsloading a saved model
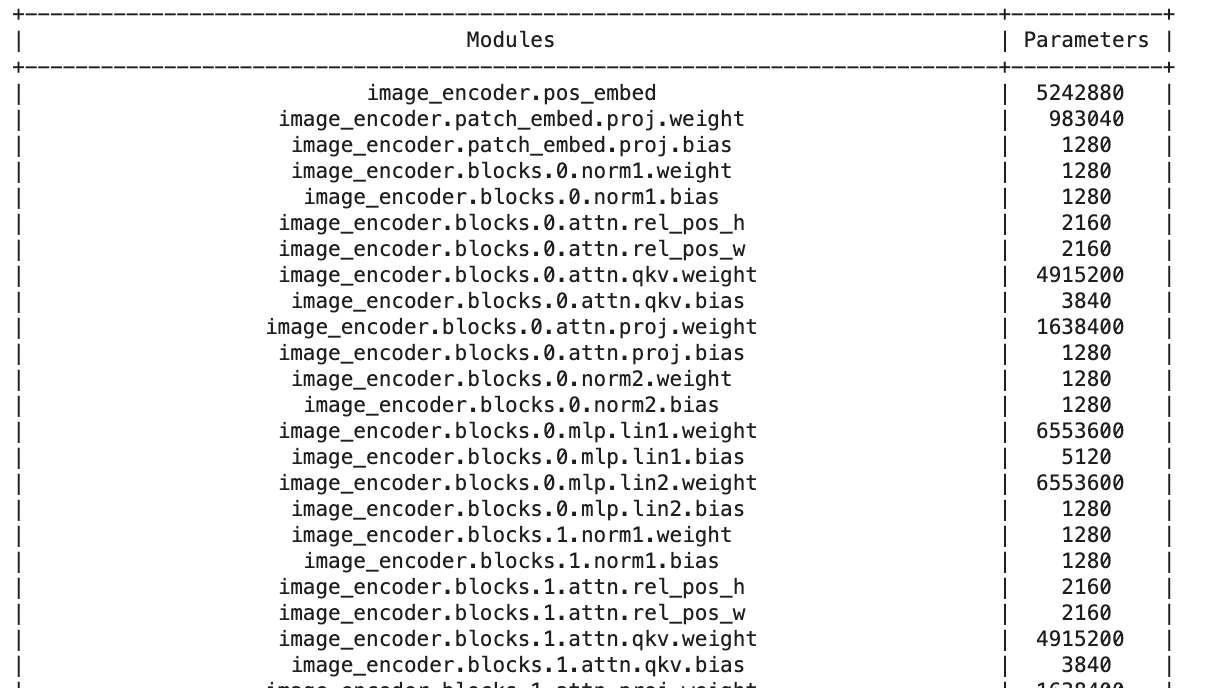
prints the number of parameters for every layer
Fine-tuning SAM example:
from prettytable import PrettyTable
def count_trainablelayers(model):
trainable = 0
table = PrettyTable(['Modules', 'Gradient'])
for name, parameter in model.named_parameters():
table.add_row([name, parameter.requires_grad])
trainable +=1
print(table)
return trainable
count_trainablelayers(sam) # this gives 596!!
checks if "gradient=true" i.e. if weights are trainable
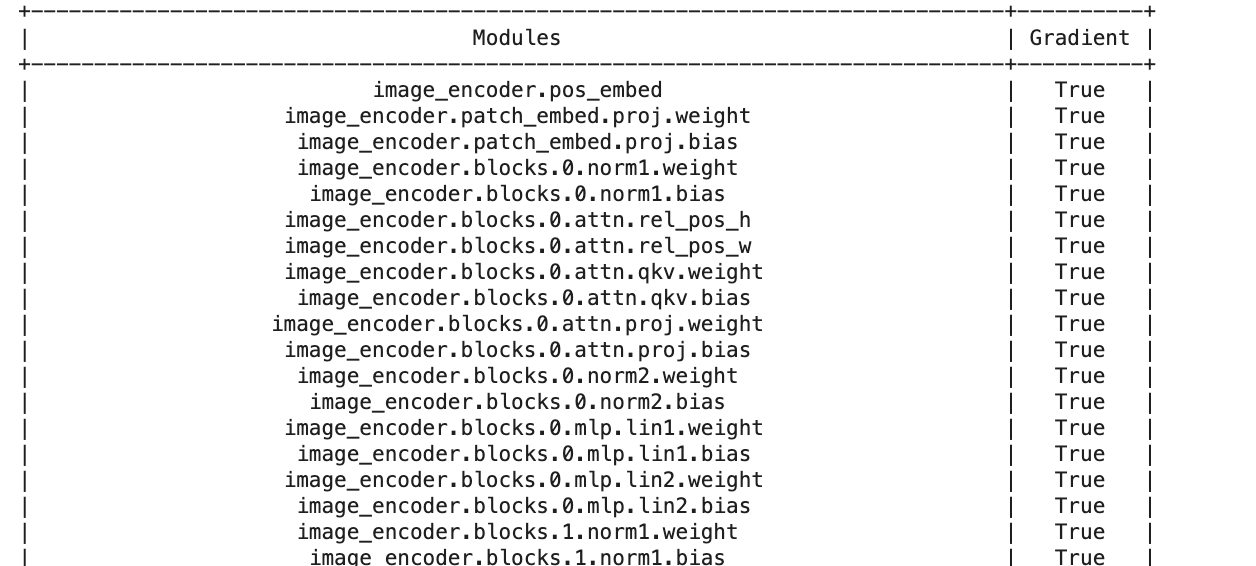
Fine-tuning SAM example:
from prettytable import PrettyTable
def count_trainablelayers(model):
trainable = 0
table = PrettyTable(['Modules', 'Gradient'])
for name, parameter in model.named_parameters():
table.add_row([name, parameter.requires_grad])
trainable +=1
print(table)
return trainable
count_trainablelayers(sam) # this gives 596!!
def freeze_layer(model, layernameroot):
trainable = 0
table = PrettyTable(['Modules', 'Gradient'])
for name, parameter in model.named_parameters():
if not name.startswith(layernameroot):
#print("here", name)
parameter.requires_grad = False
table.add_row([name, parameter.requires_grad])
if parameter.requires_grad:
trainable +=1
print(table)
return trainable
ntrainable = freeze_layer(sam, 'mask_decoder.iou_prediction_head')
torch.save(model.state_dict(), f"samLE_funfrozen{ntrainable}.pth")checks if "gradient=true" i.e. if weights are trainable

sets gradient to false i.e. freezes the layer
Fine-tuning SAM example:
Fine-tuning SAM example:
from prettytable import PrettyTable
def count_trainablelayers(model):
trainable = 0
table = PrettyTable(['Modules', 'Gradient'])
for name, parameter in model.named_parameters():
table.add_row([name, parameter.requires_grad])
trainable +=1
print(table)
return trainable
count_trainablelayers(sam) # this gives 596!!
def freeze_layer(model, layernameroot):
trainable = 0
table = PrettyTable(['Modules', 'Gradient'])
for name, parameter in model.named_parameters():
if not name.startswith(layernameroot):
#print("here", name)
parameter.requires_grad = False
table.add_row([name, parameter.requires_grad])
if parameter.requires_grad:
trainable +=1
print(table)
return trainable
ntrainable = freeze_layer(sam, 'mask_decoder.iou_prediction_head')
torch.save(model.state_dict(), f"samLE_funfrozen{ntrainable}.pth")sets gradient to false i.e. freezes the layer


... only the "head" is left to be trainable