Machine Learning for
Time Series Analysis X
Neural Networks: RNNs, LSTM
Fall 2022 - UDel PHYS 667
dr. federica bianco

@fedhere


this slide deck:

Deep Learning
1
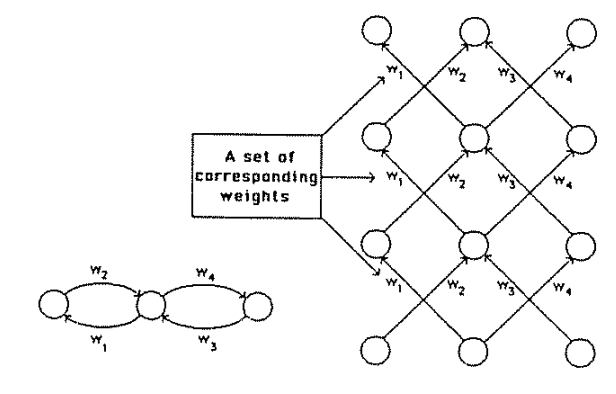
MLTSA:

what we are doing, except for the activation function
is exactly a series of matrix multiplictions.

3x5
5x2
2x1
=
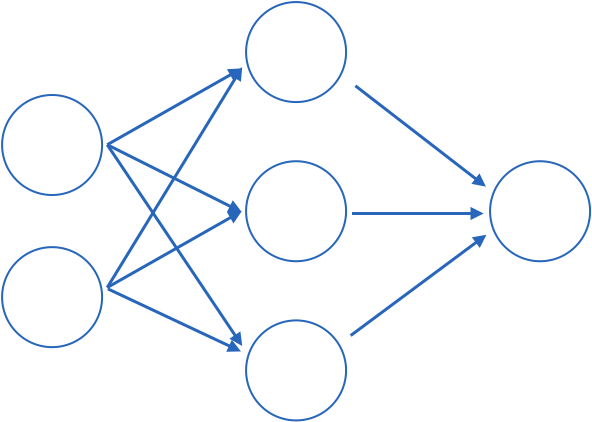
DeepNeuralNetwork
DeepNeuralNetwork
The purpose is to approximate a function φ
y = φ(x)
which (in general) is not linear with linear operations
what we are doing, except for the activation function
is exactly a series of matrix multiplictions.
DeepNeuralNetwork
The purpose is to approximate a function φ
y = φ(x)
which (in general) is not linear with linear operations

Building a DNN
with keras and tensorflow
autoencoder for image recontstruction
What should I choose for the loss function and how does that relate to the activation functiom and optimization?
| loss | good for | activation last layer | size last layer |
|---|---|---|---|
| mean_squared_error | regression | linear | one node |
| mean_absolute_error | regression | linear | one node |
| mean_squared_logarithmit_error | regression | linear | one node |
| binary_crossentropy | binary classification | sigmoid | one node |
| categorical_crossentropy | multiclass classification | sigmoid | N nodes |
| Kullback_Divergence | multiclass classification, probabilistic inerpretation | sigmoid | N nodes |
Text
DeepNeuralNetwork - loss functions
Binary Cross Entropy
(Multiclass) Cross Entropy
c = class
o = object
p = probability
y = label | truth
y = prediction
Kullback-Leibler
(Multiclass) Cross Entropy
Mean Squared Error
Mean Absolute Error
Mean Squared Logarithmic Error
^
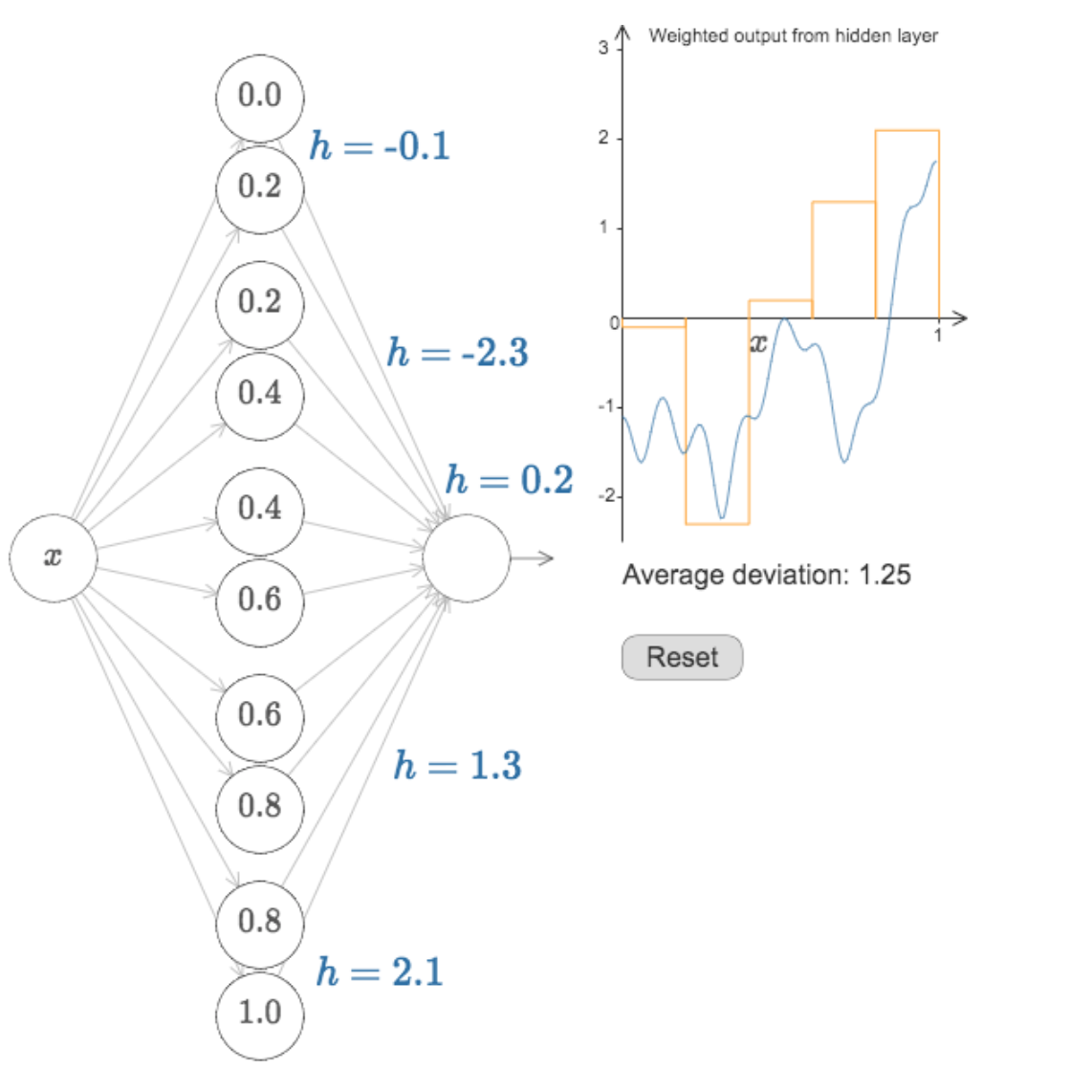
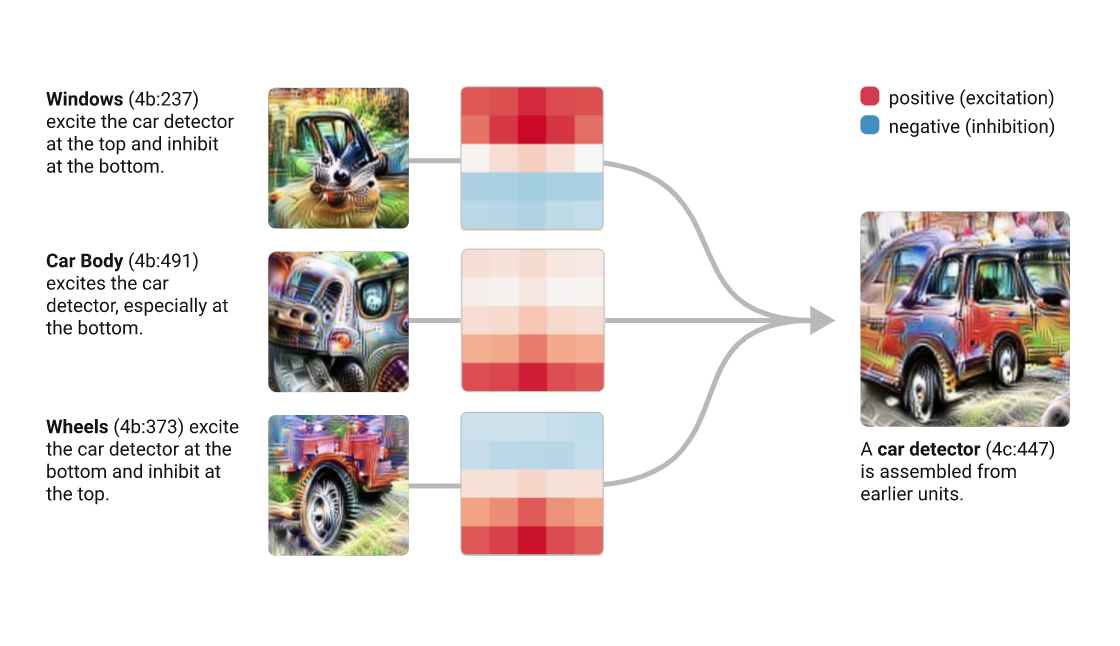
On the interpretability of DNNs



MLTSA:
training DNN
2
.
.
.
Any linear model:
y : prediction
ytrue : target
Error: e.g.
intercept
slope
L2
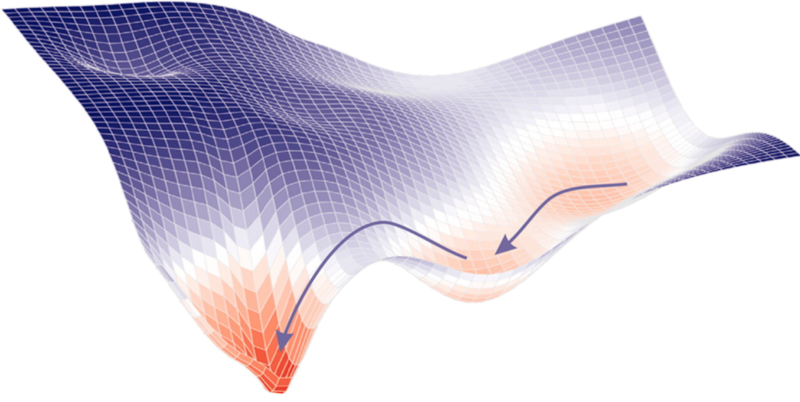
Find the best parameters by finding the minimum of the L2 hyperplane
at every step look around and choose the best direction
Gradient Descent
.
.
.
Any linear model:
y : prediction
ytrue : target
Error: e.g.
intercept
slope
L2
Find the best parameters by finding the minimum of the L2 hyperplane
at every step look around and choose the best direction
Gradient Descent

.
.
.
Any linear model:
y : prediction
ytrue : target
Error: e.g.
intercept
slope
L2
Find the best parameters by finding the minimum of the L2 hyperplane
at every step look around and choose the best direction
Gradient Descent

new position
.
.
.
Any linear model:
y : prediction
ytrue : target
Error: e.g.
intercept
slope
L2
Find the best parameters by finding the minimum of the L2 hyperplane
at every step look around and choose the best direction
Gradient Descent

old position
.
.
.
Any linear model:
y : prediction
ytrue : target
Error: e.g.
intercept
slope
L2
Find the best parameters by finding the minimum of the L2 hyperplane
at every step look around and choose the best direction
Gradient Descent

gradient at the old position
.
.
.
Any linear model:
y : prediction
ytrue : target
Error: e.g.
intercept
slope
L2
Find the best parameters by finding the minimum of the L2 hyperplane
at every step look around and choose the best direction
Gradient Descent

learning rate
.
.
.
Any linear model:
Error: e.g.
Gradient Descent
learning rate
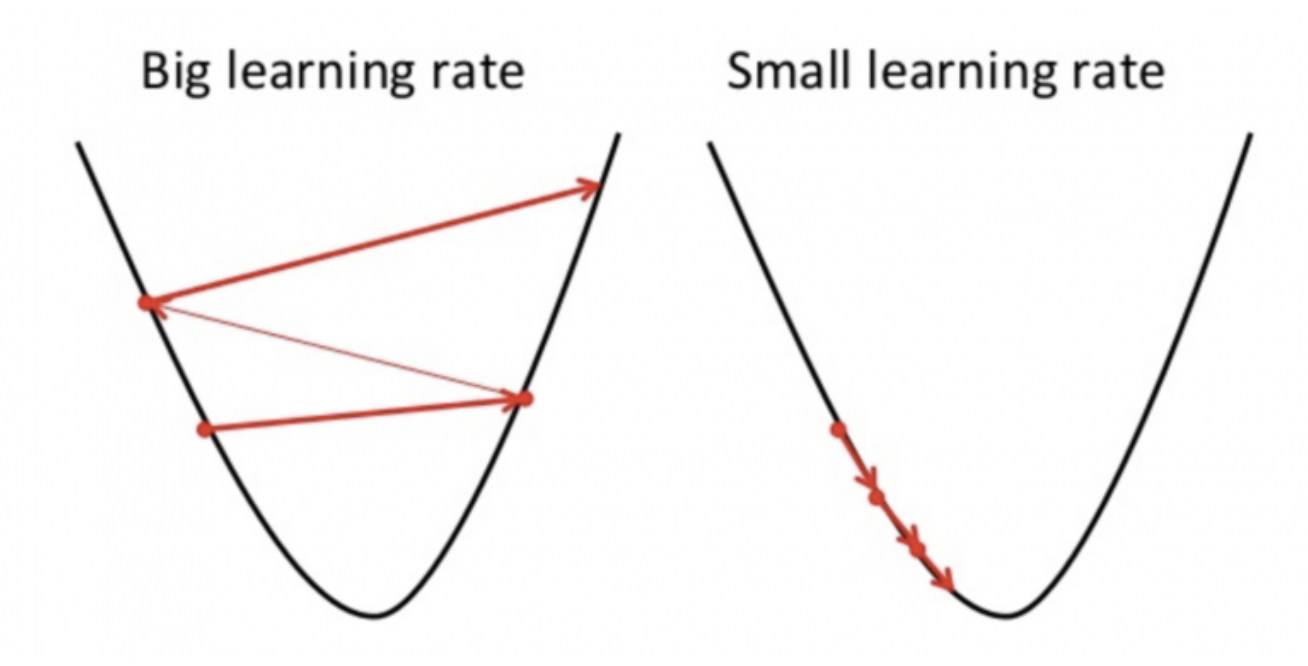
adaptive lr
back-propagation

how does linear descent look when you have a whole network structure with hundreds of weights and biases to optimize??
.
.
.
output

Training models with this many parameters requires a lot of care:
. defining the metric
. optimization schemes
. training/validation/testing sets
But just like our simple linear regression case, small changes in the parameters lead to small changes in the output for the right activation functions.
define a cost function, e.g.
x1
x2
b1
b2
b3
b
w11
w12
w13
w21
w22
w23

Training models with this many parameters requires a lot of care:
. defining the metric
. optimization schemes
. training/validation/testing sets
But just like our simple linear regression case, small changes in the parameters lead to small changes in the output for the right activation functions.
define a cost function, e.g.

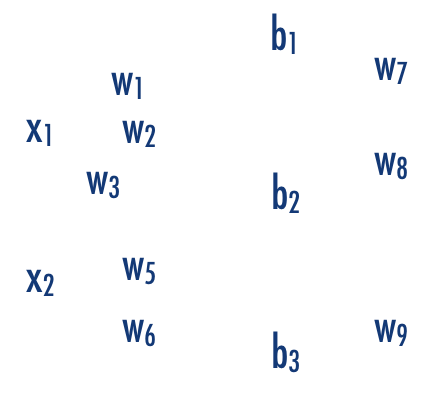

Training models with this many parameters requires a lot of care:
. defining the metric
. optimization schemes
. training/validation/testing sets
But just like our simple linear regression case, the fact that small changes in the parameters leads to small changes in the output for the right activation functions.
define a cost function, e.g.
Training models with this many parameters requires a lot of care:
. defining the metric
. optimization schemes
. training/validation/testing sets
But just like our simple linear regression case, the fact that small changes in the parameters leads to small changes in the output for the right activation functions.
define a cost function, e.g.
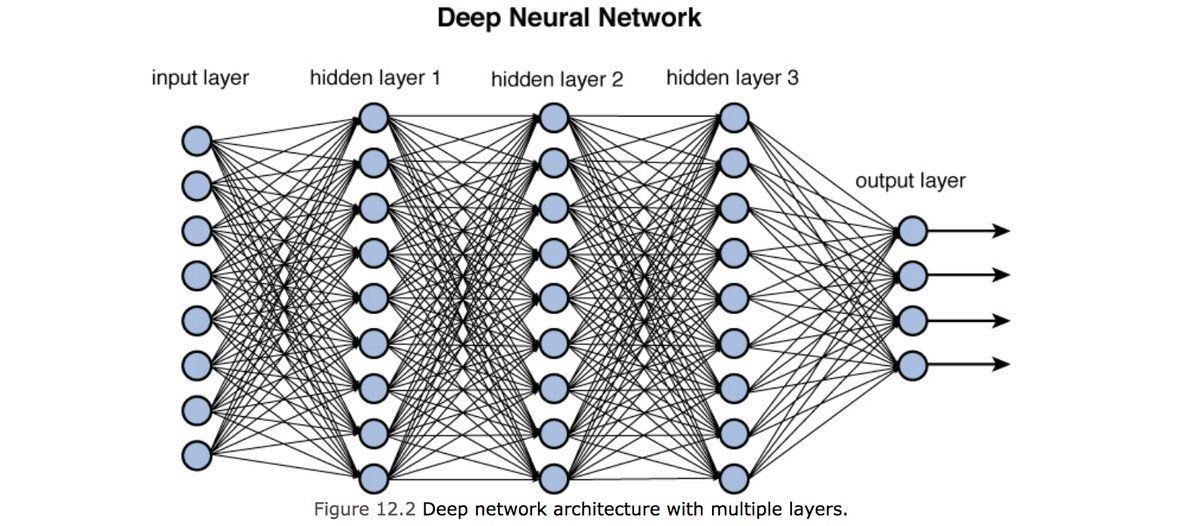
Training a DNN
feed data forward through network and calculate cost metric
for each layer, calculate effect of small changes on next layer
back-propagation
how does linear descent look when you have a whole network structure with hundreds of weights and biases to optimize??
think of applying just gradient to a function of a function of a function... use:
1) partial derivatives, 2) chain rule

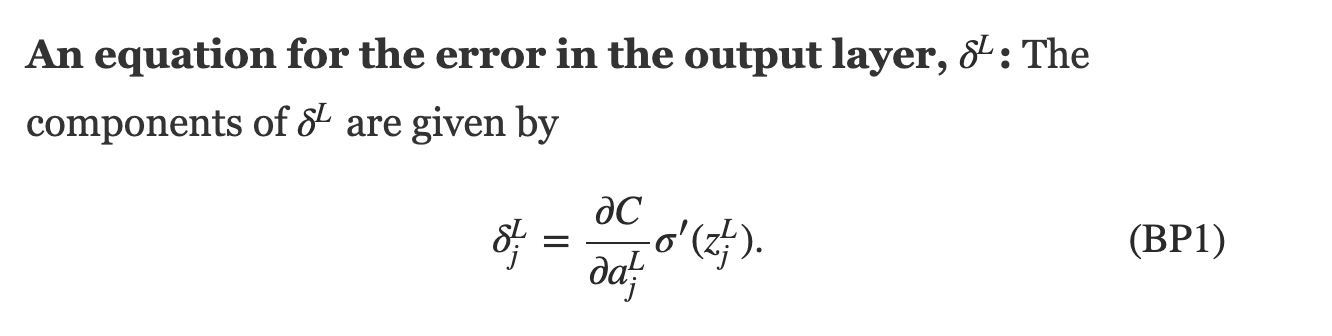

define a cost function, e.g.
Training a DNN
at every step look around and choose the best direction
Gradient Descent
Gradient Descent
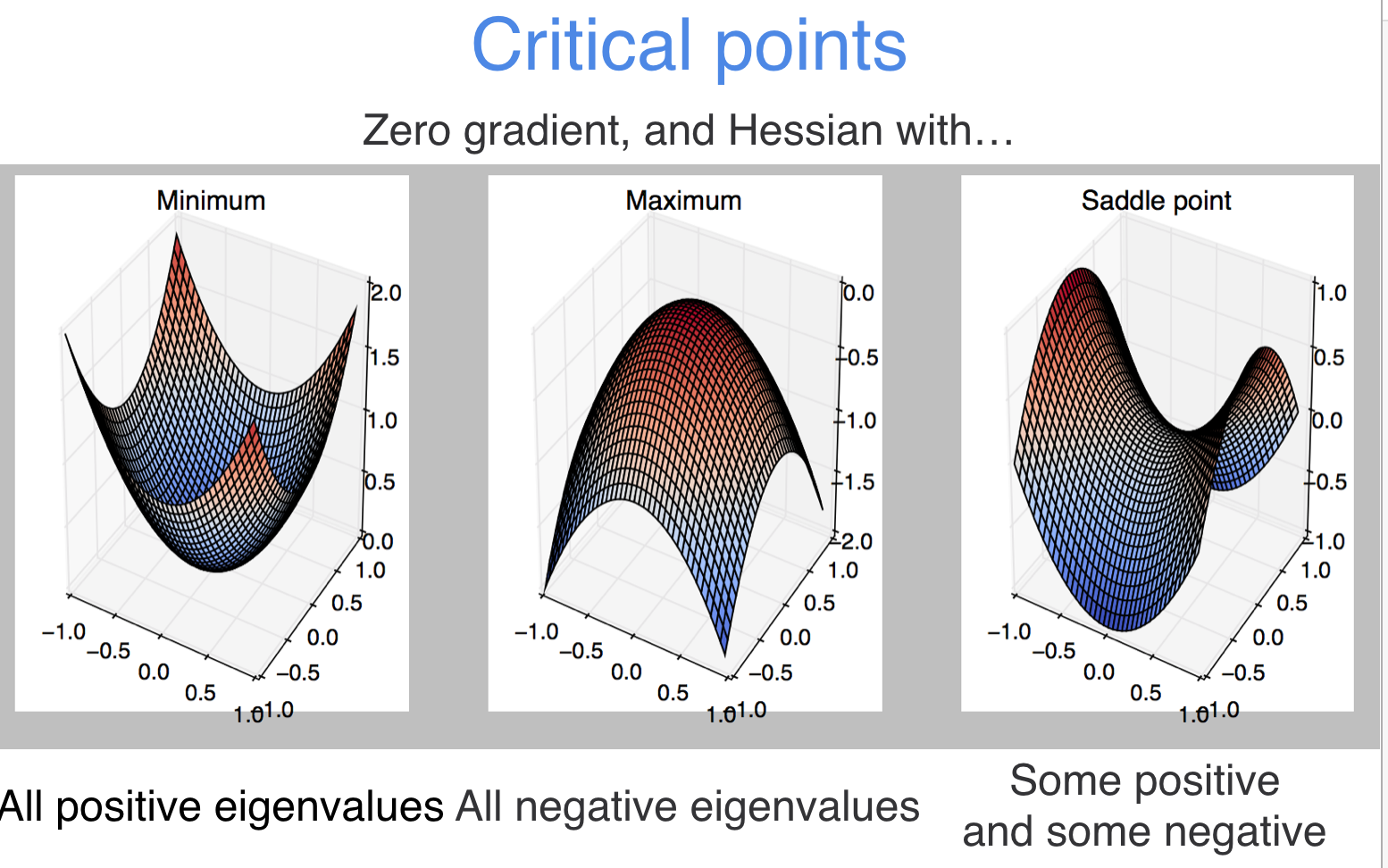
why do we not worry about local minima?
why do we not worry about local minima?
the course of dimensionality actually is a blessing here!
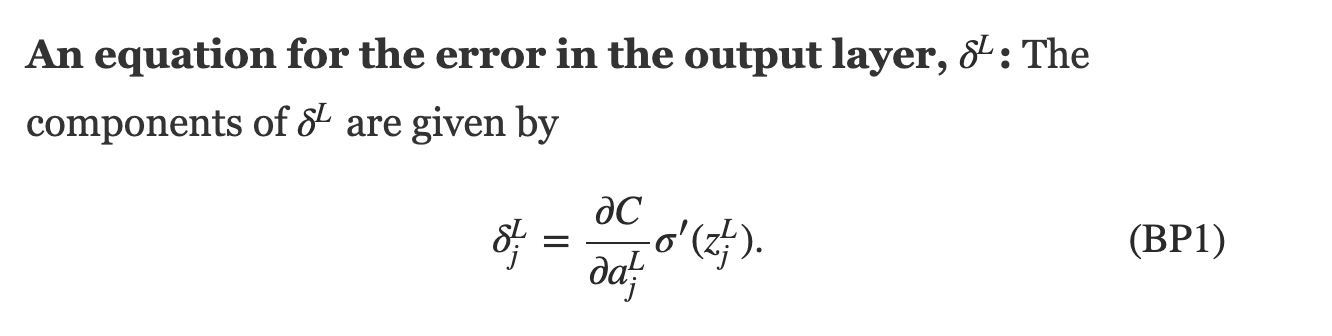
Training a DNN


1994
An time-domain enabled AI system should:
Training a DNN

you need to pick


1994
Training a DNN
you need to pick
Training a DNN



1994
We show why gradient based learning algorithms face an increasingly dicult problem as the duration of the dependencies to be captured increases
the magnitude of the derivative of the state of a dynamical system at time t with respect to the state at time 0 decreases exponentially as t increases.
We show why gradient based learning algorithms face an increasingly dicult problem as the duration of the dependencies to be captured increases
you need to pick
Training a DNN
you need to pick
Training a DNN


1994


MLTSA:
RNN
3

RNN architecture
input layer
output layer
hidden layers
Feed-forward NN architecture

RNN architecture
output layer
hidden layers
Feed-forward NN architecture
Recurrent NN architecture
input layer
output layer
RNN hidden layers

output layer
hidden layers
input layer
RNN architecture
input layer
output layer
RNN hidden layers


current state
previous state
Remember the state-space problem!
we want process a sequence of vectors x applying a recurrence formula at every time step:
RNN architecture
input layer
output layer
RNN hidden layers


Remember the state-space problem!
we want process a sequence of vectors x applying a recurrence formula at every time step:
current state
previous state
features
(can be time dependent)
function with parameters q
MLTSA:
state space model (from week ~4)
A State-space model is a model to derive the value of a time-dependent variable x(t), the state, generated by a noisy Markovian process, from observations of a variable y(t), also subject to noise, linearly related to the target variable
Definition
RNN architecture
input layer
output layer
RNN hidden layers


Simplest possible RNN
Whh
Wxh
Qhy
RNN architecture
input layer
output layer
RNN hidden layers


Simplest possible RNN
Whh
Wxh
Qhy
RNN architecture
input layer

Alternative graphical representation of RNN
h(t-1)
h(t)
h(t+1)
h(t+2)
h(t+3)
h(t+4)
y(t)
y(t+1)
y(t+2)
y(t+4)
y(t+3)
y(t+5)
Why
Why
Why
Why
Why
Whh
Whh
Whh
Whh
Whh
Wxh
the weights are the same! always the same Whh and Why
RNN architecture

appllications
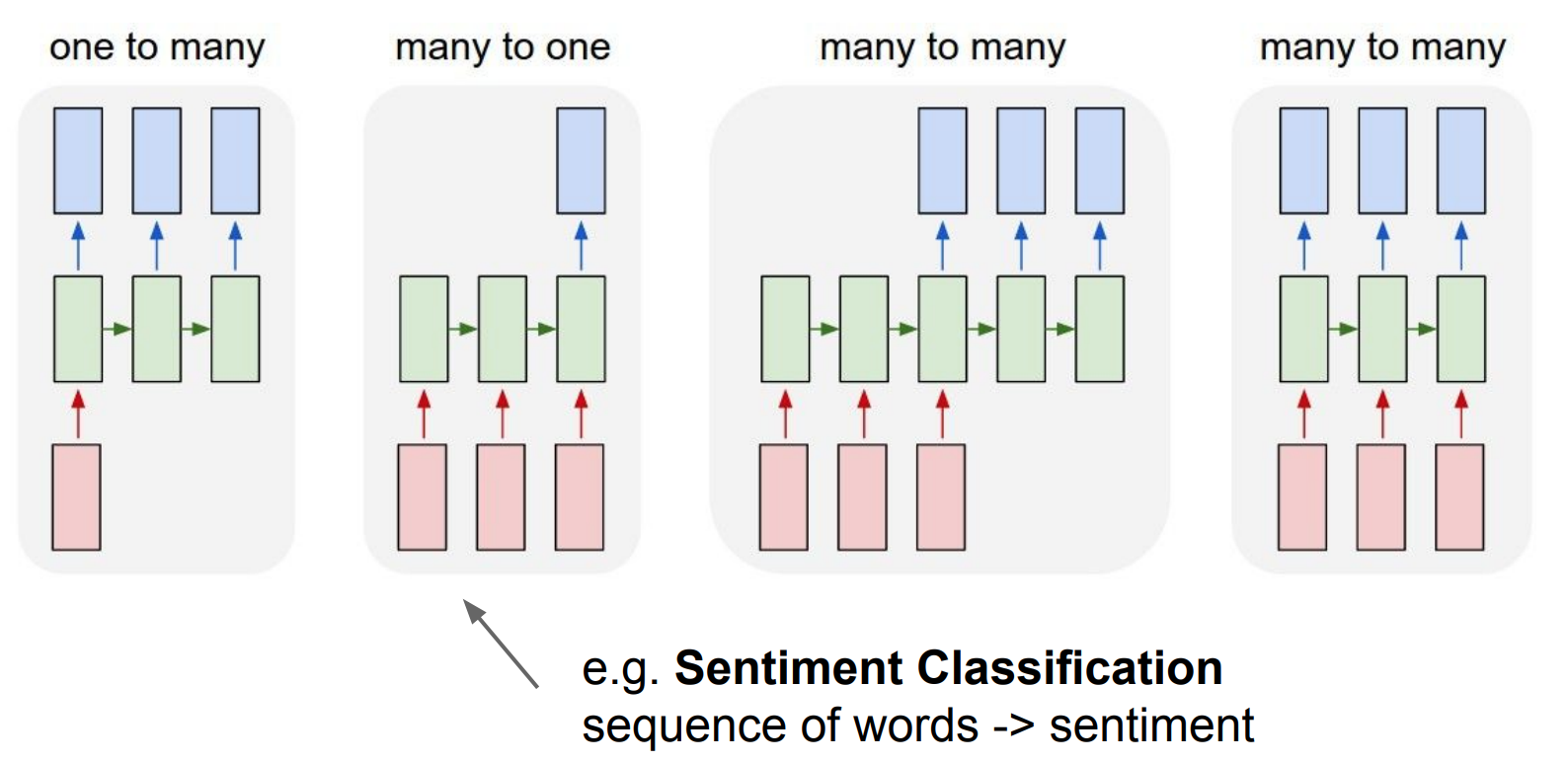
image captioning:
one image to a
sequence of words
RNN architecture

appllications

image captioning:
one image to a
sequence of words
sentiment analysis
sequence of words to one sentiment
RNN architecture

appllications

image captioning:
one image to a
sequence of words
sentiment analysis
sequence of words to one sentiment
language translator
sequence of words to sequence of words
RNN architecture

appllications

image captioning:
one image to a
sequence of words
sentiment analysis
sequence of words to one sentiment
language translator
sequence of words to sequence of words
online: video classification frame by frame
RNN architecture

more complicated RNNs
Some layers will be recurrent, others will not. Does not need to be fully connected
RNN architecture
input layer
e(t)
h(t-1)
h(t)
h(t+1)
h(t+2)
h(t+3)
h(t+4)
y(t)
y(t+1)
y(t+2)
y(t+4)
y(t+3)
y(t+5)
Why
Why
Why
Why
Why
Whh
Whh
Whh
Whh
Whh
Wxh
each output has its own loss
Why
e(t+1)
e(t+2)
e(t+3)
e(t+4)
e(t+5)
RNN architecture
input layer
e(t)
h(t-1)
h(t)
h(t+1)
h(t+2)
h(t+3)
h(t+4)
y(t)
y(t+1)
y(t+2)
y(t+4)
y(t+3)
y(t+5)
Why
Why
Why
Why
Why
Whh
Whh
Whh
Whh
Whh
Wxh
each output has its own loss
Why
e(t+1)
e(t+2)
e(t+3)
e(t+4)
e(t+5)
The cats that ate were full
The cat that ate was full
RNN architecture
input layer
e(t)
h(t-1)
h(t)
h(t+1)
h(t+2)
h(t+3)
h(t+4)
y(t)
y(t+1)
y(t+2)
y(t+4)
y(t+3)
y(t+5)
Why
Why
Why
Why
Why
Whh
Whh
Whh
Whh
Whh
Wxh
each output has its own loss
Why
e(t+1)
e(t+2)
e(t+3)
e(t+4)
e(t+5)
LOSS
RNN architecture
input layer
e(t)
h(t-1)
h(t)
h(t+1)
h(t+2)
h(t+3)
h(t+4)
y(t)
y(t+1)
y(t+2)
y(t+4)
y(t+3)
y(t+5)
Why
Why
Why
Why
Why
Whh
Whh
Whh
Whh
Whh
Wxh
each output has its own loss
Why
e(t+1)
e(t+2)
e(t+3)
e(t+4)
e(t+5)
Total loss:
RNN architecture
input layer
h(t-1)
h(t)
h(t+1)
h(t+2)
h(t+3)
h(t+4)
y(t)
y(t+1)
y(t+2)
y(t+4)
y(t+3)
Why
Why
Why
Why
Why
Whh
Whh
Whh
Whh
Whh
Wxh
each output has its own loss
Why
Total loss:
e(t)
y(t+5)
e(t+1)
e(t+2)
e(t+3)
e(t+4)
e(t+5)
RNN architecture
input layer
h(t-1)
h(t)
h(t+1)
h(t+2)
h(t+3)
h(t+4)
y(t)
y(t+1)
y(t+2)
y(t+4)
y(t+3)
Why
Why
Why
Why
Why
Whh
Whh
Whh
Whh
Whh
Wxh
each output has its own loss
Why
Total loss:
e(t)
y(t+5)
e(t+1)
e(t+2)
e(t+3)
e(t+4)
e(t+5)
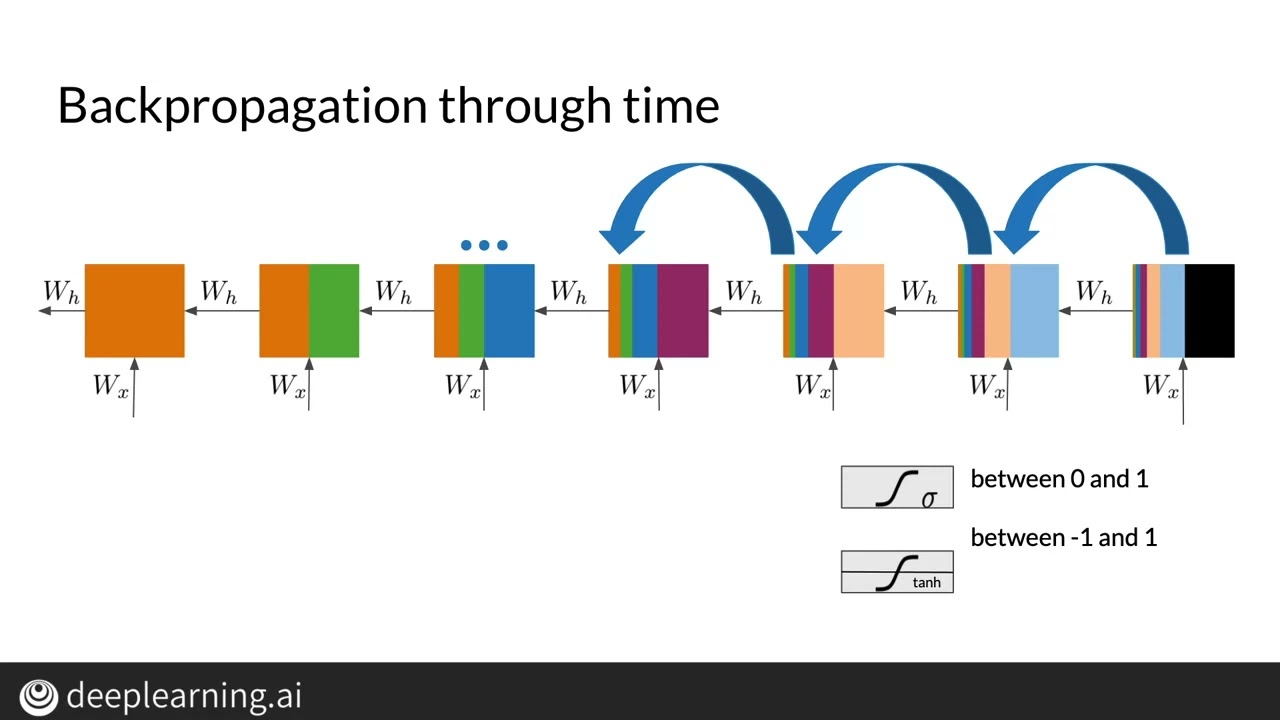
RNN architecture
vanishing gradient problem!
input layer
h(t-1)
h(t)
h(t+1)
h(t+2)
h(t+3)
h(t+4)
y(t)
y(t+1)
y(t+2)
y(t+4)
y(t+3)
y(t+5)
Why
Why
Why
Why
Why
Whh
Whh
Whh
Whh
Whh
Wxh
Why

Learns Fast!
Learns slow!


RNN
obsesses
over
recent
past
forgets
remote
past
vanishing gradient problem!
input layer
e(t)
h(t-1)
h(t)
h(t+1)
h(t+2)
h(t+3)
h(t+4)
y(t)
y(t+1)
y(t+2)
y(t+4)
y(t+3)
y(t+5)
Why
Why
Why
Why
Why
Whh
Whh
Whh
Whh
Whh
Wxh
Why
e(t+1)
e(t+2)
e(t+3)
e(t+4)
e(t+5)
vanishing gradient problem is exacerbated by having the same set of weights.
The vanishing gradient problem causes early layer to not to learn as effectively
The earlier layers learn from the remote past
As a result: vanilla RNN would only have short term memory (only learn from recent states)
Whh
Whh
Whh
Whh
Whh

MLTSA:
LSTM
4


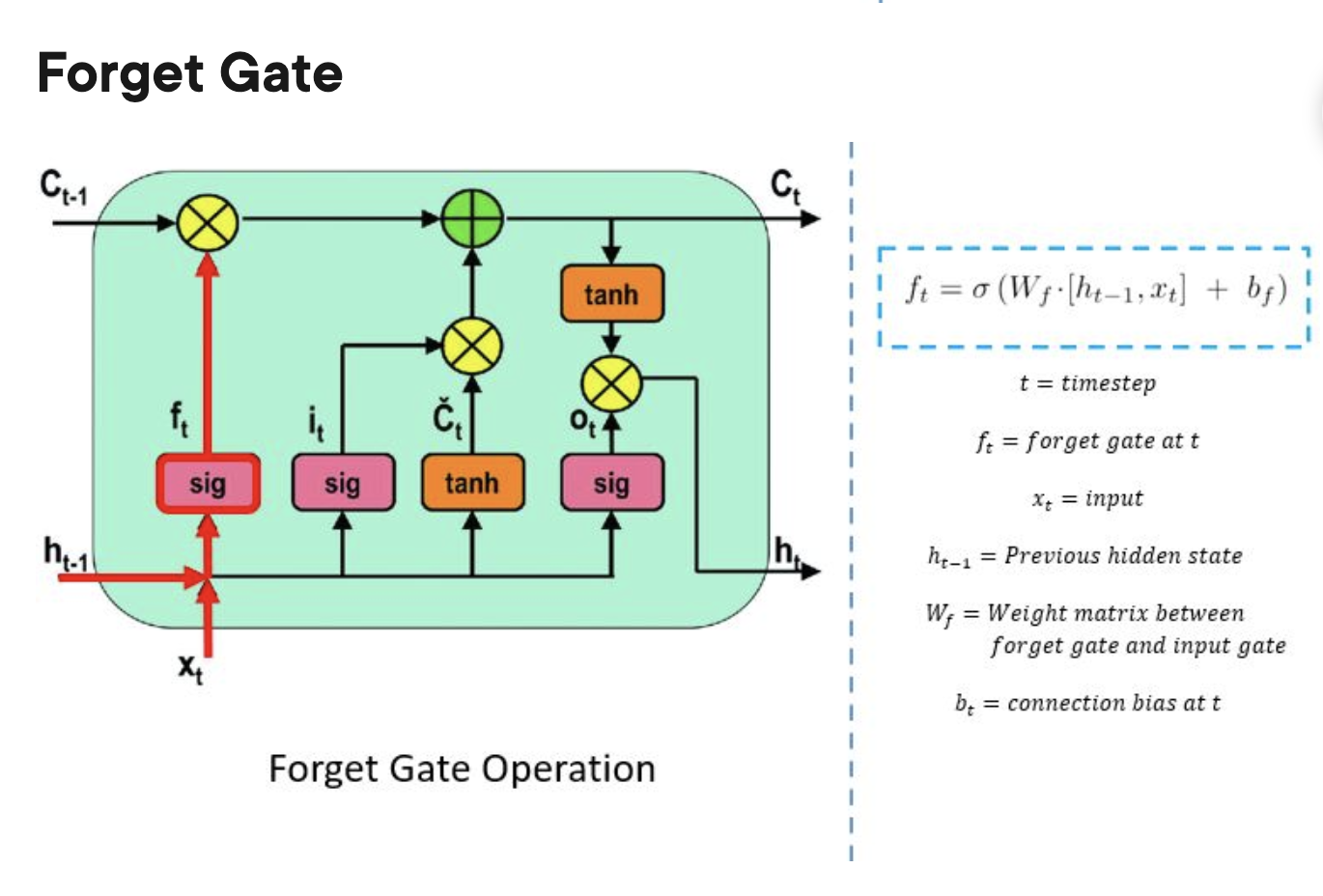
Ct: output
h: hidden states
X: input
Ct-1 : previous cell state (previous output)
ht-1 : previous hidden state
xt : current state (input)
forget gate:
do i keep memory of this past step
LSTM: long short term memory
solution to the vanishing gradient problem
input gate:
do I update the current cell?

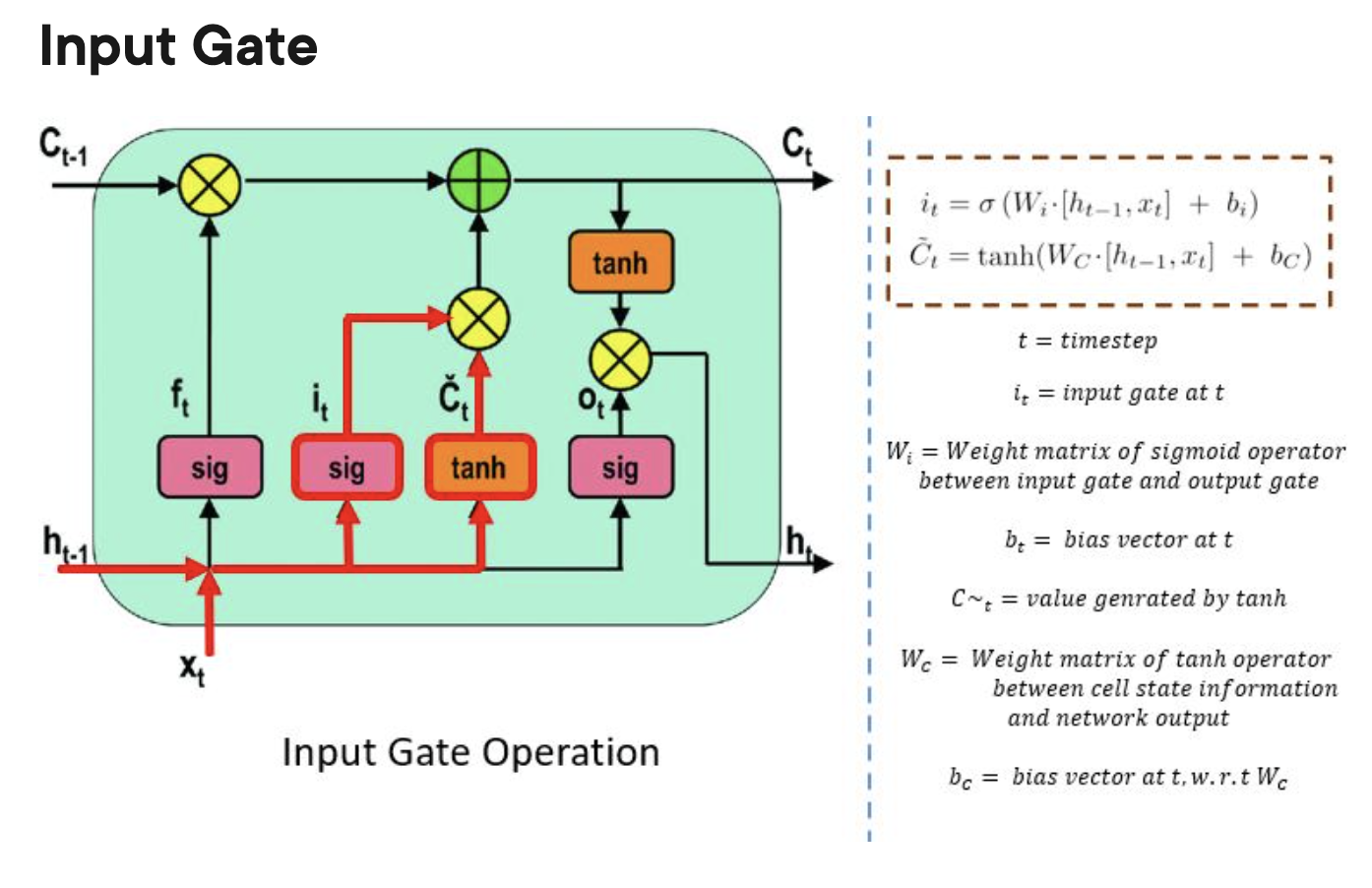
LSTM: long short term memory
solution to the vanishing gradient problem
cell state:
procuces the prediction
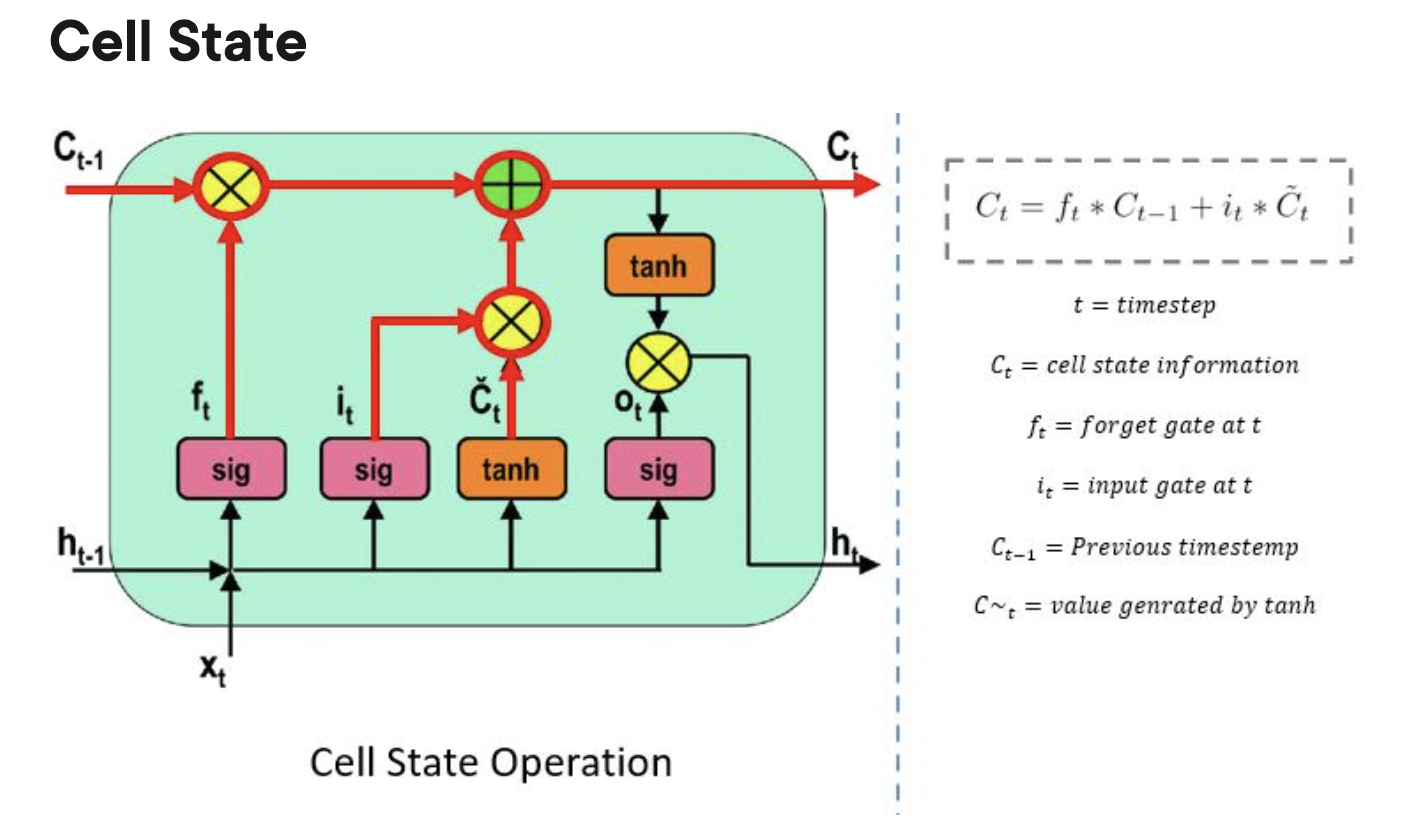

LSTM: long short term memory
solution to the vanishing gradient problem
output gate
previous input that goes into the hidden state

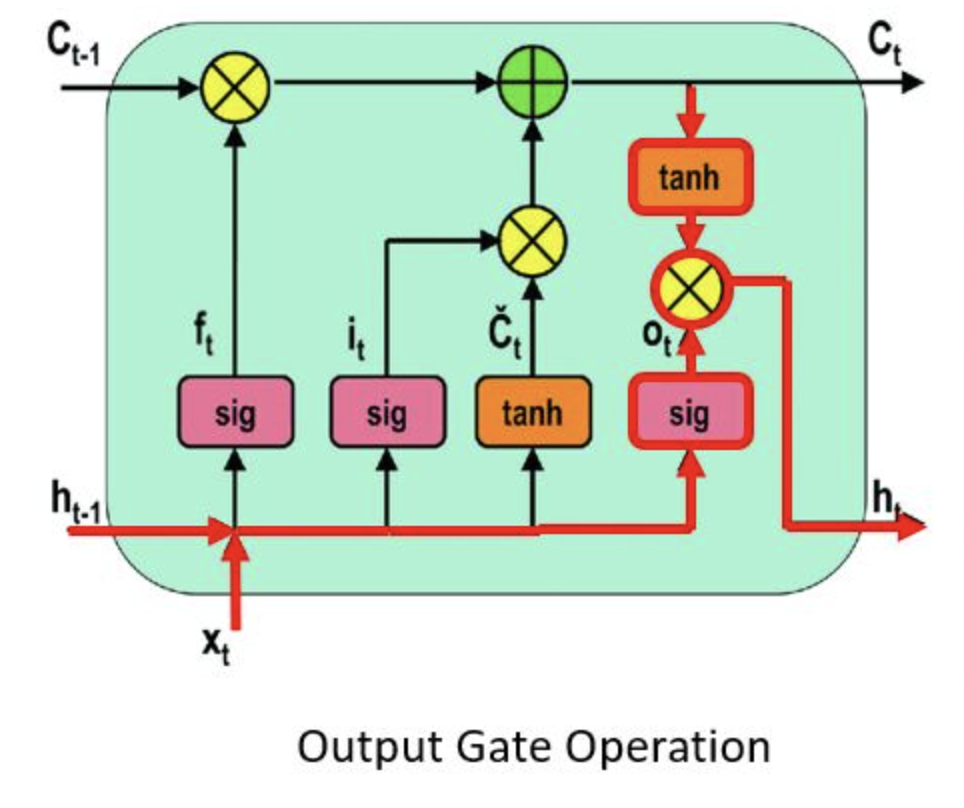

LSTM: long short term memory
solution to the vanishing gradient problem
hidden state
produces the new hidden states


LSTM: long short term memory
solution to the vanishing gradient problem
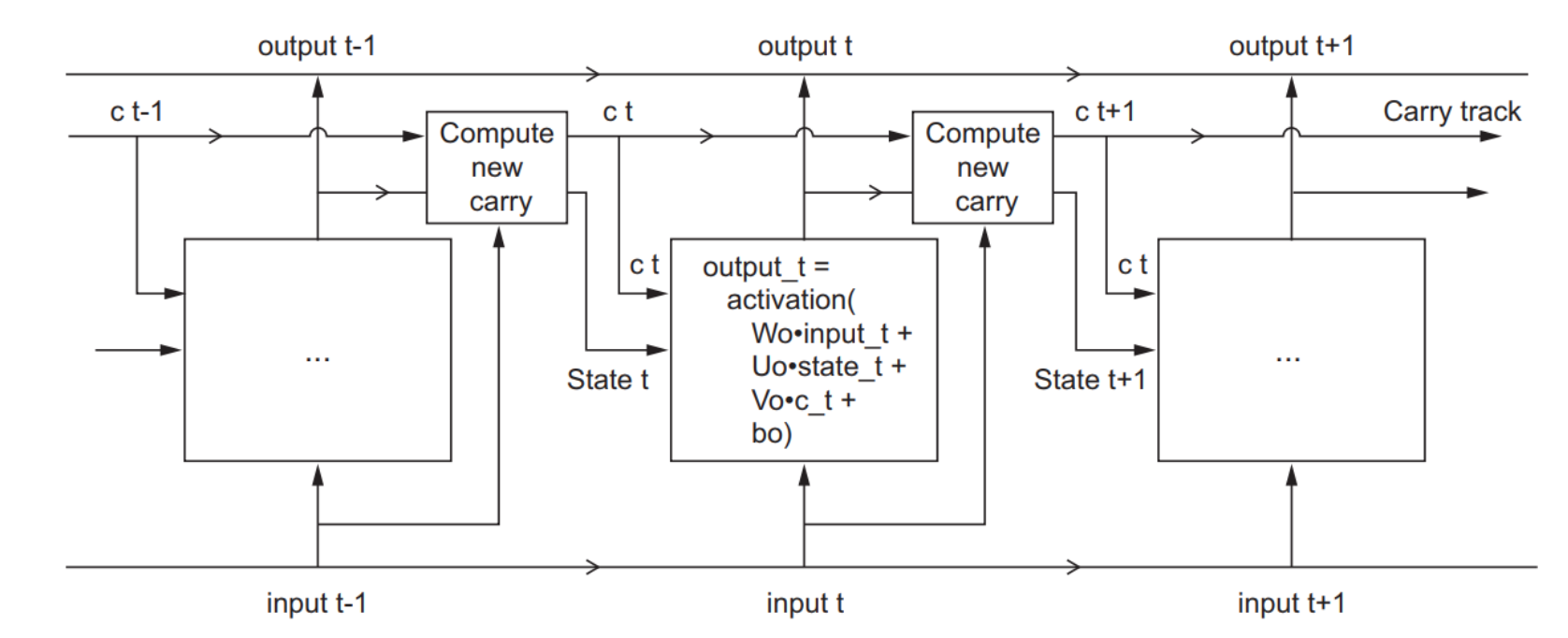
LSTM: long short term memory
solution to the vanishing gradient problem
even if you want to predict a single time series, you need many example
split the time series into chunks
LSTM: how to actually run it
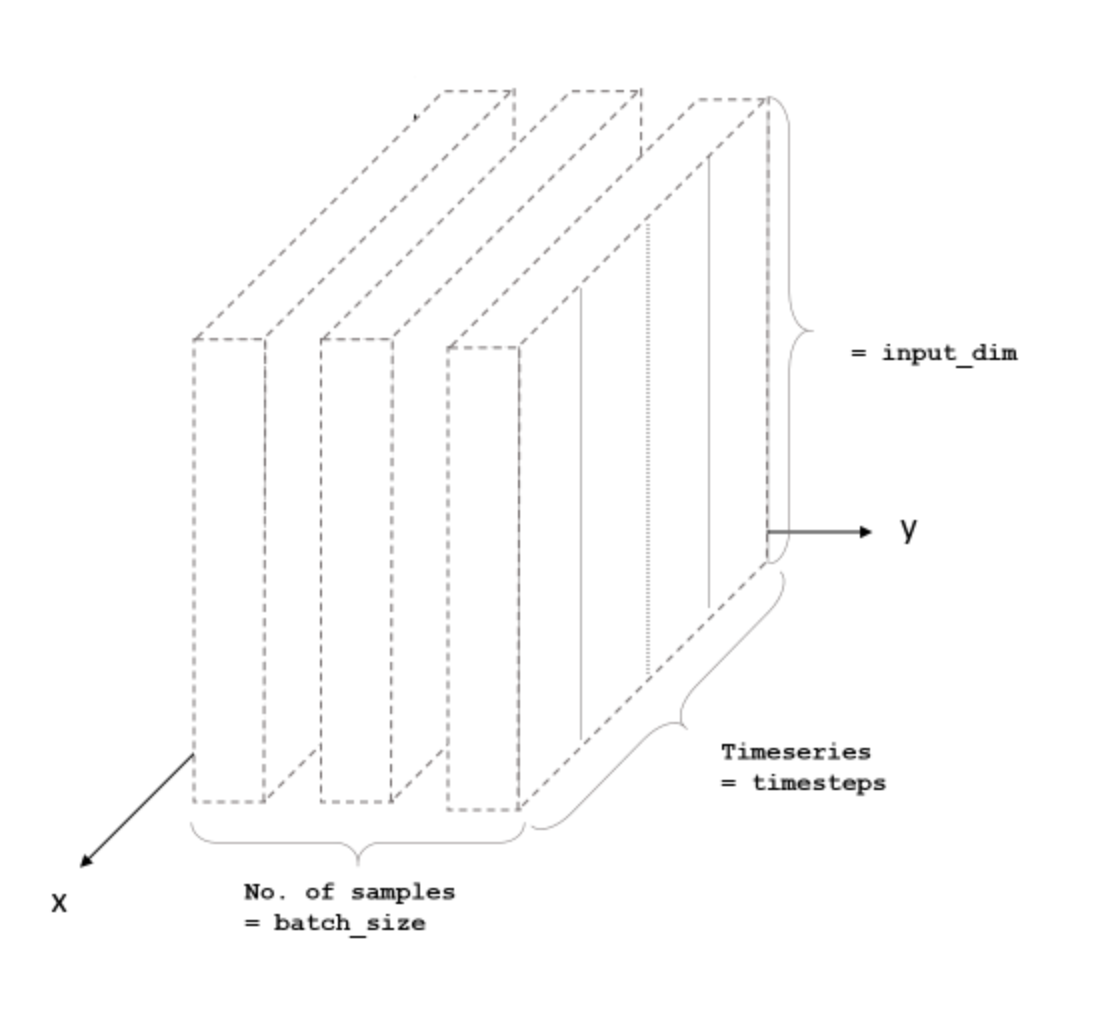
batch size: how many sequencies you pass at once
timeseries: how many time stamps in a sequence
features: how many measurements in the time seris
even if you want to predict a single time series, you need many example
split the time series into chunks
LSTM: how to actually run it


batch size: N
timeseries: 1000
features: 2
model = Sequential()
model.add(LSTM(32, input_shape=(50, 2)))
model.add(Dense(2))even if you want to predict a single time series, you need many example
split the time series into chunks
LSTM: how to actually run it

To be or not to be? this is the question. Whether 'tis nobler in the mind
sequencies of 12 letters
batch size: N
timeseries: 12
features: 1
LSTM: how to actually run it
There is no homework on this cause I am at the end of the semester, but if you want to learn more I will upload an exercise over the weekend where you will train an RNN to generate physics paper titles!


MLTSA:
visualizing NNs
5

Saliency Maps
Visualizing the predictions and the “neuron” firings in the RNN https://sungsoo.github.io/2017/01/08/recurrent-neural-networks.html
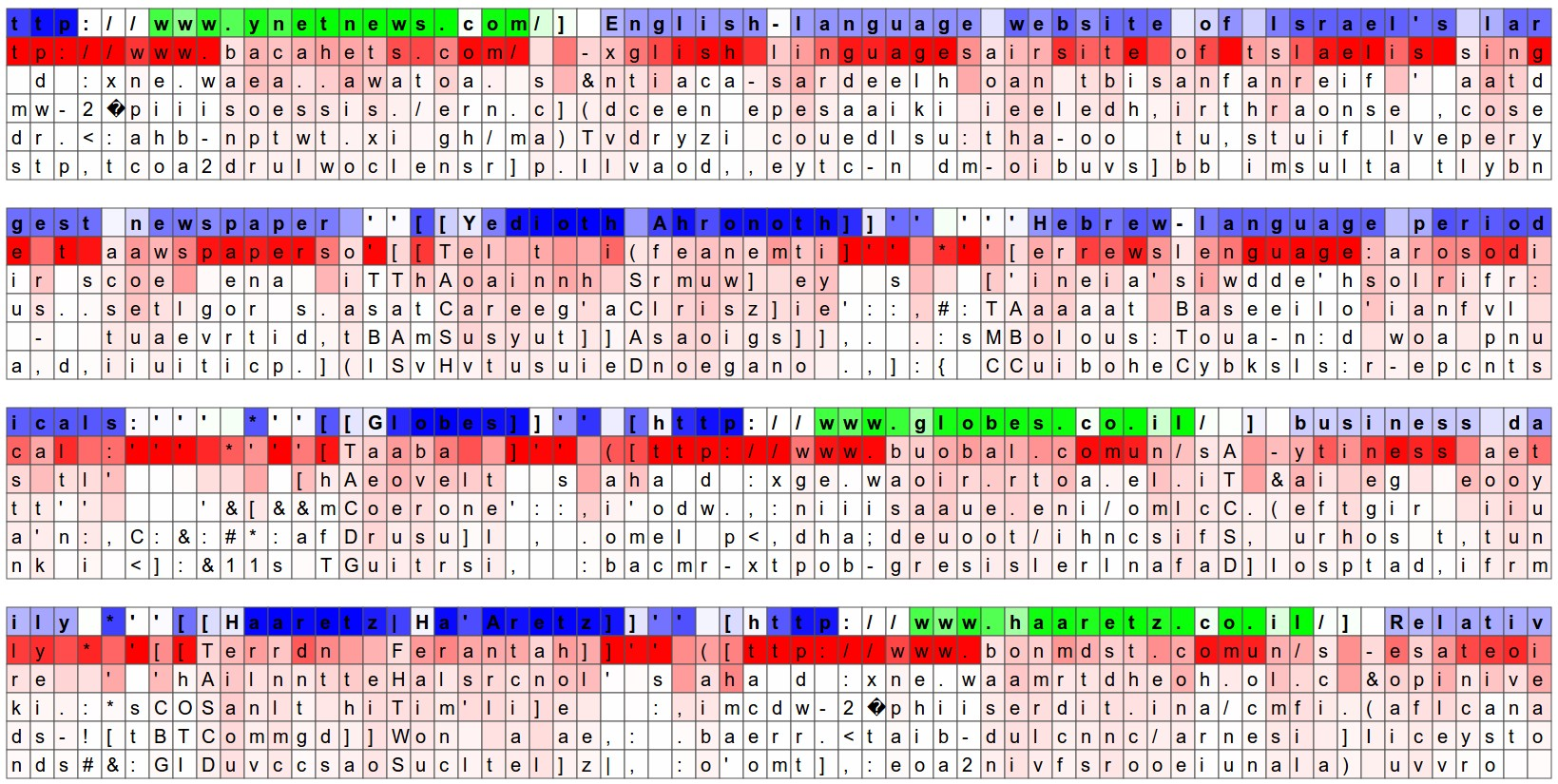
Visualizing the predictions and the “neuron” firings in the RNN https://sungsoo.github.io/2017/01/08/recurrent-neural-networks.html

"The guesses are colored by their probability (so dark red = judged as very likely, white = not very likely).
...
The input character sequence (blue/green) is colored based on the firing of a randomly chosen neuron in the hidden representation of the RNN. Think about it as green = very excited and blue = not very excited (... these are values between [-1,1] in the hidden state vector, which is just the gated and tanh’d LSTM cell state).
Intuitively, this is visualizing the firing rate of some neuron in the “brain” of the RNN while it reads the input sequence. Different neurons might be looking for different patterns.
learning markdown syntax: URL's
Visualizing the predictions and the “neuron” firings in the RNN https://sungsoo.github.io/2017/01/08/recurrent-neural-networks.html
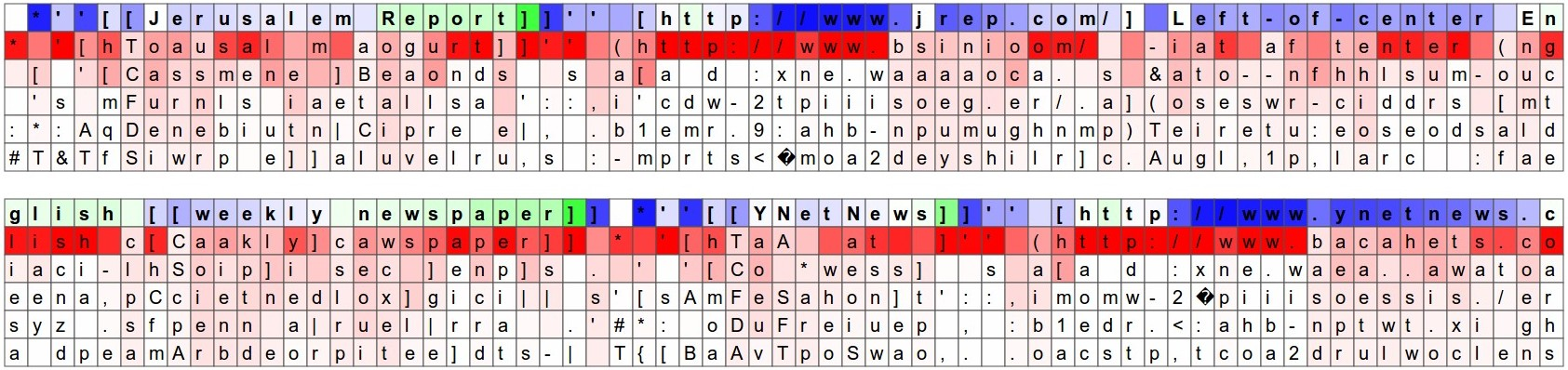
learning markdown syntax: [[]]
"The guesses are colored by their probability (so dark red = judged as very likely, white = not very likely).
...
The input character sequence (blue/green) is colored based on the firing of a randomly chosen neuron in the hidden representation of the RNN. Think about it as green = very excited and blue = not very excited (... these are values between [-1,1] in the hidden state vector, which is just the gated and tanh’d LSTM cell state).
Intuitively, this is visualizing the firing rate of some neuron in the “brain” of the RNN while it reads the input sequence. Different neurons might be looking for different patterns.
Visualizing the predictions and the “neuron” firings in the RNN
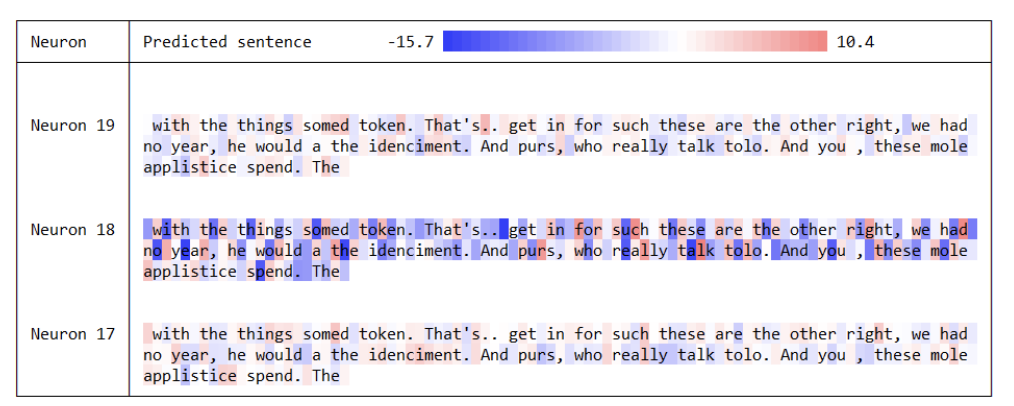
Vanilla RNN
Visualizing the predictions and the “neuron” firings in the RNN
LSTM


reading
The Unreasonable Effectiveness of Recurrent Neural Networks
andrej karpathy
http://karpathy.github.io/2015/05/21/rnn-effectiveness/
not mandatory
resources
Neural Network and Deep Learning
an excellent and free book on NN and DL
http://neuralnetworksanddeeplearning.com/index.html
Deep Learning An MIT Press book in preparation
Ian Goodfellow, Yoshua Bengio and Aaron Courville
https://www.deeplearningbook.org/lecture_slides.html
History of NN
https://cs.stanford.edu/people/eroberts/courses/soco/projects/neural-networks/History/history2.html