Neural Networks 101
Opportunity

the era of AI
experiment driven science -∞:1900
theory driven science 1900-1950
data driven science 1990-2010
the fourth paradigm - Jim Gray, 2009
computationally driven science 1950-1990
experiment driven science -∞:1900
theory driven science 1900-1950
data driven science 1990-2010
the fourth paradigm - Jim Gray, 2009
computationally driven science 1950-1990
AI driven science? 2010...
Input
x
y
output
Input
x
y
output
function
Input
x
y
output
b
m
m: slope
b: intercept
Input
x
y
output
b
m
m: slope
b: intercept
parameters
Input
x
y
output
b
m
m: slope
b: intercept
parameters
x
y
goal: find the right m and b that turn x into y
goal: find the right m and b that turn x into y
Input
x
y
output
b
m
m: slope
b: intercept
parameters
x
y
learn
goal: find the right m and b that turn x into y
goal: find the right m and b that turn x into y
what is machine learning?
1
what is machine learning?
ML: any model with parameters learnt from the data
Input
x
y
output
m = 0.4 and b=0
m: slope
b: intercept
parameters
x
let's try
goal: learn the right m and b that turn x into y
m
L2
-1.4
-.5
.6
1.5
2.4
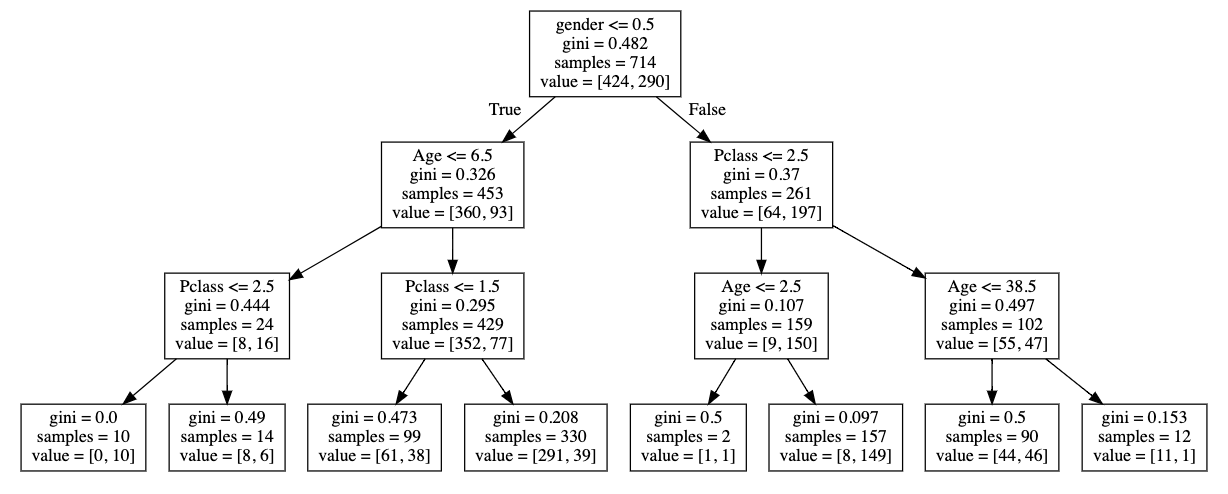
Tree models
(at the basis of Random Forest
Gradient Boosted Trees)
Machine Learning


p(class)
extracted
features vector

p(class)
pixel values tensor
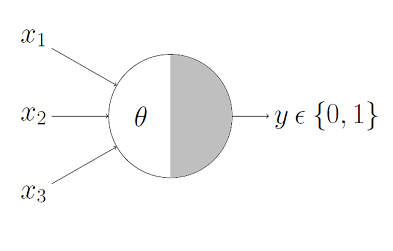
w1
w1
w2
w2
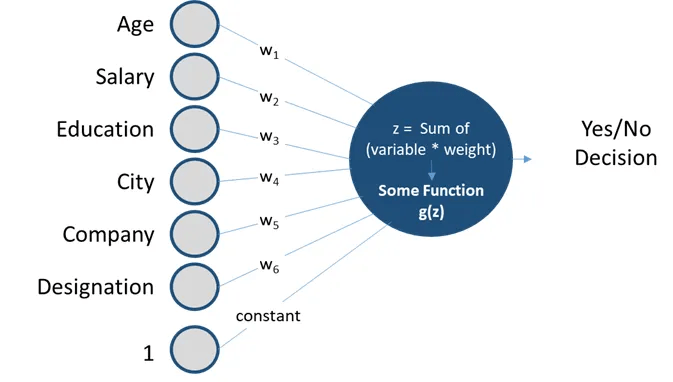
The perceptron algorithm : 1958, Frank Rosenblatt
1958
Perceptron
The perceptron algorithm : 1958, Frank Rosenblatt
.
.
.
output
weights
bias
linear regression:
1958
Perceptron
.
.
.
output
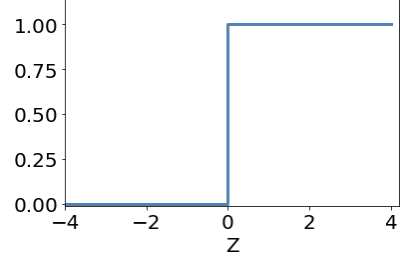
activation function
weights
bias
The perceptron algorithm : 1958, Frank Rosenblatt
Perceptrons are linear classifiers: makes its predictions based on a linear predictor function
combining a set of weights (=parameters) with the feature vector.
Perceptron
The perceptron algorithm : 1958, Frank Rosenblatt
output
activation function
weights
bias
sigmoid
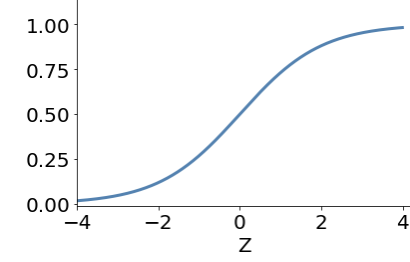
.
.
.
Perceptrons are linear classifiers: makes its predictions based on a linear predictor function
combining a set of weights (=parameters) with the feature vector.
Perceptron
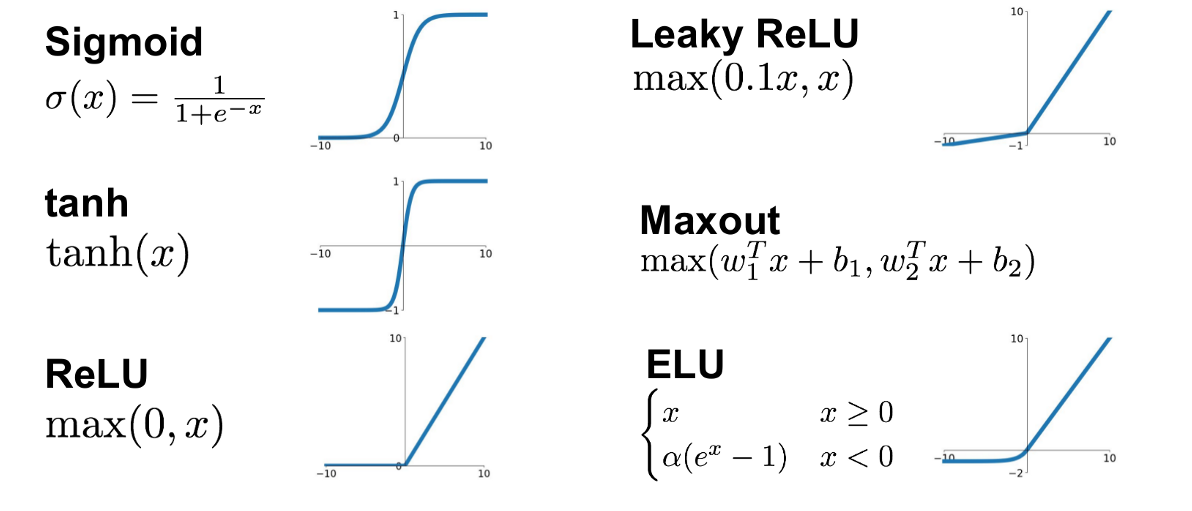
ANN examples of activation function
The perceptron algorithm : 1958, Frank Rosenblatt
Perceptron

The Navy revealed the embryo of an electronic computer today that it expects will be able to walk, talk, see, write, reproduce itself and be conscious of its existence.
The embryo - the Weather Buerau's $2,000,000 "704" computer - learned to differentiate between left and right after 50 attempts in the Navy demonstration
NEW NAVY DEVICE LEARNS BY DOING; Psychologist Shows Embryo of Computer Designed to Read and Grow Wiser
July 8, 1958

Input
x
y
output
x
y
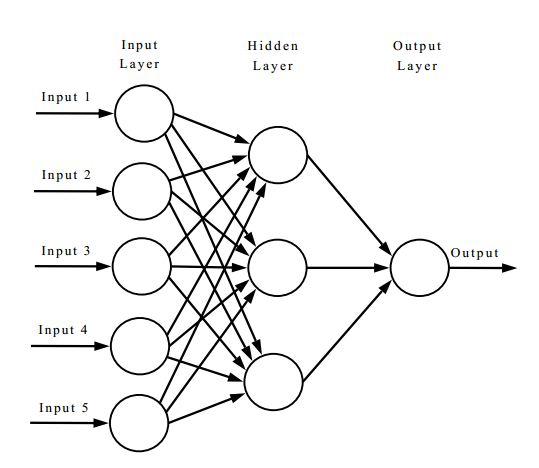
A Neural Network is a kind of function that maps input to output
multilayer perceptron
output
layer of perceptrons
multilayer perceptron
output
input layer
hidden layer
output layer
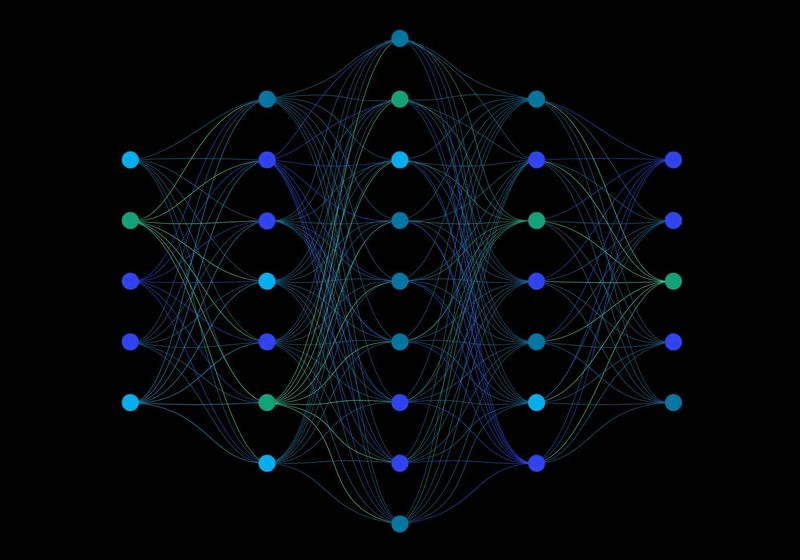
1970: multilayer perceptron architecture
Fully connected: all nodes go to all nodes of the next layer.
Perceptrons by Marvin Minsky and Seymour Papert 1969
multilayer perceptron
output
layer of perceptrons
multilayer perceptron
output
layer of perceptrons
multilayer perceptron
layer of perceptrons
output
layer of perceptrons
multilayer perceptron
output
Fully connected: all nodes go to all nodes of the next layer.
layer of perceptrons
multilayer perceptron
output
Fully connected: all nodes go to all nodes of the next layer.
layer of perceptrons
w: weight
sets the sensitivity of a neuron
b: bias:
up-down weights a neuron
learned parameters
multilayer perceptron
output
Fully connected: all nodes go to all nodes of the next layer.
layer of perceptrons
w: weight
sets the sensitivity of a neuron
b: bias:
up-down weights a neuron
f: activation function:
turns neurons on-off
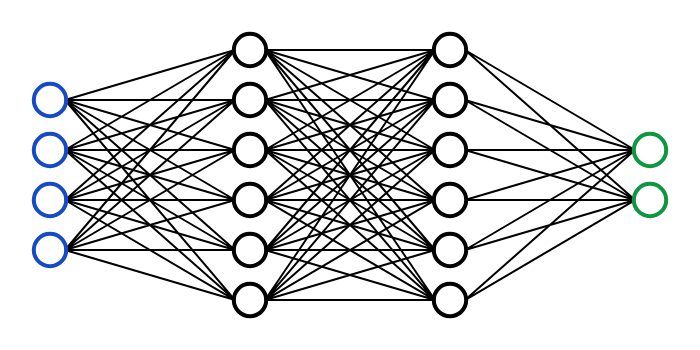
DNN:
hyperparameters of DNN
3
EXERCISE
output
how many parameters?
input layer
hidden layer
output layer
hidden layer
EXERCISE
output
how many parameters?
input layer
hidden layer
output layer
hidden layer
output
input layer
hidden layer
output layer
hidden layer
35
(3x4)+4
(4x3)+3
how many parameters?
EXERCISE
(3)+1
output
input layer
hidden layer
output layer
hidden layer
- number of layers- 1
- number of neurons/layer-
- activation function/layer-
- layer connectivity-
- optimization metric - 1
- optimization method - 1
- parameters in optimization- M
how many hyperparameters?
EXERCISE
GREEN: architecture hyperparameters
RED: training hyperparameters
EXERCISE
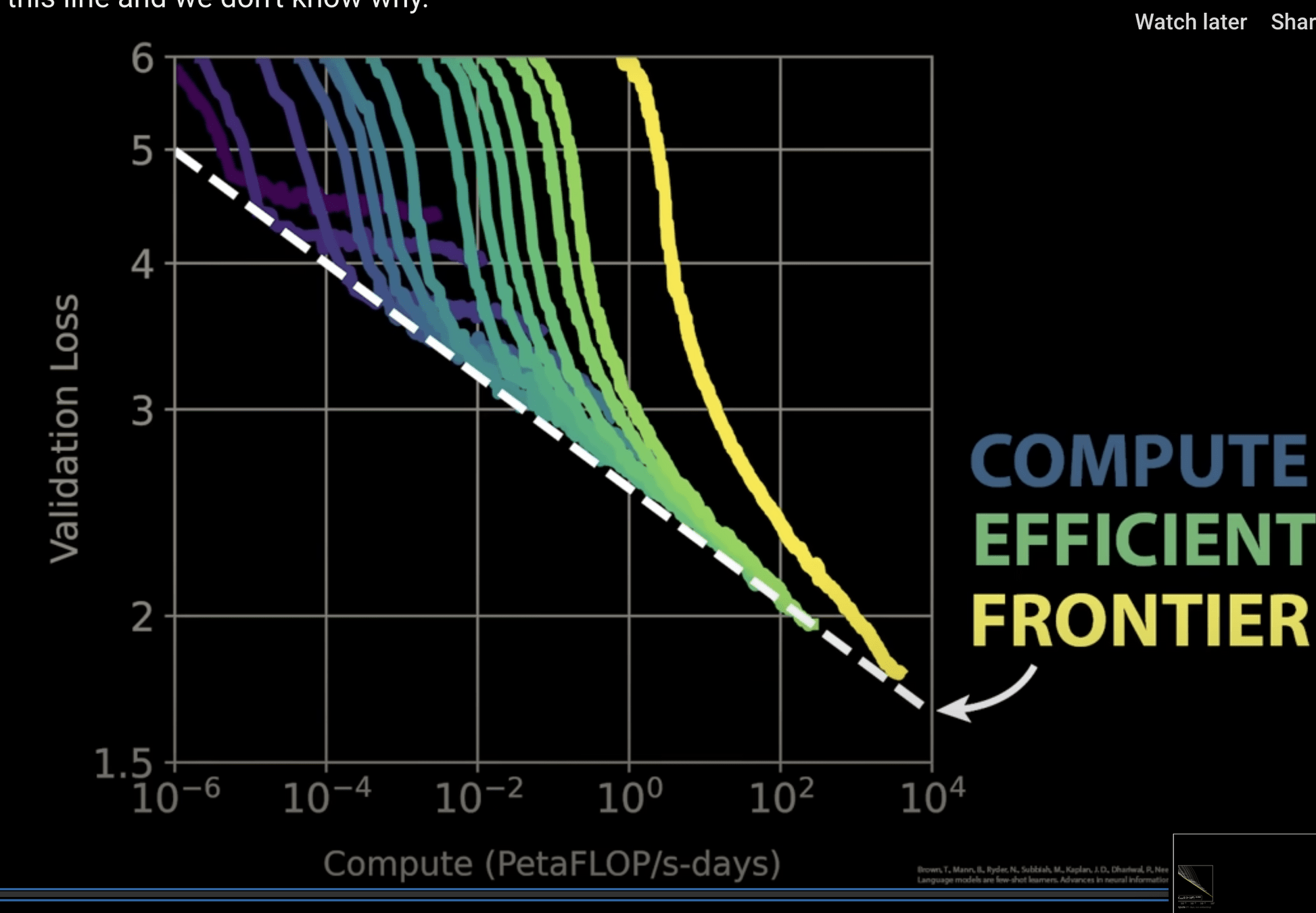
GPT-3
175 Billion Parameters
3,640 PetaFLOPs days
Kaplan+ 2020
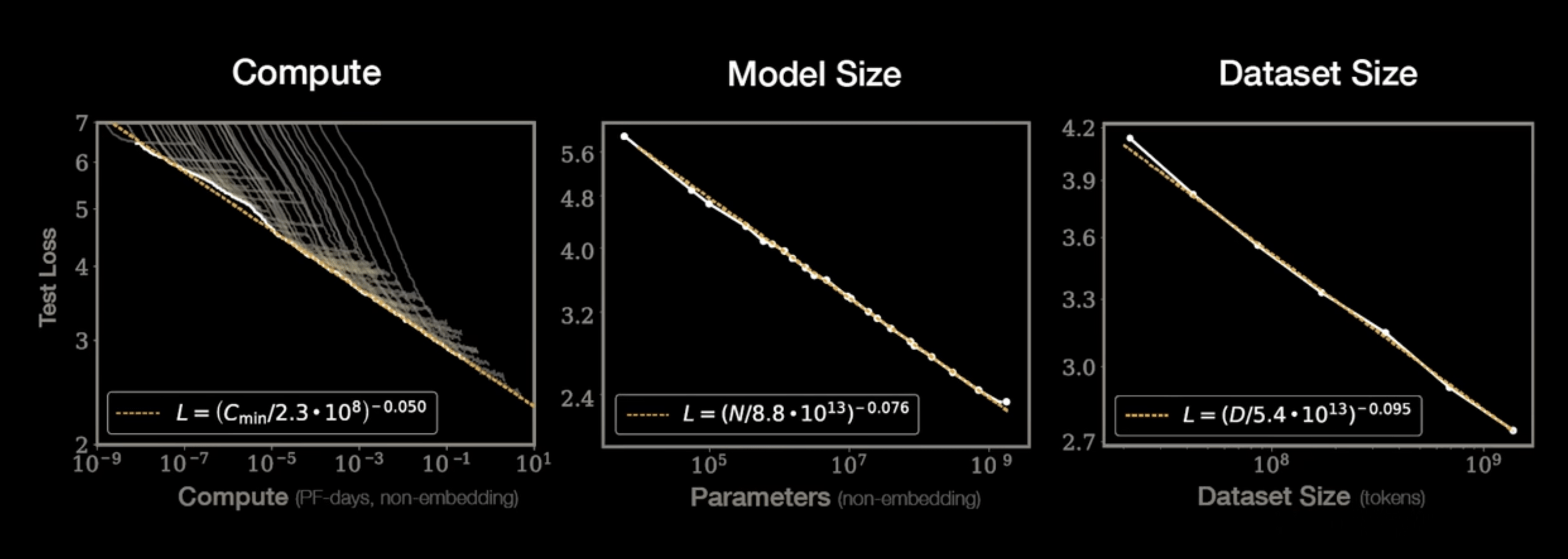
Kaplan+ 2020
x
y
A Neural Network is a kind of function that maps input to output
Input
output
hidden layers
latent space
x
y
A Neural Network is a kind of function that maps input to output

Input
output
hidden layers
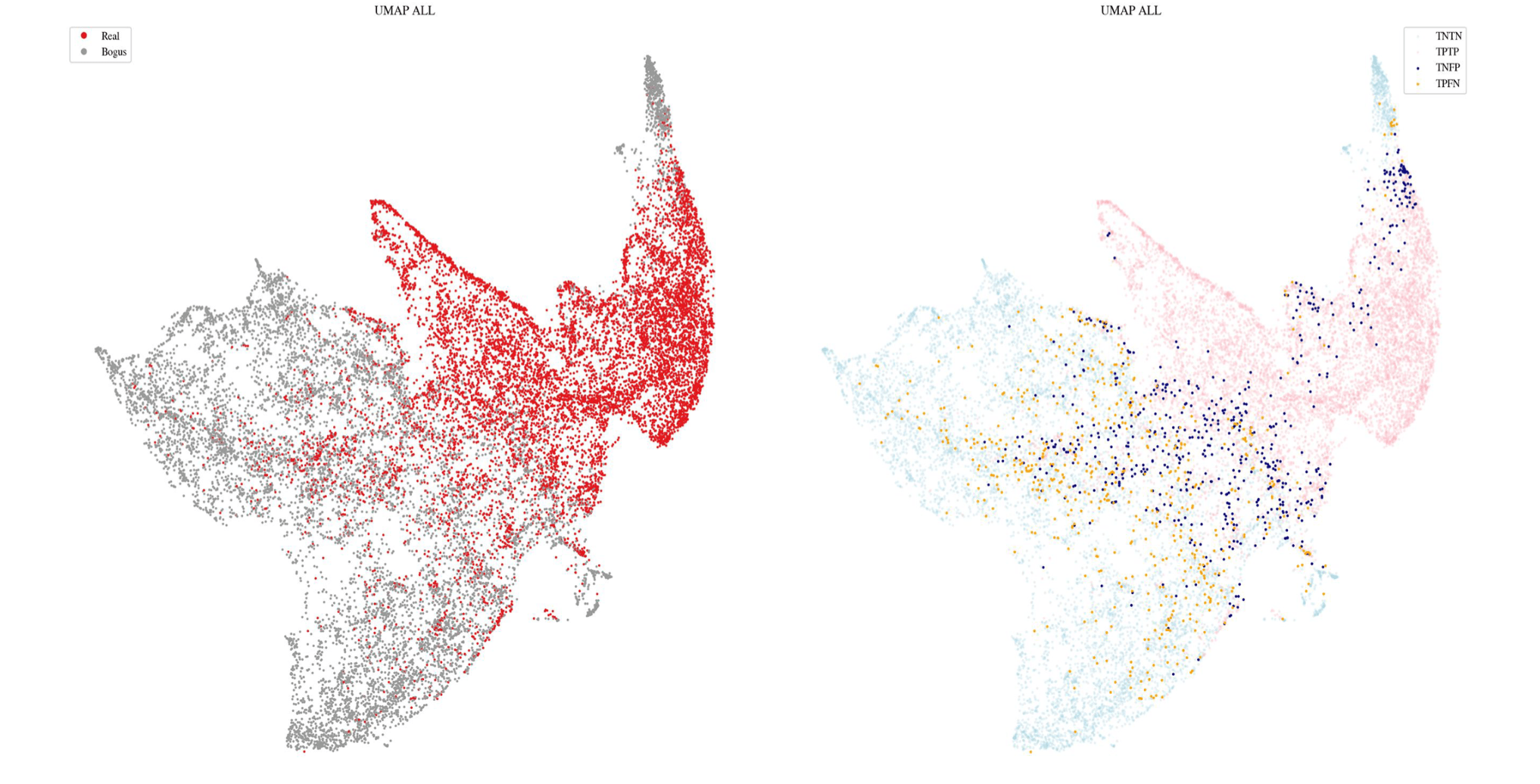
latent space


visualizatoin and concept credit: Alex Razim
Kaicheng Zhang et al 2016 ApJ 820 67
deSoto+2024
Boone 2017
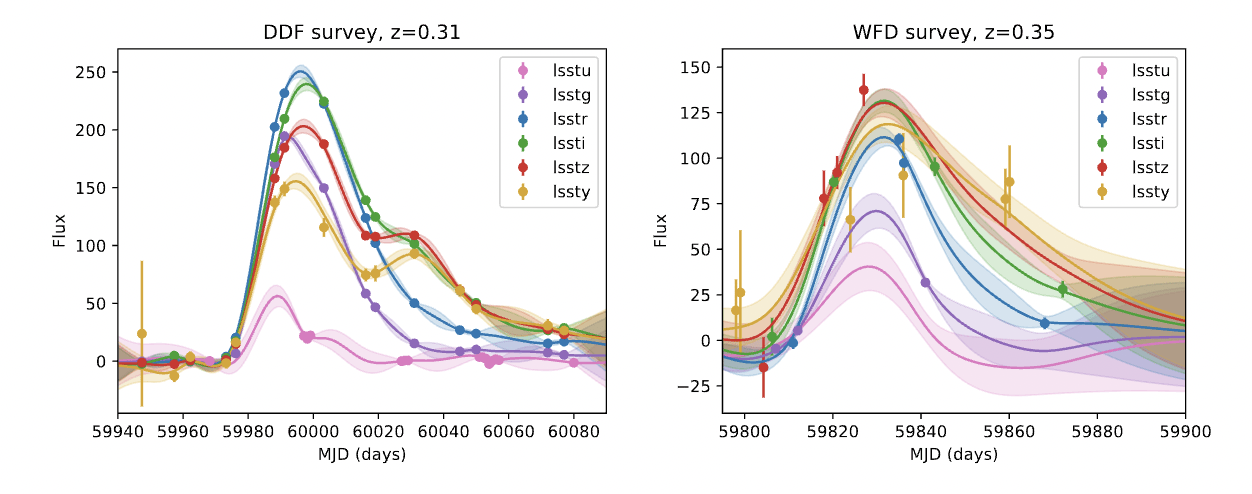

7% of LSST data
The rest
















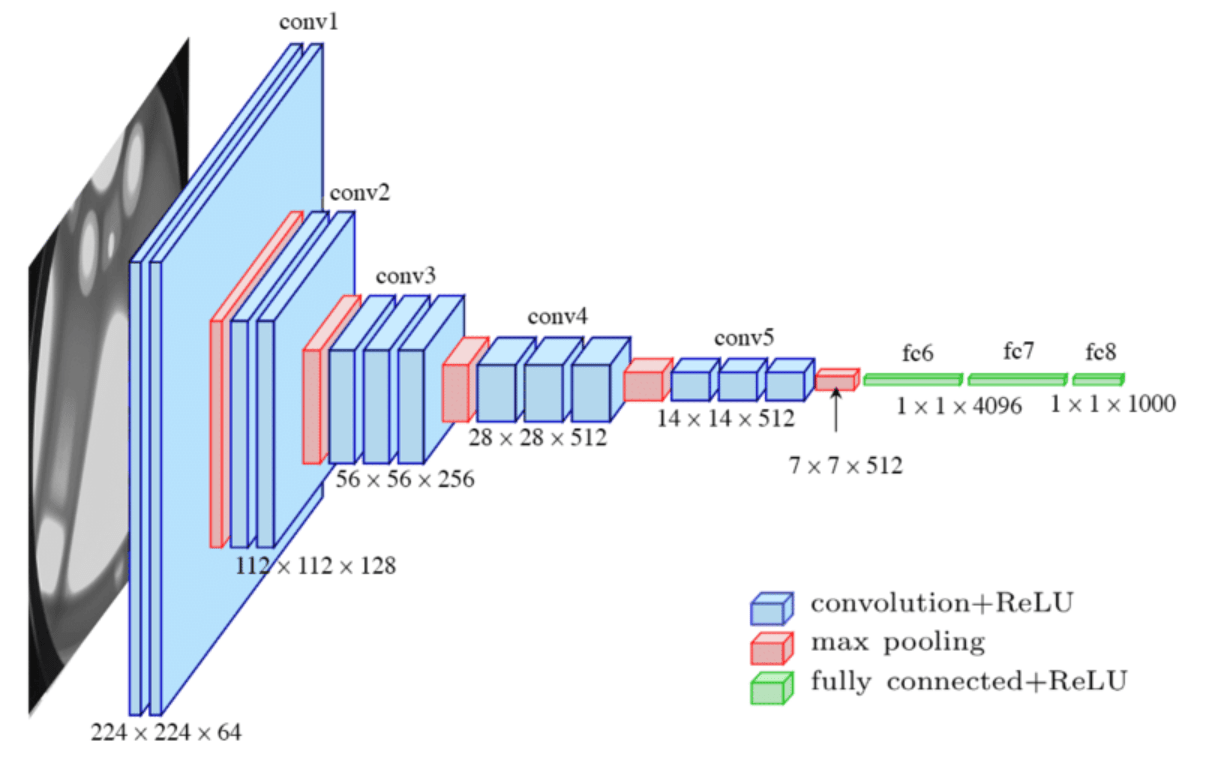
late layers learn complex aggregate specialized features


early layers learn simple generalized features (like lines for CNN)
prediction "head"
original data

trained extensively on large amounts of data to solve generic problems
Foundational AI models
trained extensively on large amounts of data to solve generic problems
Foundational AI models

We use the ILSVRC-2012 ImageNet dataset with 1k classes
and 1.3M images, its superset ImageNet-21k with
21k classes and 14M images and JFT with 18k classes and
303M high-resolution images.
Typically, we pre-train ViT on large datasets, and fine-tune to (smaller) downstream tasks. For
this, we remove the pre-trained prediction head and attach a zero-initialized D × K feedforward
layer, where K is the number of downstream classe
trained extensively on large amounts of data to solve generic problems
Foundational AI models


We use the ILSVRC-2012 ImageNet dataset with 1k classes
and 1.3M images, its superset ImageNet-21k with
21k classes and 14M images and JFT with 18k classes and
303M high-resolution images.
Typically, we pre-train ViT on large datasets, and fine-tune to (smaller) downstream tasks. For
this, we remove the pre-trained prediction head and attach a zero-initialized D × K feedforward
layer, where K is the number of downstream classe

Lots of parameters and lots of hyperparameters! What to choose?
cheatsheet
-
architecture - wide networks tend to overfit, deep networks are hard to train
- number of epochs - the sweet spot is when learning slows down, but before you start overfitting... it may take DAYS! jumps may indicate bad initial choices (like in all gradient descent)
- loss function - needs to be appropriate to the task, e.g. classification vs regression
-
activation functions - needs to be consistent with the loss function
- optimization scheme - needs to be appropriate to the task and data
- learning rate in optimization - balance speed and accuracy
- batch size - smaller batch size is faster but leads to overtraining
An article that compars various DNNs

An article that compars various DNNs

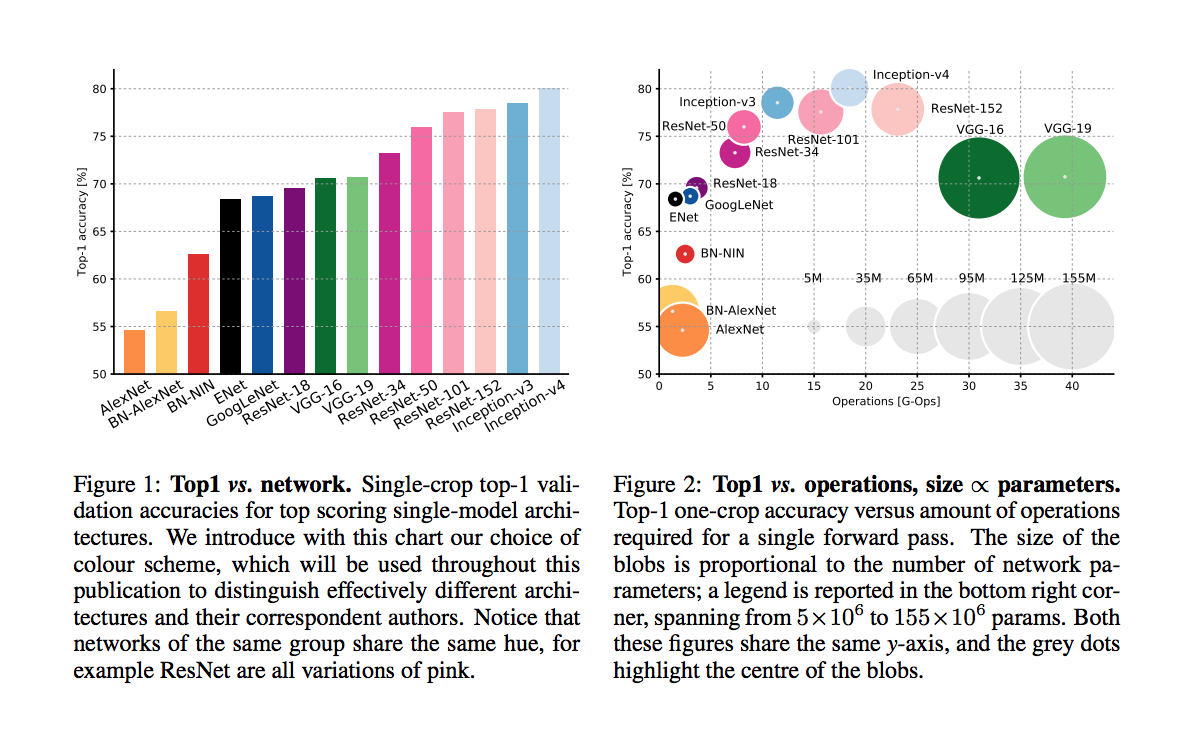
accuracy comparison
An article that compars various DNNs

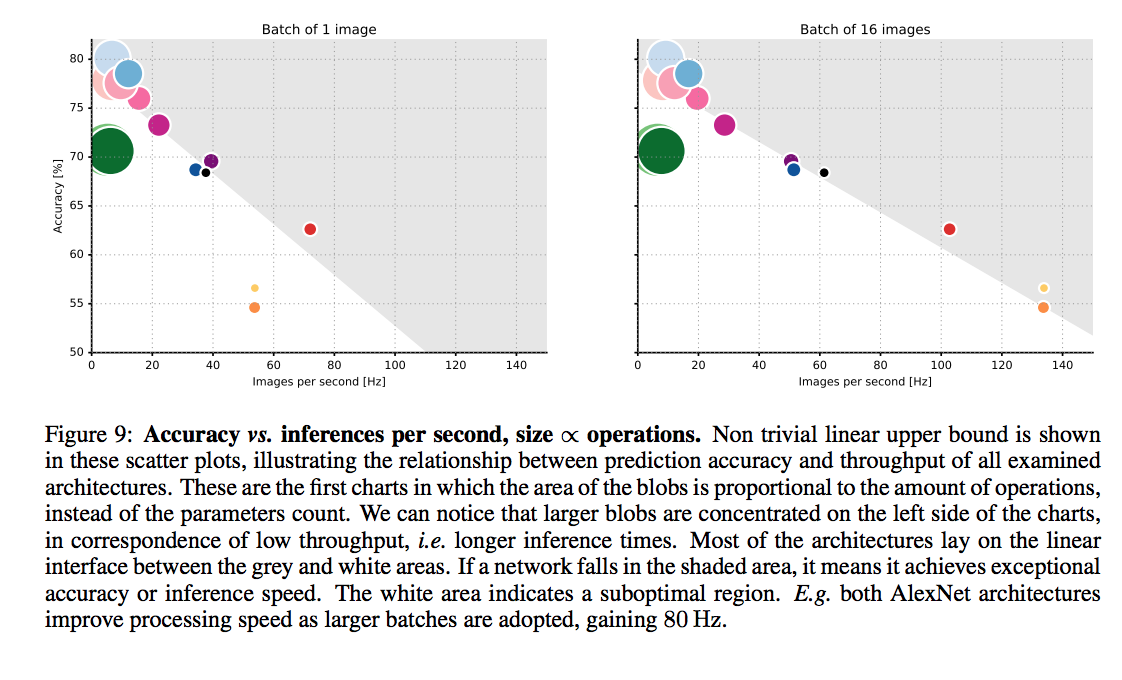
batch size

Lots of parameters and lots of hyperparameters! What to choose?
cheatsheet
- architecture - wide networks tend to overfit, deep networks are hard to train
-
number of epochs - the sweet spot is when learning slows down, but before you start overfitting... it may take DAYS! jumps may indicate bad initial choices
-
loss function - needs to be appropriate to the task, e.g. classification vs regression
-
activation functions - needs to be consistent with the loss function
- optimization scheme - needs to be appropriate to the task and data
- learning rate in optimization - balance speed and accuracy
- batch size - smaller batch size is faster but leads to overtraining


What should I choose for the loss function and how does that relate to the activation functiom and optimization?
Lots of parameters and lots of hyperparameters! What to choose?

Lots of parameters and lots of hyperparameters! What to choose?
cheatsheet
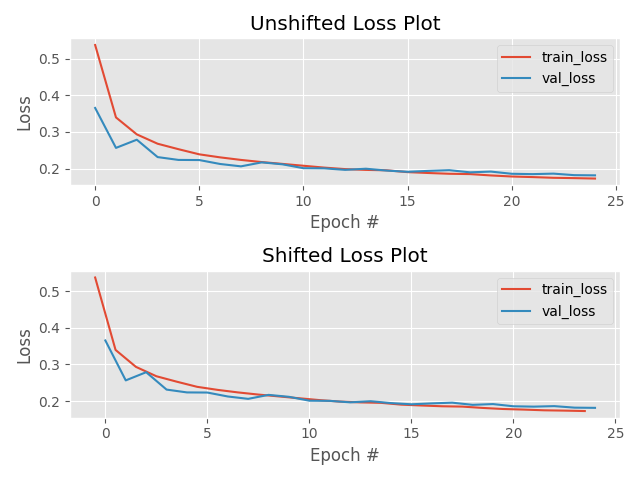
always check your loss function! it should go down smoothly and flatten out at the end of the training.
not flat? you are still learning!
too flat? you are overfitting...
loss (gallery of horrors)
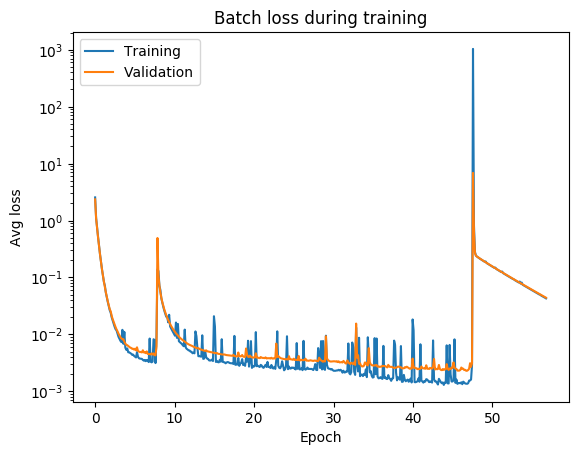
jumps are not unlikely (and not necessarily a problem) if your activations are discontinuous (e.g. relu)
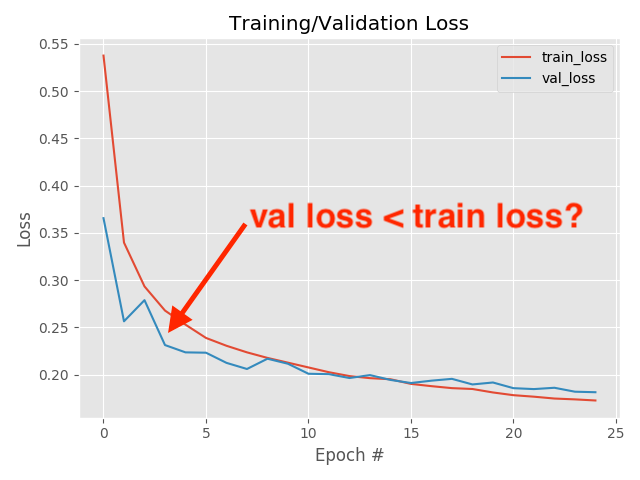
when you use validation you are introducing regularizations (e.g. dropout) so the loss can be smaller than for the training set
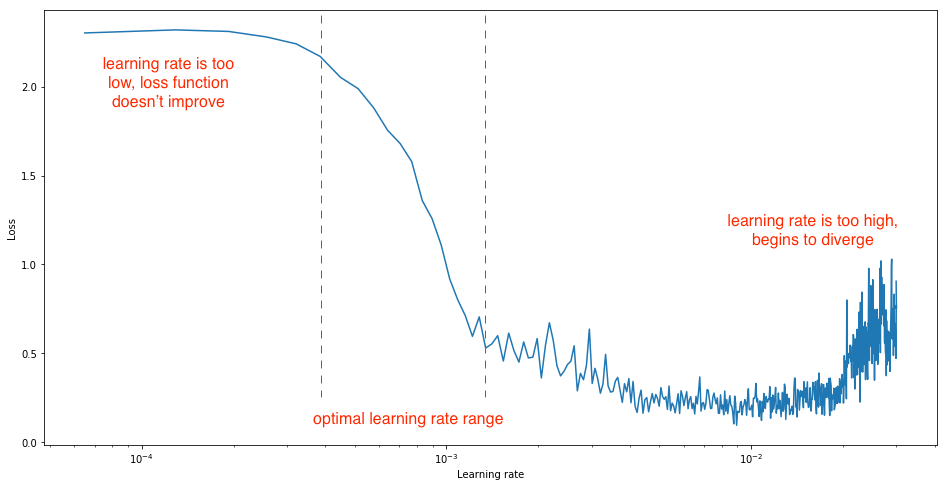
loss and learning rate (not that the appropriate learning rate depends on the chosen optimization scheme!)

Building a DNN
with keras and tensorflow
autoencoder for image recontstruction
What should I choose for the loss function and how does that relate to the activation functiom and optimization?
| loss | good for | activation last layer | size last layer |
|---|---|---|---|
| mean_squared_error | regression | linear | one node |
| mean_absolute_error | regression | linear | one node |
| mean_squared_logarithmit_error | regression | linear | one node |
| binary_crossentropy | binary classification | sigmoid | one node |
| categorical_crossentropy | multiclass classification | sigmoid | N nodes |
| Kullback_Divergence | multiclass classification, probabilistic inerpretation | sigmoid | N nodes |
On the interpretability of DNNs
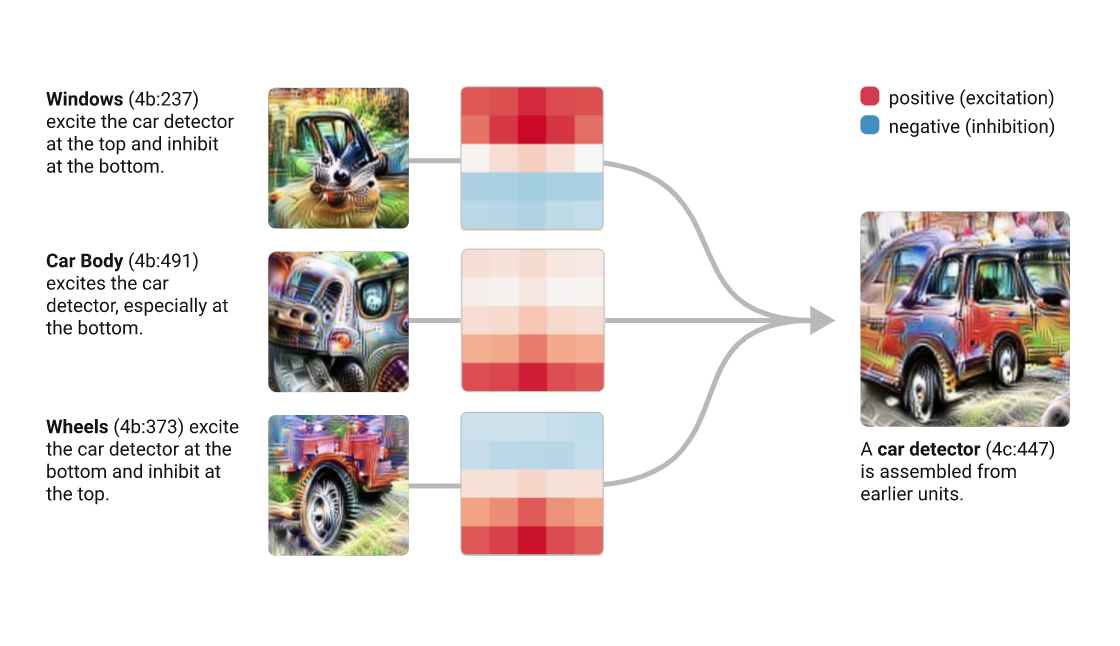


resources
Neural Network and Deep Learning
an excellent and free book on NN and DL
http://neuralnetworksanddeeplearning.com/index.html
History of NN
https://cs.stanford.edu/people/eroberts/courses/soco/projects/neural-networks/History/history2.html
NN are a vast topics and we only have 2 weeks!
Some FREE references!

michael nielsen
better pedagogical approach, more basic, more clear
ian goodfellow
mathematical approach, more advanced, unfinished
michael nielsen
better pedagogical approach, more basic, more clear
An article that compars various DNNs


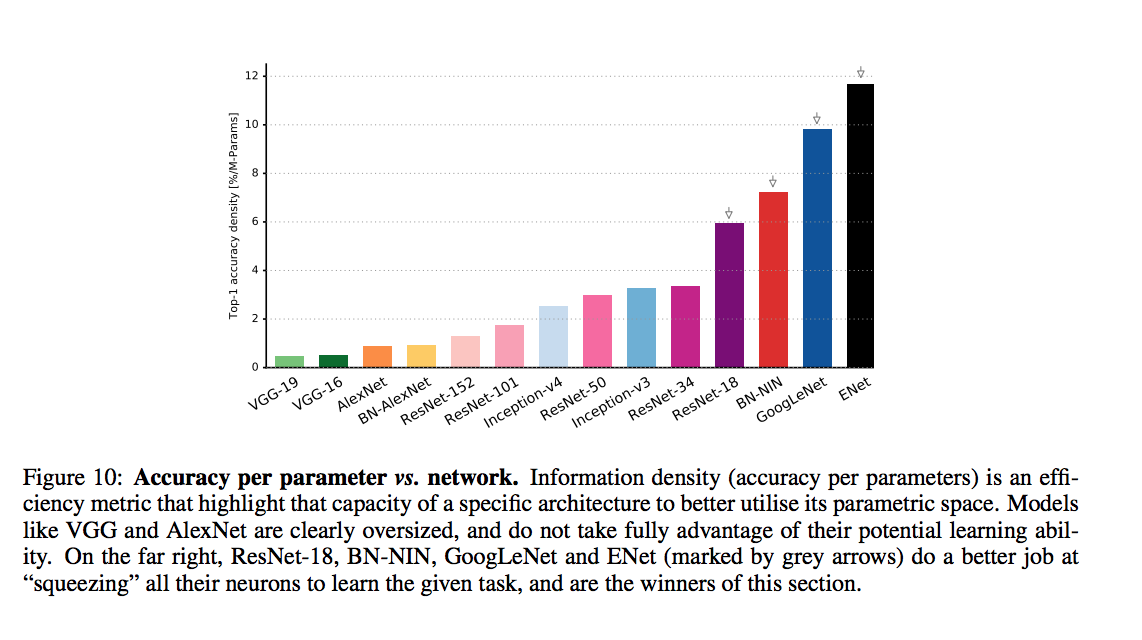
accuracy comparison