PHYS 207.013

Chapter 6

Friction and drag

Instructor: Dr. Bianco

TAs: Joey Betz; Lily Padlow

 

University of Delaware - Spring 2021

https://slides.com/federicabianco/phys20713_5

Friction 

H&R CH6 Friction

🚶🏻‍♀️

🚶🏾‍♂️

Friction is a force with an unusual behavior

H&R CH6 Friction

  • it does not have a constant value
  • there are different kinds of friction for moving and static objects
  • it is different for different materials

F = mg

Forces are balanced

 

 

no friction until anoter force is applied

\sum_i\vec{F}_i = m\vec{g} - \vec{N} = 0

F = N

H&R CH6 Friction

F = mg

F = N

Forces are balanced

 

 

 

\sum_i\vec{F}_i = m\vec{g} \cos{\theta}- \vec{N} = 0
\sum_i\vec{F}_i = m\vec{g} \sin{\theta}

H&R CH6 Friction

H&R CH6 Friction

F = mg

F = N

Forces are balanced

 

 

 

\sum_i\vec{F}_i = m\vec{g} \cos{\theta}- \vec{N} = 0
\sum_i\vec{F}_i = m\vec{g} \sin{\theta}

H&R CH6 Friction

F = mg

F = N

Forces are balanced

 

 

 

\sum_i\vec{F}_i = m\vec{g} \cos{\theta}- \vec{N} = 0
\sum_i\vec{F}_i = m\vec{g} \sin{\theta}

H&R CH6 Friction

Forces are balanced

 

 

 

\sum_i\vec{F}_i = m\vec{g} - \vec{N} = 0
\sum_i\vec{F}_i = \vec{F}- \vec{f}_s = 0
\sum_i\vec{F}_i = \vec{F}- \vec{f}_s = 0
\sum_i\vec{F}_i = \vec{F}- \vec{f}_{\mathrm{max},s} = 0
\sum_i\vec{F}_i = \vec{F}- \vec{f}_k > 0

increase the force

increase the force

H&R CH6 Friction

\sum_i\vec{F}_i = \vec{F}- \vec{f}_s = 0
\sum_i\vec{F}_i = \vec{F}- \vec{f}_s = 0
\sum_i\vec{F}_i = \vec{F}- \vec{f}_k > 0

}

H&R CH6 Friction

\sum_i\vec{F}_i = \vec{F}- \vec{f}_{\mathrm{max},s} = 0

KEY POINTS:

  • The force of friction between two surfeces that are not moving is larger than the force of friction between two bodies that are already moving (sliding) fk<fs   
  • fs is a force that acts between two body in contact against any force that tries to displace (slide) one of them
  • there is a maximum value for fs : fmax,s 

Force of riction

  • fs is not constant, grows with the force applies that tries to slide 

H&R CH6 Friction

H&R CH6 Friction

  • it does not have a constant value
  • there are different kinds of friction for moving and static objects
  • it is different for different materials

how it works at a microscopic level

how it works at a microscopic level

H&R CH6 Friction

"A frictional force is, in essence, the vector sum of many forces acting between the surface atoms of one body and those of another body.  "
 

how it works at a microscopic level

H&R CH6 Friction

"A frictional force is, in essence, the vector sum of many forces acting between the surface atoms of one body and those of another body.  "
 

When two ordinary surfaces are placed together, only the high points touch each other. (It is like having the Alps of Switzerland turned over and placed down on the Alps of Austria.) The actual microscopic area of contact is much less than the apparent macroscopic contact area, perhaps by a factor of 10,000

how it works at a microscopic level

H&R CH6 Friction

what influences friction:

  • the surface structure of the material
  • the downward pressure (force)
  • the deformability of the materials

how it works at a microscopic level

H&R CH6 Friction

what influences friction:

  • the surface structure of the material
  • the downward pressure (force)
  • the deformability of the materials

why? both those factors determine how much surface is actually in contact between the 2 bodies: more surface in contact, more vectors to sum

H&R CH6 Friction

name a material with high friction

H&R CH6 Friction

name a material with high friction

name a material with low friction

The Coefficient of friction is different for different materials in contact

The Coefficient of cannot be derived from principles, it is measured experimantally

the coefficient of friction between 2 materials measures the magnitude of the friction

the coefficient of friction essentially measures the total surface of contact between 2 surfaces taking into account the microscopic structure and deformability of the surfaces

Frictional properties of rubber

https://nvlpubs.nist.gov/nistpubs/jres/28/jresv28n4p439_A1b.pdf

Static Friction is greater than dynamic friction for speeds appreciably less than 0.001 cm/sec and less than dynamic friction for greater speeds

The  coefficients decrease slightly with increasing pressure and are independent f the size of the specimen (within a specific regime)

https://racingspot.pirelli.com/global/en-ww/race/when-it-s-time-to-change-from-slick-to-wet-tyres-in-formula-1

maximize surface

removes water

There is actually a specific rolling friction coefficient fr

https://threerockbooks.com/friction-and-rock-climbing/

different stones

mathematical properties of friction

\vec{F} = -\vec{f}

  1. If the body does not move, then the static frictional force fs and the component of F that is parallel to the surface balance each other. They are equal in magnitude, and fs is directed opposite that component of F

H&R CH6 Friction

mathematical properties of friction

\vec{F} = -\vec{f}
f_{s,\mathrm{max}} = \mu_s F_N

  1. If the body does not move, then the static frictional force fs and the component of F that is parallel to the surface balance each other. They are equal in magnitude, and fs is directed opposite that component of F

2.  The magnitude of fs has a maximum value fs,max  given by

 

      where μs is the coefficient of static friction and FN is the magnitude of the normal              force on the body from the surface.

      If the magnitude of the component of F: that is parallel to the surface exceeds fs,max,              then the body begins to slide along the surface.

H&R CH6 Friction

  1. If the body does not move, then the static frictional force fs and the component of F that is parallel to the surface balance each other. They are equal in magnitude, and fs is directed opposite that component of F

mathematical properties of friction

\vec{F} = -\vec{f}

2.  The magnitude of fs has a maximum value fs,max  given by

 

      where μs is the coefficient of static friction and FN is the magnitude of the normal              force on the body from the surface.

      If the magnitude of the component of F: that is parallel to the surface exceeds fs,max,              then the body begins to slide along the surface.

f_{s,\mathrm{max}} = \mu_s F_N
f_{k} = \mu_k F_N

3.   If the body begins to slide along the surface, the magnitude of the frictional                            force rapidly decreases to a value fk given by

 

      where μκ is the coefficient of kinetic friction.

mathematical properties of friction

H&R CH6 Friction

Drag and air resistance

A fluid is anything that can flow, gas or a liquid.

When there is a relative velocity between a fluid and a body the body experiences a drag force D that opposes the relative motion and points in the direction in which the fluid flows relative to the body.

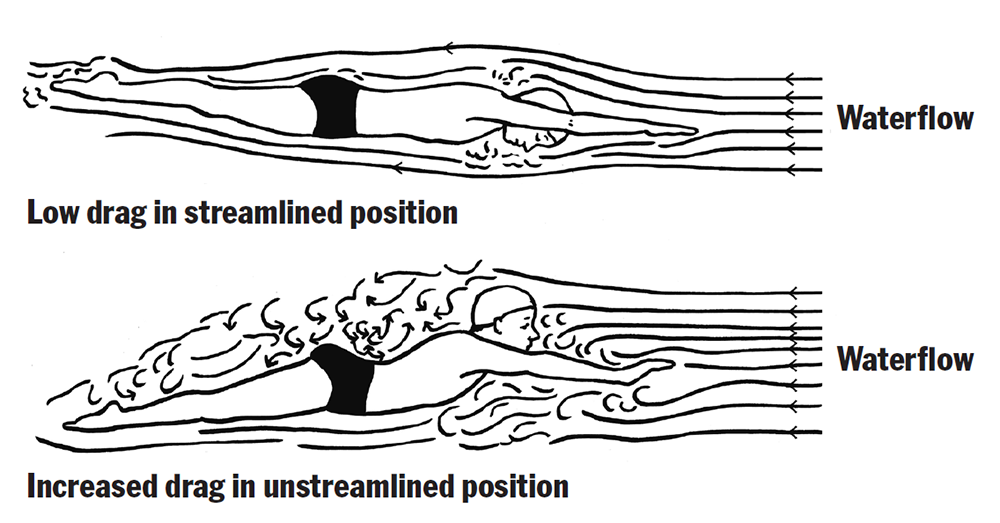
H&R CH6 Friction

Drag and air resistance

A fluid is anything that can flow, gas or a liquid.

When there is a relative velocity between a fluid and a body the body experiences a drag force D that opposes the relative motion and points in the direction in which the fluid flows relative to the body.

the magnitude of the drag force D is related to the relative speed v by an experimentally determined drag coefficient C according to

 

no turbolence

D = \frac{1}{2}C\rho Av^2

H&R CH6 Friction

Drag and air resistance

D = \frac{1}{2}C\rho Av^2

proportional to the area A of the body

H&R CH6 Friction

Drag and air resistance

D = \frac{1}{2}C\rho Av^2

proportional to the area A of the body

effective cross-sectional area

H&R CH6 Friction

Drag and air resistance

D = \frac{1}{2}C\rho Av^2

proportional to the density of the fluid ρ

H&R CH6 Friction

Drag and air resistance

D = \frac{1}{2}C\rho Av^2

proportional to the velocity of the body v

H&R CH6 Friction

Drag and air resistance

D = \frac{1}{2}C\rho Av^2

proportional to the velocity of the body v

\frac{1}{2}C\rho A v_t^2 - Fg = 0\\ v_t = \sqrt{\frac{2 F_g}{C\rho A}}

terminal velocity: a falling body reached a constant speed

H&R CH6 Friction

KEY POINTS:

H&R CH6 Friction

(see https://slides.com/federicabianco/phys20713_5#/16​ for circular motion)

F = m|a| = m\frac{|v_c|^2}{r}
F \propto \frac{1}{r}

circular motion

H&R CH6 Friction