PHYS 207.013
Chapter 8
potential energy
conservation of energy
Instructor: Dr. Bianco
TAs: Joey Betz; Lily Padlow
University of Delaware - Spring 2021



Energy
- kinetic energy
- work
-Potential energy -conservation of energy
H&R CH8 potential energy - conservation of energy
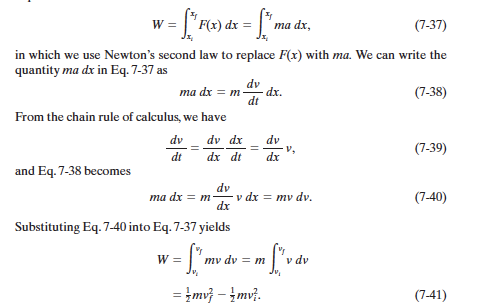
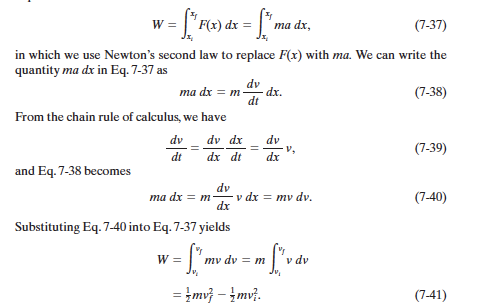
Instantaneous Work
H&R CH8 potential energy - conservation of energy
Instantaneous Work
H&R CH8 potential energy - conservation of energy
[N m]
Instantaneous Work
H&R CH8 potential energy - conservation of energy
kinetic energy
[N m]
Instantaneous Work
H&R CH8 potential energy - conservation of energy
kinetic energy
[N m]
Instantaneous Work
H&R CH8 potential energy - conservation of energy
kinetic energy
[N m]
work-energy theorem
H&R CH8 potential energy - conservation of energy
A
B
h
W and K in 1D
v
H&R CH8 potential energy - conservation of energy
A
B
h
W and K in 1D
lift m from A to B
v
H&R CH8 potential energy - conservation of energy
A
B
h
W and K in 1D
W and K in 1D
H&R CH8 potential energy - conservation of energy
A
B
h
W and K in 3D
H&R CH8 potential energy - conservation of energy
W and K in 3D
H&R CH8 potential energy - conservation of energy

F
F
W and K in 3D
H&R CH8 potential energy - conservation of energy

F
F
At every step in the path:
W and K in 3D
H&R CH8 potential energy - conservation of energy

F
F
At every step in the path:
each piece is the 1D prob we did before
W and K in 3D
H&R CH8 potential energy - conservation of energy

F
F
At every step in the path:
W and K in 3D
H&R CH8 potential energy - conservation of energy

F
F
At every step in the path:
W and K in 3D
slightly more practical
H&R CH8 potential energy - conservation of energy

F
F
h
W and K in 3D
slightly more practical
H&R CH8 potential energy - conservation of energy

F
F
h
only force is g: acts along y
W and K in 3D
slightly more practical
H&R CH8 potential energy - conservation of energy

F
F
h
But this does not depend on the crazy path I took!!
W and K in 3D
slightly more practical
H&R CH8 potential energy - conservation of energy

F
h
But this does not depend on the crazy path I took!!

W and K in 3D
slightly more practical
H&R CH8 potential energy - conservation of energy

F
h
But this does not depend on the crazy path I took!!

Instantaneous Work
H&R CH8 potential energy - conservation of energy
If the Work done by a Force does not depend on the path taken that force is said to be conservative
Conservative Forces
H&R CH8 potential energy - conservation of energy
If the Work done by a Force does not depend on the path taken that force is said to be conservative
- e.g. Gravity is conservative
can you think of a non conservative force and another non conservative force?
Conservative Forces
H&R CH8 potential energy - conservation of energy
If the Work done by a Force does not depend on the path taken that force is said to be conservative
- e.g. Gravity is conservative
can you think of a non conservative force and another non conservative force?
CONSERVATIVE: Gravity - Spring
NON-CONSERVATIVE: Friction
Conservation of Mechanical Energy
H&R CH8 potential energy - conservation of energy
A
A
B
h
lift m from A to B
v
Conservation of Mechanical Energy
H&R CH8 potential energy - conservation of energy
A
A
B
h
lift m from A to B
Conservation of Mechanical Energy
H&R CH8 potential energy - conservation of energy
A
A
B
h
lift m from A to B
Conservation of Mechanical Energy
H&R CH8 potential energy - conservation of energy
A
A
B
h
lift m from A to B
The sum of potential energy and kinetic energy remains the same
when the force is conservative
call mgy Potential Energy
use the letter U to refer to it
the 0 point of the potential gravitational energy
H&R CH8 potential energy - conservation of energy
A
A
this point is arbitrary: the only thing that matters is the distance h - just be consistent!
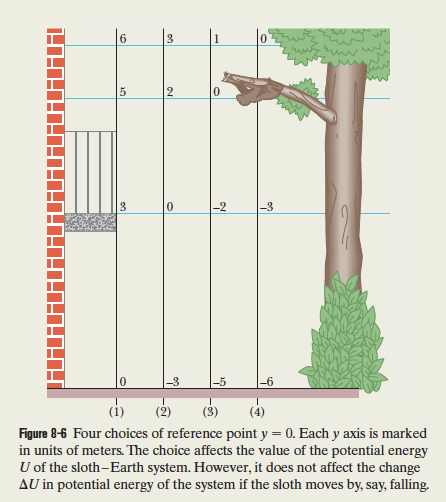
A
B
0
h
the 0 point of the potential gravitational energy
H&R CH8 potential energy - conservation of energy
A
A
this point is arbitrary: the only thing that matters is the distance h - just be consistent!

A
B
-h
0
the 0 point of the potential gravitational energy
H&R CH8 potential energy - conservation of energy
A
A
this point is arbitrary: the only thing that matters is the distance h - just be consistent!

A
B
h
2h
0
Conservation of Elastic Energy
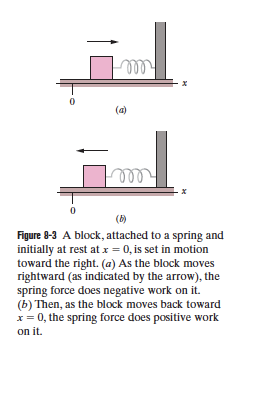

loop-the-loop problem
H&R CH8 potential energy - conservation of energy

loop-the-loop problem
H&R CH8 potential energy - conservation of energy


will a ball released from the top left of this track make it around the loop?
H&R CH8 potential energy - conservation of energy

A
B
C
D
E
loop-the-loop problem
H&R CH8 potential energy - conservation of energy


A
C
D
E
everywhere
B
loop-the-loop problem
H&R CH8 potential energy - conservation of energy


A
B
C
D
E
everywhere
loop-the-loop problem
H&R CH8 potential energy - conservation of energy


A
B
C
D
E
loop-the-loop problem
H&R CH8 potential energy - conservation of energy


A
B
C
D
E
loop-the-loop problem
H&R CH8 potential energy - conservation of energy


A
B
C
D
E
pendulum problem
H&R CH8 potential energy - conservation of energy

what can you immediately say about the height a pendulum will reach on the opposite side of the initial release point?
pendulum problem
H&R CH8 potential energy - conservation of energy

what can you immediately say about the height a pendulum will reach on the opposite side of the initial release point?
how high can it go?
pendulum problem
H&R CH8 potential energy - conservation of energy

what can you immediately say about the height a pendulum will reach on the opposite side of the initial release point?
how high can it go?
why will it eventually stop?
Conservation of Energy
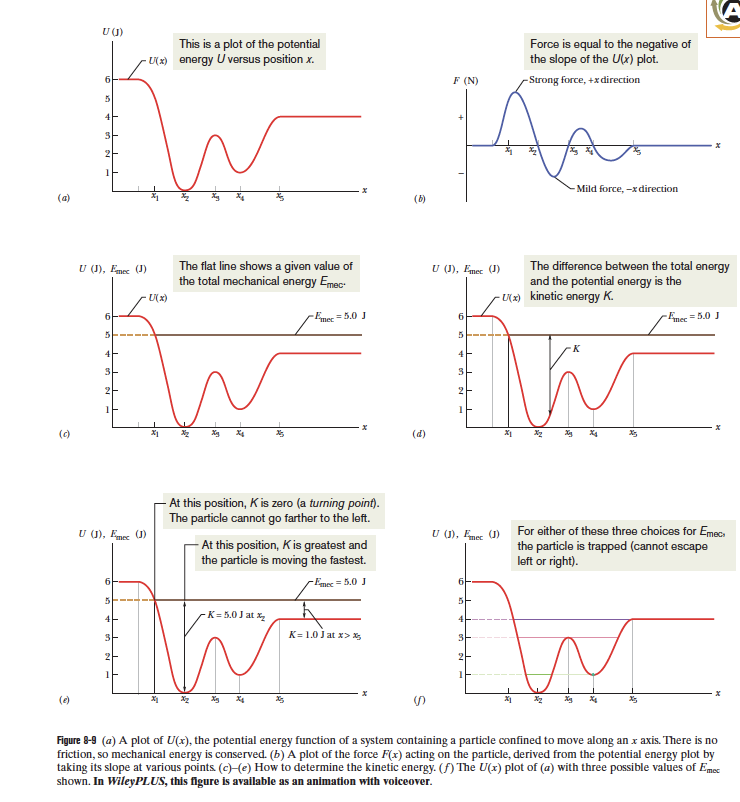
Conservation of Energy


Conservation of Energy



slope U < 0
=> F > 0
Turning point: K = 0
U=E
particle changes direction

if the system is isolated and only contains conservative forces
Conservation of Energy

slope U < 0
=> F > 0
Turning point: K = 0
U=E
particle changes direction

if the system is isolated and only contains conservative forces
Conservation of Energy



Neutral Equilibrium: U + Emec
K = 0
dU/dx = F = 0
if the system is isolated and only contains conservative forces
Conservation of Energy

K(x)=0
K(d+dx)>0
K(d-dx)>0
Unstable equilibrium: U=E
K=0
particle would start moving if displaced


if the system is isolated and only contains conservative forces
Conservation of Energy

U = Emec
U(x+/- dx) > Emec
Stable equilibrium:
U = E
particle cannot move without violating K>0


if the system is isolated and only contains conservative forces
Non conservative forces

exercise: think about how the examples we saw earlier, pendulum, loop-the-loop would change if we included non-conservative forces in the problem
KEY POINTS:


- Gravitational potential energy:
- Hooks potential energy
-
The potential energy relates to the force
-
in absence of non conservative forces, for an isolated system, the mechanical energy is conserved

potential energy and
conservation of energy
H&R CH7 kinetic energy and work