principles of Urban Science 5

dr.federica bianco | fbb.space |    fedhere |    fedhere

machine learning 

 

 

this slide deck:

 

https://slides.com/federicabianco/pus2020_7

 
 

what is machine learning

 

machine learning best practices

 

issues in data ethics

 

epistemic transparency

 

where does the bias enter models

 

what is machine learning?

1

 

a model is a low dimensional representation of a higher dimensionality datase

the best way to think about it    in the ML context:

 

what is a model?

what is machine learning?

[Machine Learning is the] field of study that gives computers the ability to learn without being explicitly programmed.

Arthur Samuel, 1959

 

what is machine learning?

model

parameters: slope, intercept

[Machine Learning is the] field of study that gives computers the ability to learn without being explicitly programmed.

Arthur Samuel, 1959

 

what is machine learning?

[Machine Learning is the] field of study that gives computers the ability to learn without being explicitly programmed.

Arthur Samuel, 1959

 

model

parameters: slope, intercept

data

 

what is machine learning?

ML: any model with parameters learnt from the data

Machine Learning models are parametrized representation of "reality"  where the parameters are learned from finite sets of realizations of that reality

(note: learning by instance, e.g. nearest neighbours, may not comply to this definition)

Machine Learning is the disciplines that conceptualizes, studies, and applies those models.

Key Concept

what is  machine learning?

 

used to:

  • understand structure of feature space
  • classify based on examples,
  • regression (classification with infinitely small classes)
  • understand which features are important in prediction (to get close to causality)

General ML points

unsupervised vs supervised learning

Clustering

partitioning the feature space so that the existing data is grouped (according to some target function!)

Clustering

partitioning the feature space so that the existing data is grouped (according to some target function!)

Unsupervised learning

  • understanding structure  
  • anomaly detection
  • dimensionality reduction

All features are observed for all datapoints

unsupervised vs supervised learning

Clustering

partitioning the feature space so that the existing data is grouped (according to some target function!)

Classifying & regression

 

finding functions of the variables that allow to predict unobserved properties of new observations

Unsupervised learning

  • understanding structure  
  • anomaly detection
  • dimensionality reduction

All features are observed for all datapoints

unsupervised vs supervised learning

Clustering

partitioning the feature space so that the existing data is grouped (according to some target function!)

Classifying & regression

 

finding functions of the variables that allow to predict unobserved properties of new observations

Unsupervised learning

  • understanding structure  
  • anomaly detection
  • dimensionality reduction

All features are observed for all datapoints

unsupervised vs supervised learning

Clustering

partitioning the feature space so that the existing data is grouped (according to some target function!)

Classifying & regression

 

finding functions of the variables that allow to predict unobserved properties of new observations

Unsupervised learning

  • understanding structure  
  • anomaly detection
  • dimensionality reduction

Supervised learning

  • classification
  • prediction
  • feature selection

All features are observed for all datapoints

Some features are not observed for some data points we want to predict them.

unsupervised vs supervised learning

Unsupervised learning

Supervised learning

All features are observed for all datapoints

and we are looking for structure in the feature space

Some features are not observed for some data points we want to predict them.

The datapoints for which the target feature is observed are said to be "labeled"

Semi-supervised learning

Active learning

A small amount of labeled data is available. Data is cluster and clusters inherit labels

The code can interact with the user to update labels.

also...

unsupervised vs supervised learning

what is machine learning?

extract features and create models that allow prediction where the correct answer is known for a subset of the data

supervised learning

identify features and create models that allow to understand structure in the data

unsupervised learning

  • k-Nearest Neighbors

  • Regression

  • Support Vector Machines

  • Neural networks

  • Classification/Regression Trees

  • clustering

  • Principle Component Analsysis

  • Apriori (association rule)

train, test, and validate

2

validating a model

How do we measure if a model is good?

Accuracy

Precision

Recall

ROC

AOC

 

We will talk more about this later...

but for now focus on

regression performance metrics

validating a model

How do we measure if a model is good?

Accuracy

Precision

Recall

ROC

AOC

 

Absolute error

 

 

Squared error

 

 

Mean squared error

 

 

Root mean

squared error

 

Relative mean

squared error

 

R squared

​

SE = \sum_i\epsilon_i^2
MSE = \frac{1}{N}SE
RMSE=\sqrt{MSE}
rMSE = \frac{MSE}{\sigma^2}
R^2 = 1 - rMSE
AE = \sum_i|\epsilon_i|
\epsilon_i=y_𝑖 - f(t_i)

We will talk more about this later...

but for now focus on

regression performance metrics

validating a model

How do we measure if a model is good?

Accuracy

Precision

Recall

ROC

AOC

 

Absolute error

 

 

Squared error

 

 

Mean squared error

 

 

Root mean

squared error

 

Relative mean

squared error

 

R squared

​

SE = \sum_i\epsilon_i^2
MSE = \frac{1}{N}SE
RMSE=\sqrt{MSE}
rMSE = \frac{MSE}{\sigma^2}
R^2 = 1 - rMSE
AE = \sum_i|\epsilon_i|

do you recognize these??

\epsilon_i=y_𝑖 - f(t_i)

We will talk more about this later...

but for now focus on

regression performance metrics

validating a model

How do we measure if a model is good?

Accuracy

Precision

Recall

ROC

AOC

 

We will talk more about this later...

but for now focus on

regression performance metrics

\epsilon_i=y_𝑖 - f(t_i)

Split the sample in test and training sets 

Train on the training set

Test (measure accuracy) on the test set

R^2 = 1 - rMSE

validating a model

from sklearn.model_selection import train_test_split

def line(x, intercept, slope):
    return slope * x + intercept

def chi2(args, x, y, s):
    a, b = args
    return sum((y - line(x, a, b))**2 / s)

x_train, x_test, y_train, y_test, s_train, s_test = train_test_split(
     x, y, s, test_size=0.25, random_state=42)

initialGuess = (10, 1)

chi2Solution_goodsplit = minimize(chi2, initialGuess, 
	args=(x_train, y_train, s_train))

print("best fit parameters from the minimization of the chi squared: " + 
       "slope {:.2f}, intercept {:.2f}".format(*chi2Solution_goodsplit.x))

print("R square on training set: ", Rsquare(chi2Solution_goodsplit.x, x_train, y_train))
print("R square on test set: ", Rsquare(chi2Solution_goodsplit.x, x_test, y_test))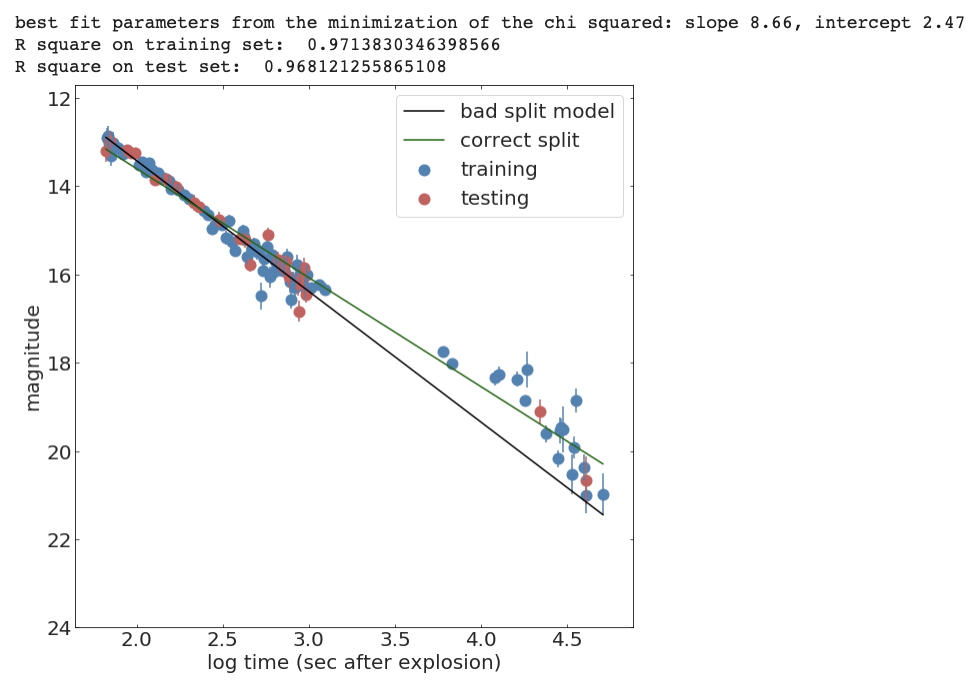

validating a model

validating a model

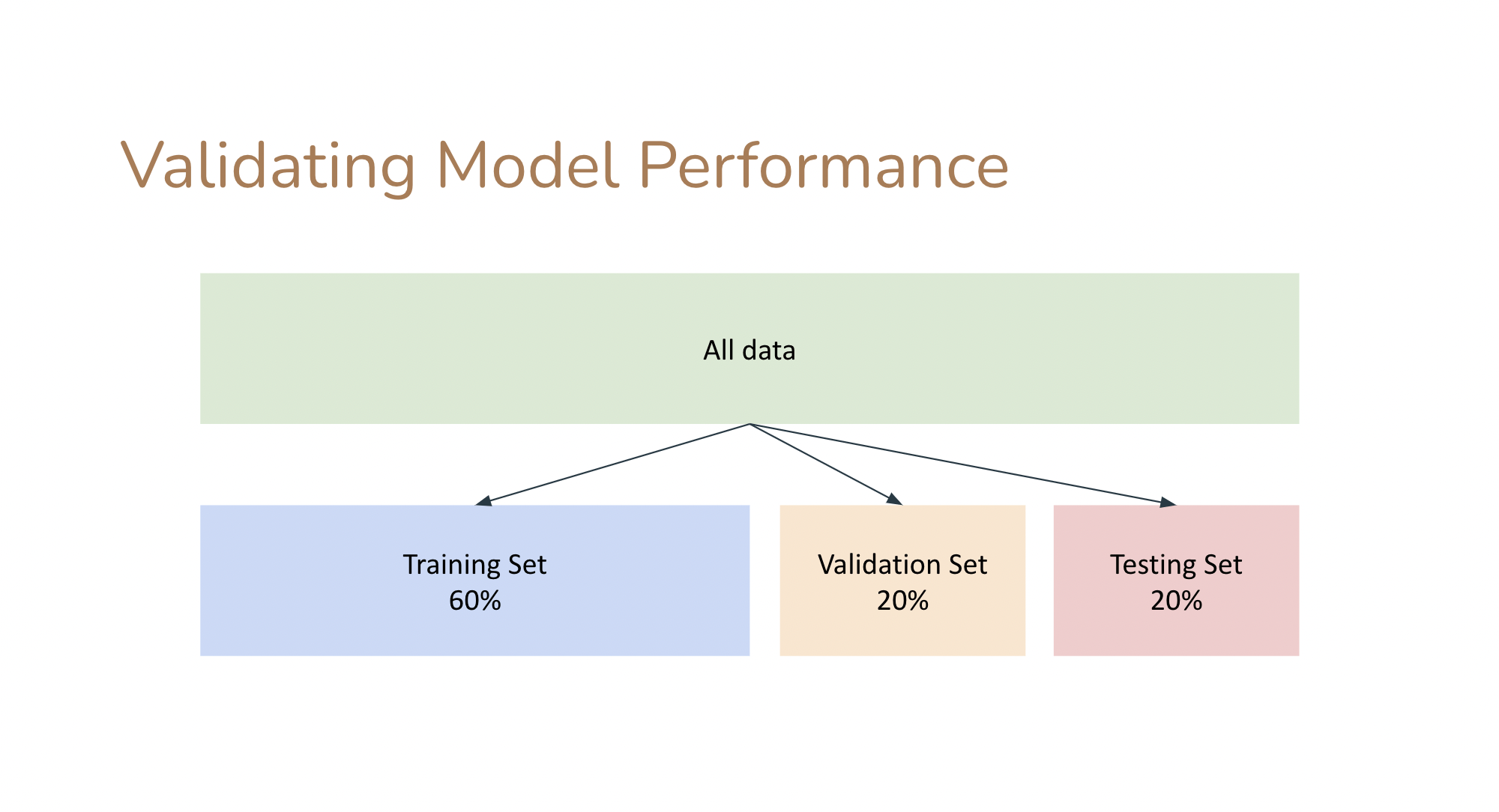
validating a model

Cross validation

test train validation

train parameters on training set

run only once on the test set to assess the model performance

Cross validation

test + train + validation

train parameters on training set

adjust parameters on validation set

run only once on the test set to assess the model performance

Cross validation

k-fold cross validation

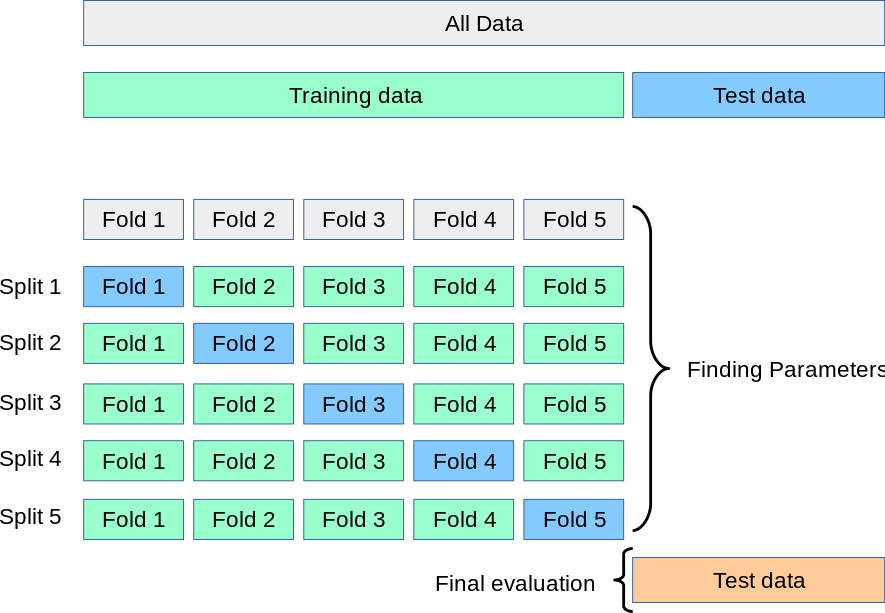
Cross validation

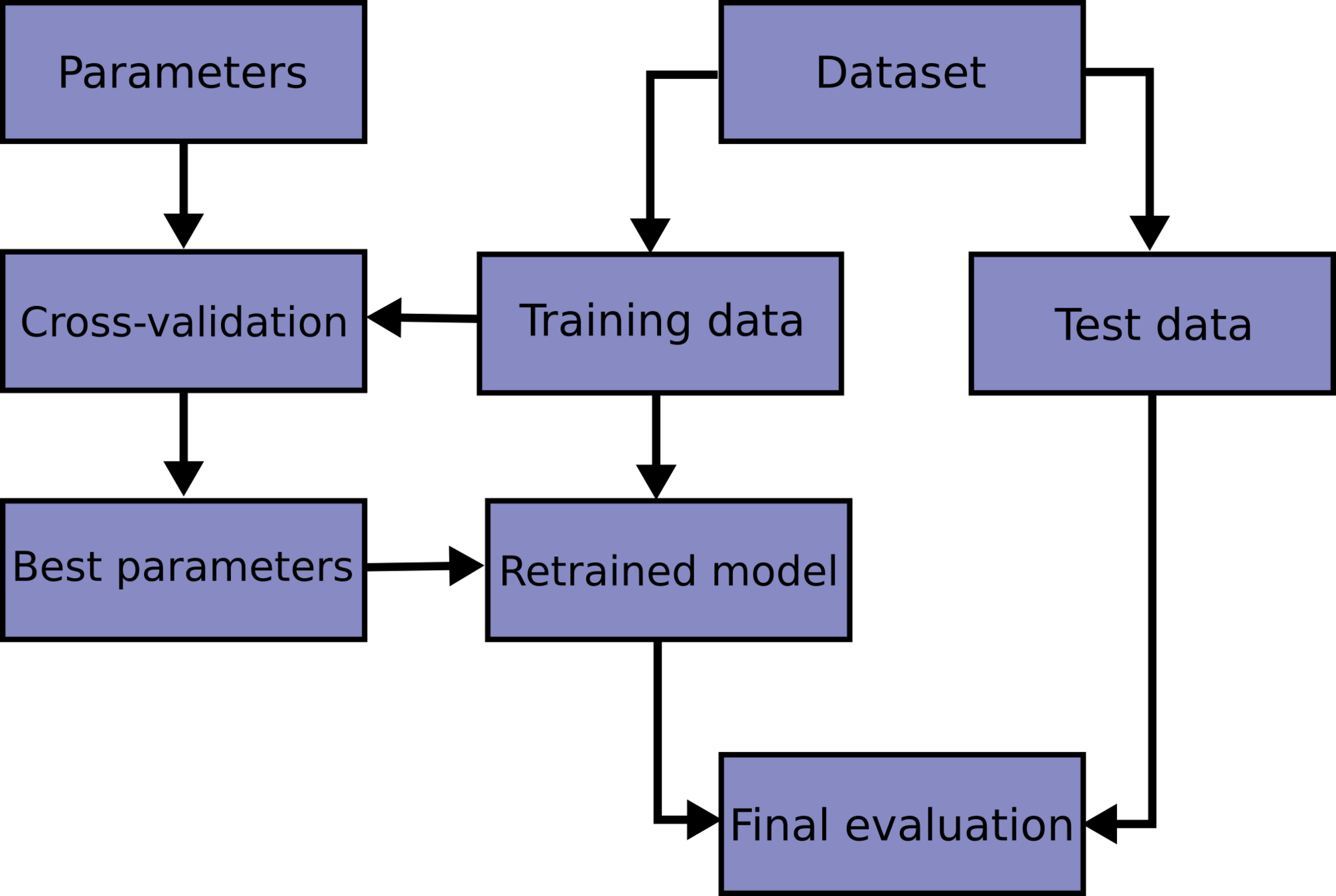
https://scikit-learn.org/stable/modules/cross_validation.html

Model Selection

methods

2.2

ML standard

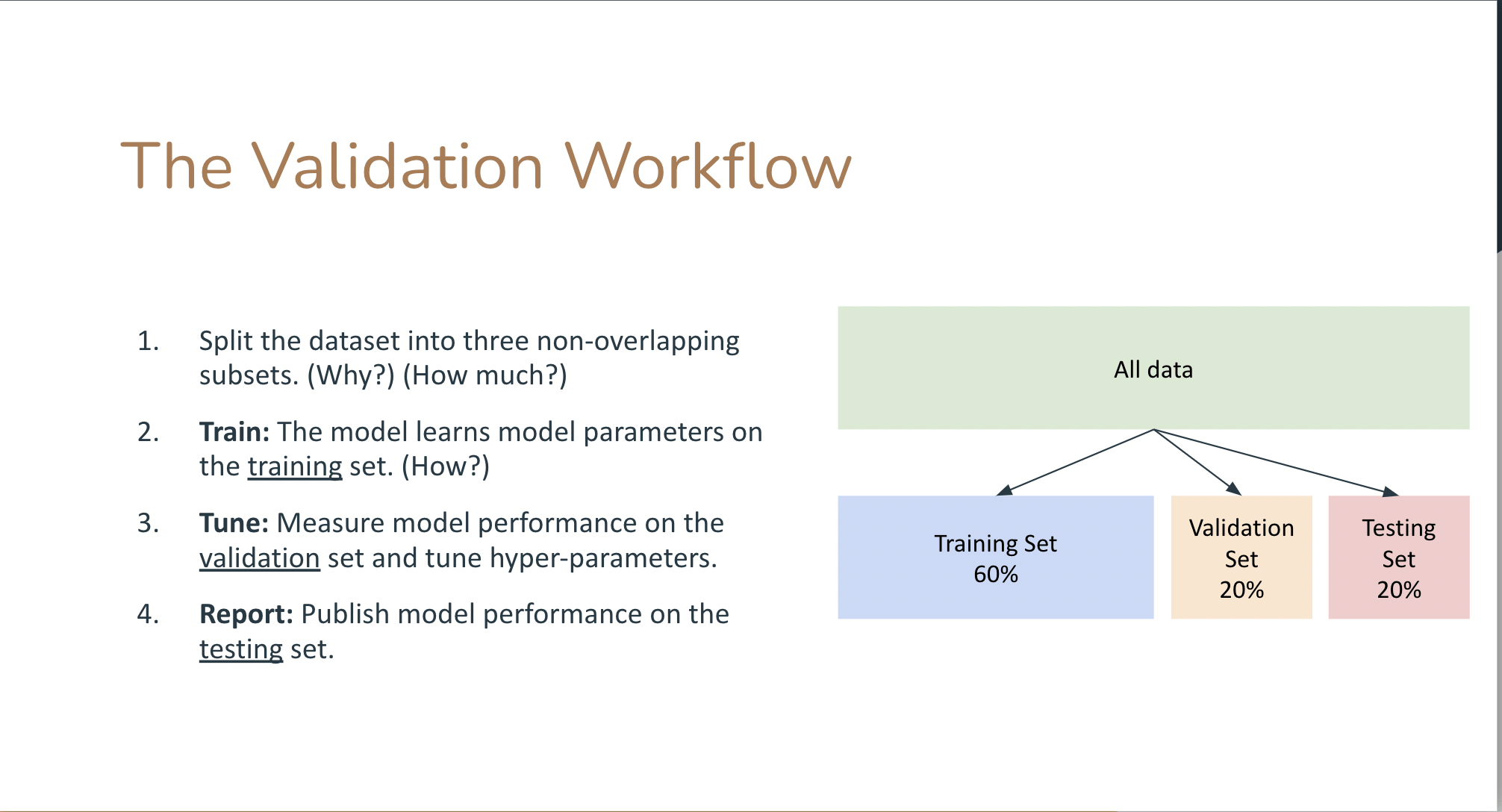
In ML models need to be "validated":

  1. split the data into a training and a test set (typical split 70/30). 
  2. learn the model parameters by "training" the model on the training set
  3. "test" the model on the test set: measure the accuracy of the prediction (e.g. as the distance between the prediction and the test data).

The performance on the model is the performance achieved on the test set.  

An upgrade on this workflow is to create a training, a test, and a validation test. Iterate between training and test to achieve optimal performance, then measure accuracy on the validation set.This is because you can use the test set performance to tune the model hyperparameters (model selection) but then you would report a performance that is tuned on the test set.

a significance performance degradation on the test compared to training set indicates that the model is "overtrained" and does not generalize well.

Model Selection

methods

2.2

HOW DO I CHOOSE A MODEL?

Given two models which is preferable?

 

Likelihood-ratio tests

 likelihood ratio statistics LR

LR = -2 log_e \frac{L\mathrm{(simple~model)}}{L\mathrm{(complex~model})}

NESTED MODELS : one model contains the other one, e.g.

y= mx + l 

is contained in

y=ax**2+ mx + l

 

statsmodels.model.compare_lr_ratio()

A rigorous answer (in terms of NHST) can be obtained for 2 nested models

This directly answers the question:

“is my more complex model overfitting the data?”

The LR statistics is expected to follow a χ^2 distrbution under the Null Hypothesis that the simpler model is preferable

HOW DO I CHOOSE A MODEL?

Given two models which is preferable?

 

Likelihood-ratio tests

NESTED MODELS : one model contains the other one, e.g.

y= mx + l 

is contained in

y=ax**2+ mx + l

 

A rigorous answer (in terms of NHST) can be obtained for 2 nested models

This directly answers the question:

“is my more complex model overfitting the data?”

The LR statistics is expected to follow a χ^2 distrbution under the Null Hypothesis that the simpler model is preferable

from scipy.stats.distributions import chi2
def likelihood_ratio(llmin, llmax):
    return(-2*(llmax-llmin))

LR = likelihood_ratio(L1,L2)

p = chi2.sf(LR, dof) 
# dof: difference in number of parameters 
print ('p: %.30f' % p)
# LR is chi squared distributed: 
# p represents the probability that this result
# (or a more extreme result than this)
# would happen by chance

HOW DO I CHOOSE A MODEL?

Given two models which is preferable?

 

Likelihood-ratio tests

 likelihood ratio statistics LR

LR = -2 log_e \frac{L\mathrm{(complex~model)}}{L\mathrm{(simple~model})}

statsmodels.model.compare_lr_ratio()

The LR statistics is expected to follow a χ^2 distrbution under the Null Hypothesis that the simpler model is preferable

difference in number of parameters between the 2 models

MLTSA:

model selection

Shannon 1948: A Mathematical Theory of Communication

a theory to find fundamental limits on signal processing and communication operations such as data compression 

 

model selection is also based on the minimization of a quantity. Several quantities are suitable: 

 

MLD

BIC

Bayese theorem

AIC

Optimism and likelihood maximization on the training set

MLTSA:

AIC, BIC, & MDL

{\displaystyle {\text{AIC}}=-\frac{2}{N}\log(L)+\frac{2}{N}k} %=\\ {\displaystyle AIC+(2(p+q+k)(p+q+k+1))/(T-p-q-k-1).}

number of parameters: 

Model Complexity

Likelihood: Model Performance.

Akaike information criterion (AIC) .

Based on 

where                 is a family of function (=densities) containing the correct (=true) function and    is the set of parameters that maximized the likelihood L

L is the likelihood of the data, k is the number of parameters,

N the number of variables.

 

\hat{\theta}
\lim_{N\to\infty} (-2 E(\log Pr_{\hat{\theta}}(Y)) ) = -\frac{2}{N} E ~\log(L) + d\frac{2}{N}
Pr_{\hat{\theta}}(Y)

MLTSA:

AIC, BIC, & MDL

{\displaystyle {\text{AIC}}=-\frac{2}{N}\log(L)+\frac{2}{N}k} %=\\ {\displaystyle AIC+(2(p+q+k)(p+q+k+1))/(T-p-q-k-1).}

number of parameters: 

Model Complexity

Likelihood: Model Performance.

\hat{\theta}

"-" sign in front of the log-likelihood:  AIC shrinks for better models,

AIC ~ k => is linearly proportional to the number of parameters  

Akaike information criterion (AIC) .

Based on 

where                 is a family of function (=densities) containing the correct (=true) function and    is the set of parameters that maximized the likelihood L

L is the likelihood of the data, k is the number of parameters,

N the number of observations.

 

\lim_{N\to\infty} (-2 E(\log Pr_{\hat{\theta}}(Y)) ) = -\frac{2}{N} E ~\log(L) + \frac{2}{N}d
Pr_{\hat{\theta}}(Y)

MLTSA:

AIC, BIC, & MDL

{\displaystyle {\text{BIC}}=-2\log(L)+\log(N)k} %=\\ {\displaystyle AIC+(2(p+q+k)(p+q+k+1))/(T-p-q-k-1).}

Likelihood: Model Performance.

number of parameters: 

Model Complexity

Bayesian information criterion (BIC) .

L is the likelihood of the data, k is the number of parameters,

N the number of observations.

stronger penalization of complexity (as long as N>     )

e^2

The derivation is very different: 

\frac{P(M_m | D)}{P(M_l | D)} = \frac{P(M_m)}{P(M_l)}\cdot\frac{P(D|M_m)}{P(D|M_l)}

Bayes Factor

MLTSA:

AIC, BIC, & MDL

{\displaystyle {\text{MDL}}= -\log(L(\theta)) – \log(L(y | X, \theta))} %=\\ {\displaystyle AIC+(2(p+q+k)(p+q+k+1))/(T-p-q-k-1).}

Minimum Description Length (MDL) .

negative log-likelihood of the model parameters (θ) and the negative log-likelihood of the target values (y) given the input values (X) and the model parameters (θ).

also: log(L(θ)): number of bits required to represent the model,

log(L(y| X,θ)): number of bits required to represent the predictions on observations

minimize the encoding of the model and its predictions

derived from Shannon's theorem of information

MLTSA:

AIC, BIC, & MDL

{\displaystyle {\text{MDL}}= -\log(L(\theta)) – \log(L(y | X, \theta))} %=\\ {\displaystyle AIC+(2(p+q+k)(p+q+k+1))/(T-p-q-k-1).}
{\displaystyle {\text{BIC}}=-2\log(L)+\log(N)k} %=\\ {\displaystyle AIC+(2(p+q+k)(p+q+k+1))/(T-p-q-k-1).}
{\displaystyle {\text{AIC}}=-\frac{2}{N}\log(L)+\frac{2}{N}k} %=\\ {\displaystyle AIC+(2(p+q+k)(p+q+k+1))/(T-p-q-k-1).}

Mathematically similar, though derived from different approaches. All used the same way: the preferred model is the model that minimized the estimator

implementation https://machinelearningmastery.com/probabilistic-model-selection-measures/

MLTSA:

AIC, BIC, & MDL

{\displaystyle {\text{MDL}}= -\log(L(\theta)) – \log(L(y | X, \theta))} %=\\ {\displaystyle AIC+(2(p+q+k)(p+q+k+1))/(T-p-q-k-1).}
{\displaystyle {\text{BIC}}=-2\log(L)+\log(N)k} %=\\ {\displaystyle AIC+(2(p+q+k)(p+q+k+1))/(T-p-q-k-1).}
{\displaystyle {\text{AIC}}=-\frac{2}{N}\log(L)+\frac{2}{N}k} %=\\ {\displaystyle AIC+(2(p+q+k)(p+q+k+1))/(T-p-q-k-1).}

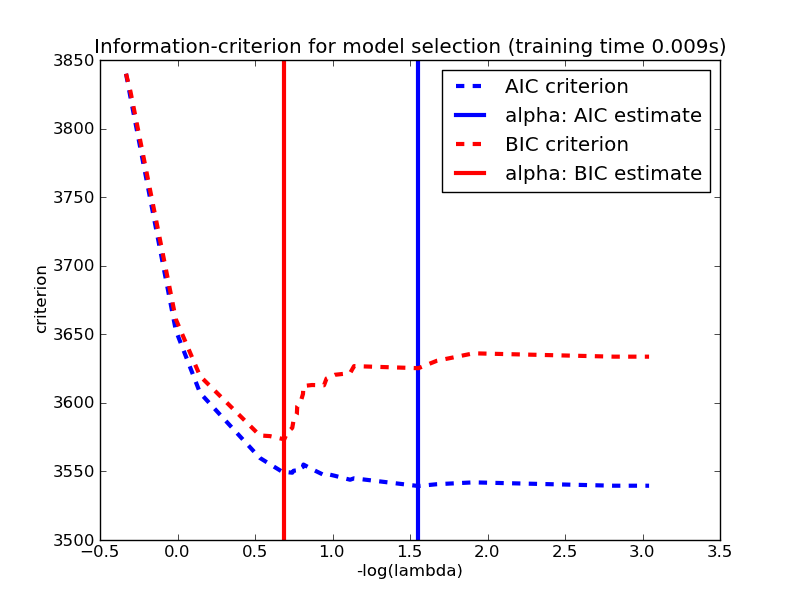
HOW DO I CHOOSE A MODEL?

Given two models which is preferable?

 

AIC - BIC

also consider at Akaike and Bayesian Information Criteria for not nested models: 

both are returned in a statsmodel fit

A rigorous answer (in terms of NHST) can be obtained for 2 nested models

This directly answers the question:

“is my more complex model overfitting the data?”

The LR statistics is expected to follow a χ^2 distrbution under the Null Hypothesis that the simpler model is preferable

https://www.methodology.psu.edu/resources/AIC-vs-BIC/

they are calculated combining the likelihood with a penalization for the extra parameters

generally both  decrease with increasing increasing likelihood but you would look for the place where they start decreasing slowly as the "sweet spot" for your model

the principle of parsimony

 

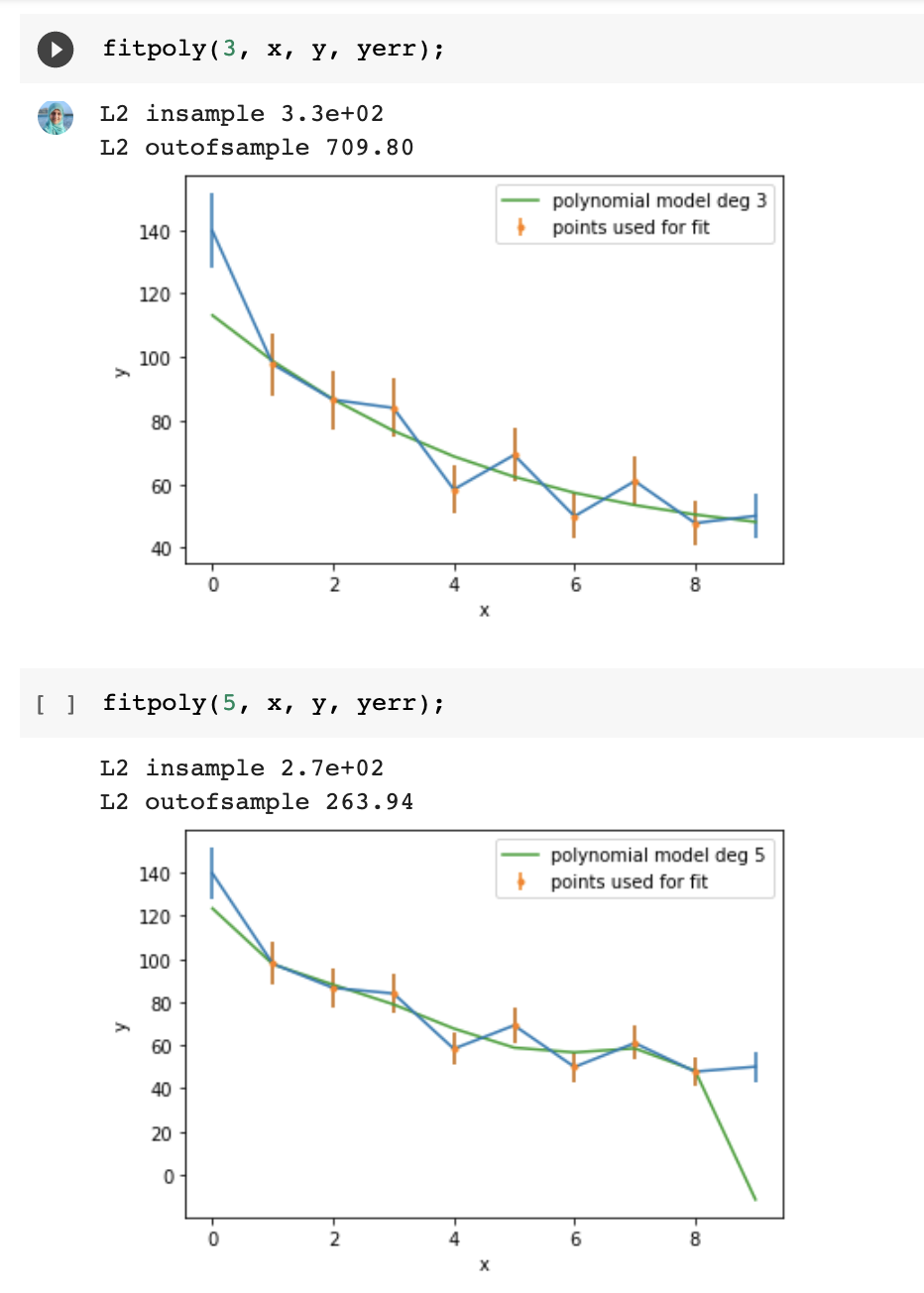
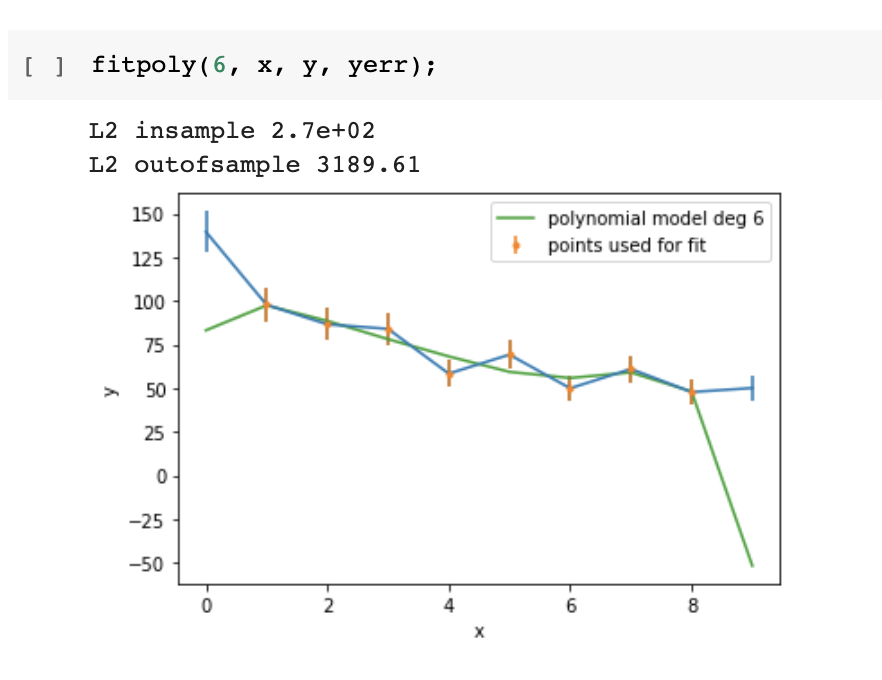
Careful!

Increasing the model's degrees freedom allows a "better fit" in the in-sample set

Logarithms

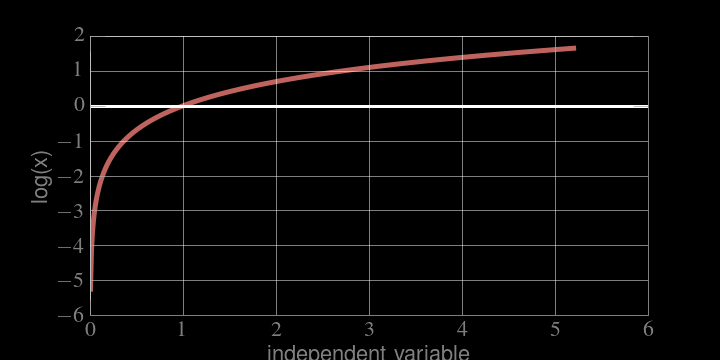
MONOTONICALLY INCREASING

 

if x grows, log(x) grows, if x decreases, log(x) decreases

the location of the maximum is the same!

Logarithms

 

 

SUPPORT :

(0,\infty]

MONOTONICALLY INCREASING

Logarithms

 

 

SUPPORT :

(0,\infty]

Not a problem cause L like P is positive defined

MONOTONICALLY INCREASING

likelihood, probability, and objective functions

L (m,b | \vec{y} ) = \prod_i^N p_i( y_i | x_i, m, b)
L (m,b | \vec{y} ) = \prod_i^N p_i( y_i | x_i, \sigma_i, m, b)
p(y_i) = \frac{1}{\sigma_i \sqrt{2\pi}} \exp{-\frac{(y_i - (mx_i + b))^2 }{2 \sigma_i^2}}
\ln{L (m,b | \vec{y} )} = K - \sum{\frac{(y_i - (mx_i + b) )^2}{2 \sigma_i^2}} = K - \frac{1}{2}\chi^2

The problem of fitting models to data reduces to finding the

maximum likelihood

of the data given the model

 

This is effectively done by finding the minimum of the

-log(likelihood)

Summary

data ethics

3

intended and unintended consequences

https://www.un.org/en/chronicle/article/ideology-racism-misusing-science-justify-racial-discrimination

https://www.technologyreview.com/2020/07/17/1005396/predictive-policing-algorithms-racist-dismantled-machine-learning-bias-criminal-justice/

Data Science is a black box

Models are neutral, data is biased

two dangerous data-ethics myths

Data Science is a black box

machine learning models are

Epistemic transparency

 

 

Right to explanation: the scope of a general "right to explanation" is a matter of ongoing debate

 

tration by Hanne Morstad 

Democratised AI — The Black Box Problem

 

Accountability: who is responsible if an algorithm does harm

algorithmic transparency

https://www.darpa.mil/attachments/XAIIndustryDay_Final.pptx

we are still trying to figure it out 

we are still trying to figure it out 

trivially intuitive

generalized additive models

decision trees

SVM

Random Forest

Deep Learning

Accuracy

univaraite

linear

regression

algorithmic transparency

#UDCSS2020

@fedhere​

algorithmic transparency

https://www.darpa.mil/attachments/XAIProgramUpdate.pdf

we are still trying to figure it out 

we are still trying to figure it out 

trivially intuitive

generalized additive models

decision trees

SVM

Random Forest

Deep Learning

Accuracy in solving complex problems

univaraite

linear

regression

algorithmic transparency

#UDCSS2020

@fedhere​

algorithmic transparency

we are still trying to figure it out 

we are still trying to figure it out 

trivially intuitive

generalized additive models

decision trees

Deep Learning

number of features that can be effectively included in the model

thousands

1

SVM

Random Forest

univaraite

linear

regression

https://www.darpa.mil/attachments/XAIProgramUpdate.pdf

algorithmic transparency

#UDCSS2020

@fedhere​

Accuracy in solving complex problems

algorithmic transparency

we are still trying to figure it out 

we are still trying to figure it out 

trivially intuitive

univaraite

linear

regression

generalized additive models

decision trees

Deep Learning

SVM

Random Forest

https://www.darpa.mil/attachments/XAIProgramUpdate.pdf

time

algorithmic transparency

#UDCSS2020

@fedhere​

Accuracy in solving complex problems

algorithmic transparency

1

Machine learning: any method that learns parameters from the data

http://www.statsguy.co.uk/brexit-voting-and-education/

2

The transparency of an algorithm is proportional to its complexity and the complexity of the data space

3

The transparency of an algorithm is limited by our own ability and preparedness to interpret it

Toward Interpretable Machine Learning, Samek+2003

algorithmic transparency

models are neutral, the bias is in the data

https://www.theverge.com/21298762/face-depixelizer-ai-machine-learning-tool-pulse-stylegan-obama-bias

Why does this AI model whitens Obama face?

Simple answer: the data is biased. The algorithm is fed more images of white people

Decide which model is appropriate (depends on data and question)

 

 

where is the bias?

1 - model selection

we are still trying to figure it out 

we are still trying to figure it out 

trivially intuitive

generalized additive models

decision trees

SVM

Random Forest

Deep Learning

Accuracy

univaraite

linear

regression

where is the bias?

Decide what your target function is

Machine learning models are functions that "learn" their parameters from the data.

They "learn" by minimizing or maximize some quantity. 

 

What should you minimize? 

 

https://towardsdatascience.com/machine-learning-fundamentals-via-linear-regression-41a5d11f5220

2 - cost function

where is the bias?

They "learn" by minimizing or maximize some quantity. 

 

What should you minimize? 

 

the hypothetical trolley problem suddenly is real

self-driving cars

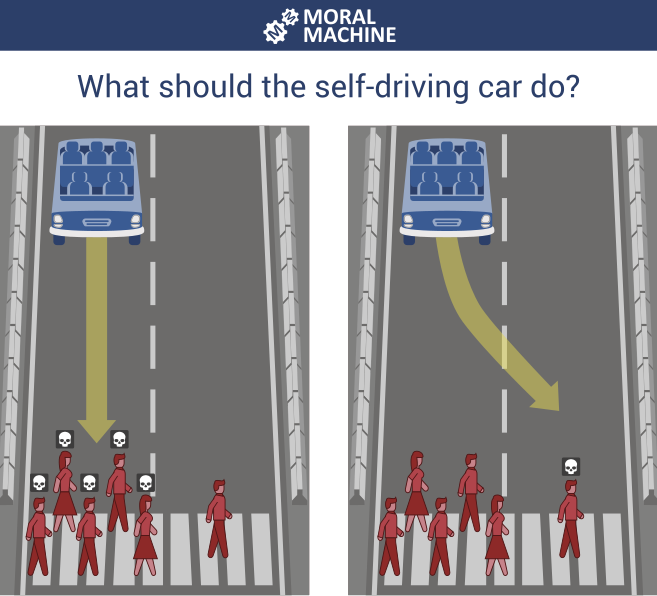
2 - cost function

where is the bias?

They "learn" by minimizing or maximize some quantity. 

 

What should you minimize? 

 

prosecutorial justice

https://theintercept.com/2020/07/12/risk-assessment-tools-bail-reform/

minimize number of people incarcerated injustly

maximize public safety

OR

2 - cost function

Explore the data

 

discover some of the bias

(trust me, there is more!)

it's not easy

there's covariance 

missing data

where is the bias?

3 - data selection and preparation

remove the bias...

(few try)

models are neutral, the bias is in the data

Should AI reflect

who we are

(and enforce and grow our bias)

or should it reflect who we aspire to be?

(and who decides what that is?)

models are neutral, the bias is in the data

The bias is in the data

Should AI reflect

who we are

(and enforce and grow our bias)

or should it reflect who we aspire to be?

(and who decides what that is?)

models are neutral, the bias is in the data

The bias is in the data

The bias is in the models and the decision we make

Should AI reflect

who we are

(and enforce and grow our bias)

or should it reflect who we aspire to be?

(and who decides what that is?)

models are neutral, the bias is in the data

The bias is in the data

The bias is in the models and the decision we make

The bias is in how we choose to optimize our model

Should AI reflect

who we are

(and enforce and grow our bias)

or should it reflect who we aspire to be?

(and who decides what that is?)

models are neutral, the bias is in the data

The bias is in the data

The bias is in the models and the decision we make

The bias is in how we choose to optimize our model

Should AI reflect

who we are

(and enforce and grow our bias)

or should it reflect who we aspire to be?

(and who decides what that is?)

The bias is society that provides the framework to validate our biased models

models are neutral, the bias is in the data

The bias is in the data

The bias is in the models and the decision we make

The bias is in how we choose to optimize our model

The bias is society that provides the framework to validate our biased models

Should AI reflect

who we are

(and enforce and grow our bias)

or should it reflect who we aspire to be?

(and who decides what that is?)

key concepts

MACHINE LEARNING

  • Machine Learning models are parametrized representation of "reality"  where the parameters are learned from finite sets of realizations of that reality
  • Unsupervised learning: all variables observed for all data, looking for natural grouping of datapoints in the N-dim space
  • Supervised learning: a target variable is known for (a subset of) the data and the goal is to predict it for new (the rest of the) data

DATA ETHICS

  • epistemic transparency:not all models are the same
  • there is a tradeoff between epistemic transparency and the ability to handle complex data
  • The bias enter data science in (at least) data; model selection; target function and optimization choices; validation

Text

references

homework

Midterm project due! 

12/20 (regular homework timeline, no other homework)

Write a project proposal for your final projefollowing 

this template