Bioestatística Aplicada

Prof. Fernando Sales

fernando.sales@ufpe.br

Bem, vamos voltar ao início...

Atividade 1

  1. Carregar o dataset "Pima.tr", disponível no pacote "MASS", distribuído com o R;
  2. Identificar quantas grávidas foram incluídas nesse dataset;
  3. Determinar quais foram os atributos selecionados e os respectivos tipos de variável [numérica, categórica,...]
  4. Façam os seguintes gráficos:
    1. Distribuição da quantidade de gestações por mulher;
    2. Distribuição de idade na amostra;
    3. Relação entre idade e quantidade de gestações
    4. Relação entre o IMC e a glicose
 
 
# loading MASS datasets
library(MASS)

# loading PIMA Women diabetes "training" dataset
data = Pima.tr
names(data) = names(Pima.tr)

# Primeiro, dê uma olhada na variável data na linha de comando

# Procure o comando para visualizar as primeiras linhas
#

Atividade 1

5. Faça uma tabela mostrando os seguintes valores de cada atributo na amostra:

  • Min, Max de cada atributo
  • Média, Moda e Mediana
  • Percentil 10, 25, 50, 75 e 90
  • Desvio-Padrão e Distância entre quartis

6. Refaça a tabela fazendo a divisão entre os grupos de diabéticas e não-diabéticas

 

 

 

# loading MASS datasets
library(MASS)

# loading PIMA Women diabetes "training" dataset
data = Pima.tr
names(data) = names(Pima.tr)

# Primeiro, dê uma olhada na variável data na linha de comando

# Procure o comando para visualizar as primeiras linhas
#

Atividade 1

7. Suponha que você deseja analisar a distribuição de frequências dos atributos não analisados anteriormente e que tenham valores numéricos. Que tipo de transformação nos dados seria interessante proceder antes de realizar o gráfico? Justifique.

 

8. Refaça os histogramas mudando a largura dos bins. Comente o que muda na distribuição.

 

9. Refaça os histogramas anteriores segregando a amostra em dois grupos de acordo com a presença de diabetes.

# loading MASS datasets
library(MASS)

# loading PIMA Women diabetes "training" dataset
data = Pima.tr
names(data) = names(Pima.tr)

# Primeiro, dê uma olhada na variável data na linha de comando

# Procure o comando para visualizar as primeiras linhas
#

Atividade 2

  1. Refaça todas as tarefas da atividade 1, para os datasets: Pima.tr2 e Pima.te
  2. Faça uma análise comparativa dos resultados obtidos para os valores dos atributos nos diferentes amostras

 

 

# loading MASS datasets
library(MASS)

# loading PIMA Women diabetes "training" dataset
data = Pima.tr
names(data) = names(Pima.tr)

# Primeiro, dê uma olhada na variável data na linha de comando

# Procure o comando para visualizar as primeiras linhas
#

Atividade 2

  1. Baixe o dataset: http://www.biostat.jhsph.edu/~rpeng/leanpub/rprog/chicago_data.zip
  2. Faça uma análise comparativa dos resultados obtidos para os valores dos atributos nos diferentes amostras

 

 

 
 
# loading MASS datasets
library(MASS)

# loading PIMA Women diabetes "training" dataset
data = Pima.tr
names(data) = names(Pima.tr)

# Primeiro, dê uma olhada na variável data na linha de comando

# Procure o comando para visualizar as primeiras linhas
#

Até mais!

Probabilidade

https://www.khanacademy.org/math/statistics-probability/probability-library/conditional-probability-independence/v/conditional-probability-tree-diagram-example

Uma empresa realiza um exame toxicológico no processo de seleção de seus novos funcionários. O teste específico que eles usam tem uma taxa de falsos positivos de 2% e uma taxa de falsos negativos de 1%. Supondo que 5% dos aplicantes usem drogas ilícitas e um deles seja selecionado aleatoriamente.

 

Dado que o teste seja positivo, qual é a probabilidade dele estar usando drogas?

Probabilidade Condicional

Suppose there are two bowls of cookies. Bowl 1contains 30 vanilla cookies and 10 chocolate cookies. Bowl 2 contains 20 of each. Now suppose you choose one of the bowls at random and, without looking, select a cookie at random. The cookie is vanilla. What is the probability that it came from Bowl 1?

\boxed{p(A|B) = \cfrac{p(A \cap B)}{p(B)}}

Cap. 1, Think Bayes, Allen Downey http://greenteapress.com/wp/think-bayes/

\begin{aligned} &a) \enspace p(Bowl\,1)\, =\, ?\\ &b) \enspace p(vanilla\,|\, Bowl\,1)\, =\, ?\\ &c) \enspace p(chocolate\,|\, Bowl\,2)\, =\, ?\\ &d) \enspace p(vanilla)\, =\, ?\\ &e) \enspace p(chocolate)\, =\, ? \end{aligned}

Probabilidade Condicional

Suppose there are two bowls of cookies. Bowl 1contains 30 vanilla cookies and 10 chocolate cookies. Bowl 2 contains 20 of each. Now suppose you choose one of the bowls at random and, without looking, select a cookie at random. The cookie is vanilla. What is the probability that it came from Bowl 1?

Cap. 1, Think Bayes, Allen Downey http://greenteapress.com/wp/think-bayes/

\boxed{ \def\arraystretch{1.5} \begin{array}{c:c:c} \, & V & C \\ \hline B1 & 30 & 10 \\ \hdashline B2 & 20 & 20 \end{array}}
\boxed{p(\text{Bowl\,1}\,|\,\text{vanilla})\, =\, \cfrac{p(\text{Bowl\,1}\, \cap \text{vanilla})}{p(\text{vanilla})}}

Probabilidade Condicional

Suppose there are two bowls of cookies. Bowl 1contains 30 vanilla cookies and 10 chocolate cookies. Bowl 2 contains 20 of each. Now suppose you choose one of the bowls at random and, without looking, select a cookie at random. The cookie is vanilla. What is the probability that it came from Bowl 1?

Cap. 1, Think Bayes, Allen Downey http://greenteapress.com/wp/think-bayes/

Testes diagnósticos - Definições

  • Sensibilidade (S+) - Probabilidade de um teste dar positivo para uma amostra positiva;

  • Especificidade (S-) - Probabilidade de um teste dar negativo para uma amostra negativa;

  • Acurácia (AC) - Probabilidade de um teste classificar adequadamente uma amostra, isto é, classificar como positiva uma amostra positiva ou como negativa, caso contrário;

  • Taxa de Falsos Negativos (FNR) - Probabilidade de um teste dar negativo para uma amostra positiva;

  • Taxa de Falsos Positivos (FPR) - Probabilidade de um teste dar positivo para uma amostra negativa;

Testes diagnósticos - Definições

  • Valor Preditivo Positivo (PPR) - Probabilidade de uma amostra ser positiva dado o resultado do teste é positivo;

  • Valor Preditivo Negativo (NPR) - Probabilidade de uma amostra ser negativa dado o resultado do teste é negativo;

Testes diagnósticos

\boxed{ \def\arraystretch{1.5} \begin{array}{c:c:c} \, & P & N \\ \hline T^{+}\,[P] & VP & FP \\ T^{-}\,[N] & FN & VN \end{array}}

Padrão-Ouro

Teste

\begin{aligned} \boxed{S^{+}=p(T^{+}|P)=\cfrac{VP}{VP+FN}}& \\ \boxed{S^{-}=p(T^{-}|N)=\cfrac{VN}{VN+FP}}& \\ \boxed{A_{c}=p(T^{+}|P)p(P)+p(T^{-}|N)p(N)}& \\ \boxed{FPR\,=p(T^{+}|N)=\cfrac{FP}{FP+VN}}& \\ \boxed{FNR\,=p(T^{-}|P)=\cfrac{FN}{VP+FN}}& \\ \end{aligned}
\bold{\text{Legenda:} \enspace} \begin{aligned} &P:\, Positivo\\ &N:\, Negativo\\ &T^{+}:\, Teste Positivo\\ &T^{-}:\, Teste Negativo\\ \end{aligned}

Razão de Verossimilhança

  • Definição: razão entre a probabilidades de um evento acontecer em uma população portadora da doença e a probabilidade dele acontecer numa população não portadora;

\begin{aligned} &RV^{+}=\cfrac{p(T^{+}|P)}{p(T^{+}|N)}=\cfrac{S^{+}}{1-S^{-}} \\ &RV^{-}=\cfrac{p(T^{-}|P)}{p(T^{-}|N)}=\cfrac{1-S^{+}}{S^{-}} \\ \end{aligned}

Aplicações - Epidemiologia

  • Incidência - Razão entre a quantidade de novos casos da doença e a quantidade de pessoas expostas;

  • Prevalência - Quantidade de pessoas com a doença [condição] na população;

  • Taxa de Mortalidade - Proporção de pessoas que morreram por uma dada causa na população [em um período de tempo];

  • Letalidade - Proporção de pessoas que morreram por uma dada doença [causa] na população infectada [afetada pela causa];

Aplicações - Epidemiologia

  • Risco Relativo - Razão entre a probabilidade do grupo que tem o fator de risco desenvolver a condição-alvo e a probabilidade do grupo que não tem o fator de risco desenvolver a condição-alvo;

\begin{aligned} &RR=\cfrac{p(P|\text{Exposto})}{p(P|\text{Não\,Exposto})}=\cfrac{I_{E}}{I_{\bar{E}}}=\cfrac{I_{\text{Exposto}}}{I_{\text{Não\,Exposto}}}\\ \end{aligned}

  • Utilidade: Identificação de fatores de risco [RR > 1] ou fatores protetores [RR < 1] em relação a condição em estudo. Muito utilizado na área cardiovascular, sendo muitos resultados obtidos do Framingham Heart Study [70 ANOS!!!]

A famosa COORTE...

Aplicações - Epidemiologia

  • Para determinar esses diversos índices, diferentes desenhos de estudo são possíveis. Caso tenham mais interesse no tema, procurem ler sobre:

    • Estudos Longitudinais

    • Estudos Transversais

    • Estudos de Coorte

    • Estudos Caso - Controle

    • Estudos de Prevalência

  • Sobre os índices da página anterior, reflitam sobre como seriam necessários estudos para inferir os parâmetros definidos lá.

Razão de Chances - Odds Ratio (OR)

  • Nem sempre é possível estimar a incidência de uma dada doença num grupo a partir do desenho do mesmo. Entretanto, é possível fazer uma estimativa em função das chances de uma determinada condição ser desenvolvida nos diferentes grupos da amostra, caso e controle.

\def\arraystretch{1.5} \begin{array}{c:c:c} Grupo & P & N \\ \hline Caso\, & a & b \\ Ctrl\, & c & d \\ \end{array} \\
\begin{aligned} &RV^{+}=\cfrac{p(P|\text{Caso})}{p(P|\text{Ctrl})}=\cfrac{\frac{a}{a+b}}{\frac{c}{c+d}}=\cfrac{a(c+d)}{c(a+b)}\\ &RV^{-}=\cfrac{p(N|\text{Caso})}{p(N|\text{Ctrl})}=\cfrac{\frac{b}{a+b}}{\frac{d}{c+d}}=\cfrac{b(c+d)}{d(a+b)}\\ &OR= \cfrac{RV^{+}}{RV^{-}}=\cfrac{ad}{bc}\\ \end{aligned}

Razão de Chances - Odds Ratio (OR)

  • Nem sempre é possível estimar a incidência de uma dada doença num grupo a partir do desenho do mesmo. Entretanto, é possível fazer uma estimativa em função das chances de uma determinada condição ser desenvolvida nos diferentes grupos da amostra, caso e controle.

\def\arraystretch{1.5} \begin{array}{c:c:c} Grupo & P & N \\ \hline Caso\, & a & b \\ Ctrl\, & c & d \\ \end{array} \\
\begin{aligned} &RV^{+}=\cfrac{p(P|\text{Caso})}{p(P|\text{Ctrl})}=\cfrac{\frac{a}{a+b}}{\frac{c}{c+d}}=\cfrac{a(c+d)}{c(a+b)}\\ &RV^{-}=\cfrac{p(N|\text{Caso})}{p(N|\text{Ctrl})}=\cfrac{\frac{b}{a+b}}{\frac{d}{c+d}}=\cfrac{b(c+d)}{d(a+b)}\\ &OR= \cfrac{RV^{+}}{RV^{-}}=\cfrac{ad}{bc}\\ \end{aligned}

Distribuições de Probabildade

 

Distribuição Binomial (Bernoulli)

Premissas:

  1. Número fixo de ensaios (n), cada um resulta em dois resultados mutuamente exclusivos;
  2. Os resultados dos n ensaios são independentes;
  3. A probabilidade de sucesso (p) para cada ensaio é constante;
P(X=x)=\dbinom{n}{x}p^{x}(1-p)^{n-x},\,\text{onde:\,}\dbinom{n}{x}=\cfrac{n!}{x!(n-x)!}

Distribuição Binomial (Bernoulli)

Exemplo 1: Uma moeda não viciada é utilizada num jogo de cara e coroa "sofisticado" composto por múltiplos lançamentos. Suponha que a moeda seja lançada n vezes em sequência.

a. Seja n = 3. Qual é a probabilidade do número de caras ser igual a zero? Igual a 1? Igual a 2? Igual a 3?

b. Seja n=10. Qual é a probabilidade do número de caras ser igual ao de coroas? E maior? E menor?

c. O que acontece com os casos anteriores se a moeda for trocada por uma moeda cuja probabilidade de cara for igual a 0,7?

P(X=x)=\dbinom{n}{p}p^{x}(1-p)^{n-x},\,\text{onde:\,}\dbinom{n}{p}=\cfrac{n!}{p!(n-p)!}

Distribuição Binomial (Bernoulli)

Exemplo 1: Uma moeda não viciada é utilizada num jogo de cara e coroa "sofisticado" composto por múltiplos lançamentos. Suponha que a moeda seja lançada n vezes em sequência.

a. Seja n = 3. Qual é a probabilidade do número de caras ser igual a zero? Igual a 1? Igual a 2? Igual a 3?

b. Seja n=10. Qual é a probabilidade do número de caras ser igual ao de coroas? E maior? E menor?

c. O que acontece com os casos anteriores se a moeda for trocada por uma moeda cuja probabilidade de cara for igual a 0,7?

P(X=x)=\dbinom{n}{p}p^{x}(1-p)^{n-x},\,\text{onde:\,}\dbinom{n}{p}=\cfrac{n!}{p!(n-p)!}

Observação [Binômio de Newton]

(a+b)^n=\sum\limits_{k=0}^n \dbinom{n}{p}a^{k}\,b^{n-k}
[p+(1-p)]^n=\sum\limits_{k=0}^n \dbinom{n}{p}p^{k}\,(1-p)^{n-k}=\sum\limits_{k=0}^n P(X=k)
\sum\limits_{k=0}^n P(X=k) = (p+1-p)^{n}=1^{n}=1

Fernando J R Sales

Contato: fernando.sales@ufpe.br | secretaria@sbeb.org.br

Um pouco da minha história...

http://bit.ly/cadastroST903

Vamos nos conhecer?

QUEM É você SEM dizer
O QUE você FAZ?

Respondam no chat...

Sobre o FUTURO do trabalho...

Fonte: http://reports.weforum.org/future-of-jobs-2016/chapter-1-the-future-of-jobs-and-skills/

Future of Work Report

Forum Econômico Mundial - 2016

McKinsey Quarterly

Where machines could replace humans—and where they can’t (yet). Jun 2016

Fonte: https://www.mckinsey.com/business-functions/digital-mckinsey/our-insights/where-machines-could-replace-humans-and-where-they-cant-yet

Sobre o FUTURO do trabalho...

Fonte: http://reports.weforum.org/future-of-jobs-2016/chapter-1-the-future-of-jobs-and-skills/

Future of Work Report

Forum Econômico Mundial - 2016

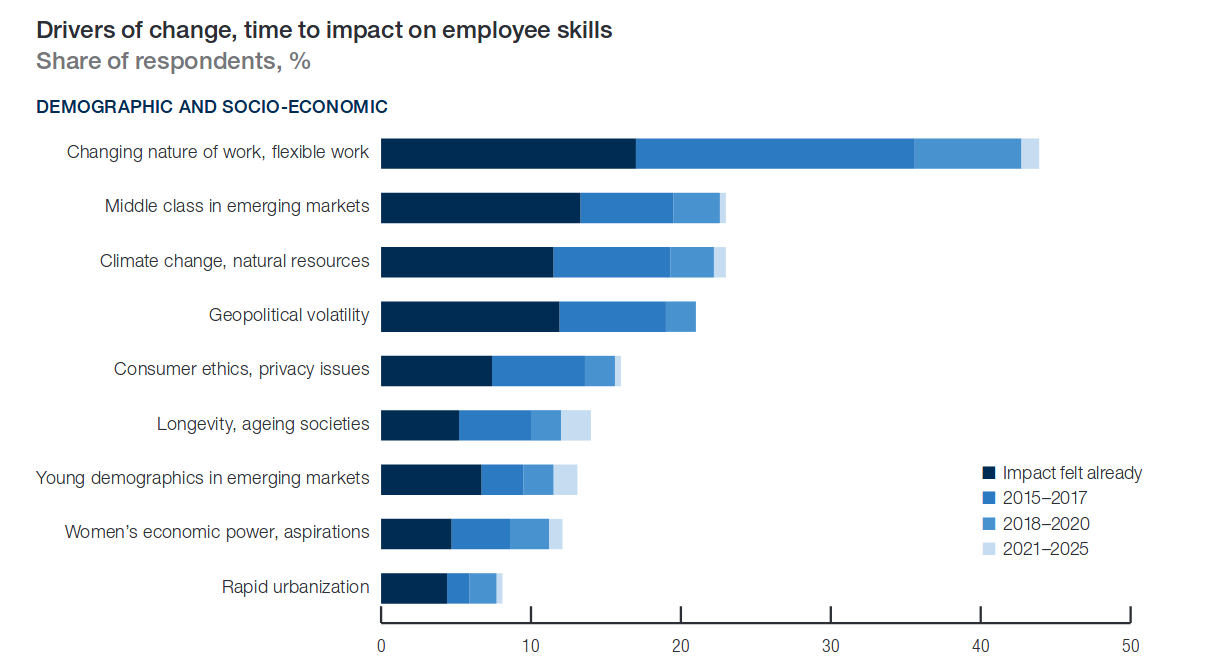
Sobre o FUTURO do trabalho...

Fonte: http://reports.weforum.org/future-of-jobs-2016/chapter-1-the-future-of-jobs-and-skills/

Future of Work Report

Forum Econômico Mundial - 2016

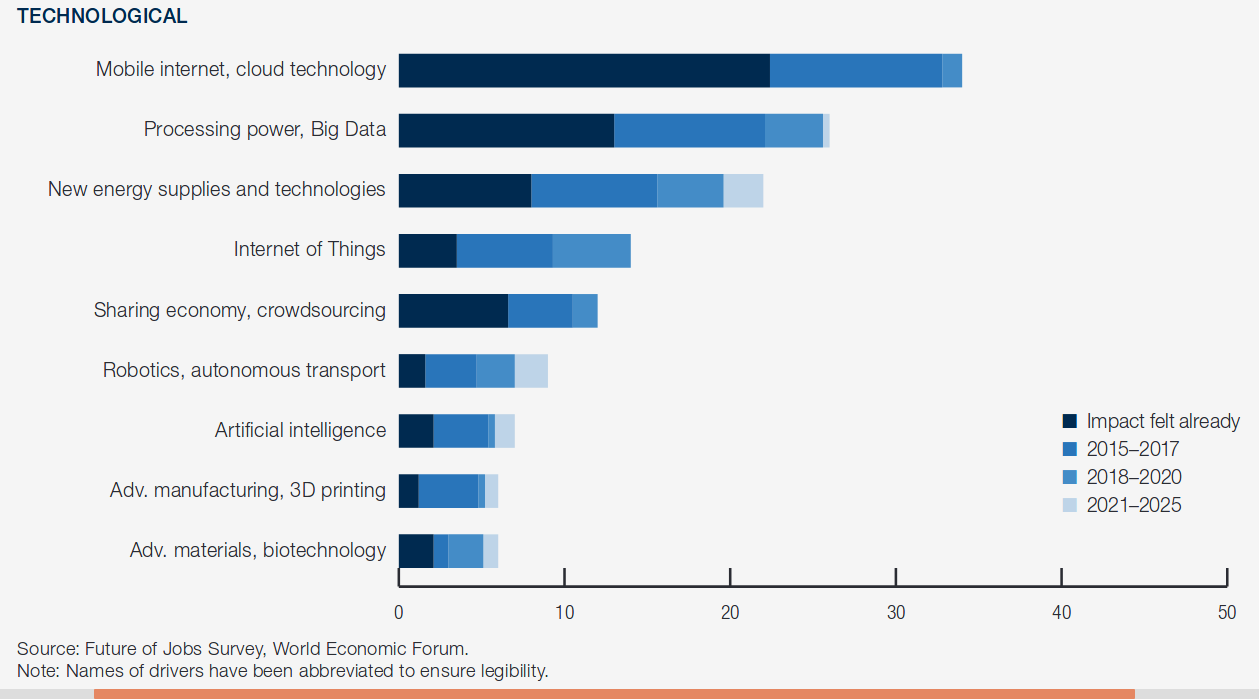
Sobre o FUTURO do trabalho...

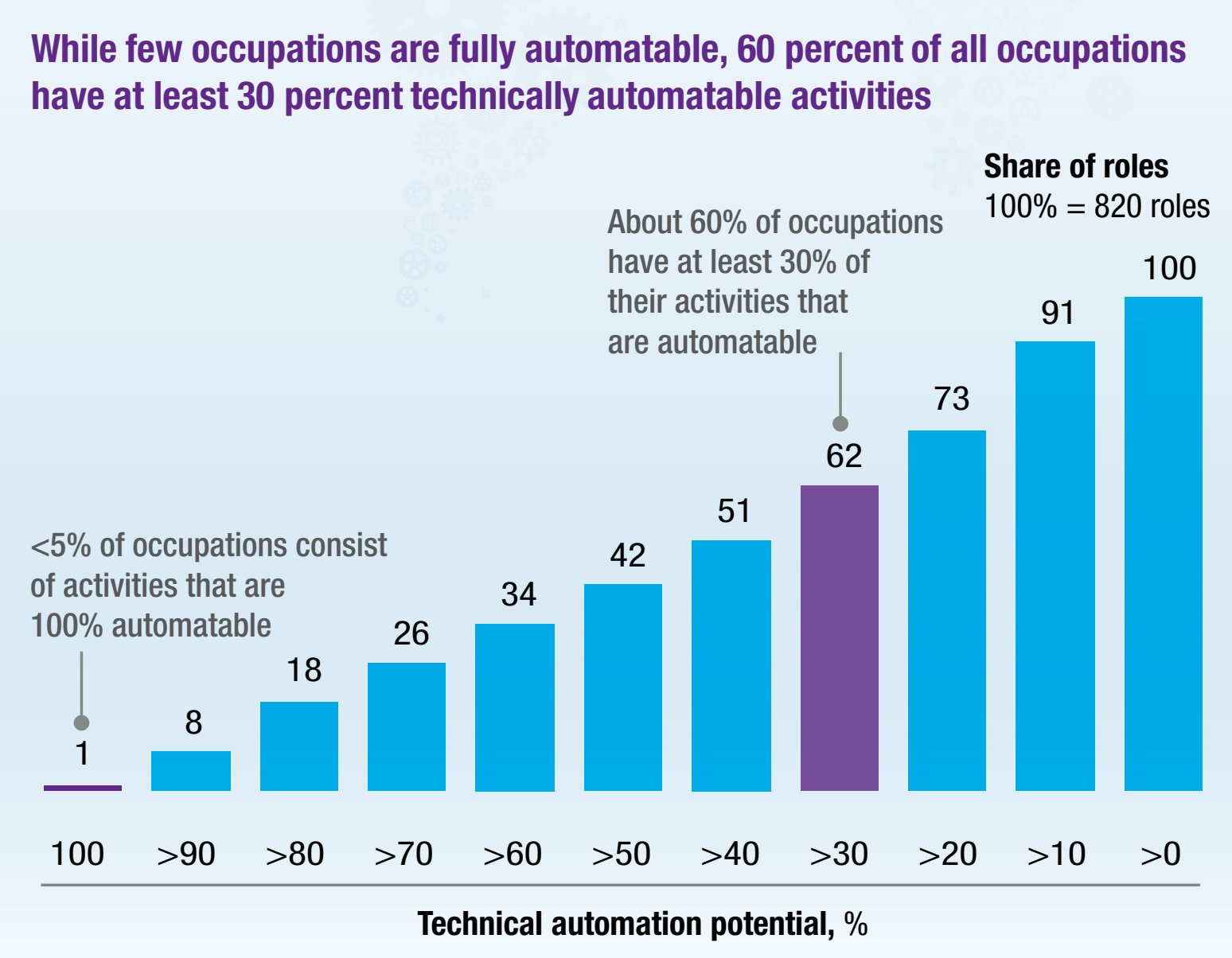
https://www.mckinsey.com/featured-insights/future-of-work/jobs-lost-jobs-gained-what-the-future-of-work-will-mean-for-jobs-skills-and-wages

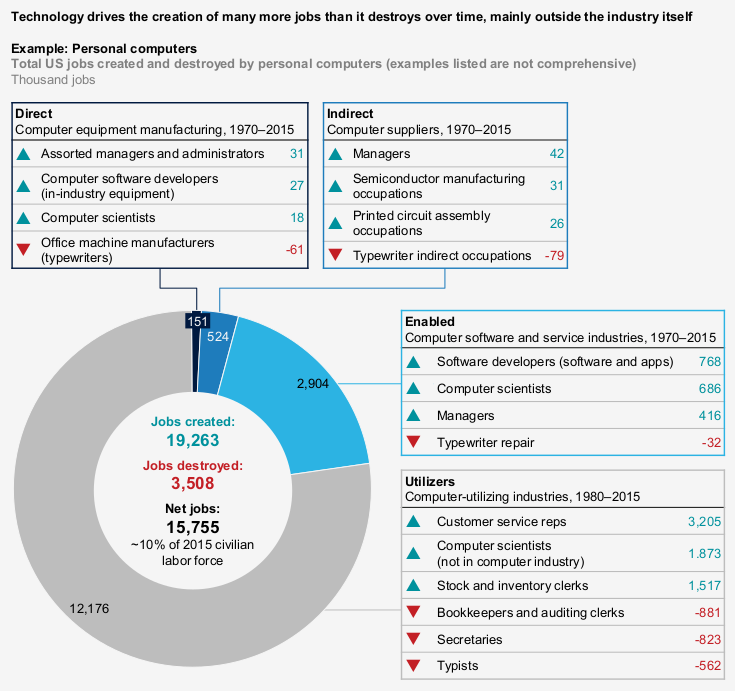
#TECH: Destrói mas  CRIA novos...

Sobre o #FUTURO:

Novas necessidades,

novas oportunidades!

 

Title Text

Subtitle

"O ANALFABETO do século XXI não será aquele que não consegue LER e ESCREVER, mas aquele que não consegue APRENDER, DESAPRENDER, e REAPRENDER." Alvin Toffler

"Learn to trust the journey, even when you don't know it."

Lolly Daskal

"Se você quer chegar rápido, vá sozinho. Se quiser chegar longe, vá em equipe."  Provérbio Africano

"The future is already here — it's just not very evenly distributed."

William Gibson

Os tempos mudam...

“INOVAÇÃO é a mudança do comportamento dos agentes no mercado, como fornecedores e consumidores [produtos, serviços...]”

Peter Drucker

 

Dados...[Facebook?]...Médicos!

Os Assistentes Pessoais...

Será?

https://cdn-images-1.medium.com/max/1600/0*wNFF7lH8QyswBM6X.png

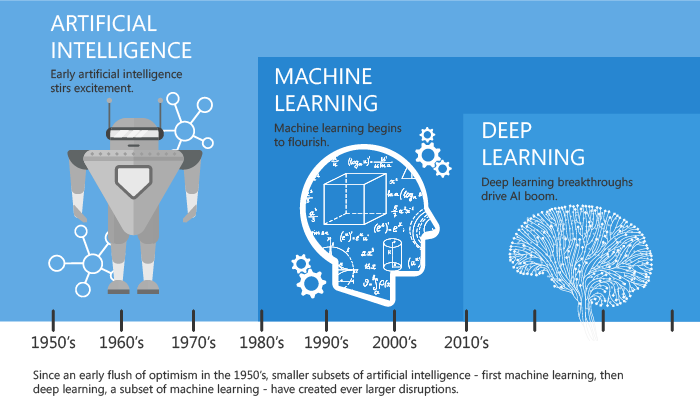
AI, Machine Learning, Deep Learning

AI, Machine Learning, Deep Learning

https://arxiv.org/pdf/1707.01836

AI, Machine Learning, Deep Learning

https://research.google.com/pubs/archive/45732.pdf

AI, Machine Learning, Deep Learning

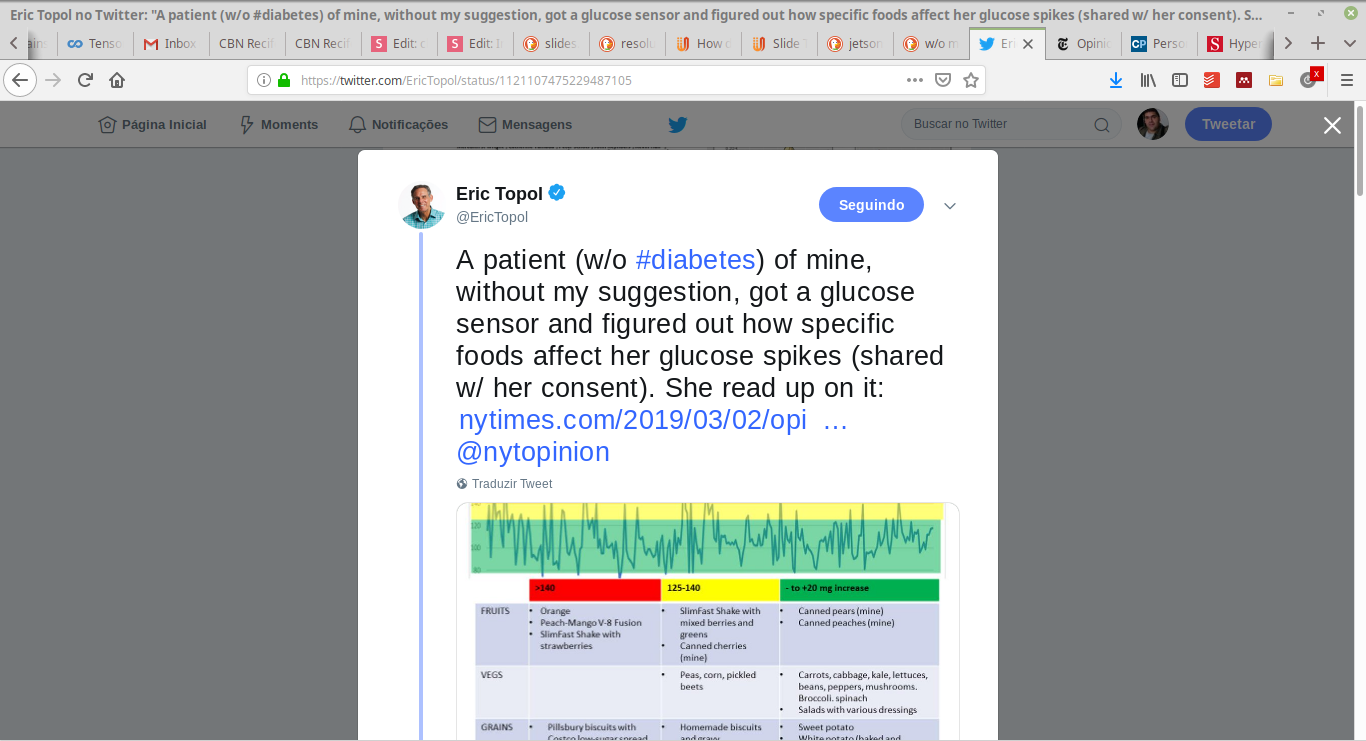
m-Health, Wearables, Big Data...

Sobre o FUTURO...

Premissa(s)

Hipótese

Experimentos

Resultados

Discussão

Conclusão

Tópicos Chave

Onde é o Início?

COVID-19

  • O que sabemos?
    • Doença mais complexa do que parecia...?
    • Diferentes fases
  • Diferentes abordagens terapêuticas baseadas em:
    • ​Antirretrovirais
    • Azitromicina
    • Corticóides
    • Anticoagulantes
    • ...
  • O que funciona DE FATO?
    • ​UTI + Ventilação Invasiva?
    • Tratamento precoce?
    • ...

O que fazer?

No caso da COVID-19...

E se for algo "conhecido"?

Filtros?

 

Sobre o curso

Ementa

A disciplina de bioestatística tem como objetivo capacitar os alunos a organizar e analisar os dados de uma determinada população e tirar conclusões de associações com bases nesses dados para que ele possa interpretar criticamente a literatura biomédica. Enfoca as medidas de tendência central e dispersão, noções de amostragem, testes de significância para medidas e proporções, correlação, regressão linear simples, medidas de morbimortalidade, padronização direta e indireta. Desenvolver o raciocínio lógico e auxiliar o processo decisório através dos cálculos estatísticos na interpretação de estudos translacionais na área de saúde.

 

Bibliografia

  • BUSSAB, W.O. & MORETTIN, P.A. Estatística básica. 4a ed., Atual Editora, S.P., 1993. DEVORE, J. L. Probabilidade e Estatística para Engenharia e Ciências. São Paulo: Pioneira Thomson Learning, 2006, 692p.

  • LARSON, Ron; FARBER, Betsy. Estatística aplicada. 2.ed. São Paulo: Pearson Pretice Hall, 2004. MEYER, P.L. Probabilidade, aplicações a estatística. Rio de Janeiro: ENCE/IBGE, 1984. MORETTIN, LUIZ GONZAGA . Estatística básica: probabilidade e inferência. São Paulo: Pearson, 2010.

  • ALMEIDA FILHO, N.; ROUQUAYROL, M. Z. Introdução à Epidemiologia. 4. ed. Rio de Janeiro: Guanabara Koogan, 2006.

  • ALTMAN, D. G. Practical Statistics for Medical Research. New York: Chapman & Hall, 1991.

  • HULLEY, S. B. et al. Delineando a Pesquisa Clínica: uma abordagem epidemiológica. 3. ed. Porto Alegre: Artmed, 2008.

  • JEWELL, N. P. Statistics for Epidemiology. New York: Chapman & Hall/CRC, 2004. RIFFENBURFH, R. H. Statistics in Medicine. 2. ed. San Diego: Elsevier Academic, 2006. ROSNER, B. Fundamentals of Biostatistics. 6. ed. Belmont: Duxbury, 2006.

Outras Sugestões

CALLEGARI-JACQUES, Sidia M. Bioestatística: princípios e aplicações. Porto Alegre: ARTMED,2004.
VIEIRA, Sônia. Introdução à bioestatística. 3. ed. Rio de Janeiro: Elsevier, 2004.
BERQUÓ, Elza Salvatore; SOUZA, José Maria Pacheco de; GOTLIEB, Sabina Lea Davidson. Bioestatística. 2. ed. Ver. São Paulo: EPU, 2003.
JEKEL, James F.; KATZ, David L.; ELMORE, Joam G. Epidemiologia, bioestatística e medicina
preventiva. Porto Alegre: ARTMED, 2005.
SOARES, José Francisco; SIQUEIRA, Arminda Lucia. Introdução a estatística médica. 2. ed. Belo
Horizonte: COOPMED, 2002.

Outros textos

Estatística: O que é, para que serve, como funciona
por Charles Wheelan
Link: http://a.co/d/5c21rcZ

The Model Thinker: What You Need to Know to Make Data Work for You (English Edition)
por Scott E. Page
Link: http://a.co/d/gvY9mnf

Princípios de bioestatística
por Marcello Pagano
Link: http://a.co/d/7zi7NGy

Outros textos

Conceitos sobre significância estatística em Biociências
por Jean Faber
 

Estatística Prática para Cientistas de Dados

por Andrew Bruce
 

O que espero...

Photo by Kevin Ku from Pexels

Anyone can...

Photo by Kevin Ku from Pexels

No fundo, será uma PODEROSA "calculadora"...

Photo by Eduardo Rosas from Pexels

E um grande aliado nos processos decisórios...

Photo by rawpixel.com from Pexels

E , confiem, é BEM melhor do que fazer "na mão"...

Clique aqui!

Usando o R e outros...

Usando o R e outros...

Há inúmeras fontes GRATUITAS disponiveis... e outras pagas!

Recomendo o curso gratuito do módulo "Introduction to R"

Probabilidade Condicional

Suppose there are two bowls of cookies. Bowl 1contains 30 vanilla cookies and 10 chocolate cookies. Bowl 2 contains 20 of each. Now suppose you choose one of the bowls at random and, without looking, select a cookie at random.

\boxed{p(A|B) = \cfrac{p(A \cap B)}{p(B)}}

Cap. 1, Think Bayes, Allen Downey http://greenteapress.com/wp/think-bayes/

\begin{aligned} &a) \enspace p(Bowl\,1)\, =\, ?\\ &b) \enspace p(vanilla\,|\, Bowl\,1)\, =\, ?\\ &c) \enspace p(chocolate\,|\, Bowl\,2)\, =\, ?\\ &d) \enspace p(vanilla)\, =\, ?\\ &e) \enspace p(chocolate)\, =\, ? \end{aligned}

Probabilidade Condicional

Suppose there are two bowls of cookies. Bowl 1contains 30 vanilla cookies and 10 chocolate cookies. Bowl 2 contains 20 of each. Now suppose you choose one of the bowls at random and, without looking, select a cookie at random. The cookie is vanilla. What is the probability that it came from Bowl 1?

Cap. 1, Think Bayes, Allen Downey http://greenteapress.com/wp/think-bayes/

\boxed{ \def\arraystretch{1.5} \begin{array}{c:c:c} \, & V & C \\ \hline B1 & 30 & 10 \\ \hdashline B2 & 20 & 20 \end{array}}
\boxed{p(\text{Bowl\,1}\,|\,\text{vanilla})\, =\, \cfrac{p(\text{Bowl\,1}\, \cap \text{vanilla})}{p(\text{vanilla})}}

Área para solução de exercícios

Probabilidade Condicional

Suppose there are two bowls of cookies. Bowl 1contains 30 vanilla cookies and 10 chocolate cookies. Bowl 2 contains 20 of each. Now suppose you choose one of the bowls at random and, without looking, select a cookie at random. The cookie is vanilla. What is the probability that it came from Bowl 1?

Cap. 1, Think Bayes, Allen Downey http://greenteapress.com/wp/think-bayes/

PORTA DOS DESESPERADOS

Aplicações - Epidemiologia

  • Incidência - Razão entre a quantidade de novos casos da doença e a quantidade de pessoas expostas;

  • Prevalência - Quantidade de pessoas com a doença [condição] na população;

  • Taxa de Mortalidade - Proporção de pessoas que morreram por uma dada causa na população [em um período de tempo];

  • Letalidade - Proporção de pessoas que morreram por uma dada doença [causa] na população infectada [afetada pela causa];

Aplicações - Epidemiologia

  • Para determinar esses diversos índices, diferentes desenhos de estudo são possíveis. Caso tenham mais interesse no tema, procurem ler sobre:

    • Estudos Longitudinais

    • Estudos Transversais

    • Estudos de Coorte

    • Estudos Caso - Controle

    • Estudos de Prevalência

  • Sobre os índices da página anterior, reflitam sobre como seriam necessários estudos para inferir os parâmetros definidos lá.

A famosa COORTE...

Testes diagnósticos - Definições

  • Sensibilidade (S+) - Probabilidade de um teste dar positivo para uma amostra positiva;

  • Especificidade (S-) - Probabilidade de um teste dar negativo para uma amostra negativa;

  • Acurácia (AC) - Probabilidade de um teste classificar adequadamente uma amostra, isto é, classificar como positiva uma amostra positiva ou como negativa, caso contrário;

  • Taxa de Falsos Negativos (FNR) - Probabilidade de um teste dar negativo para uma amostra positiva;

  • Taxa de Falsos Positivos (FPR) - Probabilidade de um teste dar positivo para uma amostra negativa;

Testes diagnósticos - Definições

  • Valor Preditivo Positivo (PPR) - Probabilidade de uma amostra ser positiva dado o resultado do teste é positivo;

  • Valor Preditivo Negativo (NPR) - Probabilidade de uma amostra ser negativa dado o resultado do teste é negativo;

\begin{aligned} p(P|T^{+})=\cfrac{p(P \cap T^{+})}{p(T^{+})}=\cfrac{p(P \cap T^{+})}{p(T^{+}|P)p(P)+p(T^{+}|N)p(N)}\\ p(P|T^{+})=\cfrac{S^{+}p(P)}{S^{+}p(P)+(1-S^{-})(1-p(P))}\\ \end{aligned}

Testes diagnósticos

\boxed{ \def\arraystretch{1.5} \begin{array}{c:c:c} \, & P & N \\ \hline T^{+}\,[P] & VP & FP \\ T^{-}\,[N] & FN & VN \end{array}}

Padrão-Ouro

Teste

\begin{aligned} \boxed{S^{+}=p(T^{+}|P)=\cfrac{VP}{VP+FN}}& \\ \boxed{S^{-}=p(T^{-}|N)=\cfrac{VN}{VN+FP}}& \\ \boxed{A_{c}=p(T^{+}|P)p(P)+p(T^{-}|N)p(N)}& \\ \boxed{FPR\,=p(T^{+}|N)=\cfrac{FP}{FP+VN}}& \\ \boxed{FNR\,=p(T^{-}|P)=\cfrac{FN}{VP+FN}}& \\ \end{aligned}
\bold{\text{Legenda:} \enspace} \begin{aligned} &P:\, Positivo\\ &N:\, Negativo\\ &T^{+}:\, Teste Positivo\\ &T^{-}:\, Teste Negativo\\ \end{aligned}

Testes diagnósticos

\boxed{ \def\arraystretch{1.5} \begin{array}{c:c:c} \, & P & N \\ \hline T^{+}\,[P] & VP & FP \\ T^{-}\,[N] & FN & VN \end{array}}

Padrão-Ouro

Teste

\begin{aligned} \boxed{S^{+}=p(T^{+}|P)=\cfrac{VP}{VP+FN}}& \\ \boxed{S^{-}=p(T^{-}|N)=\cfrac{VN}{VN+FP}}& \\ \boxed{A_{c}=p(T^{+}|P)p(P)+p(T^{-}|N)p(N)}& \\ \boxed{FPR\,=p(T^{+}|N)=\cfrac{FP}{FP+VN}}& \\ \boxed{FNR\,=p(T^{-}|P)=\cfrac{FN}{VP+FN}}& \\ \end{aligned}
\bold{\text{Legenda:} \enspace} \begin{aligned} &P:\, Positivo\\ &N:\, Negativo\\ &T^{+}:\, Teste Positivo\\ &T^{-}:\, Teste Negativo\\ \end{aligned}

Testes diagnósticos

Aplicações - Epidemiologia

  • Risco Relativo - Razão entre a probabilidade do grupo que tem o fator de risco desenvolver a condição-alvo e a probabilidade do grupo que não tem o fator de risco desenvolver a condição-alvo;

\begin{aligned} &RR=\cfrac{p(P|\text{Exposto})}{p(P|\text{Não\,Exposto})}=\cfrac{I_{E}}{I_{\bar{E}}}=\cfrac{I_{\text{Exposto}}}{I_{\text{Não\,Exposto}}}\\ \end{aligned}

  • Utilidade: Identificação de fatores de risco [RR > 1] ou fatores protetores [RR < 1] em relação a condição em estudo. Muito utilizado na área cardiovascular, sendo muitos resultados obtidos do Framingham Heart Study [70 ANOS!!!]

Razão de Verossimilhança

  • Definição: razão entre a probabilidades de um evento acontecer em uma população portadora da doença e a probabilidade dele acontecer numa população não portadora;

\begin{aligned} &RV^{+}=\cfrac{p(T^{+}|P)}{p(T^{+}|N)}=\cfrac{S^{+}}{1-S^{-}} \\ &RV^{-}=\cfrac{p(T^{-}|P)}{p(T^{-}|N)}=\cfrac{1-S^{+}}{S^{-}} \\ \end{aligned}

Razão de Chances - Odds Ratio (OR)

  • Nem sempre é possível estimar a incidência de uma dada doença num grupo a partir do desenho do mesmo. Entretanto, é possível fazer uma estimativa em função das chances de uma determinada condição ser desenvolvida nos diferentes grupos da amostra, caso e controle.

\def\arraystretch{1.5} \begin{array}{c:c:c} Grupo & P & N \\ \hline Caso\, & a & b \\ Ctrl\, & c & d \\ \end{array} \\
\begin{aligned} &RV^{+}=\cfrac{p(P|\text{Caso})}{p(P|\text{Ctrl})}=\cfrac{\frac{a}{a+b}}{\frac{c}{c+d}}=\cfrac{a(c+d)}{c(a+b)}\\ &RV^{-}=\cfrac{p(N|\text{Caso})}{p(N|\text{Ctrl})}=\cfrac{\frac{b}{a+b}}{\frac{d}{c+d}}=\cfrac{b(c+d)}{d(a+b)}\\ &OR= \cfrac{RV^{+}}{RV^{-}}=\cfrac{ad}{bc}\\ \end{aligned}

Distribuição Binomial (Bernoulli)

Premissas:

  1. Número fixo de ensaios (n), cada um resulta em dois resultados mutuamente exclusivos;
  2. Os resultados dos n ensaios são independentes;
  3. A probabilidade de sucesso (p) para cada ensaio é constante;
P(X=x)=\dbinom{n}{x}p^{x}(1-p)^{n-x},\,\text{onde:\,}\dbinom{n}{x}=\cfrac{n!}{x!(n-x)!}

Distribuição Binomial (Bernoulli)

Exemplo 1: Uma moeda não viciada é utilizada num jogo de cara e coroa "sofisticado" composto por múltiplos lançamentos. Suponha que a moeda seja lançada n vezes em sequência.

a. Seja n = 3. Qual é a probabilidade do número de caras ser igual a zero? Igual a 1? Igual a 2? Igual a 3?

b. Seja n=10. Qual é a probabilidade do número de caras ser igual ao de coroas? E maior? E menor?

c. O que acontece com os casos anteriores se a moeda for trocada por uma moeda cuja probabilidade de cara for igual a 0,7?

P(X=x)=\dbinom{n}{p}p^{x}(1-p)^{n-x},\,\text{onde:\,}\dbinom{n}{p}=\cfrac{n!}{p!(n-p)!}

Distribuição Binomial (Bernoulli)

Exemplo 1: Uma moeda não viciada é utilizada num jogo de cara e coroa "sofisticado" composto por múltiplos lançamentos. Suponha que a moeda seja lançada n vezes em sequência.

a. Seja n = 3. Qual é a probabilidade do número de caras ser igual a zero? Igual a 1? Igual a 2? Igual a 3?

b. Seja n=10. Qual é a probabilidade do número de caras ser igual ao de coroas? E maior? E menor?

c. O que acontece com os casos anteriores se a moeda for trocada por uma moeda cuja probabilidade de cara for igual a 0,7?

P(X=x)=\dbinom{n}{p}p^{x}(1-p)^{n-x},\,\text{onde:\,}\dbinom{n}{p}=\cfrac{n!}{p!(n-p)!}

Observação [Binômio de Newton]

(a+b)^n=\sum\limits_{k=0}^n \dbinom{n}{p}a^{k}\,b^{n-k}
[p+(1-p)]^n=\sum\limits_{k=0}^n \dbinom{n}{p}p^{k}\,(1-p)^{n-k}=\sum\limits_{k=0}^n P(X=k)
\sum\limits_{k=0}^n P(X=k) = (p+1-p)^{n}=1^{n}=1