The Chambolle—Pock method
1. Background
We want to solve problems of the form
\[\min_{x\in\R^n}\max_{y\in\R^m}L(x,y),\]
where \(L\) is a convex-concave function.
\(L\) will always assume the form
\[L(x,y)=\phi(x,y)+f(x)-g(y),\]
for \(f\) convex, \(g\) concave and \(\phi\) smooth convex-concave.
Where do min-max problems come from?
1. Optimization under constraints
\[\min_{x :\, h(x)=0}f(x)=\min_x\max_{y} f(x)+y^\top\!h(x)\]
More generally, sum of two convex functions,
\[\min_{x}f_1(x)+f_2(Ax)=\min_x\max_{y} f_1(x)+y^\top\!Ax-f_2^*(y)\]
Where do min-max problems come from?
2. Game theory: two-player zero-sum games.
Player 1 can choose strategy \(x\in\R^n\).
Player 2 can choose strategy \(y\in\R^m\).
Payoff of player 2 : \(L(x,y)\).
Payoff of player 1 : \(-L(x,y)\).
A Nash equilibrium is a pair \((x^*,y^*)\) such that
\[-L(x^*,y^*) \ge -L(x,y^*)\quad\text{for all } x,\]
and
\[L(x^*,y^*) \ge L(x^*,y)\quad\text{for all } y \]
i.e. a saddle-point of \(L\):
\[L(x^*,y)\le L(x^*,y^*)\le L(x,y^*).\]
Where do min-max problems come from?
Prop If
\[L(x^*,y)-L(x,y^*)\le 0\]
for all \(x,y\), then \((x^*,y^*)\) is a saddle-point
Proof
(i) Choose \(x=x^*\), then
\[L(x^*,y)\le L(x^*,y^*).\]
(ii) Choose \(y=y^*\), then
\[L(x^*,y^*)\le L(x,y^*).\]
Proof \(\min\max\) is always \(\ge\max\min\). So just need to show
\[\min_x\max_yL(x,y)\le\max_y\min_xL(x,y)\]
We have
\[\min_x\max_yL(x,y)\le\max_yL(x^*,y)\]
and the saddle-point identity guarantees that
\[\max_yL(x^*,y)\le L(x^*,y^*).\]
Similarly, \(\max_y\min_xL(x,y)\ge \min_xL(x,y^*),\) and the saddle-point identity gives us
\[\min_xL(x,y^*)\ge L(x^*,y^*).\]
Prop If \(x^*,y^*\) is a saddle-point of \(L\) then
\[\min_x\max_y L(x,y)=\max_y\min_x L(x,y)\]
En bref
The important object is the gap function
\[G_{\bar x,\bar y}(x,y):=L(\bar x,y)-L(x,\bar y).\]
1. \((x^*,y^*)\) is a saddle-point of \(L\) iff
\[G_{x^*,y^*}(x,y) \le 0\]
for all \((x,y)\) .
2. Therefore \(G_{x_n,y_n}(x,y)\) will be used to quantity how good an approximate saddle \((x_n,y_n)\) point is.
2. The Chambolle—Pock scheme
Here \(\sigma>0\) and \(\tau>0\) are step-sizes.
\[\tilde y_{n+1}=2y_n-y_{n-1},\]
\[x_{n+1}=\argmin_xL(x,\tilde y_{n+1})+\frac{1}{2\sigma}\|x-x_n\|^2,\]
\[y_{n+1}=\argmax_yL(x_{n+1},y)-\frac{1}{2\tau}\|y-y_n\|^2.\]
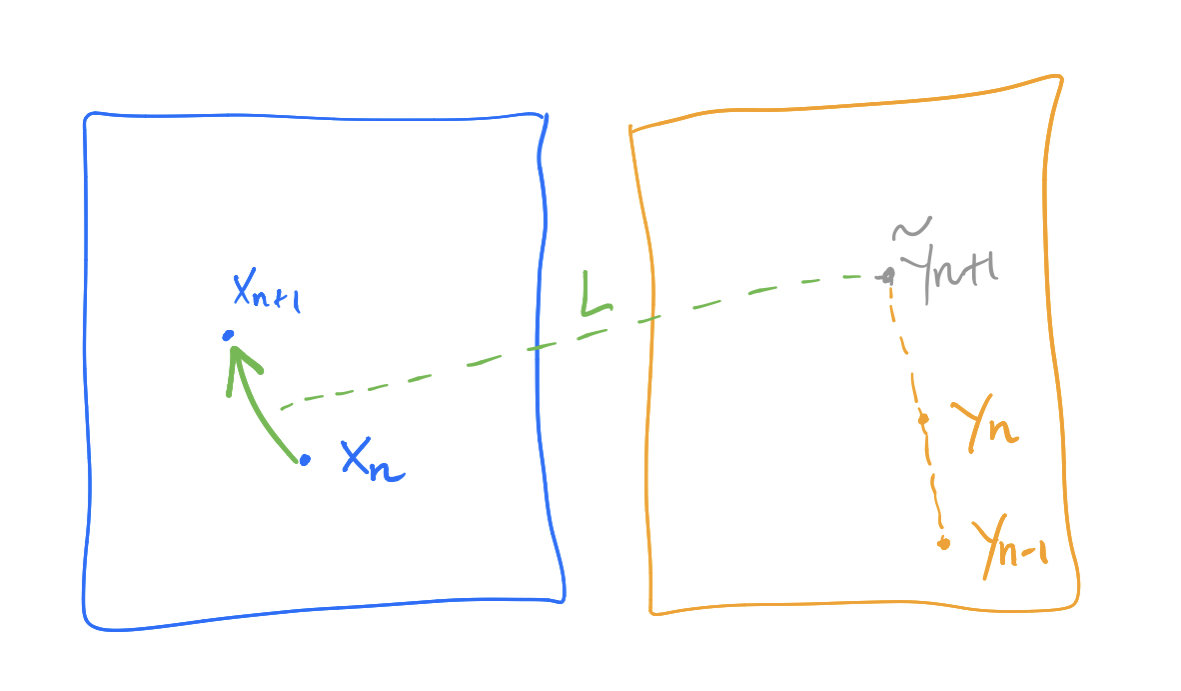
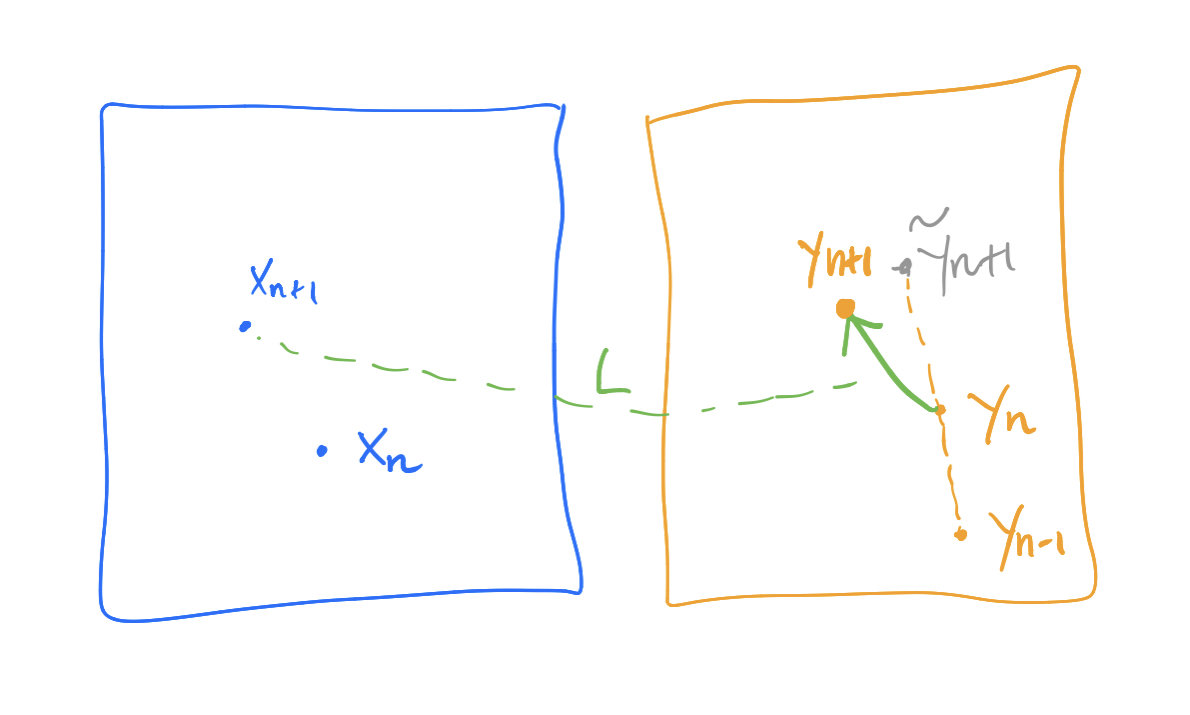
Reference: Chambolle, Antonin, and Thomas Pock. "On the ergodic convergence rates of a first-order primal–dual algorithm." Mathematical Programming 159.1-2 (2016): 253-287.
In practice, \(L(x,y)=f(x)+x^\top\!Ay-g(y)\).
The \(x\)-update is
\[x_{n+1}=\argmin_xf(x)+x^\top\!A\tilde{y}_{n+1}+\frac{1}{2\sigma}\|x-x_n\|^2,\]
i.e. a proximal step on \(f(x)+x^\top\!A\tilde{y}_{n+1}\).
If \(f\) is smooth, also possible to do an explicit step
\[x_{n+1}=x_n-\sigma\nabla f(x_n)-\sigma A\tilde{y}_{n+1}\]
Role of the extrapolation \(\tilde{y}\)
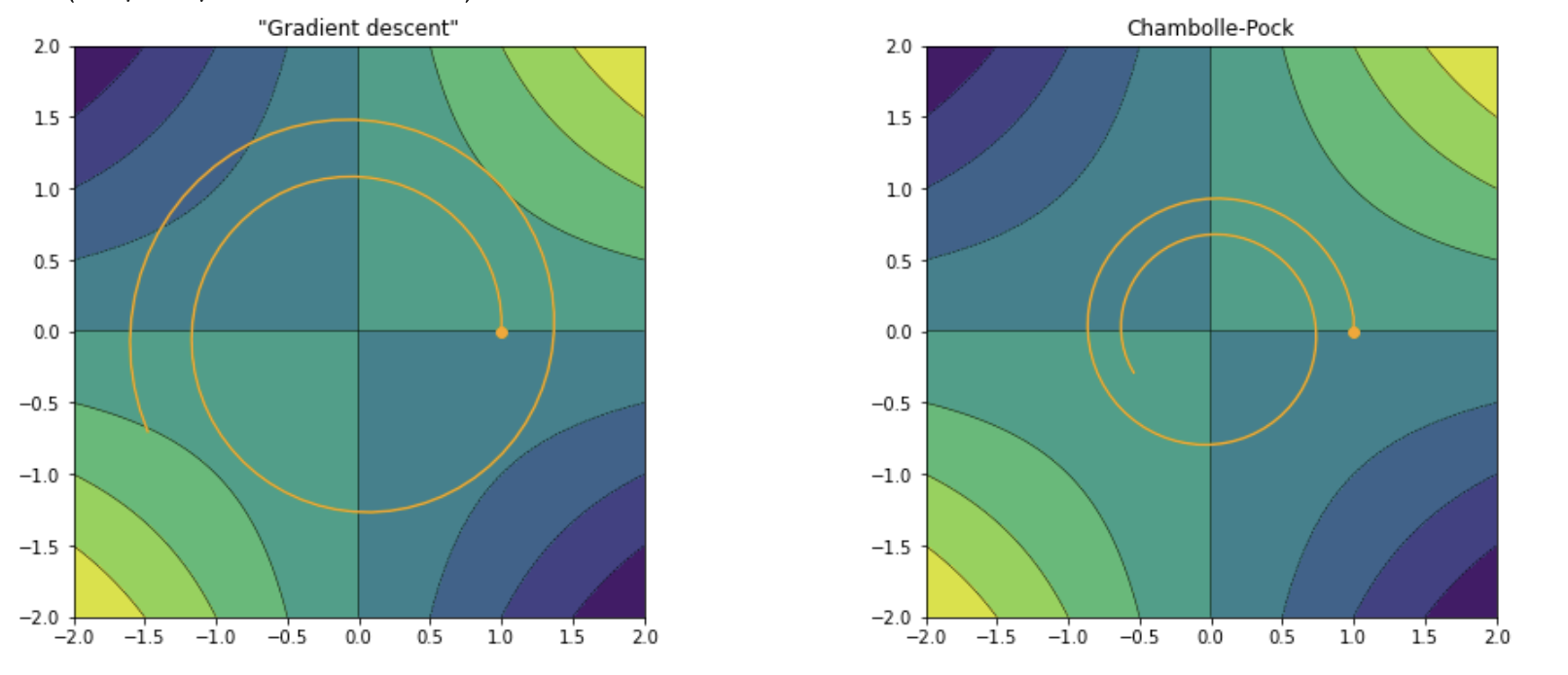
"Gradient descent"
Chambolle–Pock
Most simple example: \(L(x,y)=xy\) in 1d

Thm Let \(L(x,y)=f(x)-g(y)+x^\top\!Ay\). If the stepsizes are such that
\[\sigma\tau\|A\|^2\le 1,\]
then
\[L(X_n,y)-L(x,Y_n)\le\frac 1 n \Big(\frac{\|x-x_0\|^2}{2\sigma}+\frac{\|y-y_0\|^2}{2\tau}\Big)\]
Here \(X_n=\frac 1 n\sum_{k=1}^nx_k\) and \(Y_n=\frac 1 n\sum_{k=1}^ny_k\).
Application : \(L^1\) optimal transport
EMD problem:
\[\min_{m} \int_{\Omega}|m(x)|\,dx\]
over vector fields \(m\colon\Omega\to\R^d\) such that
\[-\mathrm{div}(m)=f\quad\text{in } \Omega\]
and \(m\cdot n=0\) on \(\partial\Omega\).
Optimal transport : \(f=\nu-\mu\).
Reference: Jacobs, M., Léger, F., Li, W., & Osher, S. (2019). Solving large-scale optimization problems with a convergence rate independent of grid size. SIAM Journal on Numerical Analysis, 57(3), 1100-1123.
Application : \(L^1\) optimal transport
EMD problem:
\[\min_{-\mathrm{div}(m)=f} \int_{\Omega}|m|\]
Min-max formulation:
\[\min_{-\mathrm{div}(m)=f}\max_{p}\int_{\Omega}m(x)\cdot p(x)\,dx-\|p\|_{\infty}\]
Set
\[L(m,p)=F(m)+\langle m,p\rangle-\|p\|_\infty,\]
Application: matrix games
Two players zero-sum game.
Player 1 can choose strategy \(i=1\dots n\),
player 2 can choose strategy \(j=1\dots m\).
Denote \(a_{ij}\) be the payoff of player 2.
The Nash equilibrium will be given by
\[\min_{p\in\Delta_n}\max_{q\in\Delta_m} p^\top\!Aq.\]
Here \(\Delta_n=\{p\in\R^n : p_i\ge 0,\sum_ip_i=1\}\)