Gradient descent with a general cost
Flavien Léger
joint work with Pierre-Cyril Aubin-Frankowski

1. A new class of algorithms
2. Alternating minimization
3. Applications
Outline
\[x_{n+1}=x_n-\frac{1}{L}\nabla f(x_n)\]
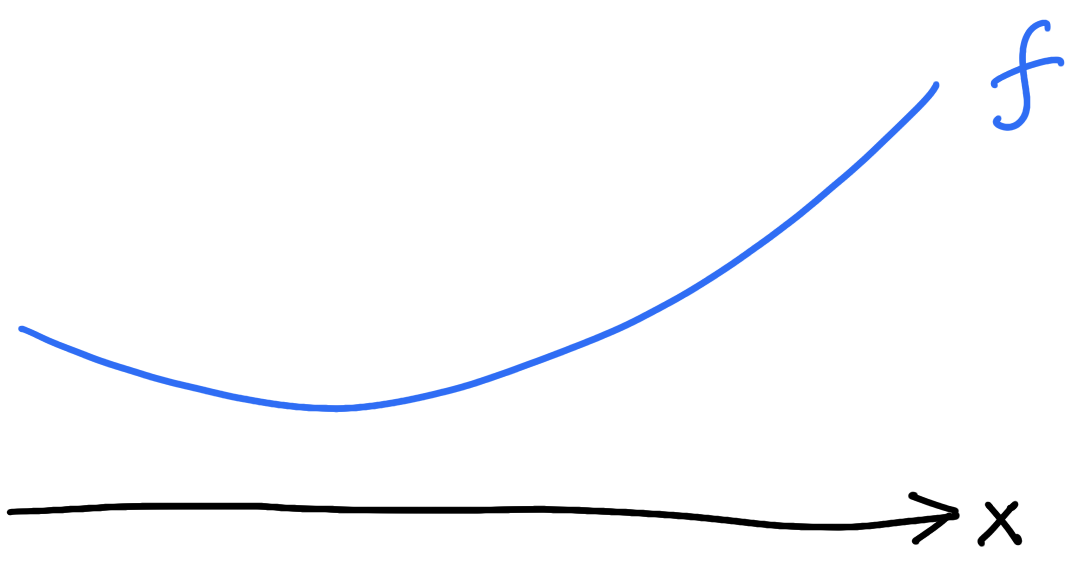
Objective function \(f\colon \mathbb{R}^d\to\mathbb{R}\)
Vanilla gradient descent
\(f\) is \(L\)-smooth if \[\nabla^2f\leq L I_{d\times d}\]
1. A new class of algorithms
D E F I N I T I O N
Minimizing movement point of view
Two steps:
1) majorize: find the tangent parabola (“surrogate”)
2) minimize: minimize the surrogate
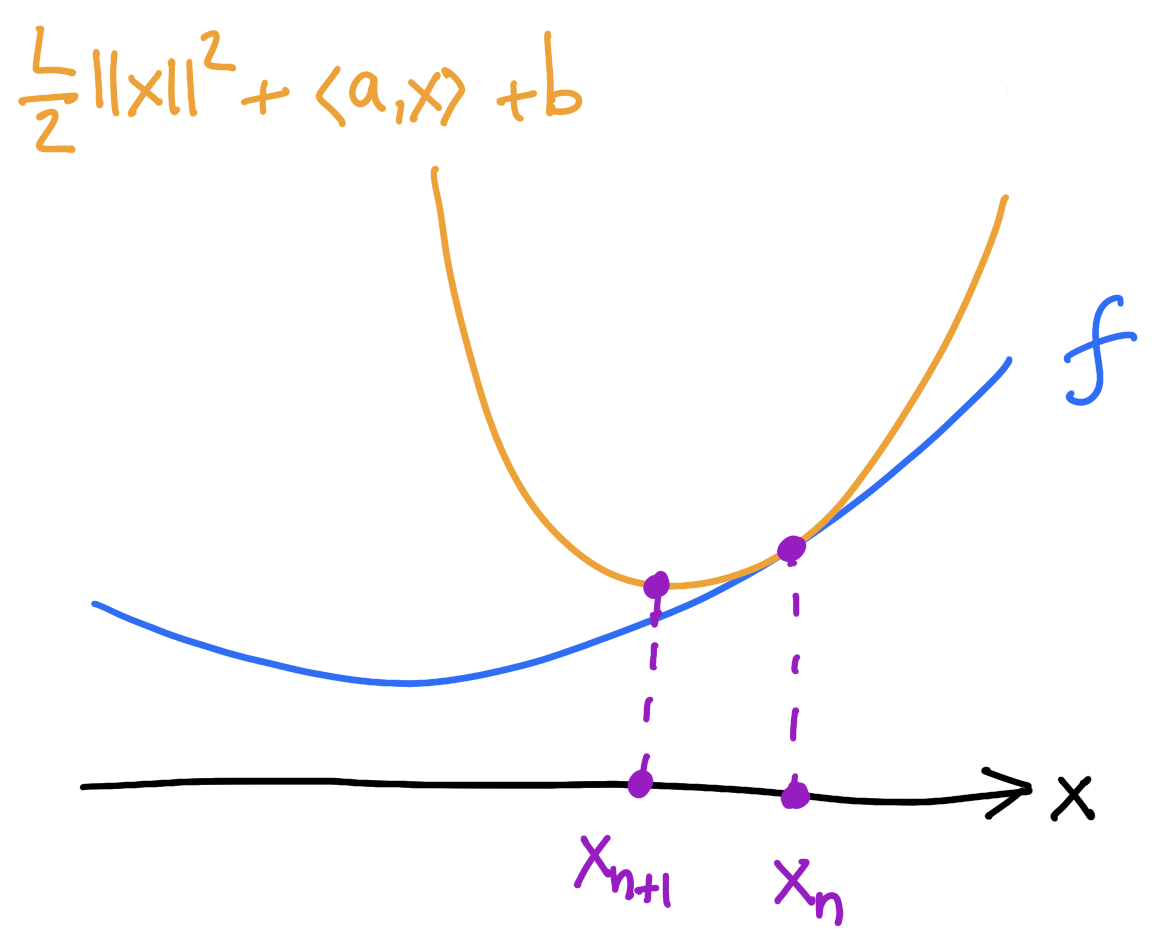
Take \(f\) to be \(L\)-smooth
The \(y\)-step
The \(y\)-step (“majorize”) is:
\[y_{n+1} = \argmin_{y}\phi(x_n,y)\]
The \(x\)-step (”minimize”) is:
\[x_{n+1} = \argmin_{x}\phi(x,y_{n+1})\]

Family of majorizing functions \(\phi(x,y)\)
\(\phi(\cdot,y_{n+1})\)
Optimal transport tools
The \(c\)-transform of \(f\) is
\[f^c(y)=\inf\{\lambda\in\mathbb{R} : \forall x\in\mathbb{R}^d, \,f(x)\le c(x,y)+\lambda\}\]
Given: \(X\) and \(f\colon X\to\mathbb{R}\)
Choose: \(Y\) and \(c(x,y)\)
\(c(\cdot,y)+f^c(y)\)
\(c(\cdot,y)+\lambda\)
D E F I N I T I O N
\(\frac{L}{2}\lVert x-y\rVert^2\)
\(c(x,y)\).
\[f(x)\leq c(x,y)+f^c(y)\]
Optimal transport tools
\(f\) is \(c\)-concave if
\[f(x)=\inf_{y\in Y}c(x,y)+f^c(y)\]
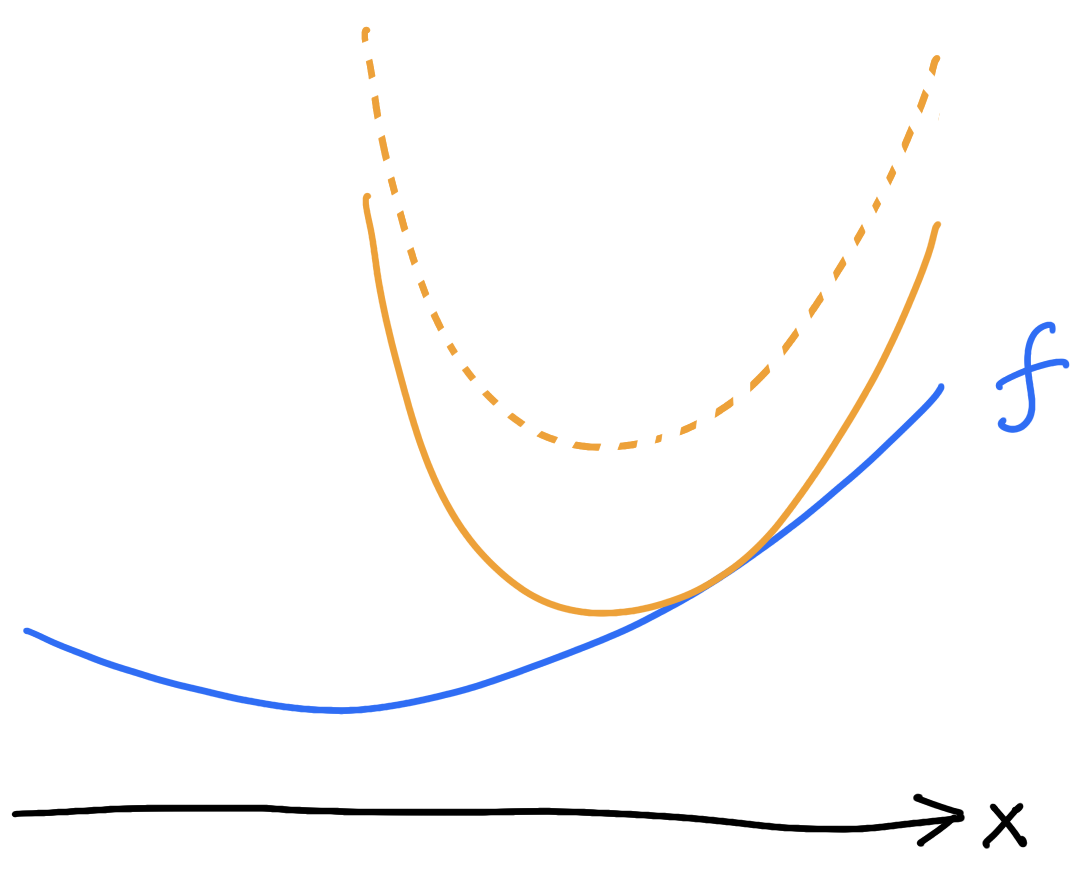
Envelope of the surrogates
Can always find a tangent upperbound
Interpreted as a generalized smoothness condition
D E F I N I T I O N

\[\inf_{x\in X} f(x)=\inf_{x\in X}\inf_{y\in Y} c(x,y)+f^c(y)=\phi(x,y)\]
\[f(x)\leq c(x,y)+f^c(y)\eqqcolon\phi(x,y)\]
Gradient descent with a general cost
If \(f\) is \(c\)-concave (i.e. \(f(x)=\inf_{y} c(x,y)+f^c(y)\)):

\(\phi(\cdot,y_{n+1})\)
Examples
\(c(x,y)=u(x)-u(y)-\langle\nabla u(y),x-y\rangle\): mirror descent
\[\nabla u(x_{n+1})-\nabla u(x_n)=-\nabla f(x_n)\]
\(c(x,y)=u(y|x)\): natural gradient descent
\[x_{n+1}-x_n=-\nabla^2 u(x_n)^{-1}\nabla f(x_n)\]
\(c(x,y)=\frac{L}{2}d_M^2(x,y)\): Riemannian gradient descent
\[x_{n+1}=\exp_{x_n}(-\frac{1}{L}\nabla f(x_n))\]
Newton
\(-\nabla_xc(x,y)=\xi\Leftrightarrow y=\exp_x(\frac{1}{L}\xi)\)
\(u(x|y)\)
2. Alternating minimization
\(\phi(x,y)=c(x,y)+f^c(y)\) : previous algo
\(\phi(x,y)=c(x,y)+f^c(y)+g(x)\) : forward–backward version
\(X,Y\)
\(\phi\colon X\times Y\to\mathbb{R}\) , \(\mathrm{minimize}_{x\in X,y\in Y} \;\phi(x,y)\)
Setup
The five-point property
For all \(x,y,y_n\),
\[\phi(x,y_{n+1})+\phi(x_n,y_n)\leq \phi(x,y)+\phi(x,y_n)\]
They show: \(\phi(x_n,y_n)\to\inf \phi\)
No structure beyond \((X,Y,\phi)\)
Csiszár–Tusnády (’84):
(FPP)
If \(\phi\) satisfies the FPP then
\[\phi(x_n,y_n)\leq \phi(x,y)+\frac{\phi(x,y_0)-\phi(x_0,y_0)}{n}\]
Rem: strong FPP gives linear rate
T H E O R E M
The five-point property
Limitation: FPP is nonlocal
The Kim–McCann metric and cross-curvature
Kim–McCann metric: \(-\nabla^2_{xy}c(x,y)(\xi,\eta)\)
\[\phi(x,y)=c(x,y)+g(x)+h(y)\]
Cross-curvature: \(\mathfrak{S}_c=-\nabla^4_{xyxy}c + \nabla^3_{xxy}c\,(\nabla^2_{xy}c)^{-1}\nabla^3_{xyy}c\)
\(\delta_c(x',y';x,y)=c(x,y')+c(x',y)-c(x,y)-c(x',y')\)
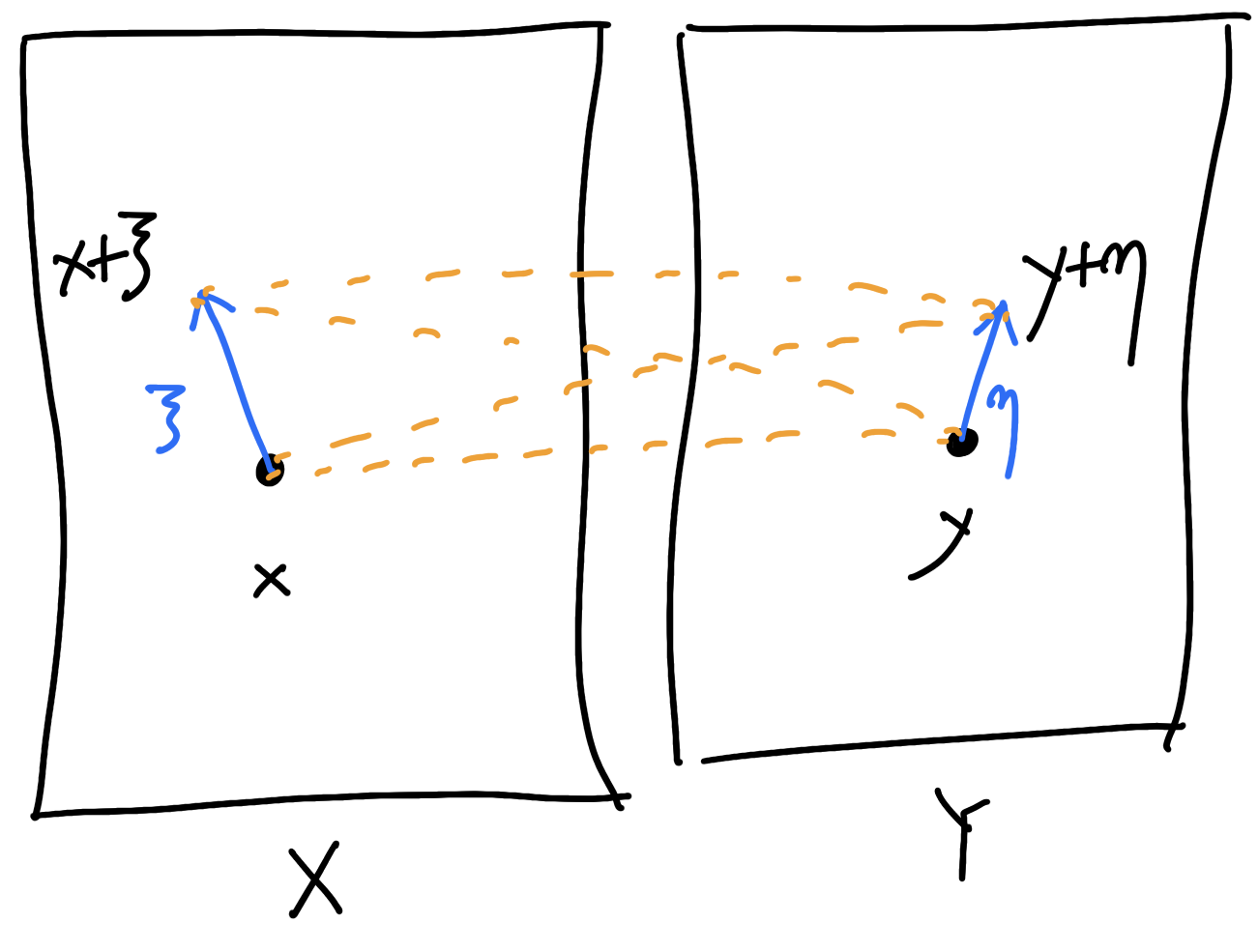
Kim–McCann ’10
(Ma–Trudinger–Wang ’05)
A local criteria for the five-point property
Suppose that \(\phi\) (i.e. \(c\)) has nonnegative cross-curvature.
If \(F(x)\coloneqq\inf_{y\in Y}\phi(x,y)\) is convex on every Kim–McCann geodesic \(t\mapsto (x(t),y)\) satisfying \(\nabla_x\phi(x(0),y)=0\), then \(\phi\) satisfies the FPP.
T H E O R E M
\[\phi(x,y)=c(x,y)+g(x)+h(y)\]
3. Applications
Gradient descent and mirror descent
\(c(x,y)=u(x|y)\longrightarrow\) mirror descent
\[\nabla u(x_{n+1})-\nabla u(x_n)=-\nabla f(x_n)\]
\(c\)-concavity \(\longrightarrow\) relative smoothness \(\nabla^2f\leq\nabla^2u\)
FFP \(\longrightarrow\) convexity \(\nabla^2 f\geq 0\)
Convergence rate: if \(0\leq \nabla^2f\leq \nabla^2u\) then
\[f(x_n)\leq f(x)+\frac{u(x|x_0)}{n}\]
Natural gradient descent and Newton's method
\(c(x,y)=u(y|x)\longrightarrow\) NGD
\[x_{n+1}-x_n=-\nabla^2u(x_n)^{-1}\nabla f(x_n)\]
Convergence rate: if \[\nabla^3u(\nabla^2u^{-1}\nabla f,-,-)\leq \nabla^2f\leq \nabla^2u+\nabla^3u(\nabla^2u^{-1}\nabla f,-,-)\] then
\[f(x_n)\leq f(x)+\frac{u(x_0|x)}{n}\]
Newton's method: new global convergence rate.
New condition on \(f\) similar but different from self-concordance
T H E O R E M
Riemannian setting
\((M,g),\quad X=Y=M,\quad c(x,y)=\frac{L}{2} d^2(x,y)\)
1. Explicit: \(x_{n+1}=\exp_{x_n}\big(-\frac{1}{L}\nabla f(x_n)\big)\)
\(R\geq 0\): (smoothness and) \(\nabla^2f\geq 0\) gives \(O(1/n)\) convergence rates
\(R\leq 0\): ? (nonlocal condition)
2. Implicit: \(x_{n+1}=\argmin_{x} f(x)+\frac{L}{2}d^2(x,x_n)\)
\(R\leq 0\): \(\nabla^2f\geq 0\) gives \(O(1/n)\) convergence rates
\(R\geq 0\): if nonnegative cross-curvature then convexity of \(f\) on Kim–McCann geodesics saves the day
da Cruz Neto, de Lima, Oliveira ’98
Bento, Ferreira, Melo ’17
See: Ambrosio, Gigli, Savaré ’05
Bregman alternating minimization
\(\phi(x,y)=u(x|y)+g(x)+h(y)\)
If \(g=0\) : mirror descent on \(f(x)\coloneqq \inf_yc(x,y)+h(y)\)
- \(u=\frac{L}{2}\lVert\cdot\rVert^2\) : POCS, (forward–backward) gradient descent
- \(u=\mathrm{KL}\) : EM algorithm, Sinkhorn
Proposition: if \(f+g\) is convex then \(O(1/n)\) convergence rate.
If \(f+g\) is strongly convex then linear rate.