An intrinsic geometry for alternating minimization

Flavien Léger

joint work with Pierre-Cyril Aubin-Frankowski

1. Alternating minimization

2. The Kim–McCann geometry

3. Applications

Outline

\begin{aligned} y_{n+1} &= \argmin_{y\in Y} \phi(x_n,y)\\ x_{n+1} &= \argmin_{x\in X} \phi(x,y_{n+1}) \end{aligned}

For each \(x\in X\): \(y\mapsto \phi(x,y)\) has a unique minimizer.

For each \(y\in Y\): \(x\mapsto \phi(x,y)\) has a unique minimizer.

Alternating minimization

\[\operatorname*{minimize}_{x\in X,\,y\in Y} \;\phi(x,y)\]

A L G O R I T H M

\(X,Y\) two sets,

\(\phi\colon X\times Y\to\mathbb{R}\)

Assumptions:

Convergence rates: typically Euclidean space, \(\phi\) convex and \(L\)-smooth

(Beck–Tetruashvili ’13, Beck ’15)

Motivations

Expectation–Maximization in statistics

Sinkhorn (aka RAS, IPFP) for matrix scaling and optimal transport

Projection Onto Convex Sets

\min_{\theta,\pi}\operatorname{KL}(\pi|p_\theta)=:\Phi(\theta,\pi)

\pi\in\Pi(\mu,*),

\theta\in\Theta

model \(p_\theta\)

\(X,Y\): two convex subsets of \(\mathbb{R}^d\)

\min_{x\in X,\,y\in Y}\lVert x-y\rVert^2

Motivations 2: “Gradient descent” family

\[F(x)=\inf_{y\in Y} \phi(x,y)\]

\(X,Y\) two smooth manifolds

x_{n+1} = \displaystyle\argmin_{x\in X} \phi(x,y_{n+1}) \quad\longrightarrow \quad \nabla_x\phi(x_{n+1},y_{n+1})=0

y_{n+1} = \displaystyle\argmin_{y\in Y} \phi(x_n,y) \quad\longrightarrow\quad \nabla_x\phi(x_n,y_{n+1})=\nabla F(x_n)

\phi(x,y)=\frac{1}{2\tau}\lVert x-y\rVert^2 + h(y)\quad\rightsquigarrow\qquad x_{n+1}-x_n=-\tau\nabla F(x_n), \qquad y_n=x_n

\phi(x,y)=\underbrace{u(x|y)} + h(y)\quad\rightsquigarrow\qquad \nabla u(x_{n+1})-\nabla u(x_n)=-\nabla F(x_n), \qquad y_n=x_n

= u(x)-u(y)-\langle\nabla u(y),x-y\rangle

\phi(x,y)=u(y|x) + h(y)\quad\rightsquigarrow\qquad x_{n+1}-x_n=-\nabla^2 u(x_n)^{-1}\nabla F(x_n), \qquad y_n=x_n

\phi(x,y)=\frac{1}{2\tau}d_M^2(x,y)+h(y)\quad\rightsquigarrow\qquad x_{n+1}=\exp_{x_n}(-\tau\nabla F(x_n)), \qquad y_n=x_n

Let \(\lambda\geq 0\). \(\phi\) has the \(\lambda\)-strong FPP if

\[\phi(x,y_{1})+(1-\lambda)\phi(x_0,y_0)\leq \phi(x,y)+(1-\lambda)\phi(x,y_0)\]

(\(\lambda\)-FPP)

D E F I N I T I O N

The five-point property

(\forall y_0)(\exists \,x_0,y_1)(\forall x,y)

x_{0} = \displaystyle\argmin_{x\in X} \phi(x,y_{0})

y_{1} = \displaystyle\argmin_{y\in Y} \phi(x_0,y)

inspired by Csiszár–Tusnády ’84

Characterizes (AM):

Intrinsic, no regularity on \(X,Y,\phi,\mathbb{R}\)

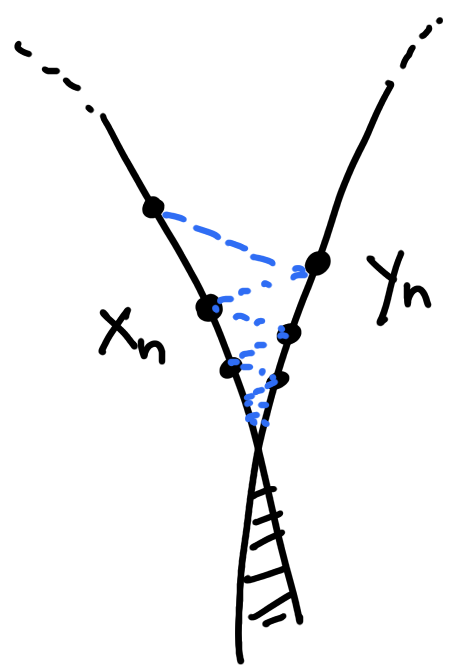
If \(\phi\) satisfies the FPP then

\[\phi(x_n,y_n)\leq \phi(x,y)+\frac{\phi(x,y_0)-\phi(x_0,y_0)}{n}\]

If \(\phi\) satisfies the \(\lambda\)-FPP then

\[\phi(x_n,y_n)\leq \phi(x,y)+\frac{\lambda[\phi(x,y_0)-\phi(x_0,y_0)]}{\Lambda^n-1},\]

where \(\Lambda\coloneqq(1-\lambda)^{-1}>1\).

T H E O R E M (FL–PCAF '23)

Convergence rates

Proof.

(FPP) \(\iff\)

\[\phi(x_{n+1},y_{n+1}) \leq \phi(x,y) + [\phi(x,y_n)-\phi(x_n,y_n)] - [\phi(x,y_{n+1})-\phi(x_{n+1},y_{n+1})]\]

Sum from \(0\) to \(n-1\) implies

\[n\,\phi(x_n,y_n) \leq n\,\phi(x,y) + [\phi(x,y_0)-\phi(x_0,y_0)] - [\phi(x,y_{n})-\phi(x_{n},y_{n})]\]

🤔

\[\phi(x_0,y_0)\leq \phi(x,y)+\phi(x,y_0)-\phi(x,y_{1})\]

(\forall y_0)(\exists \,x_0,y_1)(\forall x,y)

Transition to geometry

How to obtain the FPP

Answer: when \(X,Y\) smooth manifolds, find a path \((x(t),y(t))\) joining \((x_0,y_1)\) to \((x,y)\) such that

\(b(t)=\phi(x(t),y(t))+\phi(x(t),y_0)-\phi(x(t),y_{1})\) is convex.

Why: special structure of the FPP

(FPP) \(\iff b(0)\leq b(1)\)

and \(b'(0)=0\)

1. Alternating minimization

2. The Kim–McCann geometry

3. Applications

Pseudo-Riemannian metric on \(X\times Y\)

(Kim–McCann ’10)

D E F I N I T I O N : The Kim–McCann metric

\[g_{\scriptscriptstyle\text{KM}}=\frac12\begin{pmatrix}0 & -\nabla^2_{xy}c(x,y)\\-\nabla^2_{xy}c(x,y) & 0\end{pmatrix}\]

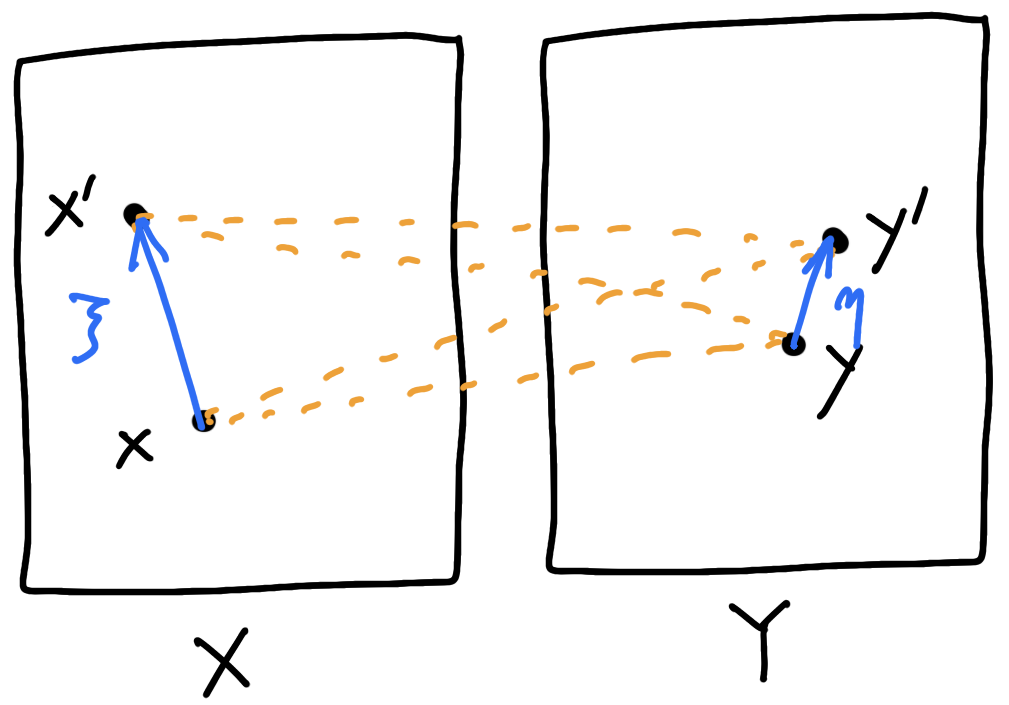
\(\delta_c(x+\xi,y+\eta;x,y)=\underbrace{-\nabla^2_{xy}c(x,y)(\xi,\eta)}_{\text{Kim--McCann metric ('10)}}+o(\lvert\xi\rvert^2+\lvert\eta\rvert^2)\)

\(\delta_c(x',y';x,y)=\)

\([c(x,y')+c(x',y)]-[c(x,y)+c(x',y')]\)

\(X, Y\): \(d\)-dimensional smooth manifolds

\(c\in C^4(X\times Y)\)

➡ \(c\)-segments: Kim–McCann geodesics \((x(t),y)\)

➡ cross-curvature: curvature of the Kim–McCann metric (aka MTW tensor)

T H E O R E M (Kim–McCann '11)

Under some assumptions on \((X,Y,c)\),

nonnegative cross-curvature \(\iff t\mapsto c(x(t),y)-c(x(t),y')\) is convex for any \(c\)-segment \((x(t),y)\).

\(c\)-segments and cross-curvature

A local criteria for the five-point property

Suppose that \(c\) has nonnegative cross-curvature.

T H E O R E M (FL–PCAF '23)

\(X, Y\): \(d\)-dimensional smooth manifolds

\(c\in C^4(X\times Y), \,\, g\in C^1(X),\,\, h\in C^1(Y)\)

\phi(x,y)=c(x,y)+g(x)+h(y)

If \(F(x)\coloneqq\inf_{y\in Y}\phi(x,y)\) is convex on every \(c\)-segment \(t\mapsto (x(t),y)\) satisfying \(x(0)=\argmin_{x\in X} \phi(x,y)\), then \(\phi\) satisfies the FPP.

"... \(F(x)-\lambda\phi(x,y)\) ..." \(\leadsto\) \(\lambda\)-FFP.

Intrinsic: \(c\)-segments and \(F\).

1. Alternating minimization

2. The Kim–McCann geometry

3. Applications

Riemannian/metric space setting

da Cruz Neto, de Lima, Oliveira ’98

Bento, Ferreira, Melo ’17

2. Explicit: \(\phi(x,y)=\frac{1}{2\tau} d_M^2(x,y)+h(y),\quad f(x)=\inf_y\phi(x,y)\)

\[x_{n+1}=\exp_{x_n}\big(-\tau\nabla f(x_n)\big)\]

\(\operatorname{Riem}\geq 0\): \(\nabla^2f\geq 0\) gives \(O(1/n)\) convergence rates

\(\operatorname{Riem}\leq 0\): if \(d_M^2(x,y)\) has nonpositive cross-curvature then convexity of \(f\) on \(c\)-segments gives \(O(1/n)\) convergence rates

Riemannian manifold \(X=Y=M\)

1. Implicit: \(\phi(x,y)=\frac{1}{2\tau} d_M^2(x,y)+f(x)\)

\[x_{n+1}=\argmin_{x} f(x)+\frac{1}{2\tau}d_M^2(x,x_n)\]

\(\operatorname{Riem}\leq 0\): \(\nabla^2f\geq 0\) gives \(O(1/n)\) convergence rates

\(\operatorname{Riem}\geq 0\): if \(d_M^2(x,y)\) has nonnegative cross-curvature then convexity of \(f\) on \(c\)-segments gives \(O(1/n)\) convergence rates

Wasserstein gradient flows, generalized geodesics (Ambrosio–Gigli–Savaré '05)

Global rates for Newton's method

Newton's method: new global convergence rate.

New condition on \(F\) similar but different from self-concordance

T H E O R E M (FL–PCAF '23)

If \(F\) is convex on the paths \(x(t)=(\nabla u)^{-1}(y(t))\) with \(y(t)\) standard segments, then

\[F(x_n)\leq F(x)+\frac{u(x_0|x)}{n}\]

\(\longrightarrow\) Natural gradient descent:

\[x_{n+1}-x_n=-\nabla^2u(x_n)^{-1}\nabla F(x_n)\]

\begin{aligned} \phi(x,y)&=u(y|x)+h(y)\\ F(x)&=\inf_y\phi(x,y) \end{aligned}

Thank you!

Reference:

Gradient descent with a general cost. Flavien Léger and Pierre-Cyril Aubin-Frankowski. arXiv:2305.04917, 2023