Taylor expansions for entropic transport
Flavien Léger
joint work with:
Pierre Roussillon, François-Xavier Vialard and Gabriel Peyré

Background on optimal transport
$$\mathrm{OT}_0(\mu,\nu)=\inf_{\pi\in\Pi(\mu,\nu)}\iint c(x,y)d\pi(x,y)$$
Primal formulation
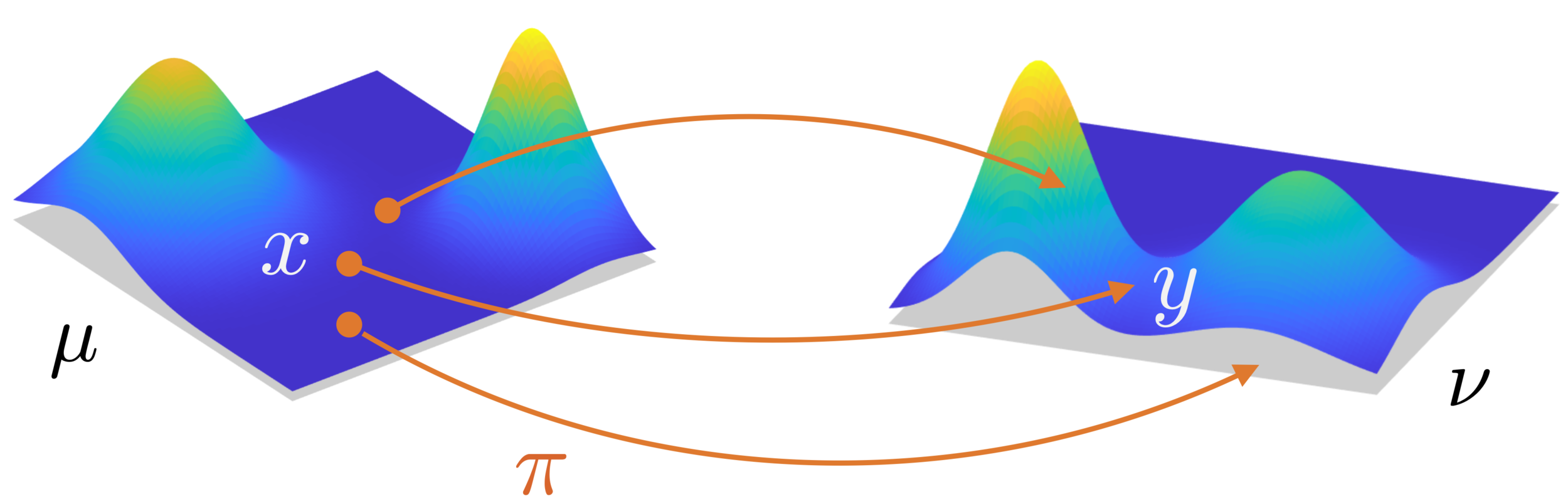
Optimal transport
\(\Pi(\mu,\nu)\): probability measures with marginals \(\mu\) and \(\nu\).
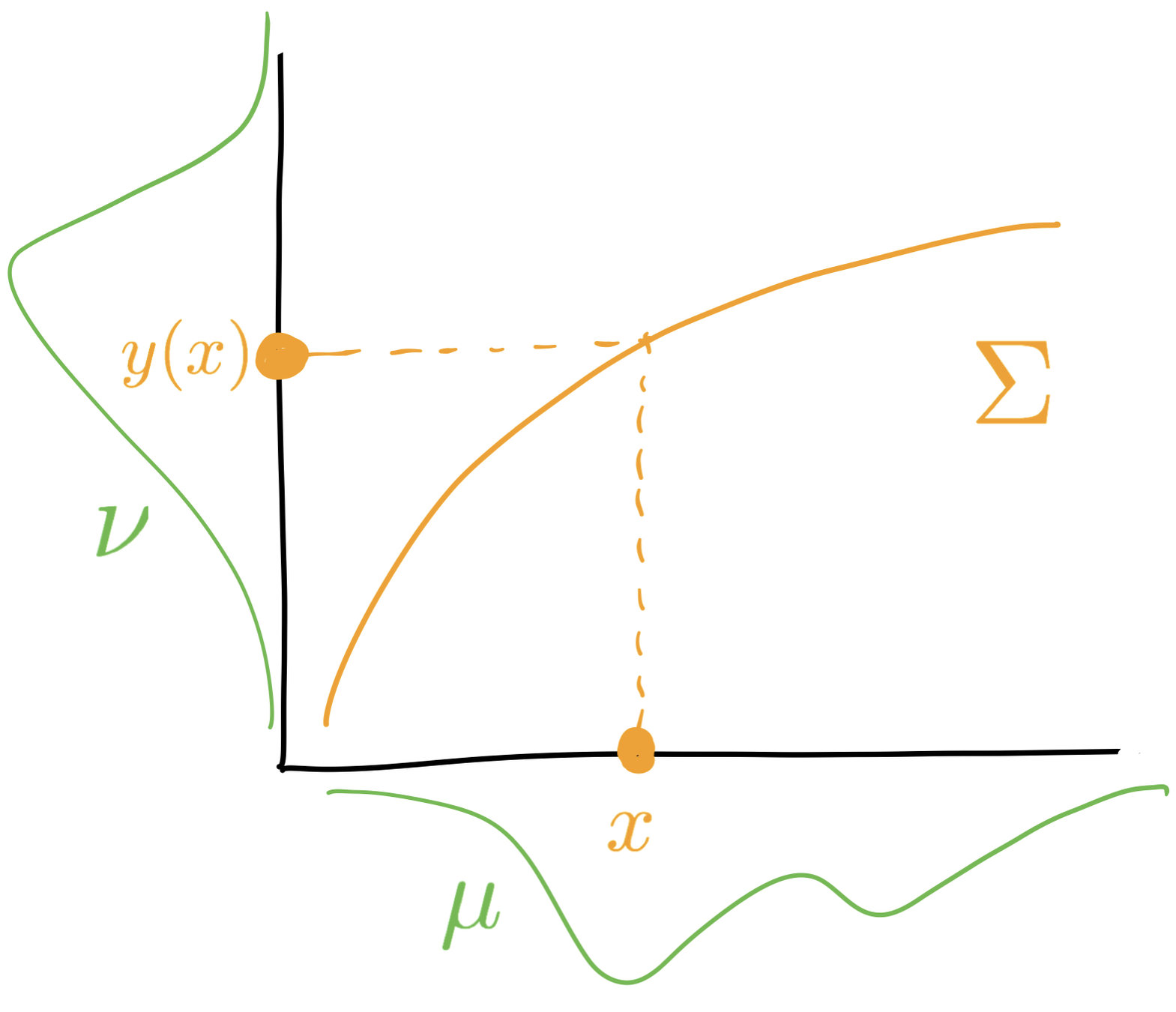
We assume that
$$\Sigma:=\mathrm{supp}\,\pi=\{(x,y(x)),x\in X\}$$
Optimal transport
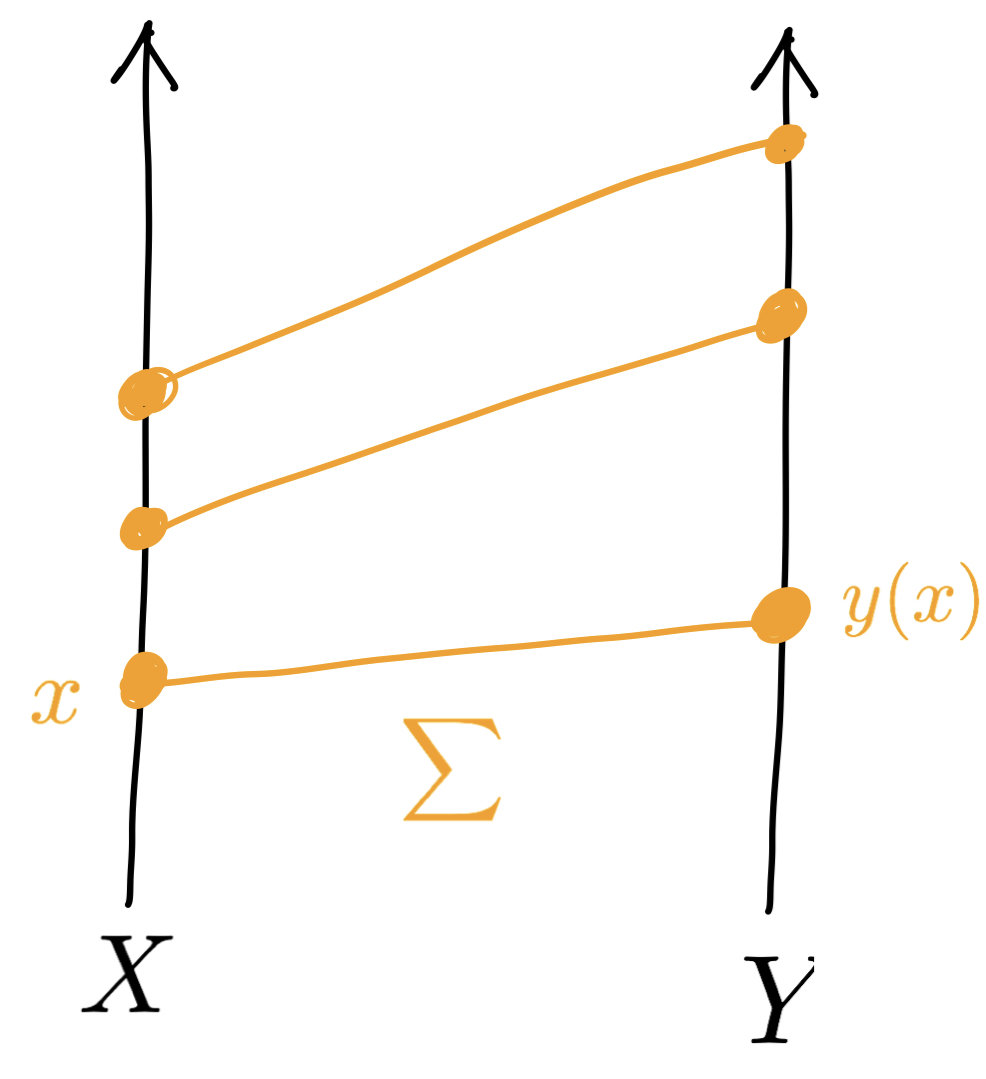
$$X$$
$$Y$$
Optimal transport
Dual formulation
$$\mathrm{OT}_0(\mu,\nu) = \sup_{\phi,\psi}\int\phi\,d\nu - \int\psi\,d\mu$$
s.t.
$$u(x,y):=c(x,y)+\psi(x)-\phi(y)\ge 0$$
The \(c\)-divergence
$$u(x,y)=c(x,y)+\psi(x)-\phi(y)\ge 0$$
$$\Sigma = \{(x,y) : u(x,y) = 0\}$$
Example: \(c(x,y)=-x\cdot y\)
$$u(x,y)=\psi(x)-\phi(y)-x\cdot y$$
$$=\psi(x|x(y))$$
Bregman divergence
$$\mathrm{OT}_\varepsilon(\mu,\nu)=\inf_{\pi\in\Pi(\mu,\nu)}\iint c(x,y)d\pi(x,y) + \varepsilon H(\pi|\mu\otimes\nu)$$
Entropic transport
Primal formulation
\(\pi_\varepsilon\) vs \(\pi_0\)?
Q U E S T I O N

$$X$$
$$Y$$
$$\mathrm{OT}_\varepsilon(\mu,\nu)=\sup_{\phi,\psi}\int\phi\,d\nu-\int\psi\,d\mu-\varepsilon\ln\Big(\iint e^{-\frac1\varepsilon (c+\psi-\phi)}d\mu d\nu\Big)$$
Dual formulation
Entropic transport
$$\longrightarrow \pi_\varepsilon(x,y) = e^{-\frac1\varepsilon(c(x,y)+\psi_\varepsilon(x)-\phi_\varepsilon(y))}\mu(x)\nu(y)$$
Solve with Sinkhorn: \(\phi^n \to \psi^n\to\phi^{n+1}\to\dots\)
Our question
\(\pi_0\) singular measure supported on \(\Sigma\)
\(\pi_\varepsilon\) smooth measure supported on \(X\times Y\)
$$\mathrm{OT}_0(\mu,\nu)$$
$$\mathrm{OT}_\varepsilon(\mu,\nu)$$


What's known
- In general $$\phi_\varepsilon\to\phi_0\quad\text{as }\varepsilon\to 0$$ (Nutz & Wiesel ’21, Berman ’21, N Gigli & L Tamanini ’18)
- For general costs $$\mathrm{OT}_\varepsilon(\mu,\nu)\approx\mathrm{OT}_0(\mu,\nu)-\varepsilon\ln(2\pi\varepsilon)^{d/2}-\varepsilon H(\nu|m)$$ (S Pal ’19)
- For quadratic costs (Schrödinger problems )$$\mathrm{OT}_\varepsilon(\mu,\nu)\approx\mathrm{OT}_0(\mu,\nu)-\varepsilon\ln(2\pi\varepsilon)^{d/2}-\frac\varepsilon 2(H(\mu)+H(\nu))$$ $$+\frac{\varepsilon^2}{8} \int_0^1 \mathrm{FI}(\rho_t)\,dt$$ (G Conforti & L Tamanini ’21)
Background on the Kim–McCann geometry
(YH Kim & RJ McCann ’10)
Riemannian metric \(g\) on \(\Sigma\)
$$c(x,y)+c(x+\xi,y+\eta) \le c(x+\xi,y)+c(x,y+\eta)$$
\(\lvert\xi\vert,\lvert\eta\rvert\ll 1\) yields
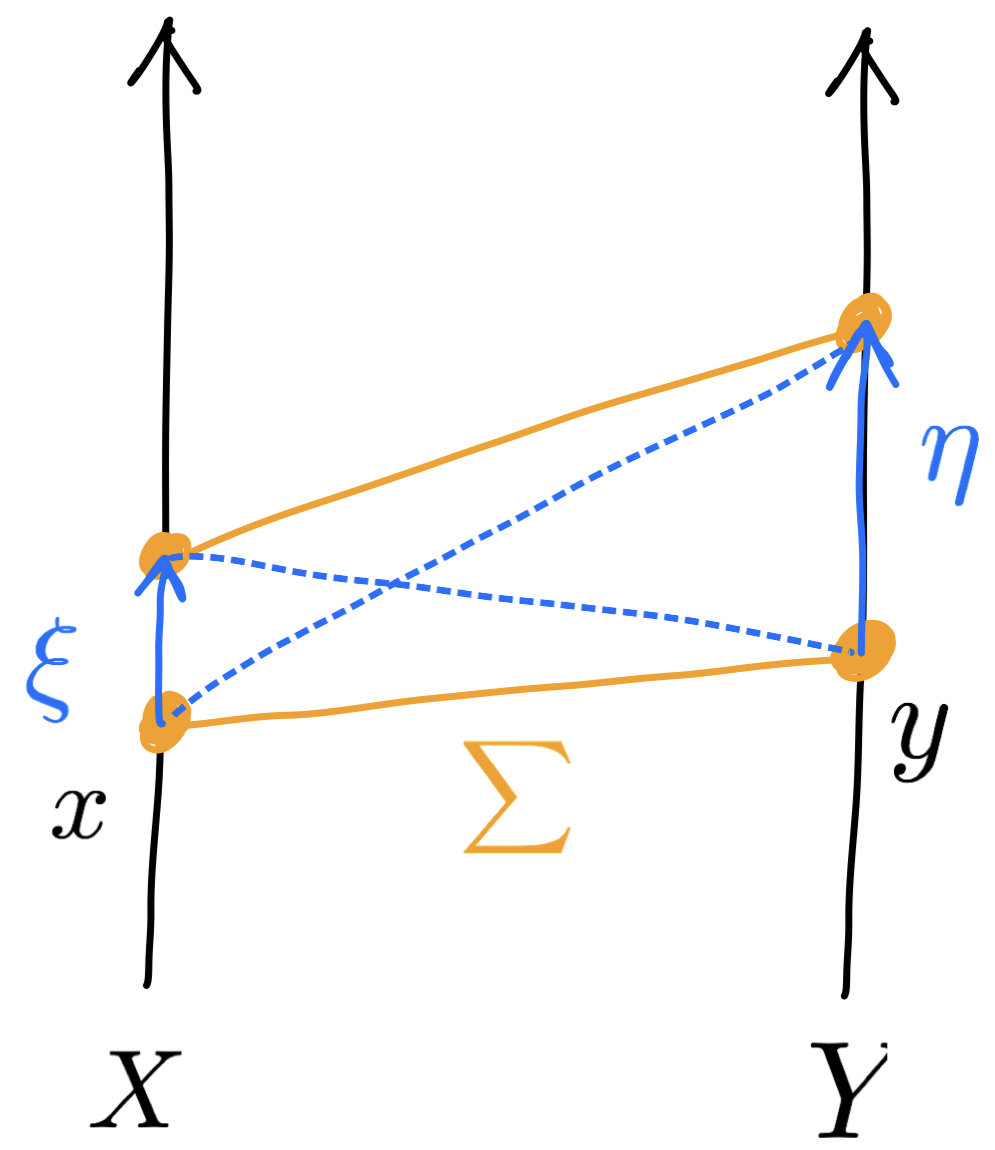
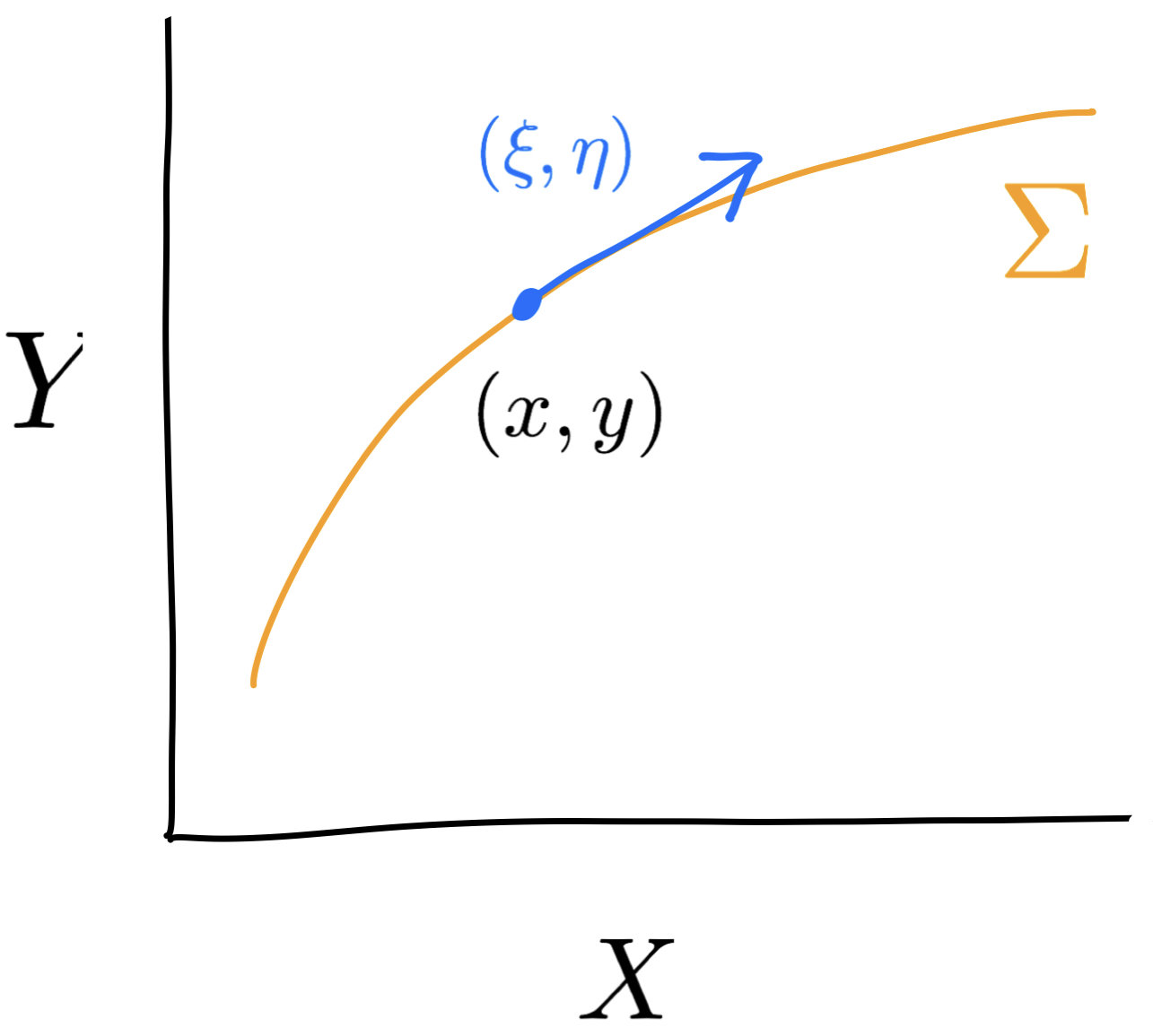
$$-D_{xy}^2c(x,y)(\xi,\eta)\ge 0$$
Quantifying a matching's stability
Kim and McCann's idea:
consider $$\hat g = -D^2_{xy}c$$ as a semi-metric over all \(X\times Y\)
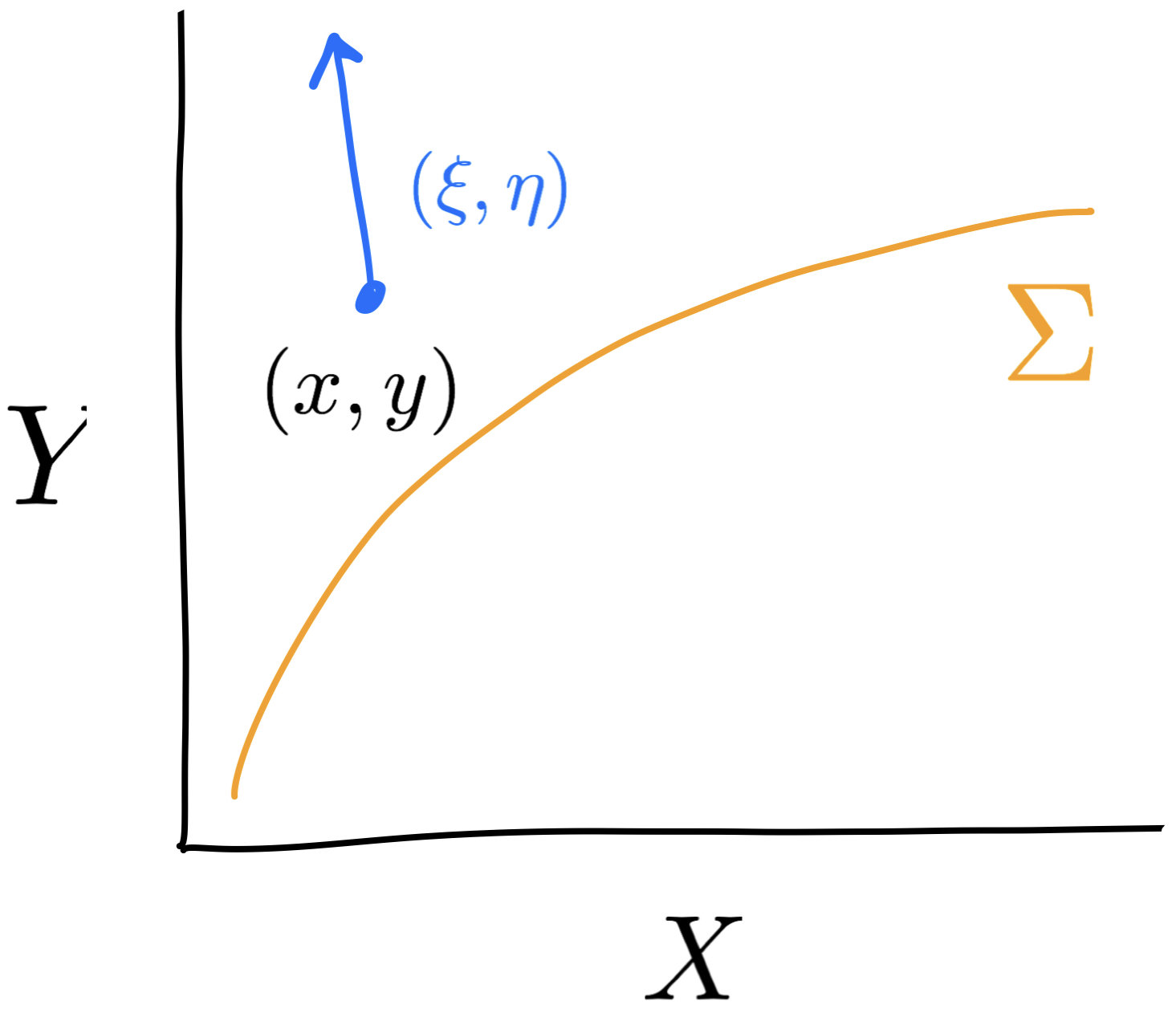
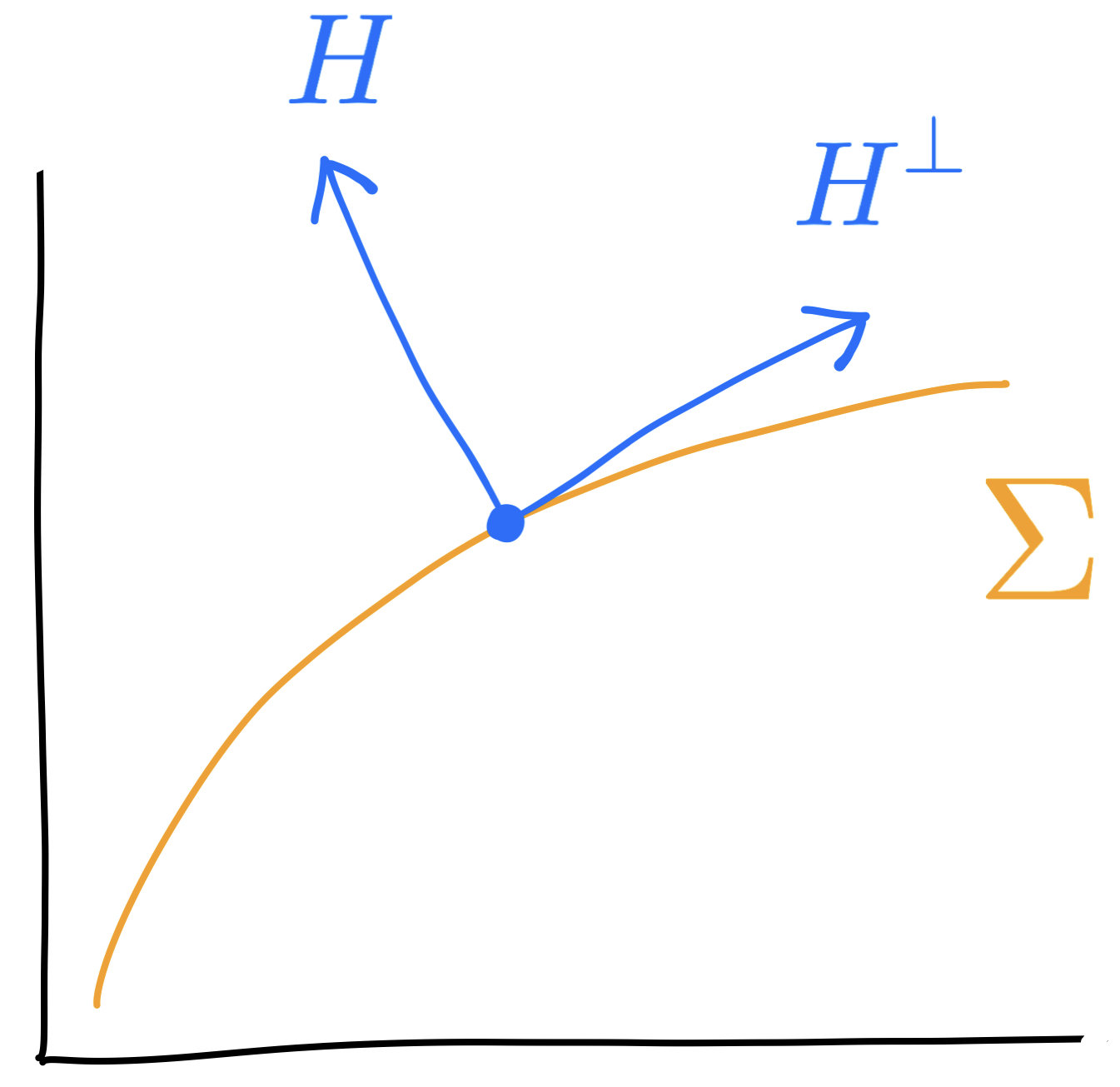
Second fundamental form
$$h(U,V)=(\hat\nabla_UV)^\perp$$
Mean curvature \(H=\mathrm{tr}(h)\) (a normal vector field)
$$(T\Sigma\times T\Sigma\to T^\perp\Sigma)$$
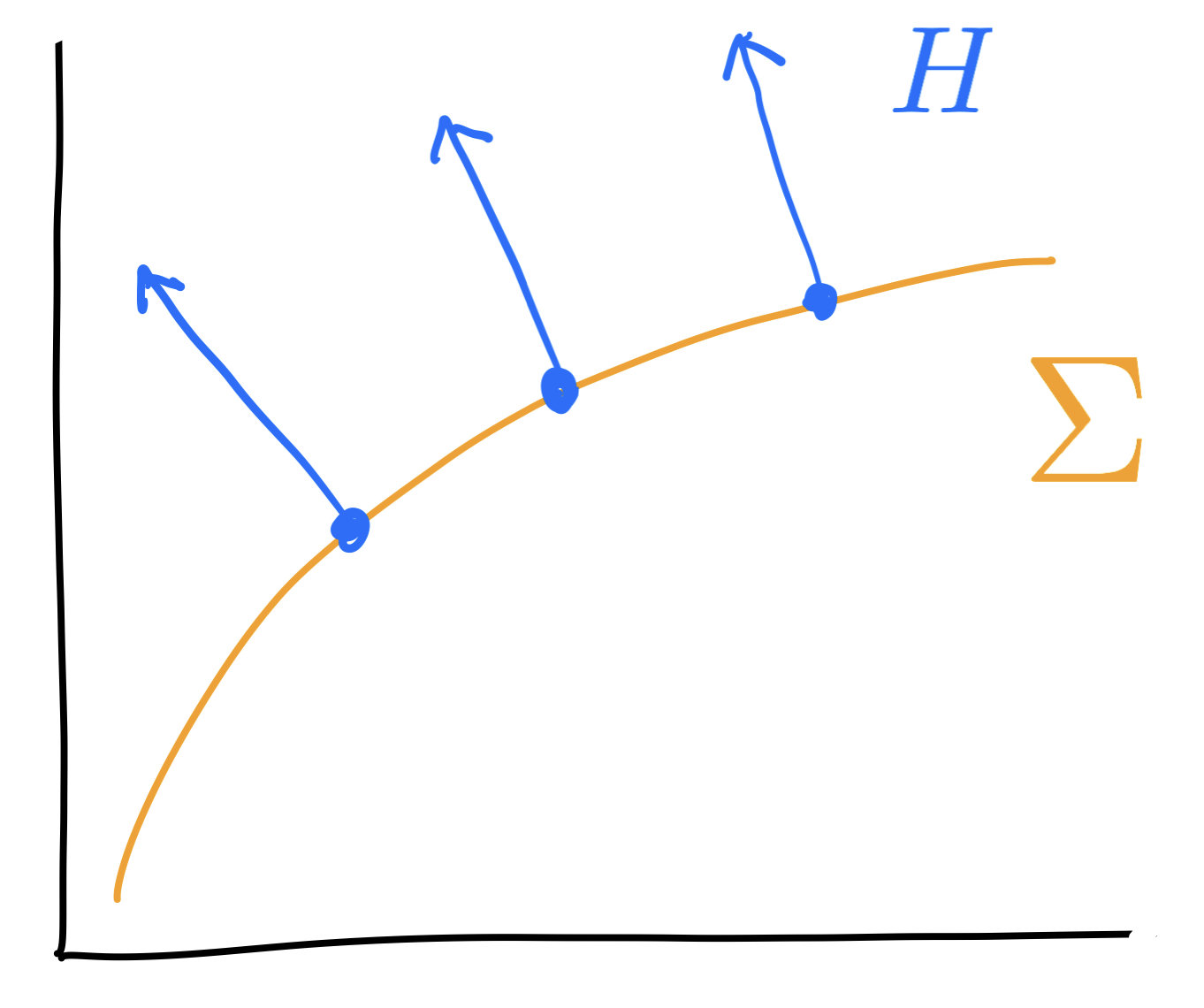
Additional structure: para-Kähler manifold
\((\cdot)^\perp\) maps \(T^\perp\Sigma\) to \(T\Sigma\)
Example: \(c(x,y)=-x\cdot y\)
$$\hat g=\begin{pmatrix}0&I_d\\I_d&0\end{pmatrix}$$
$$u(x,y)=\psi(x)-\phi(y)-x\cdot y$$
$$=\psi(x|x(y))$$
Bregman divergence
$$g=D^2\psi$$
Hessian metric
flat metric
In summary, we have
On \(X\times Y\)
On \(\Sigma\)
Extrinsic curvatures
\(\hat g\) semi-metric
\(\hat m\) volume form
\(\hat \nabla\) Levi-Civita connection
\(\hat R\) scalar curvature
\(g\) metric
\(m\) volume form
\(\nabla\) Levi-Civita connection
\(R\) scalar curvature
\(h\) second fundamental form
\(H\) mean curvature
A new Laplace formula
$$\iint_{X\times Y}\frac{e^{-u(x,y)/\varepsilon}}{(2\pi\varepsilon)^{d/2}}f(x,y)\,d\hat m(x,y) = \int_\Sigma fdm\,+$$
$$\varepsilon\int_\Sigma \bigg[-\frac 18\hat\Delta f+ \frac 14 \hat\nabla_{\!H} f+ \frac{1}{16}\Big( |H|^2 - \frac{5}{3}|h|^2 -R + \frac{3}{4}\hat R\Big)f\bigg] \,dm + \varepsilon^2\mathcal{R}(\varepsilon)$$
T H E O R E M
\(u\) vanishes on \(\Sigma\)
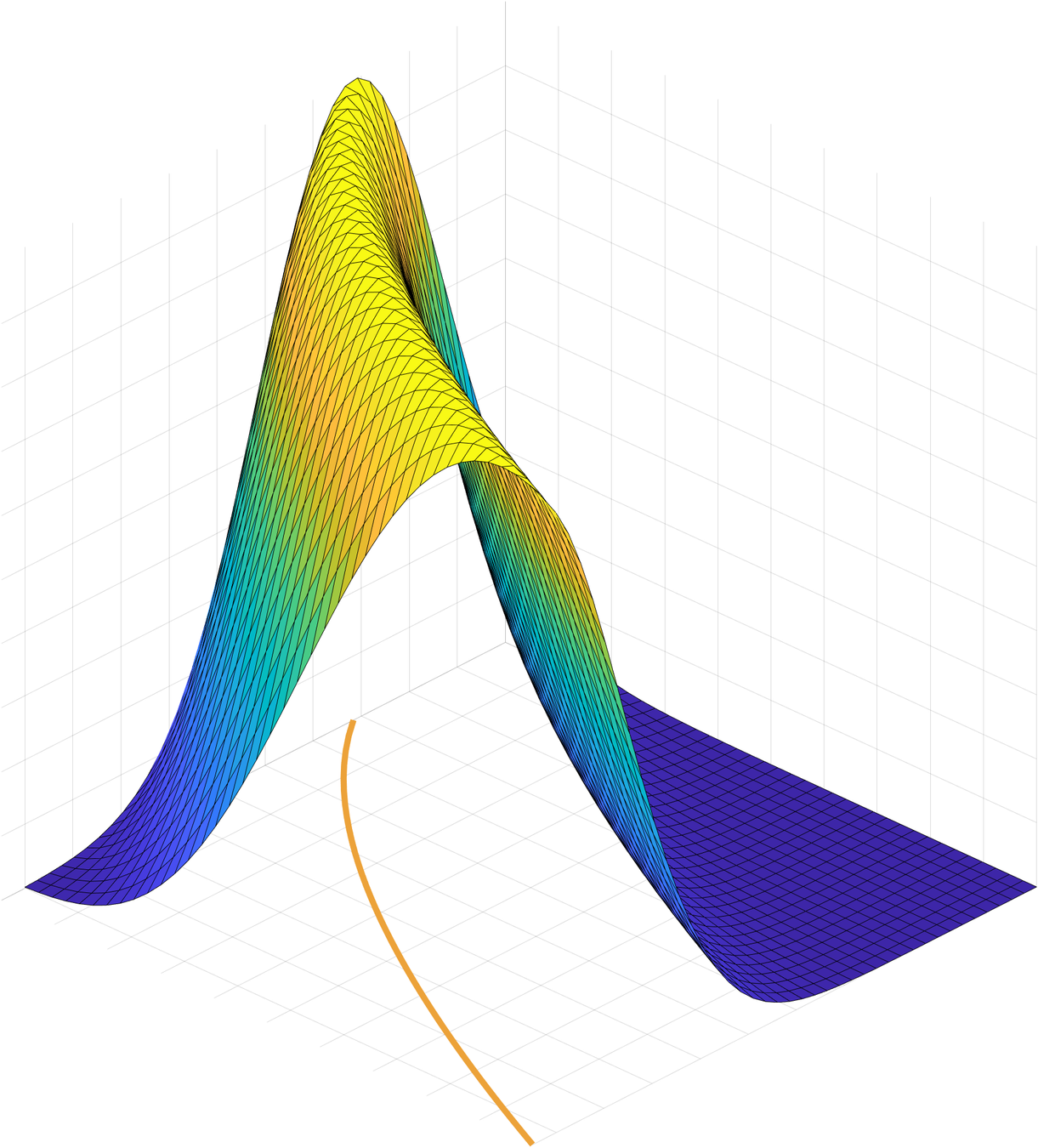
$$\Sigma$$
$$e^{-u(x,y)/\varepsilon}$$
$$X$$
$$Y$$
Assumptions:
$$X=Y=\mathbb{R}^d$$
$$0<\lambda\le D^2u\le\Lambda$$
$$f\textrm{ and } D^2u \in W^{4,\infty}$$
Novelties:
1. Geometric expression
2. Quantitative remainder bound
$$\lvert\mathcal{R}(\varepsilon) \rvert \le C \lVert D^2u\rVert_{W^{4,\infty}}^4 \iint_{X\times Y} \frac{e^{-\lambda\lvert y-y(x)\rvert^2/2\varepsilon}}{(2\pi\varepsilon/\lambda)^{d/2}} \lvert D_{\le 4}f\rvert (x,y)\,d\hat{m}(x,y)$$
Taylor expansion of the potentials
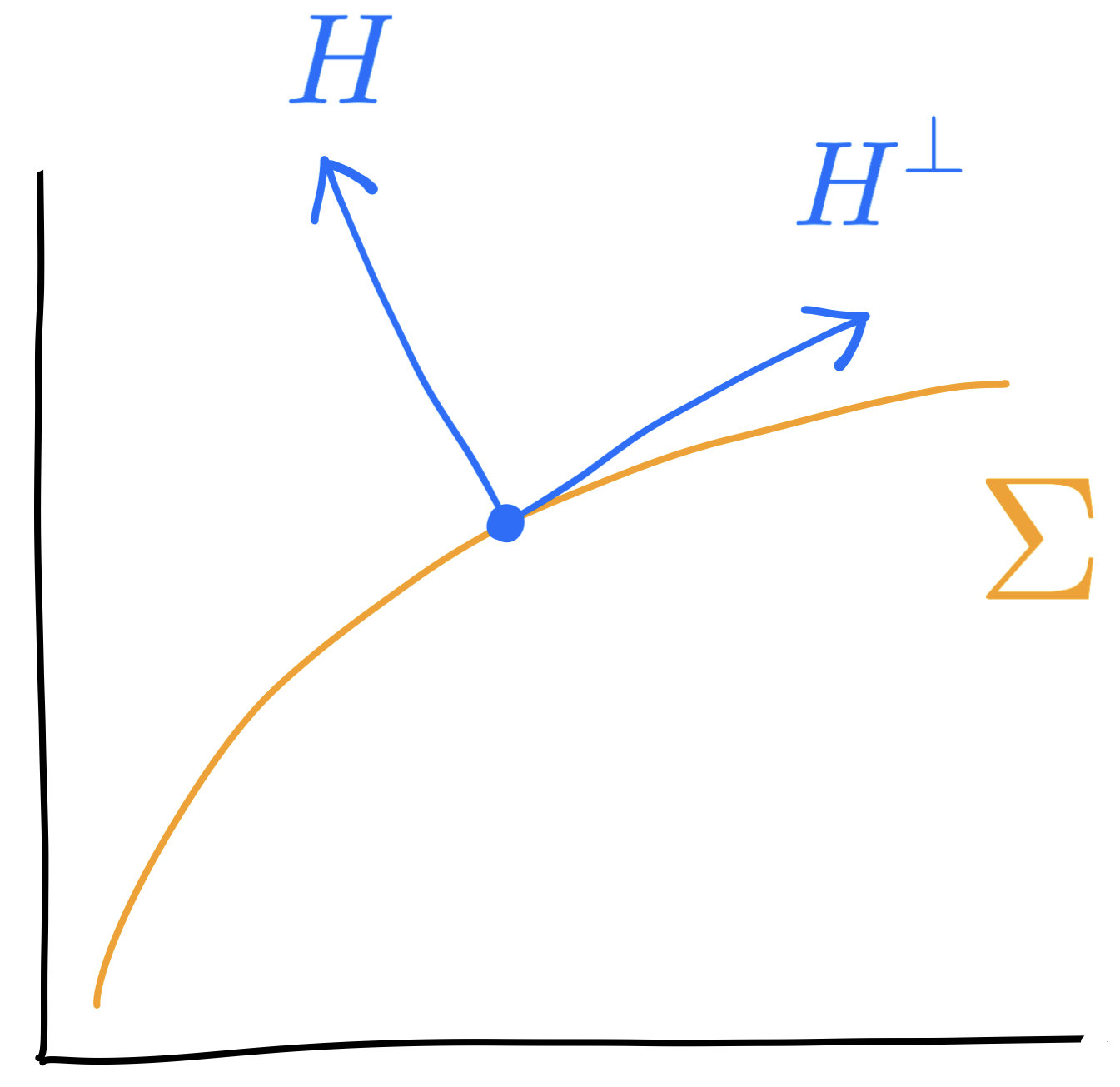
$$\mathrm{div}_\pi(\nabla V)=\mathrm{div}_\pi(H^\perp)$$
\(H\) : mean curvature, \(H^\perp\) tangent to \(\Sigma\)
Solve for \(V\) on \(\Sigma\)
\(\pi\) : optimal transport plan
(supported on \(\Sigma\))
$$\int_\Sigma \mathrm{div}_\pi(\xi) f\,d\pi = -\int_\Sigma\xi\cdot\nabla f\,d\pi$$
D E F I N I T I O N
$$\mathrm{div}_\pi(\nabla V)=\mathrm{div}_\pi(H^\perp)$$
$$\psi_\varepsilon=\psi_0+\frac\varepsilon 2\ln\Big(\frac{m}{e^{-V}\mu}\Big) + o(\varepsilon)$$
T H E O R E M
$$u(x,y)\approx -\varepsilon \ln\bigg(\frac{\sqrt{e^{-V(x)}e^{-V(y)}}\,\pi_\varepsilon(x,y)}{\sqrt{m(x)\mu(x) m(y)\nu(y)}}\bigg)$$
Assumptions:
$$X=Y=\mathbb{R}^d$$
$$0<\lambda\le D^2u\le\Lambda$$
Log-concavity control over \(\mu\) and \(\nu\)
\((\psi_\varepsilon)_\varepsilon\) uniformly bounded in \(H^5\)
Taylor expansion of the transport value
$$\mathrm{OT}_\varepsilon(\mu,\nu)=\mathrm{OT}_0(\mu,\nu) - \varepsilon\ln(2\pi\varepsilon)^{d/2}-\varepsilon H(\pi|m)$$
$$+\frac{\varepsilon^2}{8} \int_\Sigma \Big[\lvert\nabla\ln(\pi/m)\rvert^2+\frac 14 \hat{R}+R+\frac{5}{3}|h|^2 -|\nabla V|^2\Big]d\pi + o(\varepsilon^2)$$
T H E O R E M
Example: Quadratic cost \(c(x,y)=|x-y|^2\)
\(\varepsilon^2\) term was known (Conforti–Tamanini):
$$\frac{\varepsilon^2}{8} \int_0^1 \mathrm{FI}(\rho_t)\,dt$$
$$\frac{\varepsilon^2}{8} \int_\Sigma \Big[\lvert\nabla\ln(\pi/m)\rvert^2+R+\frac{5}{3}|h|^2 -|H|^2\Big]d\pi$$
We found:
Strategy of proof
\(\psi_\varepsilon\) : solution to dual problem $$\displaystyle\max_\psi J_\varepsilon(\psi)$$ \(\widetilde\psi_\varepsilon\) : competitor
Proof strategy
Step one
$$c\lVert \nabla h\rVert^2_{L^2}-\varepsilon\,c \lVert \nabla h\rVert_{H^3}^2 \le -\delta^2\!J_\varepsilon(\psi)(h,h)$$
Step two
Choose competitor \(\widetilde\psi_\varepsilon\) such that
$$\delta J_\varepsilon(\widetilde\psi_{\varepsilon})h \le C \varepsilon^2 \lVert \nabla h\rVert_{H^3}$$
Implies
$$c\lVert \nabla \psi_\varepsilon - \nabla\widetilde\psi_\varepsilon \rVert^2_{L^2}-\varepsilon\,c \lVert \nabla \psi_\varepsilon - \nabla\widetilde\psi_\varepsilon\rVert_{H^3}^2 \le -\langle\delta J_\varepsilon(\psi_\varepsilon) - \delta J_\varepsilon(\widetilde\psi_\varepsilon), \psi_\varepsilon - \widetilde\psi_\varepsilon \rangle$$
Thanks!
The research leading to these results has received funding from the European Research Council under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement no. 866274)