magnetismo
esempi di forze magnetiche
Magneti permanenti
elettromagneti
introduzione al campo magnetico

"Analogamente al caso del campo elettrico \( \vec{E} \), è possibile introdurre un campo magnetico \( \vec{B} \). Tuttavia la definizione di \( \vec{B} \) risulta essere differente rispetto a quella di \( \vec{E} \)"
campo magnetico terrestre

CAMPO ELETTRICO E CAMPO MAGNETICO


\[\vec{F}_{el} = q \vec{E} \]
\[ \vec{F}_{mag} = q \, (\vec{v} \times \vec{B}) \]

DEFINIZIONE DI PRODOTTO VETTORIALE

MOTO IN UN CAMPO MAGNETICO COSTANTE
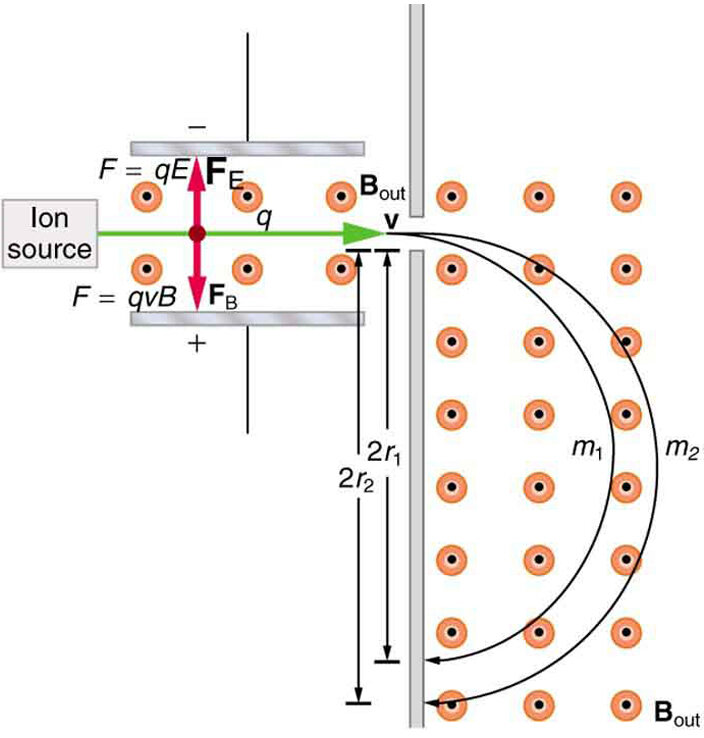
campo magnetico: il ciclotrone
CAMPO MAGNETICO: FORZA MAGNETICA SU UN FILO ATTRAVERSATO DA CORRENTE
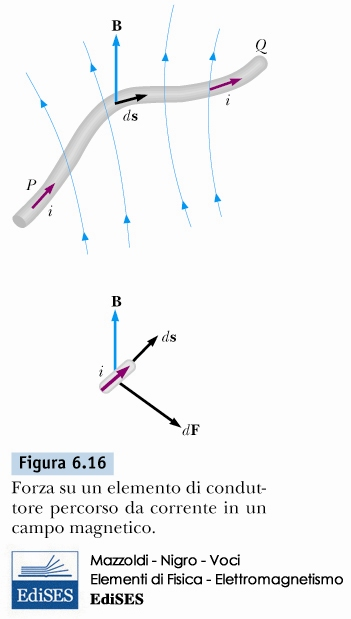
\[ d \vec{F}_{mag} = i \, d \vec{s} \times \vec{B} \]
SORGENTI DEL CAMPO MAGNETICO
LEGGE DI BIOT-SAVART
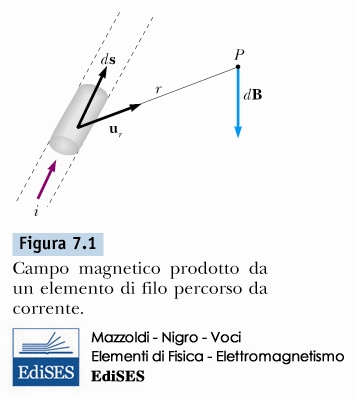
\[ d \vec{B} = \frac{\mu_{0}}{4 \pi} \frac{i \, d \vec{s} \times \vec{u}_{r} }{r^{2}} \]
CAMPO DI UN FILO INFINITO PERCORSO DA CORRENTE
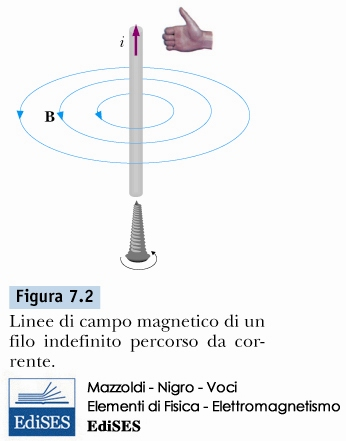
\[ B = \frac{\mu_0 \, i}{2 \pi R} \]
legge di ampere
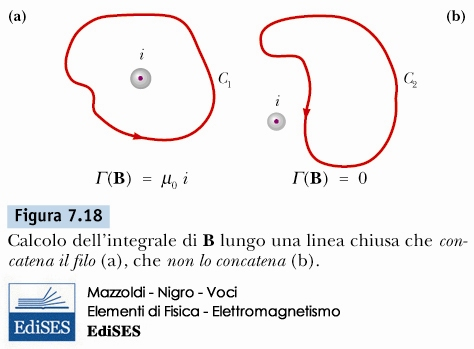
\[ \oint_S \vec{B} \cdot d \vec{s} = \mu_{0} i \]
i solenoidi: 1


i solenoidi: 2

solenoidi, campo magnetico e teorema di ampere
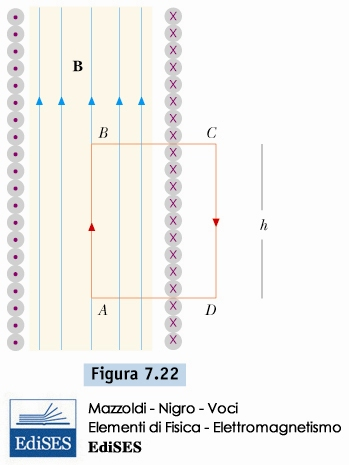
\[ B = \mu_{0} \, i \, n \]
\[ n = avvolgimenti \, per \, unità \, di \, lunghezza \]
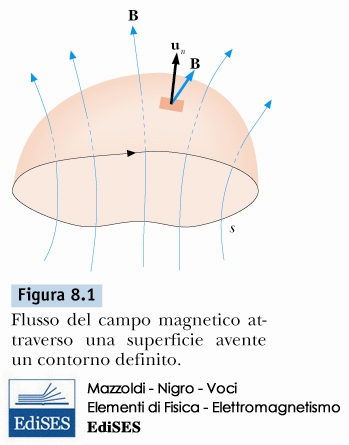
flusso del campo magnetico
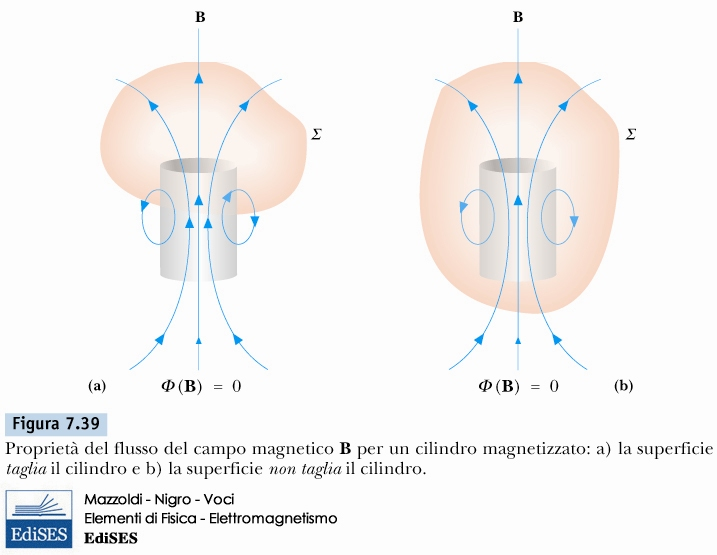
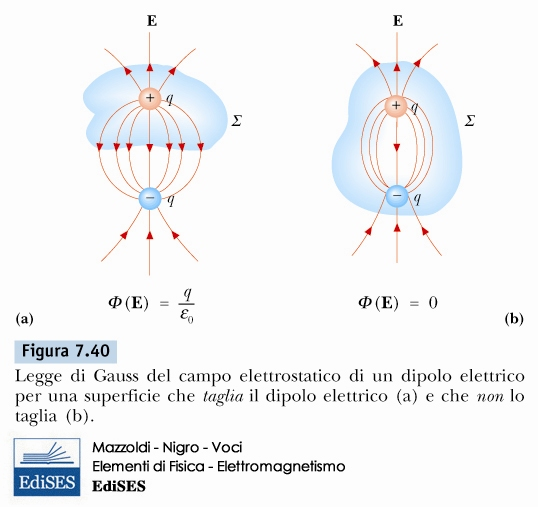
\[ \Phi_{B} = \int_{A} \vec{B} \cdot d\vec{A} = 0 \]
legge di faraday: induzione elettromagnetica
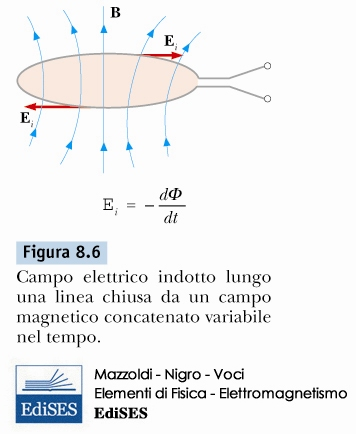
\[ -\frac{d \Phi_{B}}{dt} = \oint_S \vec{E} \cdot d \vec{s} = \mathcal{E} \]