termodinamica: 1
termologia e termometria
termodinamica: nuovi concetti
- Temperatura \( (T) \, \Rightarrow \) Caldo vs Freddo \( \Rightarrow [^{\circ}C,K] \)
- Calore \( (Q) \, \Rightarrow \) Una nuova forma di energia \( \Rightarrow [J] \)
- Pressione \( (P) \, \Rightarrow \, \frac{F}{S} \, \Rightarrow \, [N/m^{2} = Pa, Atm \approx 10^5 Pa] \)
- Entropia \( (S) \, \Rightarrow \) Ordine ed energia utile \( \Rightarrow [J/K] \)
termodinamica: perché?
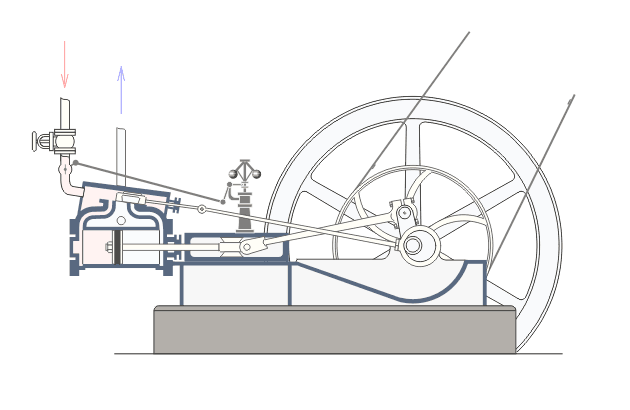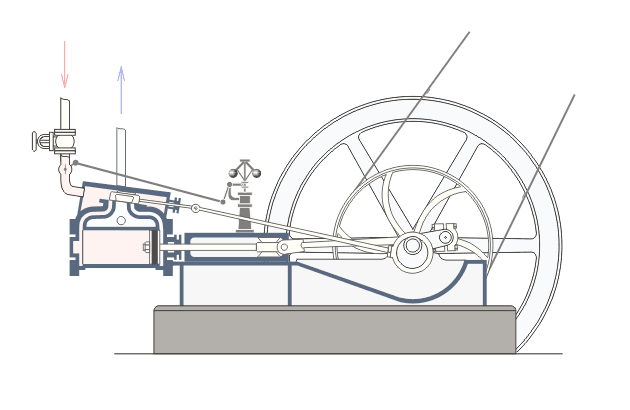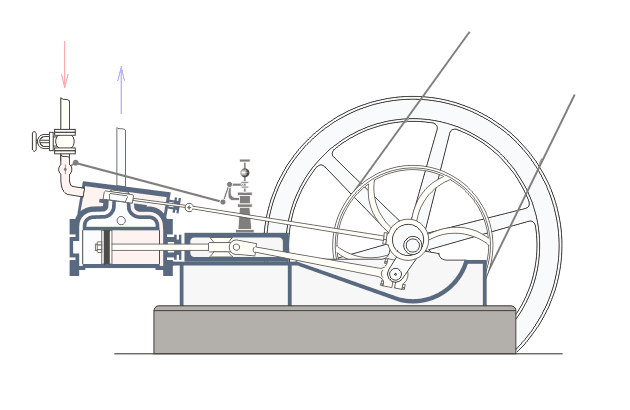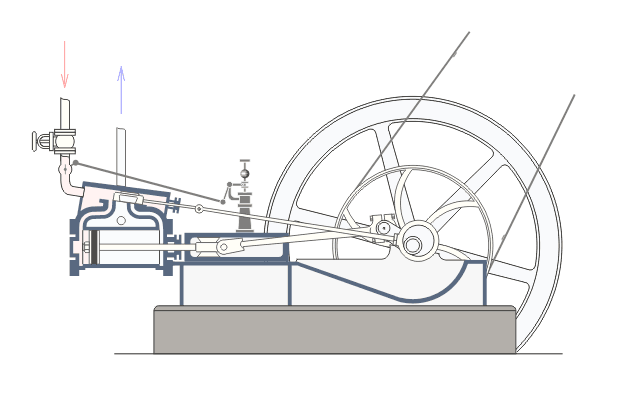
STORICAMENTE
- Macchine a vapore
PER NOI
- Dilatazione termica
- Cambiamenti di fase
- Entropia e stabilità dei sistemi
pressione
- \( P = \frac{F}{S} \, [N/m^2 = Pa] \)
- \( P(\vec{r}) = \frac{dF}{dS} \, [N/m^2 = Pa] \)
- \( 1 atm = 101325 Pa \)
- La pressione in un fluido all'equilibro è scalare ed isotropa
temperatura
PROPRIETÀ TERMOMETRICHE
- Dilatazione termica dei metalli
- Resistenza elettrica
- Colore dell'emissione luminosa
- Pressione di un gas a volume costante
CALIBRAZIONE A DUE PUNTI FISSI
- Acqua e ghiaccio fondente \( \Rightarrow 0^{\circ}C \)
- Acqua vapore acqueo \( \Rightarrow 100^{\circ}C \)




principio zero della termodinamica
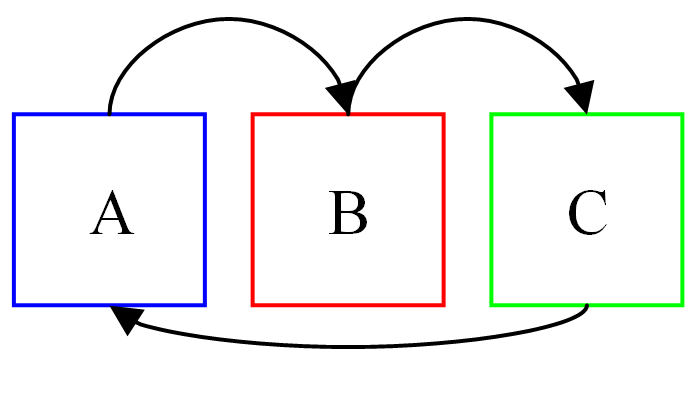
Se due corpi A e B sono in contatto termico tra loro (possono scambiarsi calore), allora all'equilibro assumeranno la stessa temperatura
Se un corpo A è in equilibrio termico con un corpo C e anche un altro corpo B è in equilibrio termico con C, allora A e B sono in equilibrio termico tra loro.
termometria, gas e temperatura assoluta

\( P(T_{C}) = P_{0}(1 + \alpha T_{C}), \, \alpha = \frac{1}{273,15} [\frac{1}{ ^{\circ} C}] \)
\( \Downarrow \)
\( T_{K} = T_{C} - 273,15 \)
\( \Downarrow \)
\( P(T_{K}) = P_{0} \alpha T_{K} \)
\( \Downarrow \)
\( T_{K} = 0 \, K \Rightarrow \) zero assoluto in \( Kelvin \)
\( 1^{\circ} C = 1 \, K \)
calore specifico

Stessa sostanza
\[ T_{eq} = \frac{\sum_{i}m_{i}T_{i}}{\sum_{i}m_{i}} \]
Diversa sostanza
\[ T_{eq} = \frac{\sum_{i}c_{i}m_{i}T_{i}}{\sum_{i}c_{i}m_{i}}, \, c_{H_{2}O} = 1 \]
\( c \Rightarrow \) calore specifico
\( C = c \cdot m \Rightarrow \) capacità termica
calore scambiato
\[ Q_{i} = m_{i}c_{i}(T_{eq} - T_{i}) \]
\[ \sum_{i}Q_{i} = 0 \]
\[ 1 \, Kcal = 4186 J \]
calore specifico: caso generale
\[ dQ = m \cdot c(T) \cdot dT \]
\[ c(T) = \frac{1}{m} \frac{dQ}{dT} \]
\[ c_{trasf} = \frac{1}{m} \left( \frac{dQ}{dT} \right)_{trasf} \]
calori latenti e cambiamenti di fase

Calore latente di fusione
\[ Q_{f} = m \lambda_{f} \]
Calore latente di evaporazione
\[ Q_{e} = m \lambda_{e} \]