Machine Learning Basics

Deep Learning Book - Ch 5

Disclaimer

There is math.

There is theory.

There is pseudocode.

A lot of content in 60min

Interact with us!

"M.L. is easy!11!"

"M.L. is easy!11!"

\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_0^i)
1m∑i=1m((h(xi)−yi)x0i)\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_0^i)
\theta_0
θ0\theta_0
-\alpha
−α-\alpha
\theta_0 =
θ0=\theta_0 =
\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_1^i)
1m∑i=1m((h(xi)−yi)x1i)\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_1^i)
\theta_1
θ1\theta_1
-\alpha
−α-\alpha
\theta_1 =
θ1=\theta_1 =
\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_2^i)
1m∑i=1m((h(xi)−yi)x2i)\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_2^i)
\theta_2
θ2\theta_2
-\alpha
−α-\alpha
\theta_2 =
θ2=\theta_2 =
\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_n^i)
1m∑i=1m((h(xi)−yi)xni)\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_n^i)
\theta_n
θn\theta_n
-\alpha
−α-\alpha
\theta_n =
θn=\theta_n =

I'm Hanneli

I'm Gustavo

Goals

  • Go over the main topics of Ch. 5
  • Connect the missing pieces
  • Show the relation between ML theory, Statistics and implementation

Agenda

  • Definition of "Learning Algorithm" (Gustavo)
  • Application examples (Gustavo)
  • Linear Regression demystified (Hanneli)
  • Factors for the success of a learning algorithm (Hanneli)
  • Useful concepts from Statistics (Gustavo)
  • Code time - examples with Octave/Python (Hanneli)
  • Extras and References

General idea

Training set

Learning Algorithm

hypothesis

input

predicted output

General Idea

Training set

Learning Algorithm

hypothesis

input

predicted output

What do we

mean by that?

Learning Algorithm

"A program learns from an experience E with respect to some class of tasks T and performance measure P, if P at T improves with E"

T - Task

How a ML system should perform an example

Example - Collection of features (quantitative measured)

  • Classification (tag people)
  • Transcription (speech recognition)
  • Machine Translation (translate)
  • Structured output (natural lang)
  • Anomaly detection (flag atypical)
  • Synthesis (video game textures)
  • Denoising (predict clean example)

P - Performance Measure

Quantitative performance measure of the algorithm

Factors

a) Accuracy

b) Error Rate

P is specific to a task T

E - Experience

Kind of experience during the learning process

Supervised Learning

Unsupervised Learning

Reinforcement Learning

We have an idea of the right answer for what we are asking. Example: Given a picture of a person, predict how old is he/she

We have no idea of the right answer for what we are asking. Example: Given a collection of items you don't know, try to group them by similarity.

Let the machine take control of the context and you provide input feedback.

Example: Reduce items in stock by creating dynamic promotions

Problem:

Sell used cars. Find the best price to sell them (not considering people who collect old cars)

Do we have any idea for know relations?

older -> cheaper

unpopular brands -> cheaper

too many kms -> cheaper

Problem:

Sell used cars. Find the best price to sell them (not considering people who collect old cars)

What kind of M.L. Algorithm would you use here? (E)

Supervised Learning

Algorithm draft:

Chose one variable to analyse vs what you want to predict (example: year x price). Price is the variable you want to set a prediction. (T)

Come up with a training set to analyse these variables

Number of training examples (m)

input variable or features - x

output variable or target - y

Back to the principle

Training set

Learning Algorithm

hypothesis

input

predicted output

m

x

h

y

Strategy to h

Strategy to h

Linear equation

h = ax + b

How do you choose a and b?

From the training set, we have expected values y for a certain x:

(x^i , y^i )
(xi,yi)(x^i , y^i )

Come up with a hypothesis that gives you

the smallest error for all the training set:

The algorithm

h(x)

y

Your hypothesis 

for an input x

The output of the training set

-

Measure the difference

The algorithm

h(x)

y

Your hypothesis 

for an input x

The output of the training set

-

Measure the difference

for the entire training set (P)

The algorithm

Your hypothesis 

for an input x

The output of the training set

-

Measure the difference

for the entire training set

h(x^i)
h(xi)h(x^i)
y^i
yiy^i

(

)

\sum_{i=1}^{m}
∑i=1m\sum_{i=1}^{m}

The algorithm

Your hypothesis 

for an input x

The output of the training set

-

We don't want to cancel positive and negative values

h(x^i)
h(xi)h(x^i)
y^i
yiy^i
\sum_{i=1}^{m}
∑i=1m\sum_{i=1}^{m}
)^2
)2)^2
(
((
\frac{1}{2m}
12m\frac{1}{2m}

Average

Mean Square Erros (MSE)

The algorithm

-

h(x^i)
h(xi)h(x^i)
y^i
yiy^i
\sum_{i=1}^{m}
∑i=1m\sum_{i=1}^{m}
)^2
)2)^2
(
((
\frac{1}{2m}
12m\frac{1}{2m}

Cost Function

J =

We want to minimize the difference

Understanding it

Understanding it

We can come up with different hypothesis (slopes for h function)

Understanding it

We can come up with different hypothesis (slopes for h function)

Understanding it

That's the difference

h(x^i) -y^i
h(xi)−yih(x^i) -y^i

for a certain cost function

h = ax + b
h=ax+bh = ax + b

Understanding it

That's the difference

h(x^i) -y^i
h(xi)−yih(x^i) -y^i

for another cost function

h = ax + b
h=ax+bh = ax + b

This cost function (J) will be a parabola

Minimum value

on h = ax +b,

we are varying a

J(a)

We also need to vary b. J will be a surface (3 dimensions)

h = ax + b

J(a,b)

Back to the algorithm

Minimize any Cost Function.

plotted in Jan/17

Back to the algorithm

Minimize any Cost Function.

Min

We start with a guess

And 'walk' to the min value

Back to the algorithm

Or:

Min

How do you find the min values of a function?

Calculus is useful here

Calculus - we can get this information from the derivative

\frac{\partial }{\partial a}
∂∂a\frac{\partial }{\partial a}

Remember: we start with a guess and walk to the min value

Back to the cost function

\frac{\partial }{\partial a}J(a,b)
∂∂aJ(a,b)\frac{\partial }{\partial a}J(a,b)
\frac{\partial }{\partial b}J(a,b)
∂∂bJ(a,b)\frac{\partial }{\partial b}J(a,b)

Towards the min value

a_0
a0a_0
b_0
b0b_0

We start with

a guess

-\alpha
−α-\alpha
-\alpha
−α-\alpha

Walk on

the 

graph

a =
a=a =
b =
b=b =

Partial Derivatives

Gradient Descent

\frac{\partial }{\partial a}J(a,b)
∂∂aJ(a,b)\frac{\partial }{\partial a}J(a,b)
\frac{\partial }{\partial b}J(a,b)
∂∂bJ(a,b)\frac{\partial }{\partial b}J(a,b)

Partial derivatives

(min value)

a_0
a0a_0
b_0
b0b_0

We start with

a guess

-\alpha
−α-\alpha
-\alpha
−α-\alpha

Walk on

the 

graph

a =
a=a =
b =
b=b =

Back to the cost function

\frac{\partial }{\partial a}J(a,b)
∂∂aJ(a,b)\frac{\partial }{\partial a}J(a,b)
\frac{\partial }{\partial b}J(a,b)
∂∂bJ(a,b)\frac{\partial }{\partial b}J(a,b)
a_0
a0a_0
b_0
b0b_0
-\alpha
−α-\alpha
-\alpha
−α-\alpha

Learning rate 

(another guess)

a =
a=a =
b =
b=b =

Repeat until convergence

Going back to used cars

We are only analysing year vs price. We have more factors: model, how much the car was used before, etc

Back to the principle

Training set

Learning Algorithm

hypothesis

input

predicted output

m

x

h

Strategy to h

Consider multiple variables: a, b, c,... (or using greek letters) 

h(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3
h(x)=θ0+θ1x1+θ2x2+θ3x3h(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3

Can you suggest the next steps?

Gradient Descent for multiple Variables

\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_0^i)
1m∑i=1m((h(xi)−yi)x0i)\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_0^i)
\theta_0
θ0\theta_0
-\alpha
−α-\alpha
\theta_0 =
θ0=\theta_0 =

Repeat until convergence

\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_1^i)
1m∑i=1m((h(xi)−yi)x1i)\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_1^i)
\theta_1
θ1\theta_1
-\alpha
−α-\alpha
\theta_1 =
θ1=\theta_1 =
\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_2^i)
1m∑i=1m((h(xi)−yi)x2i)\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_2^i)
\theta_2
θ2\theta_2
-\alpha
−α-\alpha
\theta_2 =
θ2=\theta_2 =
\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_n^i)
1m∑i=1m((h(xi)−yi)xni)\frac{1}{m}\sum_{i=1}^{m}(({h (x^i) - y^i})x_n^i)
\theta_n
θn\theta_n
-\alpha
−α-\alpha
\theta_n =
θn=\theta_n =

Multiple Variables

We can rewrite this as 

\hat{y} = \theta^Tx
y^=θTx\hat{y} = \theta^Tx

Predicted

Output

Parameters

Vector

Input

Vector

(how did we get here?)

h(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3
h(x)=θ0+θ1x1+θ2x2+θ3x3h(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3

Adjusting the names

\hat{y} = w^Tx
y^=wTx\hat{y} = w^Tx

Recap

  • Hypothesis h
  • Cost function: the difference between our hypothesis and the output in the training set
  • Gradient descent: minimizes the difference

Don't forget this :)

Problem

h(x) = \theta_0 + \theta_1x
h(x)=θ0+θ1xh(x) = \theta_0 + \theta_1x

Problem

h(x) = \theta_0 + \theta_1x
h(x)=θ0+θ1xh(x) = \theta_0 + \theta_1x

Does it look good?

Underfitting

h(x) = \theta_0 + \theta_1x
h(x)=θ0+θ1xh(x) = \theta_0 + \theta_1x

The predicted output is not even fitting the training data!

Problem

h(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4
h(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4h(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4

Does it look good?

Overfitting

h(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4
h(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4h(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4

The model fits everything

[Over, Under]fitting were problems related to the capacity

Capacity: Ability to fit a wide variety of functions

Overfitting

Underfitting

How can we control the capacity?

a) change the number of input features

b) change the parameters associated with the features

By controlling the capacity, we are searching for an ideal model

It is difficult to know the true probability distribution that generates the data, so we want the lowest possible error rate (Bayes error)

Problem

The training set works fine; new predictions are terrible

The problem might be the cost function (comparing the predicted values with the training set)

-

h(x^i)
h(xi)h(x^i)
y^i
yiy^i
\sum_{i=1}^{m}
∑i=1m\sum_{i=1}^{m}
)^2
)2)^2
(
((
\frac{1}{2m}
12m\frac{1}{2m}

J =

A better cost function

-

h(x^i)
h(xi)h(x^i)
y^i
yiy^i
\sum_{i=1}^{m}
∑i=1m\sum_{i=1}^{m}
)^2
)2)^2
(
((
\frac{1}{2m}
12m\frac{1}{2m}

J =

[
[[
+ \lambda
+λ+ \lambda
\sum_{j=1}^{numfeat} \theta_j^2
∑j=1numfeatθj2\sum_{j=1}^{numfeat} \theta_j^2
]
]]

Regularization param

It controls the tradeoff / lowers the variance

c) Regularization

(another mechanism to control the capacity)

d) Hyperparameters - parameters that control parameters

Select setting that the algorithms can't learn to be hyperparameters

Question: If we use the entire dataset to train the model, how do we know if it's [under,over]fitting?

Your Dataset

Training set

Learn the parameter θ; compute J(θ) 

Test set

Compute the test set error (identify [under,over]fitting)

70%

30%

(cross-validation)

We can analyze the relations between the errors on the training and test sets

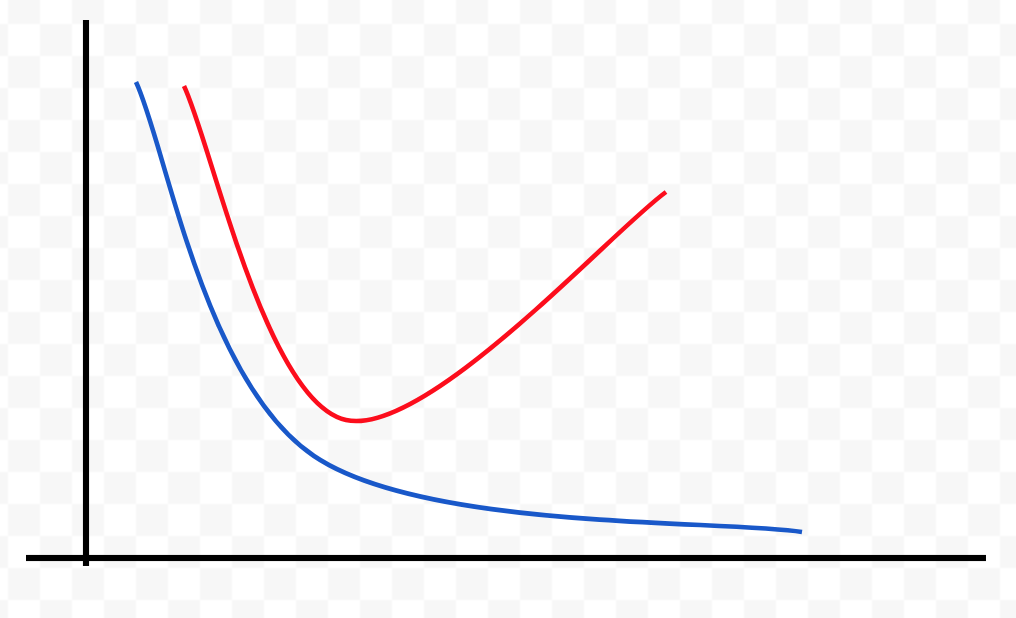
Error

Capacity

J(θ) test error

J(θ) train error

Error

Capacity

J(θ) test error

J(θ) train error

Bias problem (underfitting)

J(θ) train error is high

J(θ) train ≈ J(θ) test

J(θ) train error is low

J(θ) test >> J(θ) train

Variance problem (overfitting)

Bias - measures the expected deviation from the true value of the function or parameter

Variance - measures the deviation from the expected estimator value that any sampling can cause

How do we select good estimators?

A: Maximum likelihood estimation or Bayesian statistics

WE MADE IT TO THE END OF THIS SESSION!

(Not yet!)

How do I transform all this into code???

Octave/ Matlab for prototyping

Adjust your theory to work with Linear Algebra and Matrices

 

Expand the derivatives:

\frac{1}{m}\sum_{i=1}^{m}(({h (x_i) - y_i}) x_i)
1m∑i=1m((h(xi)−yi)xi)\frac{1}{m}\sum_{i=1}^{m}(({h (x_i) - y_i}) x_i)
\frac{1}{m}\sum_{i=1}^{m}({h (x_i) - y_i})
1m∑i=1m(h(xi)−yi)\frac{1}{m}\sum_{i=1}^{m}({h (x_i) - y_i})
a_0
a0a_0
b_0
b0b_0
-\alpha
−α-\alpha
-\alpha
−α-\alpha
a =
a=a =
b =
b=b =

Repeat until convergence

The dataset:

 source: https://github.com/stedy/Machine-Learning-with-R-datasets/blob/master/usedcars.csv

 

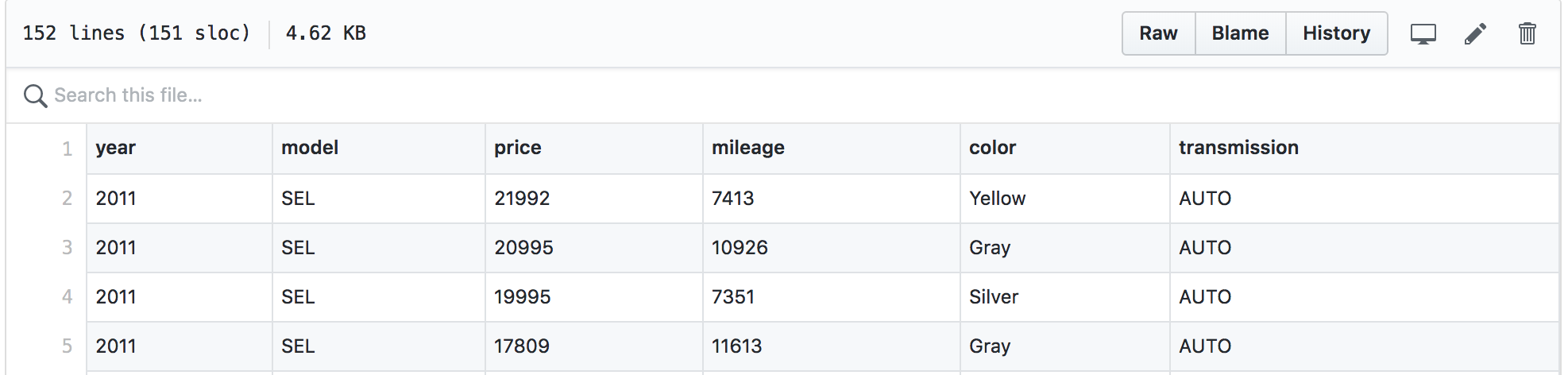
The code in Octave

data = load('used_cars.csv'); %year x price
y = data(:, 2);
X = [ones(m, 1), data(:,1)];
theta = zeros(2, 1); %linear function
iterations = 1500;
alpha = 0.01;
m = length(y);
J = 0;

predictions = X*theta;

sqErrors = (predictions - y).^2;
J = 1/(2*m) * sum(sqErrors);

J_history = zeros(iterations, 1);

for iter = 1:iterations
    x = X(:,2);
    delta = theta(1) + (theta(2)*x);
    tz = theta(1) - alpha * (1/m) * sum(delta-y);
    t1 = theta(2) - alpha * (1/m) * sum((delta - y) .* x);
    theta = [tz; t1];
    J_history(iter) = computeCost(X, y, theta);
end

Initialise

Cost

Function

Gradient

Descent

In a large project

Linear regression with C++

mlpack

mlpack_linear_regression --training_file used_cars.csv
 --test_file used_cars_test.csv -v

Bonus!

References

GIF time

Thank you :)

Questions?

 

gustavoergalves@gmail.com

 

hannelita@gmail.com

@hannelita