Profunctor Optics
Overview
- Algebraic Data Types
- Lens Library
- Functors
- Profunctor Optics
lens
type Iso' s a =
forall p f. (Profunctor p, Functor f) => p a (f a) -> p s (f s)
type Lens' s a =
forall f. (Functor f) => (a -> f a) -> s -> f s
type Prism' s a =
forall p f. (Choice p, Applicative f) => p a (f a) -> p s (f s)
type Traversal' s a =
forall f. (Applicative f) => (a -> f a) -> s -> f s
type Fold s a =
forall p f. (Contravariant f, Applicative f) => a (f a) -> s -> f spurescript-profunctor-lenses
type IsoP s a =
forall p. (Profunctor p) => p a a -> p s s
type LensP s a =
forall p. (Strong p) => p a a -> p s s
type PrismP s a =
forall p. (Choice p) => p a a -> p s s
type TraversalP s a =
forall p. (Wander p) => p a a -> p s s
type FoldP r s a =
Forget r a a -> Forget r s sAlgebraic Data Types
to the code...
Sum Types
data IorB = I Int | B BoolSum Types
data IorB = I Int | B Bool
type IorB' = Either Int Bool
-- `IorB <~> Either Int Bool`
-- IorB -> IorB'
matchIorB :: IorB -> Either Int Bool
matchIorB (I n) = Left n
matchIorB (B b) = Right b
-- IorB' -> IorB
injectIorB :: Either Int Bool -> IorB
injectIorB (Left n) = (I n)
injectIorB (Right b) = (B b)Are isomorphic to Either
Sum Types
data IorB = I Int | B Bool
-- Sum examples
five :: IorB
five = I 5
truuu :: IorB
truuu = B TrueValues of the Day:
Product Types
data Person = P
{ _pName :: String
, _pAge :: Int
}
data AlsoPerson = AP String IntProduct Types
-- | `P String Int <~> (String, Int)`
type Person = (String,Int)
-- | Person -> Person'
splitP :: Person -> (String, Int)
splitP (P name age) = (name, age)
-- | Person' -> Person
unsplitP :: (String, Int) -> Person
unsplitP (name, age) = P name ageProduct Types
data Person = P
{ _pName :: String
, _pAge :: Int
}
-- Values
john :: Person
john = P "John" 889
sue :: Person
sue = P "Sue" 407Values of the Day:
Lens Library
Lens Library
- Lenses
- Prisms
- Isos
- Traversals
- Folds
Lens Library
Challenge:
Given a list of homeowners, modify each homeowner's address by capitalizing each address' street name:
Lens Library
// Java
for (Homeowner owner : ArrayList<HomeOwner>) {
person.address.street.name.toUpper()
}-- Haskell
fmap updateHomeOwner homeowners
where updateHomeOwner (HomeOwner name age address)
= HomeOwner name age (updateAddress address)
updateAddress (Address (Street no name) state zip))
= Address (Street no (toUpper name)) state zipLens Library
-- Haskell
over (traverse.address.street.name) toUpper homeowners// Java
for (Homeowner owner : ArrayList<HomeOwner>) {
person.address.street.name.toUpper()
}Lens Library
λ> view pName john
"John"
λ> view pName sue
"Sue"
λ> view pAge john
889
λ> view pAge sue
407
λ> set pAge 10 sue
P {_pName = "Sue", _pAge = 10}
λ> set pName "Sue" john
P {_pName = "Sue", _pAge = 889}
λ> over pAge (+111) john
P {_pName = "Sue", _pAge = 889}
Person lenses pName and pAge
john :: Person
john = P "John" 889
sue :: Person
sue = P "Sue" 407pName :: Lens' Person String
pAge :: Lens' Person IntLens Library
λ> preview _I five
Just 5
λ> preview _B five
Nothing
λ> preview _I truuu
Nothing
λ> preview _B truuu
Just True
λ> review _B True
B True
λ> review _I 5
I 5
λ> over _I (+95) five
I 100IorB prisms _I and _B
five :: IorB
five = I 5
truuu :: IorB
truuu = B True_I :: Prism' IorB Int
_B :: Prism' IorB BoolFunctors
Functor
(Covariant)
class Functor f where
fmap :: (a -> b) -> f a -> f ba
b
a -> b
F
F
Functor
class Functor f where
fmap :: (a -> b) -> f a -> f b-- | `[x] = [] x` where f=`[]` and a=`x`
λ> fmap (+10) [1,2,3,4]
[11,12,13,14]
-- | `(x,y) = (,) x y` where f=`(x,)` and a=`y`
λ> fmap (+10) (1,2)
(1,12)
-- | `data Either x y = Left x | Right y` where
-- | f=`Either x` and a=`y`
λ> fmap (+10) (Left 1)
Left 1
λ> fmap (+10) (Right 2)
Right 12Bifunctor
class Bifunctor p where
bimap :: (a -> b) -> (c -> d) -> p a c -> p b da -> b
a
c
b
d
P
P
c -> d
-- | `(x,y) = (,) x y` where f=`(,)` and
-- | a=`x` and b=`y`
λ> bimap (+10) (+50) (1,1)
(11,51)
-- | `data Either x y = Left x | Right y` where
-- | f=`Either` a=`x` and b=`y`
λ> bimap (+10) (+50) (Left 1)
Left 11
λ> bimap (+10) (+50) (Right 1)
Right 51Bifunctor
class Bifunctor p where
bimap :: (a -> b) -> (c -> d) -> p a c -> p b dContravariant Functor
class Contravariant f where
contramap :: (a -> b) -> f b -> f ab
a -> b
F
Contravariant Functor
class Contravariant f where
contramap :: (a -> b) -> f b -> f aa -> b
b
F
a
F
Profunctor
class Profunctor p where
dimap :: (a -> b) -> (c -> d) -> p b c -> p a d
lmap :: (a -> b) -> p b c -> p a c
rmap :: (b -> c) -> p a b -> p a ca -> b
b
c
P
c -> d
Profunctor
class Profunctor p where
dimap :: (a -> b) -> (c -> d) -> p b c -> p a d
lmap :: (a -> b) -> p b c -> p a c
rmap :: (b -> c) -> p a b -> p a ca -> b
b
c
P
c -> d
Profunctor takes a "pre-computation", a "post-computation", and an intermediate relationship between
between things
Profunctor
class Profunctor p where
dimap :: (a -> b) -> (c -> d) -> p b c -> p a d
lmap :: (a -> b) -> p b c -> p a c
rmap :: (b -> c) -> p a b -> p a ca -> b
b
c
P
c -> d
a
d
P
Strong Profunctor
-- | The "operate on a part of a whole" typeclass
class Profunctor p => Strong p where
first' :: p a b -> p (a, q) (b, q)Think of the following:
• p a b as a relationship on a part
• p (a,q) (b,q) as a relationship on the whole
Strong Profunctor
-- | The "operate on a part of a whole" typeclass
class Profunctor p => Strong p where
first' :: p a b -> p (a, q) (b, q)a
b
P
(a,q)
(b,q)
P
Choice Profunctor
-- | The "operate on a branch of a
-- | possibility" typeclass
class Profunctor p => Choice p where
left' :: p a b -> p (Either a q) (Either b q)Think of the following:
• p a b as a relationship on a branch
• p (Either a q) (Either b q) as a relationship on all possibilities
Choice Profunctor
-- | The "operate on a branch of a
-- | possibility" typeclass
class Profunctor p => Choice p where
left' :: p a b -> p (Either a q) (Either b q)a
b
P
Either a q
P
Either b q
to the code...
Profunctor Optics
Profunctor Optics
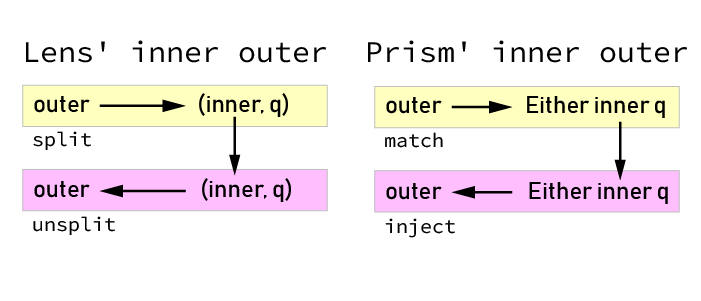
Simple Optics
Lens' inner outer and Prism' inner outer isomorphisms
https://blog.jle.im/entry/lenses-products-prisms-sums.html
Profunctor Optics
Lens Families
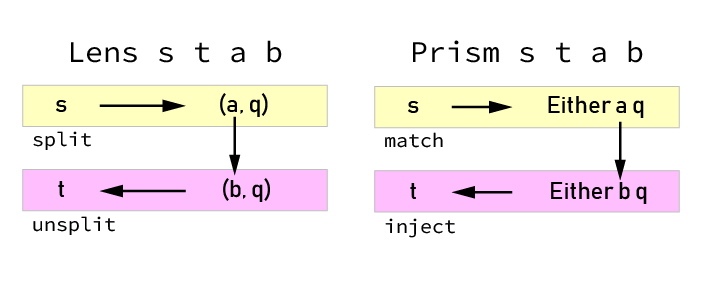
Lens s t a b and Prism s t a b isomorphisms, as a lens family
https://blog.jle.im/entry/lenses-products-prisms-sums.html
purescript-profunctor-lenses
type IsoP s a =
forall p. (Profunctor p) => p a a -> p s s
type LensP s a =
forall p. (Strong p) => p a a -> p s s
type PrismP s a =
forall p. (Choice p) => p a a -> p s s
-- class (Strong p, Choice p) => Wander p where..
type TraversalP s a =
forall p. (Wander p) => p a a -> p s s
type FoldP r s a =
Forget r a a -> Forget r s sProfunctor Optics
type Optic c s t a b = forall p. c p => p a b -> p s t
type Optic c s t a b = forall p. c p => p a b -> p s tC =
Strong
Traversing1
Choice
Bicontravariant
Bifunctor
Mapping
http://oleg.fi/gists/posts/2017-04-18-glassery.html
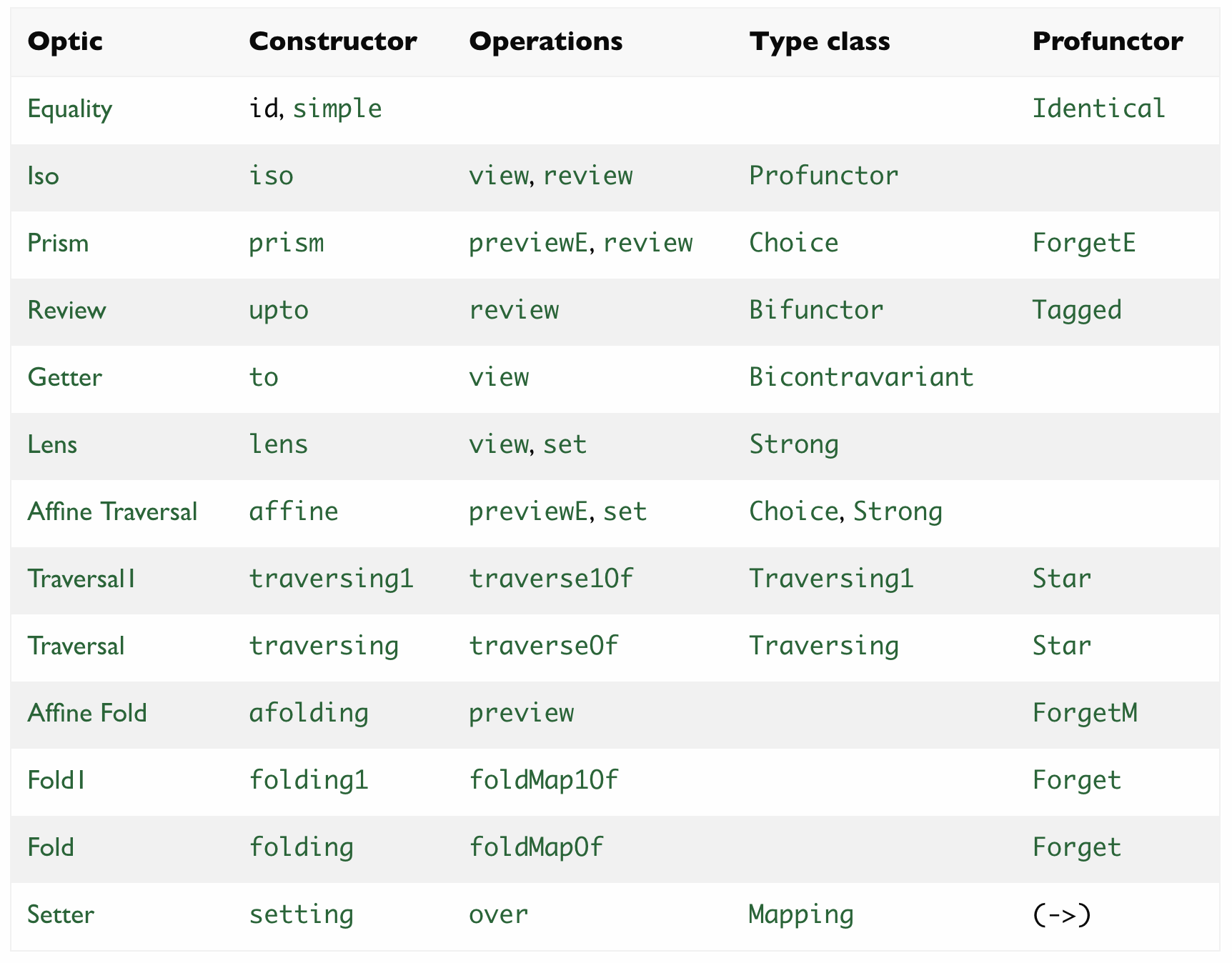
http://oleg.fi/gists/posts/2017-04-18-glassery.html