Type Level Programming

In Haskell

Plan

What is Type Level Programming?
Syntax Primer
Algebra of Types
Kind System
GADTs
Type Families
Rank Polymorphism
Type Variables
- Scope and Application
First Class Families
- Defuntionalization

What am I skipping?

Existentials
- Eliminators
- ST Trick
  - Rigid Skolems
Servant
- What and How?
- Why?
  - Expression Problem
Data Families
- vs GADTs
Role System
Scalar operations on higher ranked data

Typical Haskell

Terms
- the values you can manipulate
- exist at runtime
- inhabit some type
Types
- proofs to the compiler (and ourselves) that the programs we’re trying to write make some amount of sense (aka typechecks)

isOdd :: Int -> Bool
isOdd n = False

Type-Level Haskell

Types
- the values you can manipulate
- exist at compile time
- inhabit some kind
Kinds
- proofs to the compiler (and ourselves) that the programs we’re trying to write make some amount of sense (aka kindchecks)

type family IsOdd (n :: GHC.TypeLits.Nat) :: Bool where
  IsOdd n = 'False

Kinds

Kind system
- “the type system for types”
Kinds
- “the types of types”

{-# LANGUAGE UndecidableInstances, KitchenSink #-}

import Fcf          -- (=<<), Eval, Not, TyEq
import GHC.TypeLits -- Mod, Nat(0..)

------------------------------------
-- Term Level

isOdd :: Int -> Bool
isOdd n = (mod n 2) /= 0
-- λ> isOdd 11
-- True

------------------------------------
-- Type Level

type family IsOdd (n :: Nat) :: Bool where
  IsOdd n = Eval (Not =<< (TyEq (Mod n 2) (0)))
-- λ> :kind! IsOdd 10
-- IsOdd 11 :: Bool
-- = 'True

Type Level Programming

Constructing programs which execute at compile time taking types as input and return as output both new types and runtime functionality

Beware!

Haskell Primer

Data Types

data Bool = True | False

data [a]  = [] | a : [a]

filter :: (a -> Bool) -> [a] -> [a]
filter pred []     = []
filter pred (x:xs) = 
  case pred x of
    False -> x : filter pred xs
    True  -> filter pred xs

Functions

Data Types

data Bool = True | False

data [a]  = [] | a : [a]

data Three a b c = Three a b c

false = False :: Bool

fives = [5,5,5,5,5] :: [Int]

three = Three 10 (-10) 9001 :: Three Int Int Int

Declare new data types with data

Data Types

data Bool = True | False

data [a]  = [] | a : [a]

data Three a b c = Three a b c

false = False :: Bool

fives = [5,5,5,5,5] :: [Int]

three = Three 10 (-10) 9001 :: Three Int Int Int

Type Constructor

Data Constructor

filter :: (a -> Bool) -> [a] -> [a]
filter pred []     = []
filter pred (x:xs) = 
  case pred x of
    False -> x : filter pred xs
    True  -> filter pred xs

Functions

filter :: (a -> Bool) -> [a] -> [a]
filter pred []     = []
filter pred (x:xs) = 
  case pred x of
    False -> x : filter pred xs
    True  -> filter pred xs

Functions

Type Signature

filter :: (a -> Bool) -> [a] -> [a]
filter pred []     = []
filter pred (x:xs) = 
  case pred x of
    False -> x : filter pred xs
    True  -> filter pred xs

Functions

Parametric Polymorphism

filter :: (a -> Bool) -> [a] -> [a]
filter pred []     = []
filter pred (x:xs) = 
  case pred x of
    False -> x : filter pred xs
    True  -> filter pred xs

Functions

Higher Order Function

filter :: (a -> Bool) -> [a] -> [a]
filter pred []     = []
filter pred (x:xs) = 
  case pred x of
    False -> x : filter pred xs
    True  -> filter pred xs

Functions

Patterns

class  Num a  where
  (+) :: a -> a -> a
  (-) :: a -> a -> a
  (*) :: a -> a -> a

Classes and Instances

instance Num Int where
  (+) :: Int -> Int -> Int
  a + b = plusInt a b

  (-) :: Int -> Int -> Int
  a - b = minusInt a b

  (*) :: Int -> Int -> Int
  a * b = timesInt a b

square :: Num a => a -> a
square x = x * x

class  Num a  where
  (+) :: a -> a -> a
  (-) :: a -> a -> a
  (*) :: a -> a -> a

Classes and Instances

instance Num Int where
  (+) :: Int -> Int -> Int
  a + b = plusInt a b

  (-) :: Int -> Int -> Int
  a - b = minusInt a b

  (*) :: Int -> Int -> Int
  a * b = timesInt a b

square :: Num a => a -> a
square x = x * x

Context / Constraint

Ad Hoc Polymorphism

Algebra of Types

Algebra behind ADTs

Cardinality — the number of inhabitants in a type (ignoring bottoms)

data Void

data () = ()

data Bool = False | True

data Alphabet a c = Alphabet a Bool c

data Maybe a = Nothing | Just a

Algebra behind ADTs

-- 0
data Void

-- 1
data () = ()


-- 1 + 1 = 2
data Bool = False | True

-- |a| * 2 * |c|
data Alpha a c = Alphabet a Bool c

-- 1 + |a|
data Maybe a = Nothing | Just a

|Void| = 0

|()| = 1

|Bool|= 2

|Alpha Bool Bool| = 8

|Maybe ()| = 2

Isomorphism

Any two types that have the same cardinality will always be isomorphic to one another.

An isomorphism between types s and t is deﬁned as a pair of functions to and from such that composing either after the other gets you back where you started.

s t

to :: s -> t
to = _
from :: t -> s
from = _

to . from = id
from . to = id

Isomorphism

s t

data S = S deriving Show
data T = T deriving Show

λ> (toT . fromT) T
T
λ> (fromT . toT) S
S

toT :: S -> T
toT S = T

fromT :: T -> S
fromT T = S

Isomorphism

s t

data S = S deriving Show
data T = T deriving Show

λ> (fromT . toT) S
S
λ> (toT . fromT) T
T

toT :: S -> T
toT S = T

fromT :: T -> S
fromT T = S

toS :: T -> S
toS T = S

fromS :: S -> T
fromS S = T

λ> (fromS . toS) T
T
λ> (toS . fromS) S
S

Identity

() as multiplicative identity
- |()| = 1
- a * 1 = a

prodUnitTo :: a -> (a, ())
prodUnitTo a = (a, ())

prodUnitFrom :: (a, ()) -> a
prodUnitFrom (a, ()) = a

Void as additive identity
- |Void| = 0
- a + 0 = a

sumUnitTo :: Either a Void -> a
sumUnitTo (Left a) = a
sumUnitTo (Right v) = absurd v


sumUnitFrom :: a -> Either a Void
sumUnitFrom = Left

Cardinality of (->)

Function types correspond to exponentiation

|a -> b| = |b| × |b| × · · · × |b| = |b|^|a|

Basically states that for every value in a, there is a mapping to any value in b

Cardinality of (->)

id :: Bool -> Bool
id b = b

not :: Bool -> Bool
not = \case
    False -> True
    True  -> False

constTrue :: Bool -> Bool
constTrue = const True

constFalse :: Bool -> Bool
constFalse = const False

|Bool -> Bool| = |Bool| * |Bool| = |2| ^ |2| = 4

Function types correspond to exponentiation

Curry-Howard Isomorphism

Algebra	Logic	Types
a + b	a ∨ b	Either a b
a × b	a ∧ b	(a, b)
b ^ a	a ⇒ b	a -> b
a = b	a ⇐⇒ b	isomorphism
0	⊥	Void
1	⊤	()

Every statement in logic is equivalent to some computer program, and vice versa

Insights from Curry-Howard Isomorphism

Consider a^1 = a
- () -> a is isomorphic to a
  - Means that there is no distinction between having a value and having a (pure) program that computes that value

Canonical Representations

A direct corollary that any two types with the same cardinality are isomorphic, is that there are multiple ways to represent any given type.

This canonical representation is known as a sum of products, and refers to any type t of the form

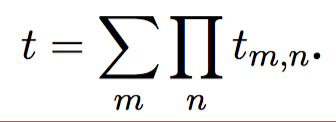
Kind System

{#- LANGUAGE PolyKinds -#}
{#- LANGUAGE KindSignatures -#}
{#- LANGUAGE DataKinds -#}

Kinds

Kind system
- “the type system for types”
Kinds
- “the types of types”

Constraint Kinds

Constraint is the kind of any fully saturated typeclass

{#- LANGUAGE ConstraintKinds -#}

show :: Show a => a -> String

Show has kind Type -> Constraint
Show Int has kind Constraint

ConstraintKinds lets you to declare a tuple of constraints as a type synonym

type ReadShow a = (Read a, Show a)

PolyKinds

Introduce a kind k which can be higher-kinded
Proxy is poly-kinded, so Proxy anything will have kind Type
- Proxy Char where k is Type.
- Proxy (,) where k is Type -> Type
- Proxy Show where k is Type -> Constraint
- Proxy Monad where k is (Type -> Type) -> Constraint

{#- LANGUAGE PolyKinds -#}

DataKinds

Datatype Promotion
- The “promotion” of fully applied type constructors to kinds, and the promotion of certain data constructors to types

{#- LANGUAGE DataKinds -#}

data Bool = False | True

-- Produces kind `Bool` and types `'True` and `'False`
-- λ> :k 'True
-- 'True :: Bool
-- λ> :k 'False
-- 'False :: Bool

GADTs

{#- LANGUAGE GADTs -#}

Type Equality

Type Equality
- Constraint that two types are equal
- Form an equivalence relation
  - Reflexivity - a type is equal to itself a ~ a
  - Symmetry - a ~ b iff b ~ a
  - Transitivity - if a ~ b and b ~ c, then a ~ c
five and five_ are equivalent

five :: Int
five = 5

five_ :: (a ∼ Int) => a
five_ = 5

{#- LANGUAGE GADTs -#}

GADTS

Generalized Algebraic Data Types
Allow explicit type signatures to be written for data constructors

data Maybe a where
  Nothing :: Maybe a
  Just    :: a -> Maybe a

just5 = Just 5

data HList (xs :: [*]) where
    HNil :: HList '[]
    (:#) :: a -> HList as -> HList (a ': as)

infixr 5 :#

things :: HList '[Bool, Int, Int]
things = True :# 0 :# 10 :# HNil

GADTS

data HList (xs :: [*]) where
    HNil :: HList '[]
    (:#) :: a -> HList as -> HList (a ': as)

infixr 5 :#

things :: HList '[Bool, Int, Int]
things = True :# 0 :# 10 :# HNil

instance Show (HList '[]) where
  show HNil = "HNil"

instance (Show t, Show (HList ts))
      => Show (HList (t ': ts)) where
  show (a :# as) = show a <> " :' " <> show as

-- λ> show things
-- "True :' 0 :' 10 :' HNil"

Common Pattern - Inductive definitions

GADTS

Type Safe Syntax Tree

{#- LANGUAGE GADTs -#}

data Expr a where
  LitInt  :: Int -> Expr Int
  LitBool :: Bool -> Expr Bool
  Add     :: Expr Int -> Expr Int -> Expr Int
  Not     :: Expr Bool -> Expr Bool
  If      :: Expr Bool -> Expr a -> Expr a -> Expr a

evalExpr :: Expr a -> a
evalExpr (LitInt i) = i
evalExpr (LitBool b) = b
evalExpr (Add x y) = evalExpr x + evalExpr y
evalExpr (Not x) = not $ evalExpr x
evalExpr (If b x y) =
  if evalExpr b then evalExpr x else evalExpr y

-- λ> evalExpr $ If (LitBool False)
--                  (LitInt 1) (Add (LitInt 5) (LitInt 1))
-- 6
-- λ> evalExpr . Not $ LitBool True
-- False

GADTS

GADTs are just syntactic sugar over type equalities

{#- LANGUAGE GADTs -#}

data Expr a where
  LitInt  :: Int -> Expr Int
  LitBool :: Bool -> Expr Bool
  Add     :: Expr Int -> Expr Int -> Expr Int
  Not     :: Expr Bool -> Expr Bool
  If      :: Expr Bool -> Expr a -> Expr a -> Expr a

data Expr_ a =
    (a ∼ Int)  => LitInt_ Int
  | (a ∼ Bool) => LitBool_ Bool
  | (a ∼ Int)  => Add_ (Expr_ Int) (Expr_ Int)
  | (a ∼ Bool) => Not_ (Expr_ Bool)
  | If_ (Expr_ Bool) (Expr_ a) (Expr_ a)

Type Families

{#- LANGUAGE TypeFamilies -#}

Closed Type Families

We can manually “promote” term-level functions by writing a closed type family
- Can't automatically promote term-level functions into type-level ones (like data constructors)
- Explicitly duplicate term level logic

or :: Bool -> Bool -> Bool
or True _ = True
or False y = y

type family Or (x :: Bool) (y :: Bool) :: Bool where
  Or 'True y = 'True
  Or 'False y = y

Open Type Families

Like closed type families but you can keep adding type instances

or :: Bool -> Bool -> Bool
or True _ = True
or False y = y

type family Or (x :: Bool) (y :: Bool) :: Bool
type instance Or 'True  y = 'True
type instance Or 'False y = y

Saturation

Type families must be fully "saturated"
- No type-level currying
  - AKA no partial application
We can write a type level Map compiles but we can't use it

type family Map (x :: a -> b) (i :: [a]) :: [b] where
  Map f '[] = '[]
  Map f (x ': xs) = f x ': Map f xs

-- λ> :t undefined :: Proxy (Map (Or 'True)
--                    '[ 'True, 'False , 'False ])
-- <interactive>:1:14: error:
--    • The type family ‘Or’ should have 2 arguments,
--      but has been given 1....

Associated Type Families

Type families associated with a typeclass
- Because typeclasses are our means of providing ad-hoc polymorphism, associated type families allow us to compute ad-hoc types.
Associated type families are always open

class Collection c where
  type Elem c :: *
  firstElem :: c -> Elem c

instance Collection [a] where
  type Elem [a] = a
  firstElem (x:xs) = x

instance Collection (a,b) where
  type Elem (a,b) = a
  firstElem (x,y) = x

Associated Type Families

The type indexes corresponding to class parameters must be identical to the type given in the instance head
If an associated family instance is omitted, the corresponding instance type is not inhabited

class Collection c where
  type Elem c :: *
  firstElem :: c -> Elem c

instance Collection [a] where
  type Elem [a] = a
  firstElem (x:xs) = x

instance Collection (a,b) where
  firstElem _ = undefined
-- <interactive>:614:1: warning: [-Wmissing-methods]
--    • No explicit associated type or default...

Type Variables

Scope and Application

Visible Type Applications

Like type annotations but better
An argument of the form @ty specifies a type argument
- You can avoid applying a type with an underscore
- Types are applied in the same order they appear in a type signature (including context and forall quantifiers)

λ> :t fmap
fmap :: Functor f => (a -> b) -> f a -> f b
λ> :t fmap @_ @Int @Bool
fmap @_ @Int @Bool :: Functor w => (Int -> Bool)
                                -> w Int
                                -> w Bool

{#- LANGUAGE TypeApplications -#}

This compiles :)

prefix :: a -> [[a]] -> [[a]]
prefix x yss = map xcons yss
  where xcons ys = x : ys

This doesn't compile!! Why?

prefix :: a -> [[a]] -> [[a]]
prefix x yss = map xcons yss
  where xcons :: [a] -> [a]
        xcons ys = x : ys

Fixed!

{-# LANGUAGE ScopedTypeVariables #-}

prefix :: forall a. a -> [[a]] -> [[a]]
prefix x yss = map xcons yss
  where xcons :: [a] -> [a]
        xcons ys = x : ys

Scoped Type Variables

Provides lexically scoped type variables
- Quantifies a for everything "under" prefix

{#- LANGUAGE ScopedTypeVariables -#}

{-# LANGUAGE ScopedTypeVariables #-}

prefix :: forall a. a -> [[a]] -> [[a]]
prefix x yss = map xcons yss
  where xcons :: [a] -> [a]
        xcons ys = x : ys

Need for Type Annotations

Machine-checked documentation
As Haskell’s type system becomes increasingly expressive, complete type inference becomes intractable
- type system necessarily relies on programmer-supplied type annotations.

Type-class ambiguity

normalize :: String -> String
normalize s = show (read s)

normalize s = show (read s :: Int)

Doesn't compile

COMPILES!!!!!!!!!!!!!!!!!!!!!!

λ> :t read
read :: Read a => String -> a
λ> :t show
show :: Show a => a -> String
λ> :t show . read
show . read :: String -> String

Consider:

Polymorphic Recursion

data T a = Leaf a | Node (T [a]) (T [a])

leaves :: T a -> [a]
leaves (Leaf x) = [x]
leaves (Node t1 t2) = concat (leaves t1 ++ leaves t2)

-- λ> leaves (Leaf x) = [x]
-- λ> leaves (Node t1 t2) = concat (leaves t1 ++ leaves t2)
--
-- <interactive>:152:1: error:
--     • Occurs check: cannot construct the infinite type: a ~ [a]
--       Expected type: T [a] -> [[a1]]
--         Actual type: T a -> [a1]
--     • Relevant bindings include
--         leaves :: T [a] -> [[a1]] (bound at <interactive>:152:1)

Type inference for polymorphic recursion is undecidable and requires programmer supplied type annotations

GADTS

data G a where
  MkInt :: G Int
  MkFun :: G (Int -> Int)

matchG :: G a -> a
matchG MkInt = 5
matchG MkFun = (+10)

matchG won't type-check without type signature
When we learn that a value g :: G a is actually the constructor MkInt, then we simultaneously learn that a really is Int

Ambiguous Types

type family F a
type instance F Bool = Char

ambig :: Typeable a => F a -> Int
ambig _ = 5

test :: Char -> Int
test x = ambig @Bool x

In test, GHC must decide what type should instantiate the a in ambig’s type. Any choice a = τ must ensure that F τ ∼ Char but, because F might not be injective, that does not tell us what a should be.
A type signature isn't enough, we need TypeApplications

Rank Polymorphism

{#- LANGUAGE RankNTypes -#}

Rank Polymorphism

Example

applyToFive :: (a -> a) -> Int
applyToFive f = f 5

-- <interactive>:650:17: error:
--     • Couldn't match expected type
--       ‘Int’ with actual type ‘a’

Won't compile :(

applyToFive :: (forall a. a -> a) -> Int
applyToFive f = f 5

-- λ> applyToFive id
-- 5

Compiles! :)

Rank Polymorphism

Rank
- the rank of a function is the “depth” of its polymorphism
  - A function that has no polymorphic parameters is rank 0
  - Most common functions are rank 1
  - any function above rank-1 to be rank-n or higher rank
Rank Polymorphism
- Makes polymorphism first class
- In general, type inference is undecidable in the presence of higher-rank polymorphism
  - higher-rank polymorphism always requires an explicit type signature.

Rank Polymorphism

Higher-rank types
- functions which take callbacks.
The rank of a function is how often control gets “handed off”
- A rank-2 function will call a polymorphic function for you
- A rank-3 function will run a callback which itself runs a callback

Rank Polymorphism

Consider:

foo :: forall r. (forall a. a -> r) -> r
foo fn = _

We get to determine the return type r, but we never get implementation of whatever fn is get to decide what a is

Counting Rank

The rank of a function is simply the number of arrows its deepest forall is to the left of
The forall quantiﬁer binds more loosely than the arrow type (->), so forall a. a -> a is forall a. (a -> a)

What are the ranks of foo, bar, and baz?

foo :: Int -> forall a. a -> a             

bar :: (a -> b) -> (forall c. c -> a) -> b

baz :: ((forall x. m x -> b (z m x))      
    -> b (z m a))
    -> m a

Counting Rank

The rank of a function is simply the number of arrows its deepest forall is to the left of
The forall quantiﬁer binds more loosely than the arrow type (->), so forall a. a -> a is forall a. (a -> a)

foo :: Int -> forall a. a -> a             -- rank 1

bar :: (a -> b) -> (forall c. c -> a) -> b -- rank-2

baz :: ((forall x. m x -> b (z m x))       -- rank-3
    -> b (z m a))
    -> m a

First Class Families

Defunctionalization

the process of replacing an instantiation of a polymorphic function with a specialized label instead

fst :: (a, b) -> a
fst (a, b) = a

-- Defunctionalized
data Fst a b = Fst (a, b)

class Eval l t | l -> t where
  eval :: l -> t

instance Eval (Fst a b) a where
  eval (Fst (a, b)) = a

-- λ> eval $ Fst (10,20)
-- 10

Defunctionalizing Higher Order Functions

type family Map (x :: a -> b) (i :: [a]) :: [b] where
  Map f '[] = '[]
  Map f (x ': xs) = f x ': Map f xs

Type-Level Defunctionalization

type Exp a = a -> Type

type family Eval (e :: Exp a) :: a

data Snd :: (a, b) -> Exp b
type instance Eval (Snd '(a, b)) = b

-- λ> :kind! Eval (Snd '(1, " hello " ))
-- Eval (Snd '(1, " hello " )) :: Symbol
-- = " hello "

-------------------------------------------
-- Term Level 

data Optional a = Missing | Present a

fromOptional :: a -> Optional a -> a
fromOptional deflt Missing     = deflt
fromOptional deflt (Present a) = a

-------------------------------------------
-- Type Level

import qualified GHC.TypeLits as TL

data FromOptional :: k -> Optional k -> Exp k
type instance Eval (FromOptional a  'Missing)     = a
type instance Eval (FromOptional _a ('Present b)) = b

data Plus :: TL.Nat -> TL.Nat -> Exp TL.Nat
type instance Eval (Plus a b) = a TL.+ b

-------------------------------------------
-- Term Level 

data Optional a = Missing | Present a

fromOptional :: a -> Optional a -> a
fromOptional deflt Missing     = deflt
fromOptional deflt (Present a) = a

-------------------------------------------
-- Type Level

import qualified GHC.TypeLits as TL

data FromOptional :: k -> Optional k -> Exp k
type instance Eval (FromOptional a  'Missing)     = a
type instance Eval (FromOptional _a ('Present b)) = b

data Plus :: TL.Nat -> TL.Nat -> Exp TL.Nat
type instance Eval (Plus a b) = a TL.+ b

Higher Order Type Functions

data Optional a = Missing | Present a

data FromOptional :: k -> Optional k -> Exp k
type instance Eval (FromOptional a  'Missing)     = a
type instance Eval (FromOptional _a ('Present b)) = b

-- λ> :kind! Eval (Map (FromOptional 3)
--                [ 'Present 1, 'Present 2, 'Missing])
-- Eval (Map (FromOptional 3)
--      [ 'Present 1, 'Present 2, 'Missing]) :: [GHC.Types.Nat]
-- = '[1, 2, 3]

While you can't use Type Families with partially applied types, you can use type level defunctionalization

First Class Families

λ> :kind! Eval ((Snd <=< FromMaybe '(0, 0))
                     =<< Pure (Just '(1,2)))
Eval ((Snd <=< FromMaybe '(0, 0))
           =<< Pure (Just '(1,2))) :: Nat
= 2

Package called first-class-families
Provides:
- (Single) Open type family Eval
- Kind constructor Exp
  - Forms a type-level monad
- Variety of Prelude functions as defunctionalized data declarations with Eval type instances

{-# LANGUAGE DataKinds, PolyKinds, TypeFamilies,
    TypeInType, TypeOperators, UndecidableInstances #-}

What's Next?

Type Variables in Patterns
- Visible Type on the LHS
Binding Type Variables in Lambdas
FCF Expansion
Dependent Haskell

Title Text

Resources

Introductory
- Basic Type Level Programming (Blog)
- Thinking With Types (Book)
Type Variables
- Type Variables in Patterns (Paper)
Servant
- Servant, Type Families, and Type-level Everything (Blog)
- Why is servant a type-level DSL? (Blog)
- Type-level Web APIs with Servant (Paper)
First Class Families
- Haskell with one Type Family (blog)
Future
- GHC Proposals

Type Level Programming

Plan

What am I skipping?

Typical Haskell

Type-Level Haskell

Kinds

Type Level Programming

Beware!

Haskell Primer

Data Types

Functions

Data Types

Data Types

Functions

Functions

Functions

Functions

Functions

Classes and Instances

Classes and Instances

Algebra of Types

Algebra behind ADTs

Algebra behind ADTs

Isomorphism

Isomorphism

Isomorphism

Identity

Cardinality of (->)

Cardinality of (->)

Curry-Howard Isomorphism

Insights from Curry-Howard Isomorphism

Canonical Representations

Kind System

Kinds

Constraint Kinds

PolyKinds

DataKinds

GADTs

Type Equality

GADTS

GADTS

GADTS

GADTS

Type Families

Closed Type Families

Open Type Families

Saturation

Associated Type Families

Associated Type Families

Type Variables

Visible Type Applications

Scoped Type Variables

Need for Type Annotations

Type-class ambiguity

Polymorphic Recursion

GADTS

Ambiguous Types

Rank Polymorphism

Rank Polymorphism

Example

Rank Polymorphism

Rank Polymorphism

Rank Polymorphism

Counting Rank

Counting Rank

First Class Families

Defunctionalization

Defunctionalizing Higher Order Functions

Type-Level Defunctionalization

More

More

Higher Order Type Functions

First Class Families

What's Next?

What's Next?

Title Text

Resources