Cosmological inference at the field-level

Hugo SIMON-ONFROY,
PhD student supervised by
Arnaud DE MATTIA and François LANUSSE
DPhP, 2025/01/16
Current estimation
A toy example

\(\Omega := \{ \Omega_c, \Omega_b, \Omega_\Lambda, H_0, \sigma_8, n_s,...\}\)
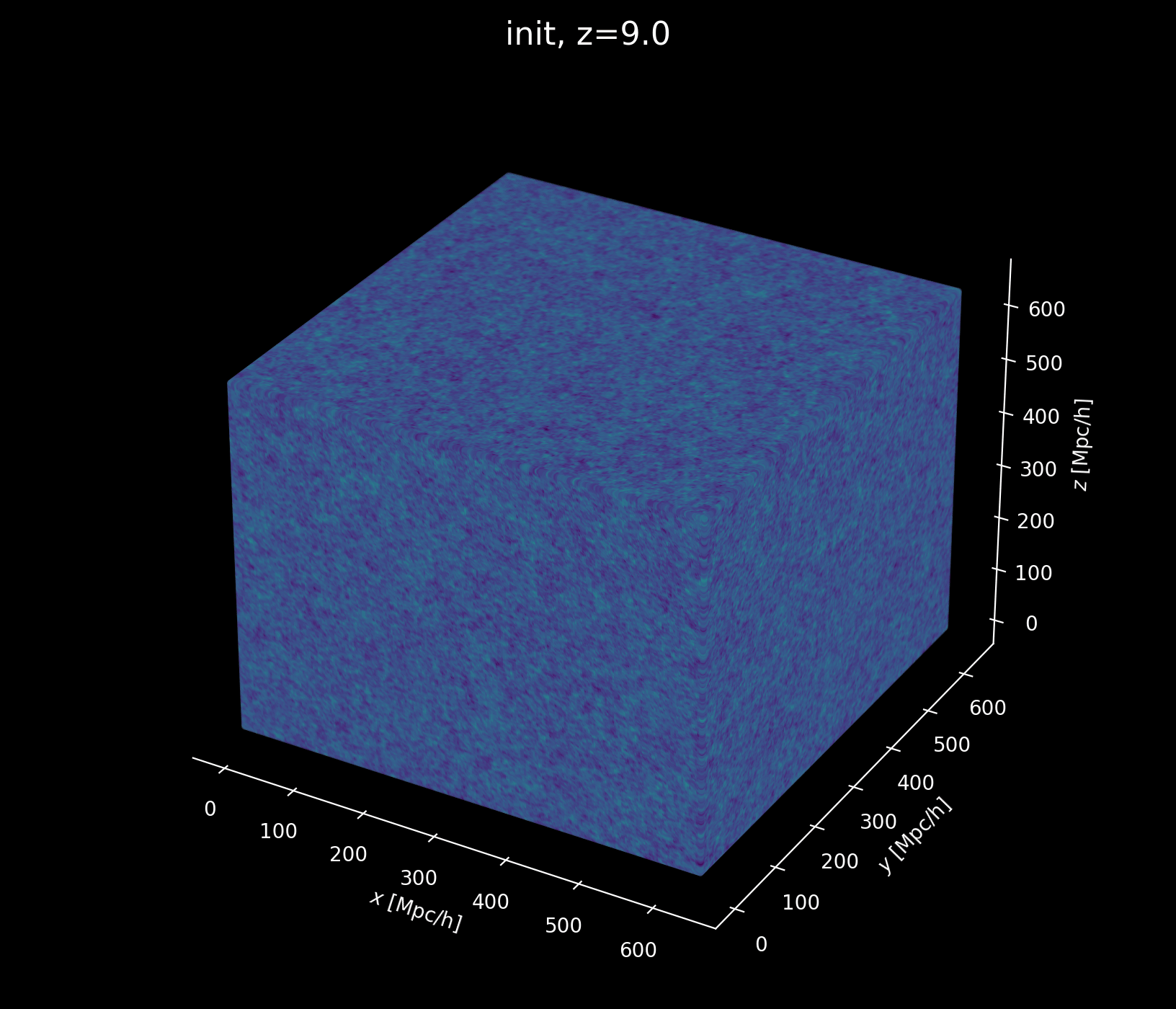
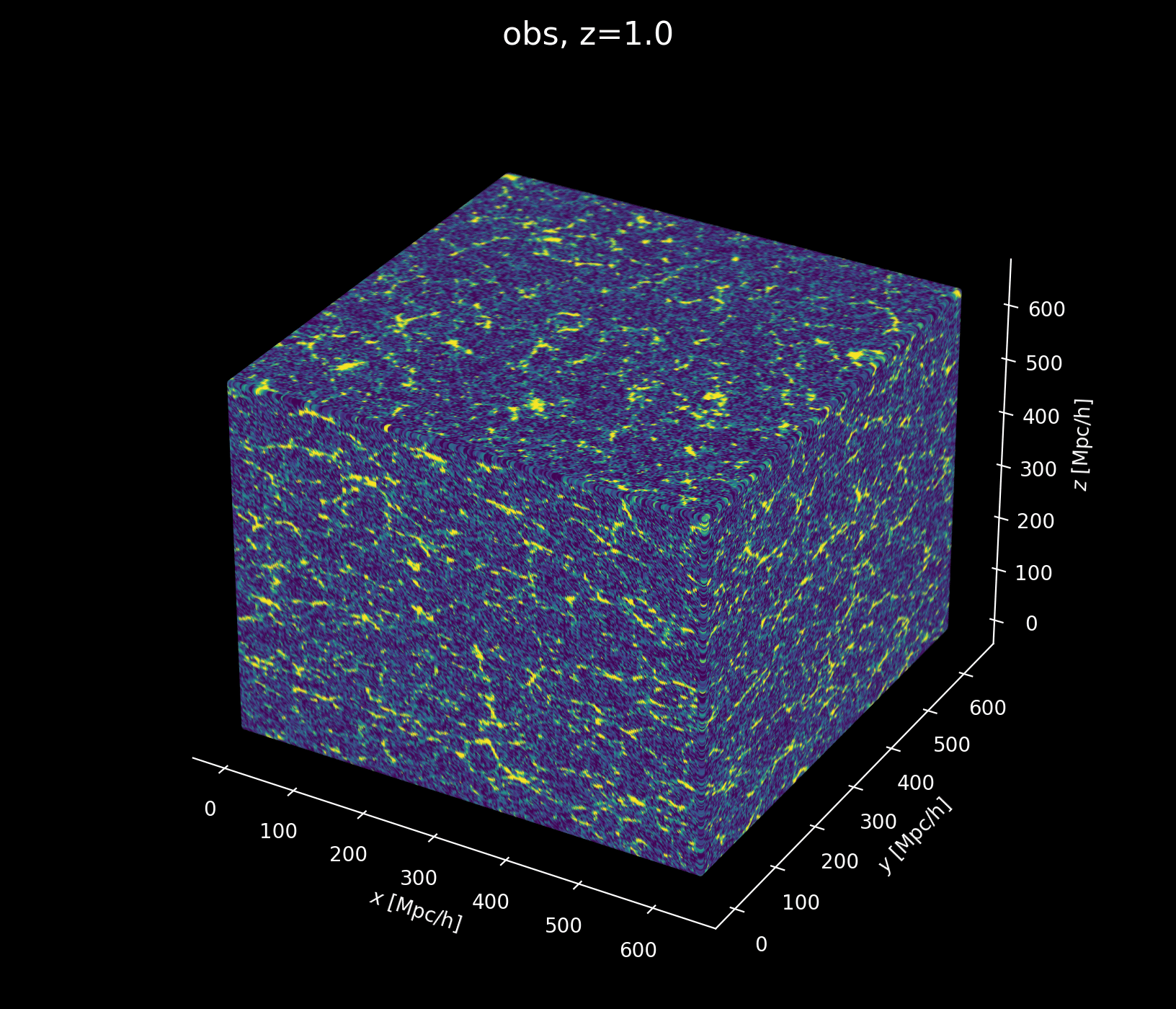
Linear matter spectrum
Structure growth
Cosmological modeling and inference
\(\Omega\)
\(\delta_L\)
\(\delta_g\)
inference
$$\boldsymbol{p}(\Omega \mid \delta_g) \propto \int \boldsymbol{p}(\Omega, \delta_L, \delta_g) \;\mathrm d \delta_L$$

\(\Omega := \{ \Omega_c, \Omega_b, \Omega_\Lambda, H_0, \sigma_8, n_s,...\}\)


Linear matter spectrum
Structure growth
Can't integrate? Then compress
\(\Omega\)
\(\delta_L\)
\(\delta_g\)
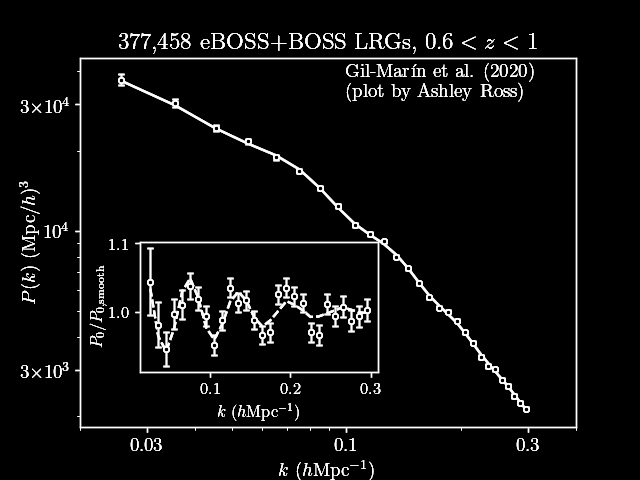
\(P\)
Power spectrum \(P(\delta_g)\) allows to analytically compute $$\boldsymbol{p}(\Omega \mid P) \propto \int \boldsymbol{p}(\Omega, \delta_L, P) \;\mathrm d \delta_L$$
Compression
If \(\delta_g\) is Gaussian, \(P\) is a lossless compression and then $$\boldsymbol{p}(\Omega \mid P) = \boldsymbol{p}(\Omega \mid \delta_g)$$
But...
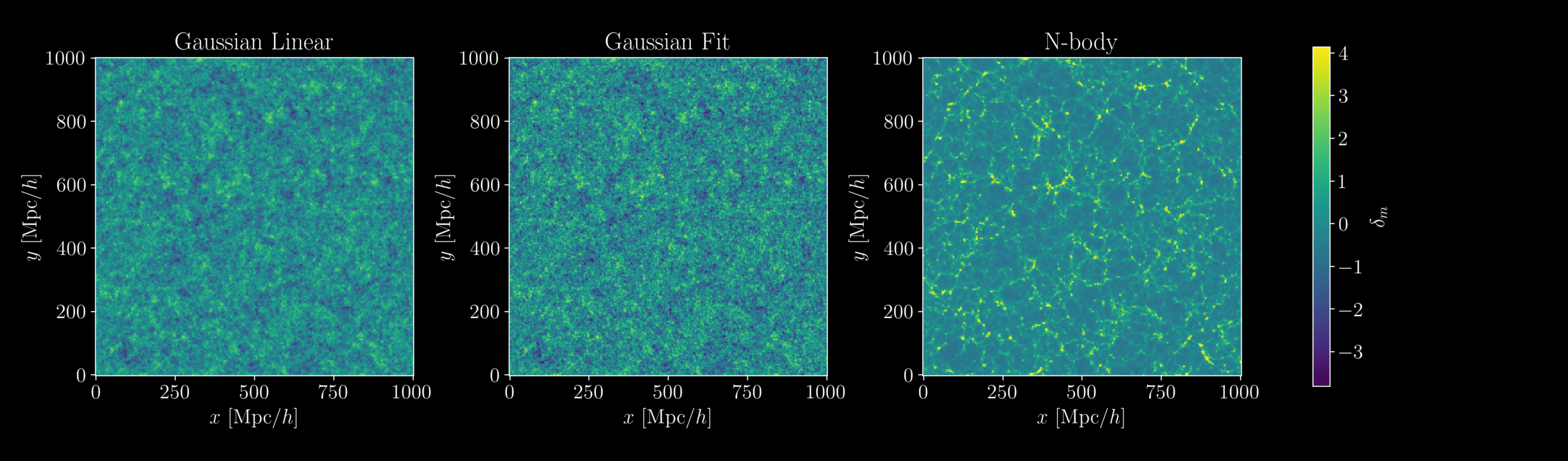
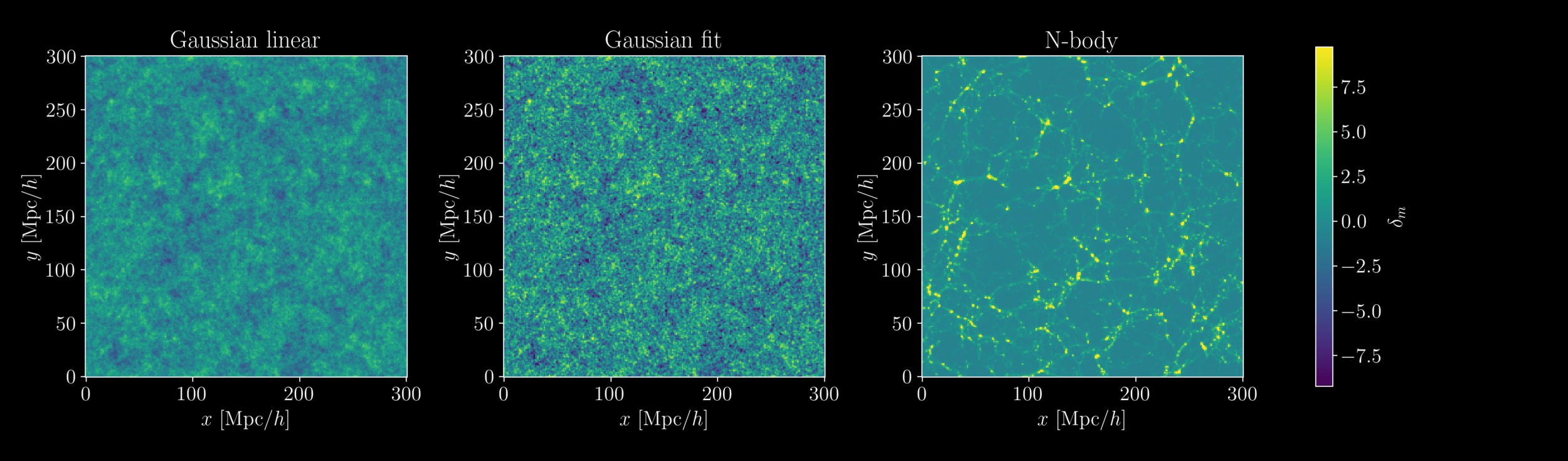
- At large scales, matter field almost Gaussian so power spectrum is almost lossless compression
- At smaller scales however, matter field is non-Gaussian
Gaussianity and beyond
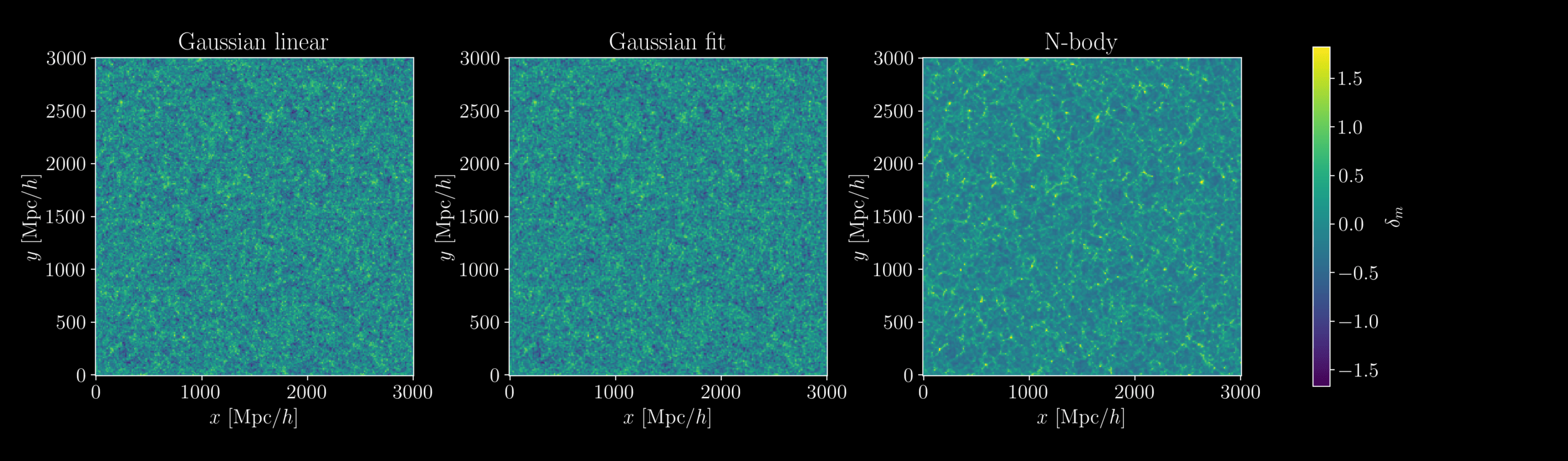
2 fields, 1 power spectrum: Gaussian or N-body?
Field-level inference
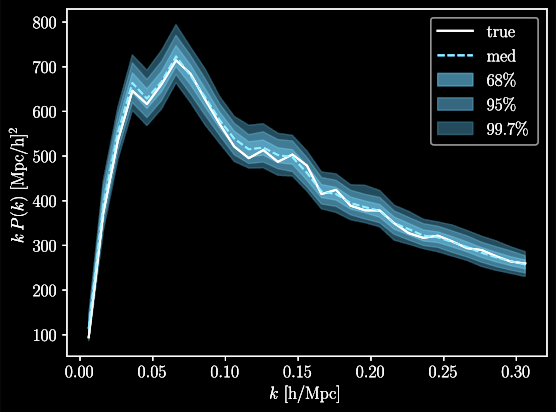
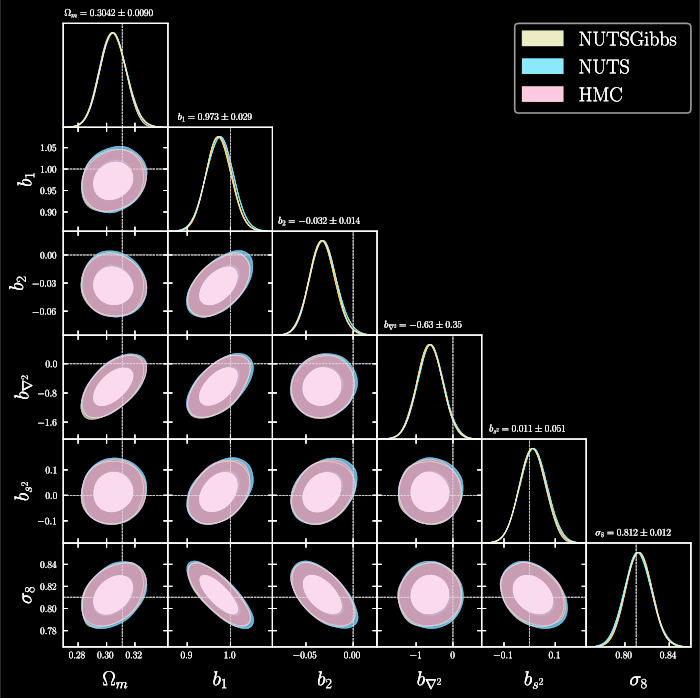
Idea: sample simultaneously cosmology and initial field, yielding posterior on full universe history

- High dimensional sampling: \(1024^3\) params!
- Use gradient-based MCMC such as Hamiltonian Monte Carlo, thanks to auto-diff