SCALABLE BAYESIAN INFERENCE WITH DIFFERENTIABLE SIMULATORS FOR THE
COSMOLOGICAL ANALYSIS OF THE DESI SPECTROSCOPIC SURVEY

Hugo SIMON-ONFROY,
PhD student supervised by Arnaud DE MATTIA and François LANUSSE
CSI, 2024/10/18
Benchmarking field-level inference from galaxy surveys

Hugo SIMON-ONFROY,
PhD student supervised by Arnaud DE MATTIA and François LANUSSE
DESI Marseille meeting, 2024/07/12
Field-level inference from galaxy surveys

Hugo SIMON-ONFROY,
PhD student supervised by Arnaud DE MATTIA and François LANUSSE
Rodolphe Clédassou Summer School, 2024/08
The universe recipe (so far)
$$\frac{H}{H_0} = \sqrt{\Omega_r + \Omega_b + \Omega_c+ \Omega_\kappa + \Omega_\Lambda}$$
instantaneous expansion rate
energy content
Cosmological principle + Einstein equation
+ Inflation
\(\delta_L \sim \mathcal G(0, \mathcal P)\)
\(\sigma_8:= \sigma[\delta_L * \boldsymbol 1_{r \leq 8}]\)
initial field
primordial power spectrum
std. of fluctuations smoothed at \(8 \text{ Mpc/h}\)


\(\Omega := \{ \Omega_c, \Omega_b, \Omega_\Lambda, H_0, \sigma_8, n_s,...\}\)

Linear matter spectrum
Structure growth

$$\begin{align*}\operatorname{\boldsymbol{H}}(\Omega\mid \delta_g) &= \boldsymbol{H}(\delta_g \mid \Omega) + \boldsymbol{H}(\Omega) - \boldsymbol{H}(\delta_g)\\&= \boldsymbol{H}(\Omega) - \boldsymbol{I}(\Omega;\delta_g) \leq \boldsymbol{H}(\Omega)\end{align*}$$
$$\boldsymbol{I}(\Omega; \delta_g)$$
\(\boldsymbol{H}(X)\) = missing info on \(X\)
$$\boldsymbol{H}(\Omega)$$
$$\boldsymbol{H}(\delta_g)$$
$$\boldsymbol{H}(\Omega\mid\delta_g)$$
A high-dimensional inference problem



\(\Omega := \{ \Omega_c, \Omega_b, \Omega_\Lambda, H_0, \sigma_8, n_s,...\}\)



Linear matter spectrum
Structure growth

- Cosmological model links cosmo \(\Omega\) to initial field \(\delta_L\) to galaxy density field \(\delta_g\)
- Cosmological parameter inference obtained via marginalizing full posterior over initial field$$\boldsymbol{p}(\Omega \mid \delta_g) = \int \boldsymbol{p}(\Omega, \delta_L \mid \delta_g) \;\mathrm d \delta_L$$
A high-dimensional inference problem
How to perform this marginalization?


\(\Omega := \{ \Omega_c, \Omega_b, \Omega_\Lambda, H_0, \sigma_8, n_s,...\}\)



Linear matter spectrum
Structure growth

- Cosmological model links cosmo \(\Omega\) to initial field \(\delta_L\) to galaxy density field \(\delta_g\)
- Cosmological parameter inference obtained via marginalizing full posterior over initial field$$\boldsymbol{p}(\Omega \mid \delta_g) = \int \boldsymbol{p}(\Omega, \delta_L \mid \delta_g) \;\mathrm d \delta_L$$
A high-dimensional inference problem
How to perform this marginalization?
Bayes, information flavor

$$\boldsymbol{H}(X\mid Y_1)$$
$$\boldsymbol{H}(X)$$
$$\boldsymbol{H}( Y_1)$$
$$\boldsymbol{I}(X; Y_1)$$
$$\boldsymbol{H}( Y_2)$$
$$\boldsymbol{I}(X\mid Y_1; Y_2)$$
$$\boldsymbol{H}(X\mid Y_1,Y_2)$$
\(\boldsymbol{H}(X)\) = missing information on \(X\) = amount of bits to communicate \(X\)
$$\boldsymbol{H}(X\mid Y_1)$$
$$\begin{align*}\operatorname{\boldsymbol{H}}(X\mid Y) &= \boldsymbol{H}(Y \mid X) + \boldsymbol{H}(X) - \boldsymbol{H}(Y)\\&= \boldsymbol{H}(X) - \boldsymbol{I}(X;Y) \leq \boldsymbol{H}(X)\end{align*}$$
Use summary statistics
Marginalize then sample
- build a marginal model linking cosmo \(\Omega\) and some summary stat \(s\), then sample from simpler \(\boldsymbol p(\Omega \mid s)\)
- trade-off analytical/variational tractability vs. info content of \(s\)





summary stat inference
A tractable candidate: the power spectrum

We gotta pump this information up
- Field-level
- CNN...
- WST...
- Halo, Peak, Void, Split, Hole...
- 3PCF, Bispectrum
- 2PCF, Power spectrum
- 1D-PDF

$$0-$$
$$\boldsymbol H(\delta_g)-$$













- At large scales, matter density field almost Gaussian so power spectrum is almost lossless compression.
- To prospect smaller non-Gaussian scales, let's use:
We gotta pump this information up
- Field-level
- CNN, GNN...
- WST, 1D-PDFs, Holes...
- Peak, Void, Split, Cluster...
- 3PCF, Bispectrum
- 2PCF, Power spectrum

$$0-$$
$$\boldsymbol H(\delta_g)-$$













- At large scales, matter density field almost Gaussian so power spectrum is almost lossless compression, and is relatively tractable
- To prospect smaller non-Gaussian scales, let's add:
- all the data
- learn the stat
- multiscale count
- object correlations
- more correlations
- standard analysis

-
Marginalize then sample
- build a marginal model linking cosmo \(\Omega\) and some summary stat \(s\)
- trade-off analytical/variational tractability vs. info content of \(s\)
-
Sample then marginalize
- full history reconstruction without info loss
- requires simulating LSS formation for each sample
Compress or not compress
How much information can we still gain (not lose)?






Model based field-level inference
summary stat inference
More information is better,
but how much better?
Model Based Inference at the field level
(explicitly solve)

How much information can we still gain (not lose)?






field-level inference
summary stat inference
For full field marginalize then sample hardly tractable,
so sample then marginalize
- sample jointly \(\Omega\) and \(\delta_L\), then marginalize over \(\delta_L\) samples
- full history reconstruction without info loss
- requires simulating LSS formation for each sample
- for probing non-Gaussian scales of interest in DESI volume \(\operatorname{dim}(\delta_L)\geq1024^3\)
A high-dimensional sampling problem


Some useful programming tools
-
NumPyro
- Probabilistic Programming Language (PPL)
- Powered by JAX
- Integrated samplers
-
JAX
-
GPU acceleration
- Just-In-Time (JIT) compilation acceleration
- Automatic vectorization/parallelization
- Automatic differentiation
-
GPU acceleration

- Prior on
- Cosmology \(\Omega\)
- Initial field \(\delta_L\)
- Dark matter-galaxy connection (Lagrangian galaxy biases) \(b\)
- Initialize matter particles
- LSS formation (LPT+PM)
- Populate matter field with galaxies
- Galaxy peculiar velocities (RSD)
- Observational noise
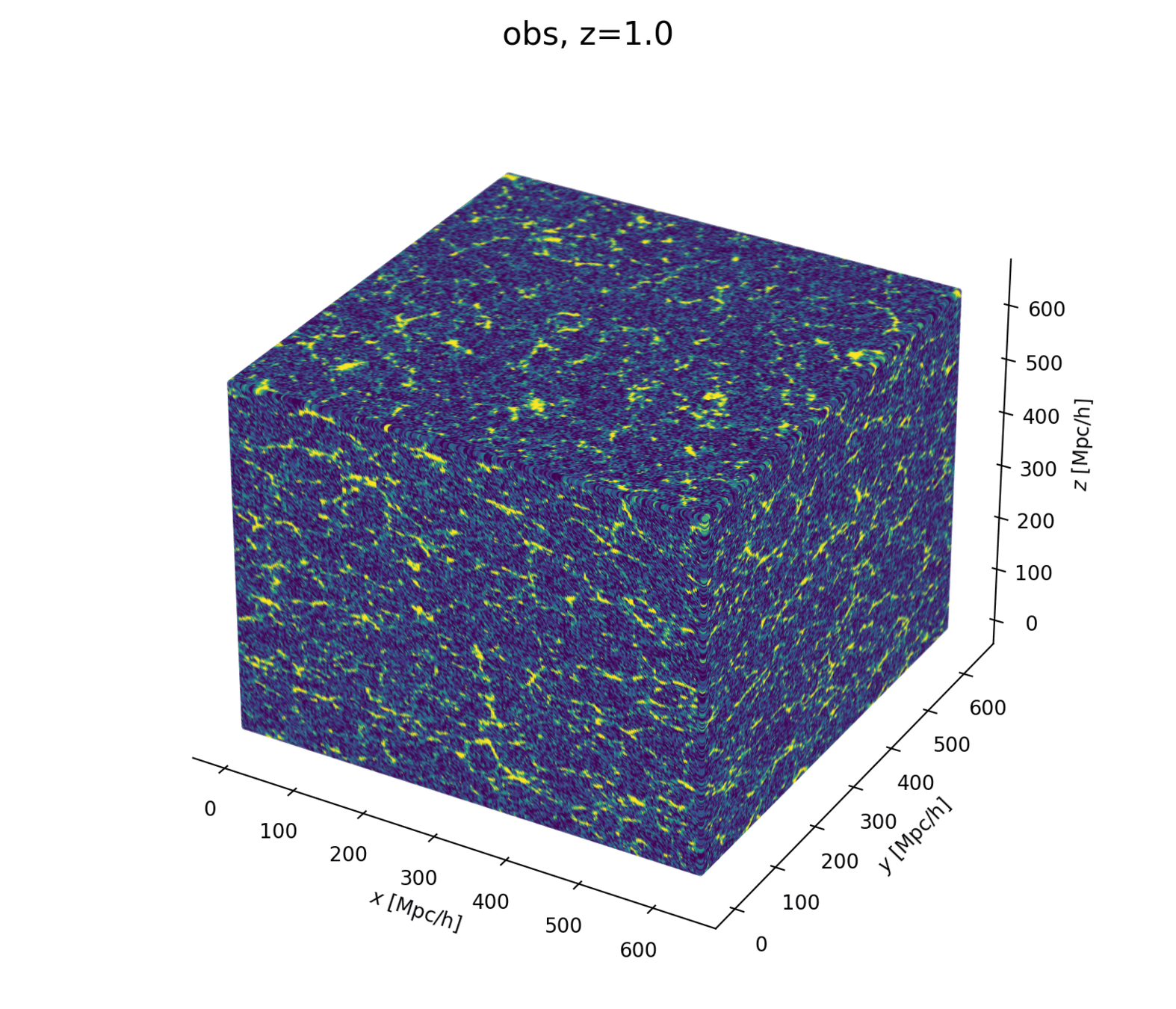
Let's build a cosmological model
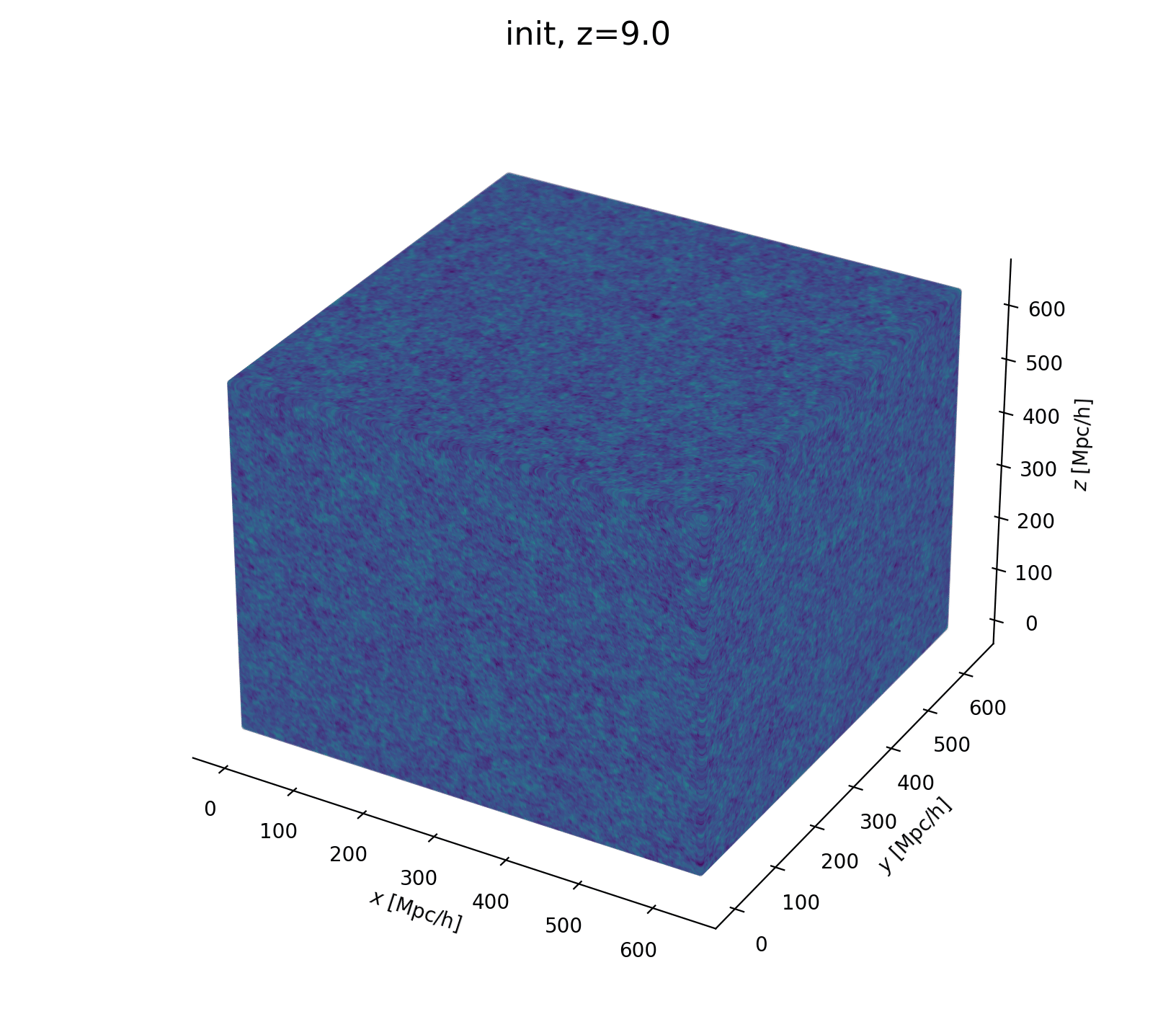
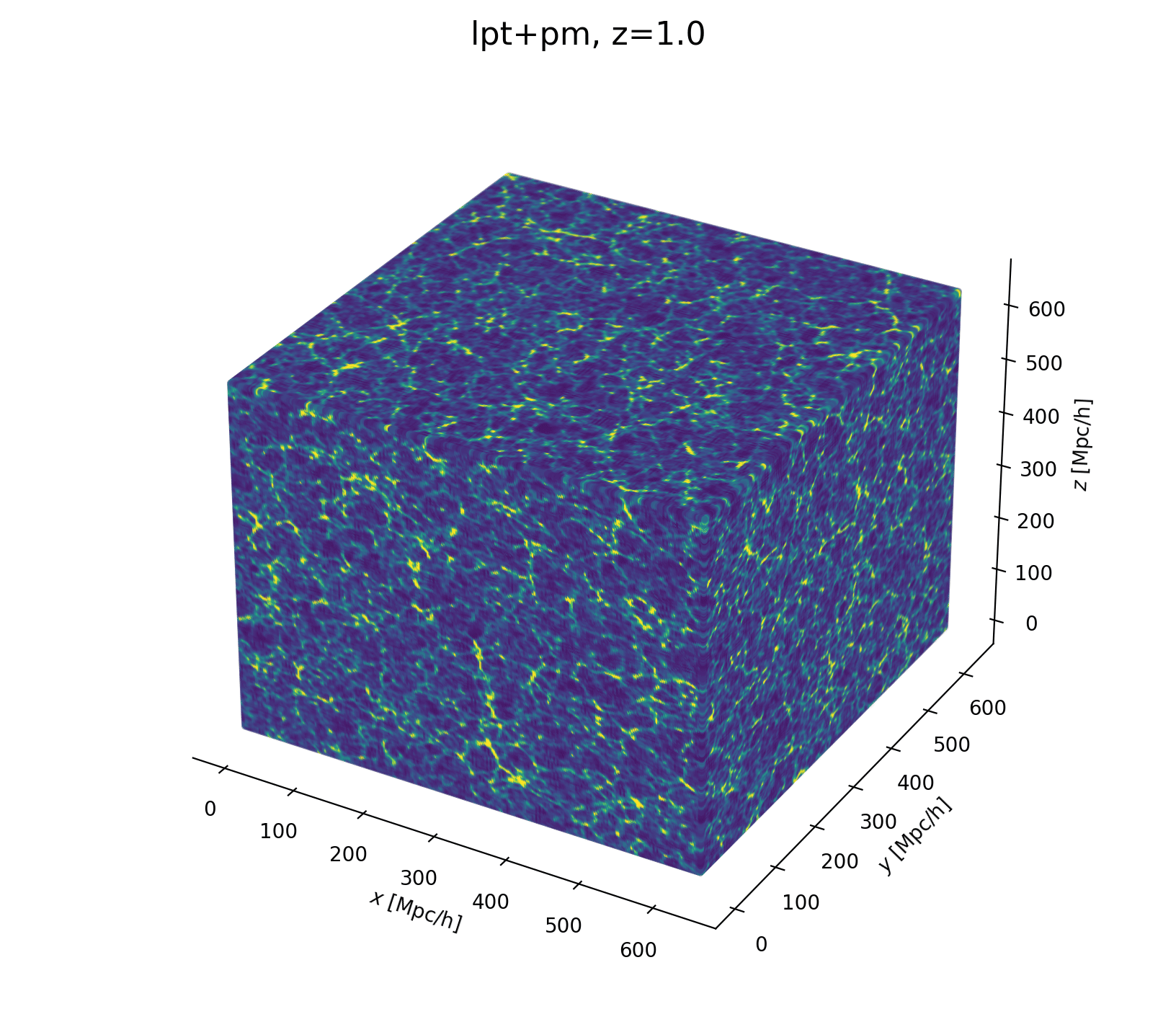
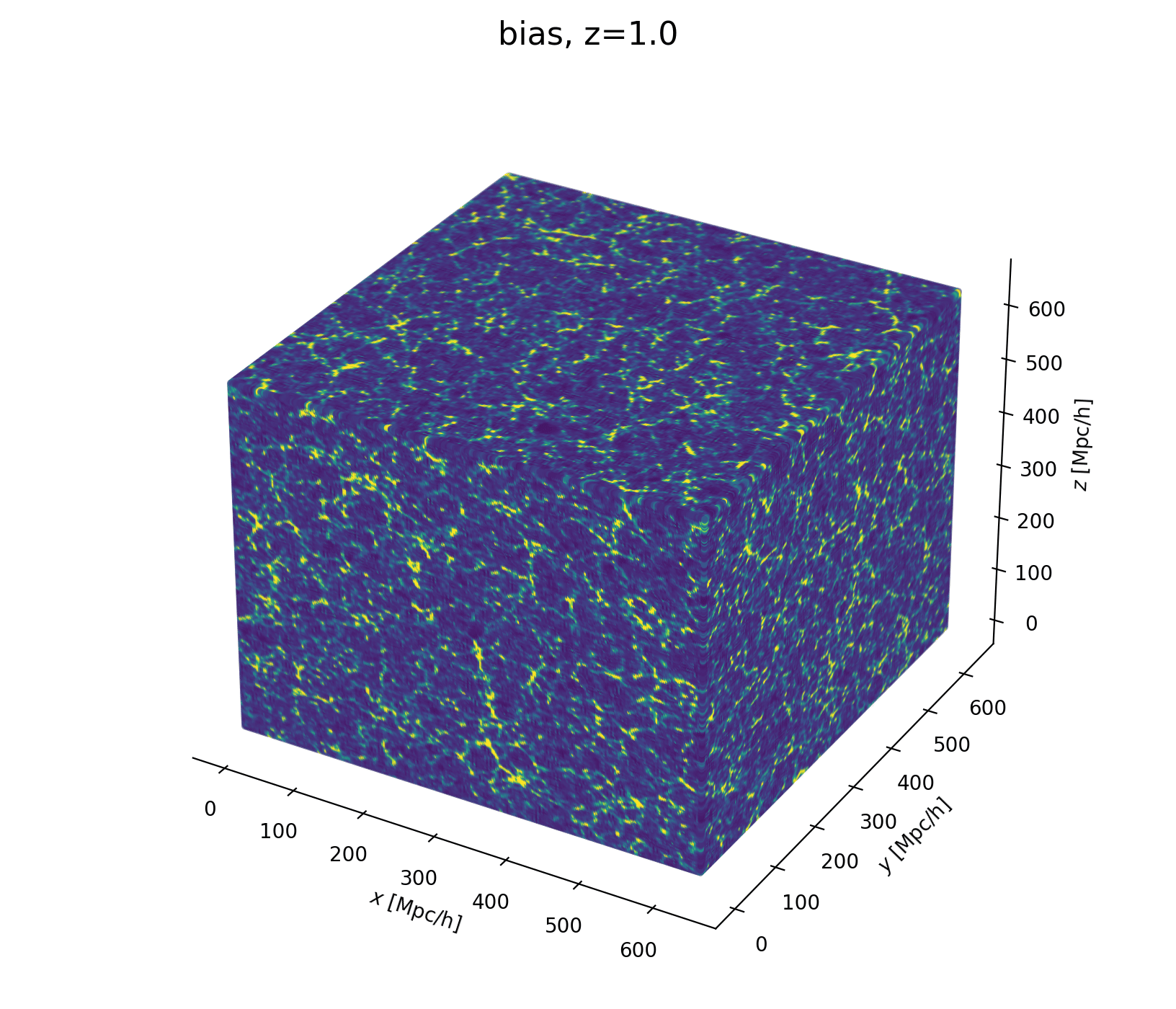
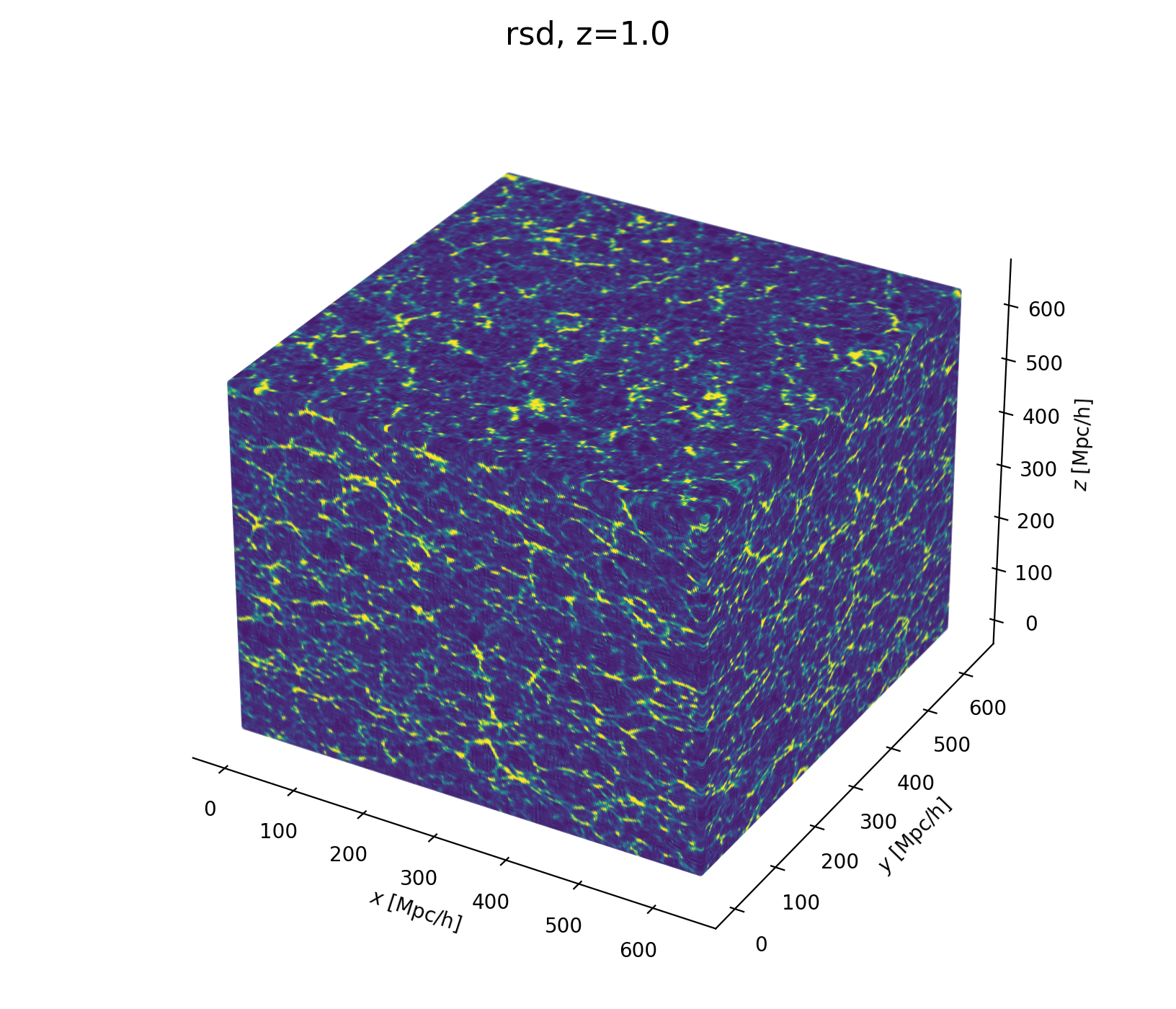
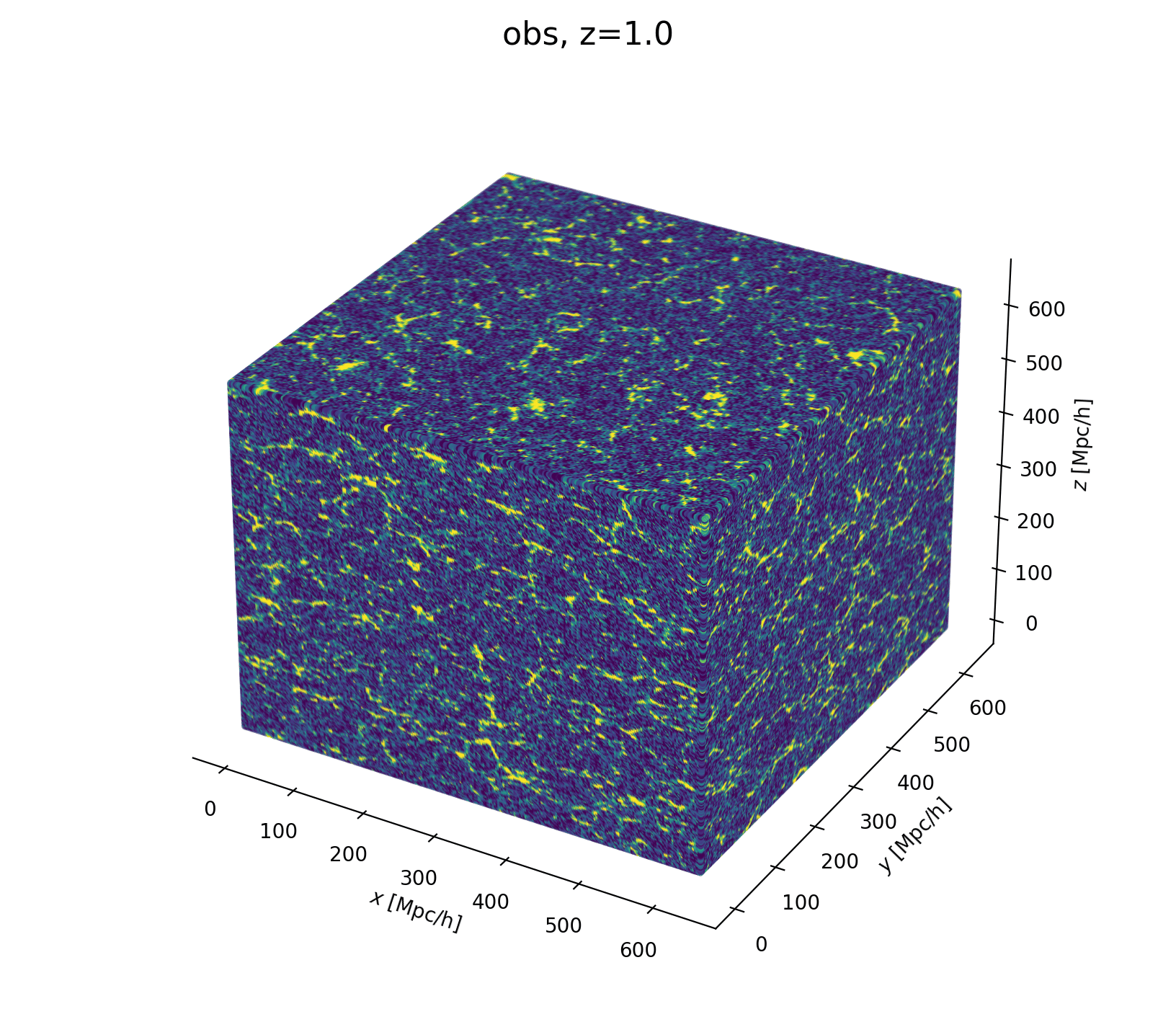
- Fast and differentiable model thx to JaxPM
- still, \(\simeq 1024^3\) parameters is huge!
- Some proposed methods by Lavaux+2018, Bayer+2023
Which sampling methods can scale to high dimensions?

- Prior on
- Cosmology \(\Omega\)
- Initial field \(\delta_L\)
- Dark matter-galaxy connection (Lagrangian galaxy biases) \(b\)
- Cosmology \(\Omega\)
- Initialize matter particles
- LSS formation (LPT+PM)
- Populate matter field with galaxies
- Galaxy peculiar velocities (RSD)
- Observational noise
Now let's build a cosmological model





- \(\simeq 1024^3\) parameters is huge!
- Need inference methods that scale to high dimensions
- Some proposed by Lavaux+2018, Bayer+2023
- Fast and differentiable model
- No need to approx likelihood for your favorite stat from simulation:
the simulation is the likelihood
Why care about differentiable model?
-
Classical MCMCs
-
agnostic random moves
+ MH acceptance step
= blinded natural selection
- small moves yield correlated samples.
-
agnostic random moves
- SOTA MCMCs rely on the gradient of the model log-proba, to drive dynamic towards highest density regions.

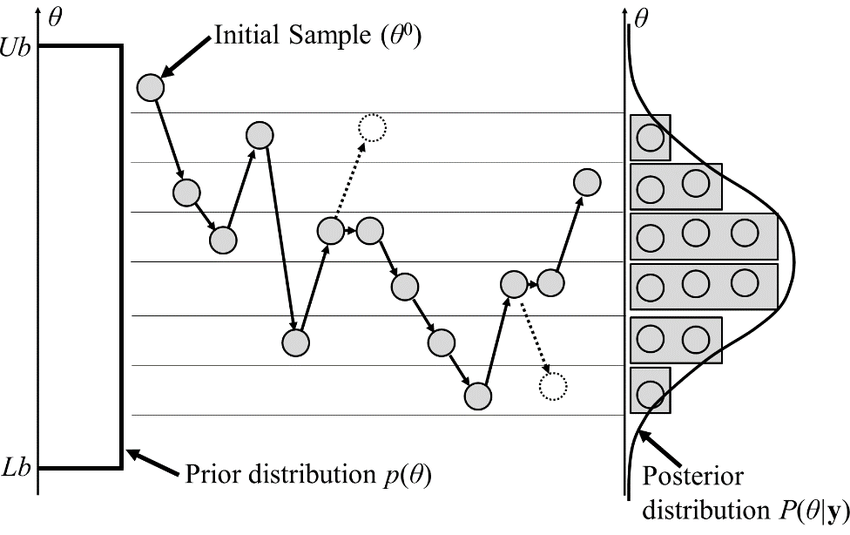
gradient descent
posterior mode
Brownian
exploding Gaussian
Langevin
posterior
+
=


Hamiltonian Monte Carlo (HMC)
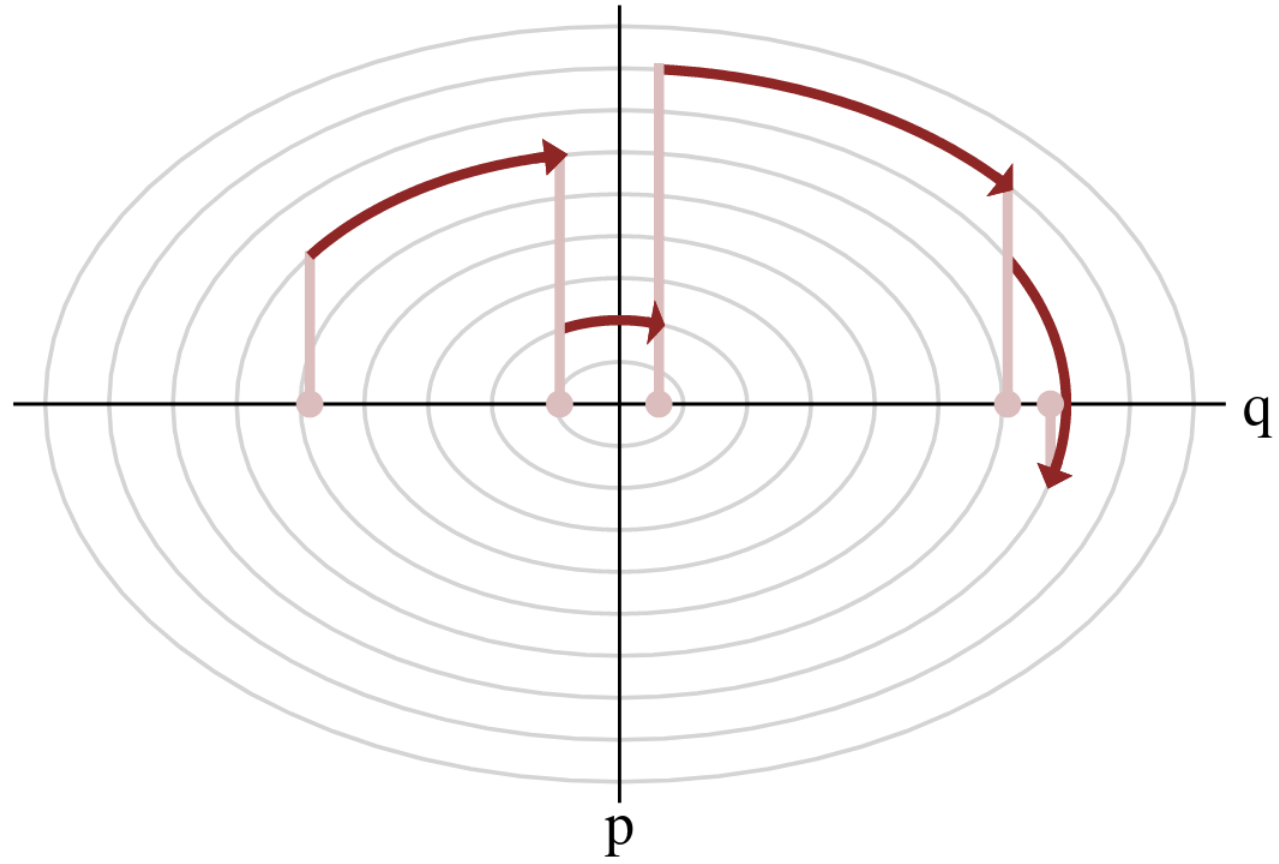
- To travel farther, add inertia.
- sample particle at position \(q\) now have momentum \(p\) and mass matrix \(M\)
- target \(\boldsymbol{p}(q)\) becomes \(\boldsymbol{p}(q , p) := e^{-\mathcal H(q,p)}\), with Hamiltonian $$\mathcal H(q,p) := -\log \boldsymbol{p}(q) + \frac 1 2 p^\top M^{-1} p$$
- at each step, resample momentum \(p \sim \mathcal N(0,M)\)
- let \((q,p)\) follow the Hamiltonian dynamic during time length \(L\), then arrival becomes new MH proposal.

Variations around HMC
-
No U-Turn Sampler (NUTS)
- trajectory length \(L\) auto-tuned
- samples drawn along trajectory
- NUTSGibbs i.e. alternating sampling over parameter subsets.
Why care about differentiable model?

Variations around HMC
-
No U-Turn Sampler (NUTS)
- trajectory length auto-tuned
- samples drawn along trajectory
- NUTSGibbs i.e. alternating sampling over parameter subsets
-
Model gradient drives sample particles towards high density regions
-
Hamiltonian Monte Carlo (HMC):
to travel farther, add inertia
- Yields less correlated chains

3) Hamiltonian dynamic
1) mass \(M\) particle at \(q\)
2) random kick \(p\)
2)random kick \(p\)
1) mass \(M\) particle at \(q\)
3) Hamiltonian dynamic

Benchmarking
- model setting: \(64^3\) mesh, \((640\textrm{ Mpc/h})^3\) box, 1LPT, 2nd order Lagrangian bias expansion, RSD and Gaussian observational noise.
- parameter space: initial field \(\delta_L\), cosmology \(\Omega\! =\! \{\Omega_m, \sigma_8\}\), and galaxy biases \(b\!=\!\{b_1,b_2,b_{s^2},b_{\nabla^2}\}\). Total of \(64^3 + 2 +4\) parameters.
- For NUTSGibbs: split sampling between \(\delta_L\) and the rest (common in lit.)
- Results suggest no particular advantage to splitting sampling between initial field and rest, cf. Simon-Onfroy et al. in prep


Reconstruct the initial field simultaneously, yielding posterior on full universe history
number of evaluations to yield one effective sample: the higher the worse



Activities 2023-2024
- Schools
- Rodolphe Clédassou (2023, 2024)
- Bayes@CIRM (2023)
- Teaching
- M1 Maths and L2 Biostats at UPS
- Conferences and workshops
- ML in Astro IAP/CCA
- Poster at Cosmo21
- Talk at EDSU Tools
- Talk a DESI meeting
- Bayes intro at Cosmostat
- Visit at Flatiron Institute
- DESI observing (cloudy...)
...and what's next
-
1st author paper (< December 2024)
- benchmark more proposed samplers
- compare to SBI approaches
- Longer term
- applications on DESI data (survey selection fct)
- annealing/diffusion based sampler
Recap...
-
Leverage modern computational tools to build fast and differentiable cosmological model
-
Field-level inference can scale to Stage-IV galaxy surveys, and is relevant to fully capture cosmological information from data
...and what's next
- Include more proposed samplers.
- Compare to SBI approaches.
- Move towards applications on DESI data.
Recap...
-
Field-level inference may be relevant to fully capture cosmological information in data.
-
Leverage modern computational tools to build fast and differentiable cosmological model.
-
Standardized benchmark for comparing MCMC samplers on field-level inference tasks, selecting proposed methods for Stage-IV galaxy surveys.
- At large scales, matter density field almost Gaussian so power spectrum is almost lossless compression
- At smaller scales however, matter density field non-Gaussian
Gaussianity and beyond
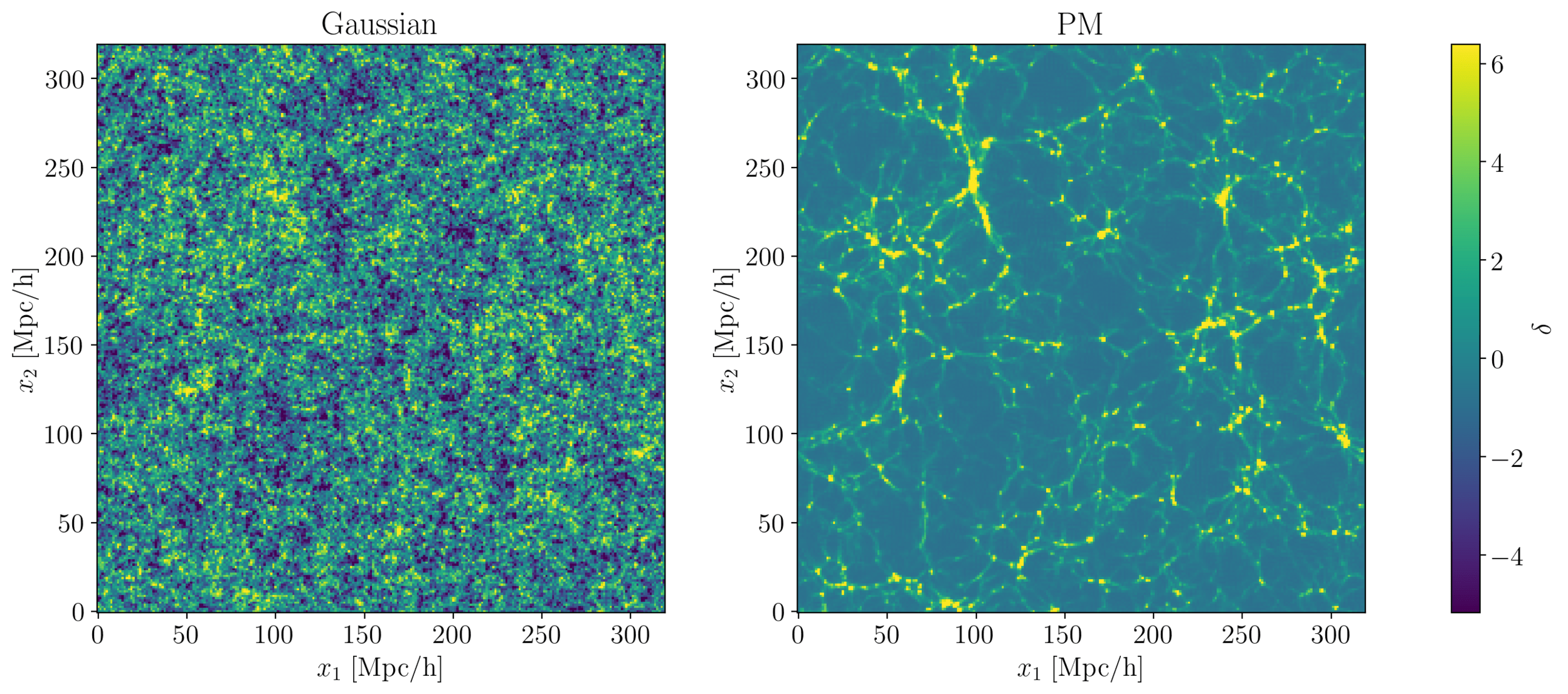
2 fields, 1 power spectrum: Gaussian or N-body?
$$\boxed{\min_s \operatorname{\boldsymbol{H}}(\Omega\mid s(\delta_g))} = \boldsymbol{H}(\Omega) - \max_s \boldsymbol{I}(\Omega ; s(\delta_g))$$
$$\boldsymbol{H}(\Omega)$$
$$\boldsymbol{H}(\delta_g)$$
$$\boldsymbol{H}(\mathcal s_1)$$
$$\boldsymbol{H}(\mathcal s_2)$$
$$\boldsymbol{H}(\mathcal P)$$
non-Gaussianities
relevant stat
(low info but high mutual info)
irrelevant stat
(high info but low mutual info)
also a relevant stat
(high info and mutual info)
Which stats are relevant for cosmo inference?
Gaussianities
Compress or not compress
So JAX in practice?
-
GPU accelerate
- JIT compile
- Vectorize/Parallelize
- Auto-diff
import jax.numpy as np
# then enjoyfunction = jax.jit(function)
# function is so fast now!gradient = jax.grad(function)
# too bad if you love chain ruling by handvfunction = jax.vmap(function)
pfunction = jax.pmap(function)
# for-loops are for-loosers


So NumPyro in practice?
def model():
z = sample('Z', dist.Normal(0, 1))
x = sample('X', dist.Normal(z**2, 1))
return x
render_model(model, render_distributions=True)
x_sample = dict(x=seed(model, 42)())
obs_model = condition(model, x_sample)
logp_fn = lambda z: log_density(obs_model,(),{},{'Z':z})[0]from jax import jit, vmap, grad
score_vfn = jit(vmap(grad(logp_fn)))kernel = infer.NUTS(obs_model)
mcmc = infer.MCMC(kernel, num_warmup, num_samples)
mcmc.run(PRGNKey(43))
samples = mcmc.get_samples()- Probabilistic Programming
- JAX machinery
- Integrated samplers

-
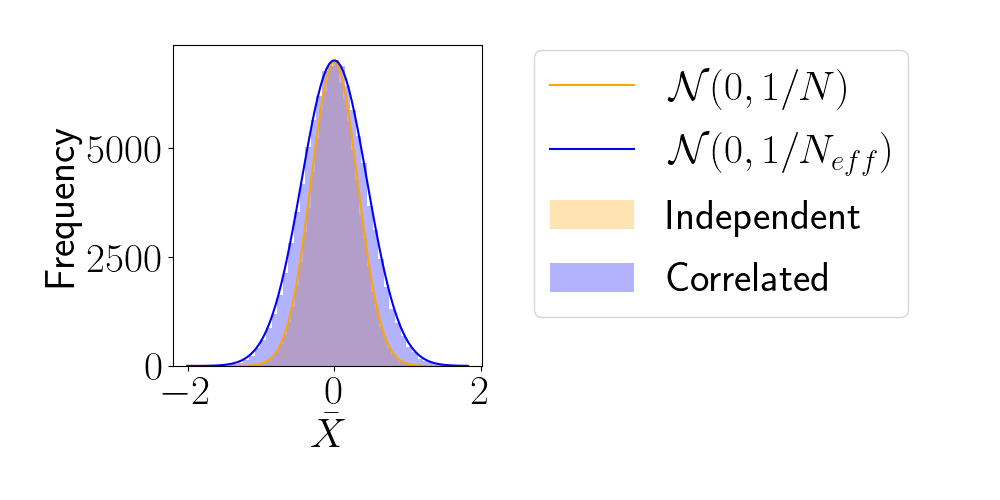
Effective Sample Size (ESS)
- number of i.i.d. samples that yield same statistical power.
- For sample sequence of size \(N\) and autocorrelation \(\rho\) $$N_\textrm{eff} = \frac{N}{1+2 \sum_{t=1}^{+\infty}\rho_t}$$so aim for as less correlated sample as possible.
- Main limiting computational factor is model evaluation (e.g. N-body), so characterize MCMC efficiency by \(N_\text{eval} / N_\text{eff}\)