Implicit full-field inference for LSST weak Lensing

Justine Zeghal

Supervisors: François Lanusse, Alexandre Boucaud, Eric Aubourg

Tri-state Cosmology x machine learning journal club

 January 19, Paris, France

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

How to extract all the information embedded in our data?

Standard analysis relies on 2-point statistics and use a Gaussian analytic likelihood.

But these summary statistics is suboptimal at small scales..

Full-field inference 2 ways..

  • Bayesian hierarchical modeling

Full-field inference 2 ways..

\theta
z
f
\sigma^2
\mathcal{N}
x

Full-field inference 2 ways..

  • Bayesian hierarchical modeling
\theta
z
f
\sigma^2
\mathcal{N}

Explicit joint likelihood

 

p(x| \theta, z)

Full-field inference 2 ways..

  • Bayesian hierarchical modeling
x
z

And then run an MCMC to get the posterior:

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

And then run an MCMC to get the posterior:

  • Bayesian hierarchical modeling
\theta
f
\sigma^2
\mathcal{N}

Explicit joint likelihood

 

p(x| \theta, z)

Full-field inference 2 ways..

x

It provides exact results but necessitates the BHM to be differentiable and requires a lot of simulations.

And then run an MCMC to get the posterior:

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

And then run an MCMC to get the posterior:

  • Bayesian hierarchical modeling
z
\theta
f
\sigma^2
\mathcal{N}

Explicit joint likelihood

 

p(x| \theta, z)

Full-field inference 2 ways..

x
  • Implicit inference with sufficient statistics

Full-field inference 2 ways..

  • Implicit inference with sufficient statistics
z
\theta
f
\sigma^2
\mathcal{N}

Full-field inference 2 ways..

x
\theta
z
f
\sigma^2
\mathcal{N}
  • Implicit inference with sufficient statistics

Full-field inference 2 ways..

 Simulator

x
\theta

Summary statistics

t = f_{\varphi}(x)
z
f
\sigma^2
\mathcal{N}
  • Implicit inference with sufficient statistics

Full-field inference 2 ways..

 Simulator

x
\theta
z
f
\sigma^2
\mathcal{N}
(\theta_i, t_i)_{i=1...N}
  • Implicit inference with sufficient statistics

Full-field inference 2 ways..

 Simulator

(\theta|
p_{\Phi}
f_{\varphi}(x)
)

And use neural-based likelihood-free approaches to get the posterior

 

 

using only:

Summary statistics

t = f_{\varphi}(x)
x
\theta
z
f
\sigma^2
\mathcal{N}

And use neural-based likelihood-free approaches to get the posterior

 

 

using only:

(\theta_i, t_i)_{i=1...N}
  • Implicit inference with sufficient statistics

Full-field inference 2 ways..

 Simulator

(\theta|
p_{\Phi}
f_{\varphi}(x)
)

Summary statistics

t = f_{\varphi}(x)
x
\theta
z
f
\sigma^2
\mathcal{N}

And use neural-based likelihood-free approaches to get the posterior

 

 

using only:

(\theta_i, t_i)_{i=1...N}
  • Implicit inference with sufficient statistics

Full-field inference 2 ways..

 Simulator

(\theta|
p_{\Phi}
f_{\varphi}(x)
)

Summary statistics

t = f_{\varphi}(x)
x
\theta
z
f
\sigma^2
\mathcal{N}

And use neural-based likelihood-free approaches to get the posterior

 

 

using only:

(\theta_i, t_i)_{i=1...N}
  • Implicit inference with sufficient statistics

Full-field inference 2 ways..

 Simulator

(\theta|
p_{\Phi}
f_{\varphi}(x)
)

Summary statistics

t = f_{\varphi}(x)
x
\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto
\theta
f
\mathcal{N}

 Simulator

Summary statistics

t = f_{\varphi}(x)
x
p_{\Phi}(\theta | f_{\varphi}(x))

Outline

\theta
f
\mathcal{N}

 Simulator

Summary statistics

t = f_{\varphi}(x)
x
p_{\Phi}(\theta | f_{\varphi}(x))

1. Focus on optimal compression

Outline

\theta
f
\mathcal{N}

 Simulator

Summary statistics

t = f_{\varphi}(x)
x
p_{\Phi}(\theta | f_{\varphi}(x))

1. Focus on optimal compression

2. Focus on optimal and simulation-efficient inference

Outline

Optimal Neural Summarisation for Full-Field Cosmological Implicit Inference

Denise Lanzieri, Justine Zeghal

T. Lucas Makinen, Alexandre Boucaud, François Lanusse, and Jean-Luc Starck

x

How to extract all the information?

It is only a matter of the loss function you use to train your compressor..

t = f_{\varphi}(x)
\text{A statistic } t \text{ is said to be sufficient for the parameters } \theta \text{ if }
\text{Sufficient statistic}
p(\theta \: | \: x) = p(\theta \: | \: t) \: \text{ with } \: t=f(x)

We developed a fast and differentiable (JAX) log-normal mass maps simulator

For our benchmark: a Differentiable Mass Maps Simulator

sbi_lens

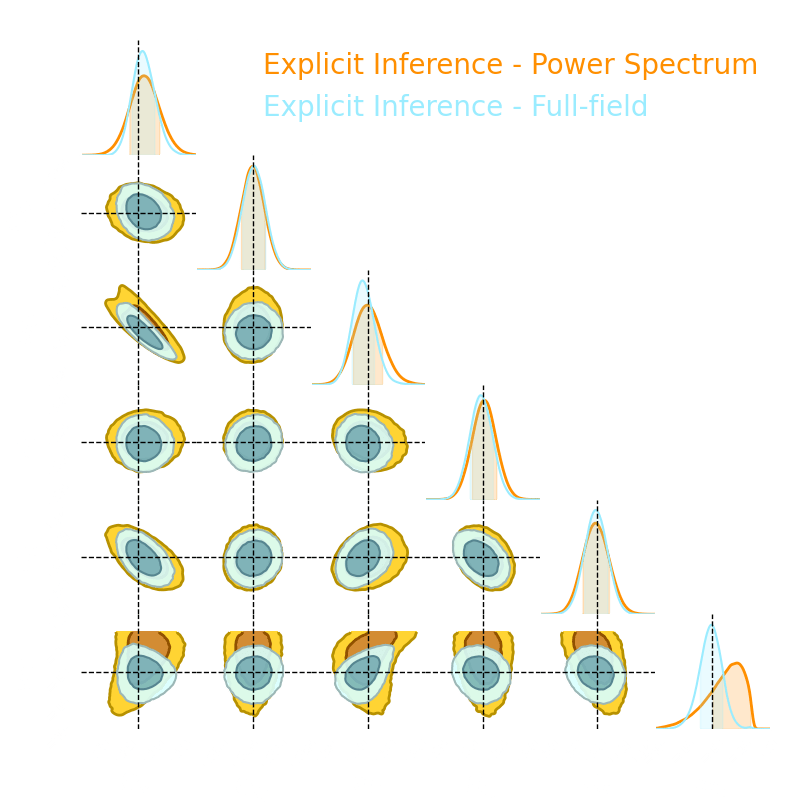
Numerical results

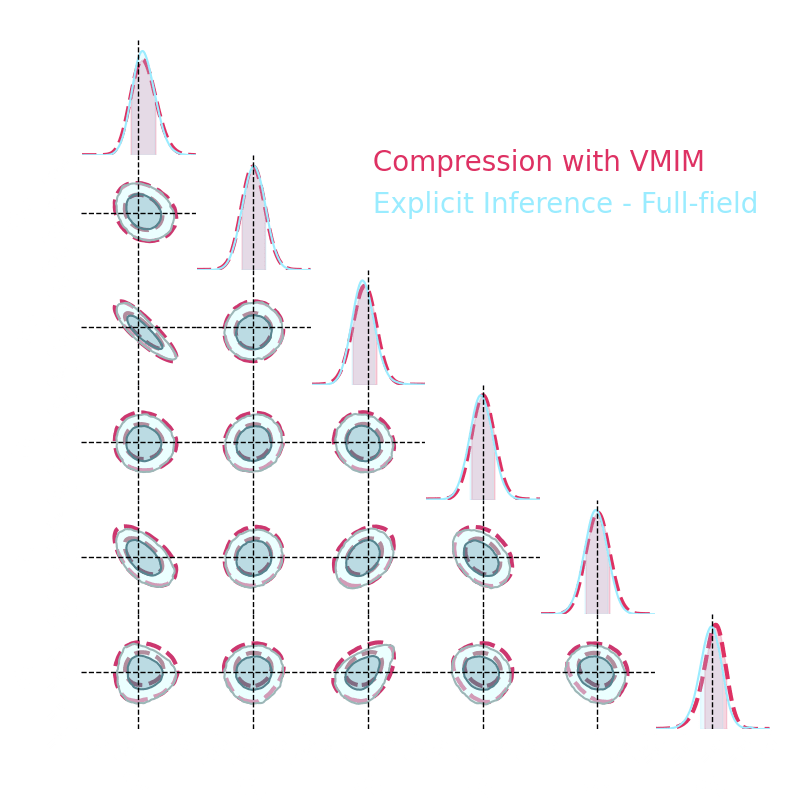
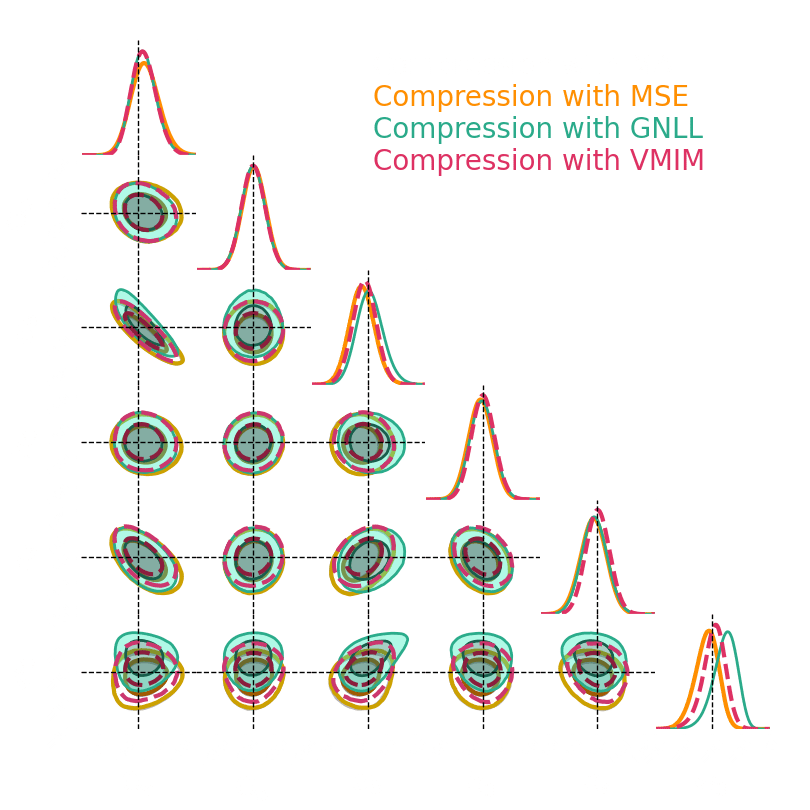
1. We compress using one of the 5 losses.

Benchmark procedure:

2. We compare their extraction power by comparing their posteriors.

For this, we use a neural-based likelihood-free approach, which is fixed for all the compression strategies.

p(\theta \: | \: x) = p(\theta \: | \: t) \: \text{ with } \: t=f(x)
\theta
f
\mathcal{N}

 Simulator

Summary statistics

t = f_{\varphi}(x)
x
p_{\Phi}(\theta | f_{\varphi}(x))

1. Focus on optimal compression

2. Focus on optimal and simulation-efficient inference

Outline

Simulation-Efficient Implicit Inference.

Is differentiability useful?

Justine Zeghal

 Denise Lanzieri, Alexandre Boucaud, François Lanusse, and Eric Aubourg

  • do gradients help implicit inference methods?

In the case of weak lensing analysis,

  • which inference method requires the fewest simulations?

sbi_lens

Log-normal LSST Y10 like

differentiable

simulator

For our benchmark

  • do gradients help implicit inference methods?

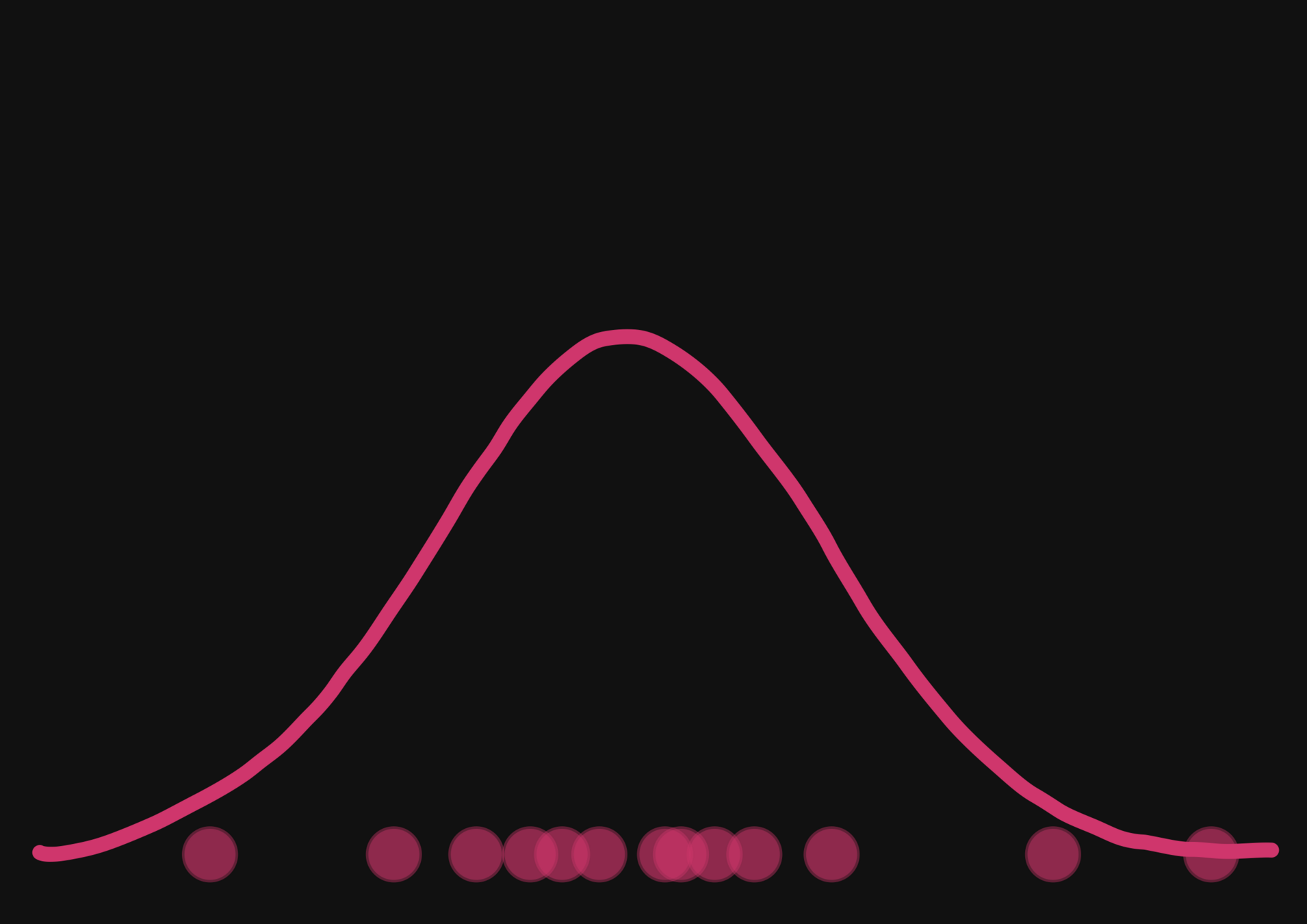
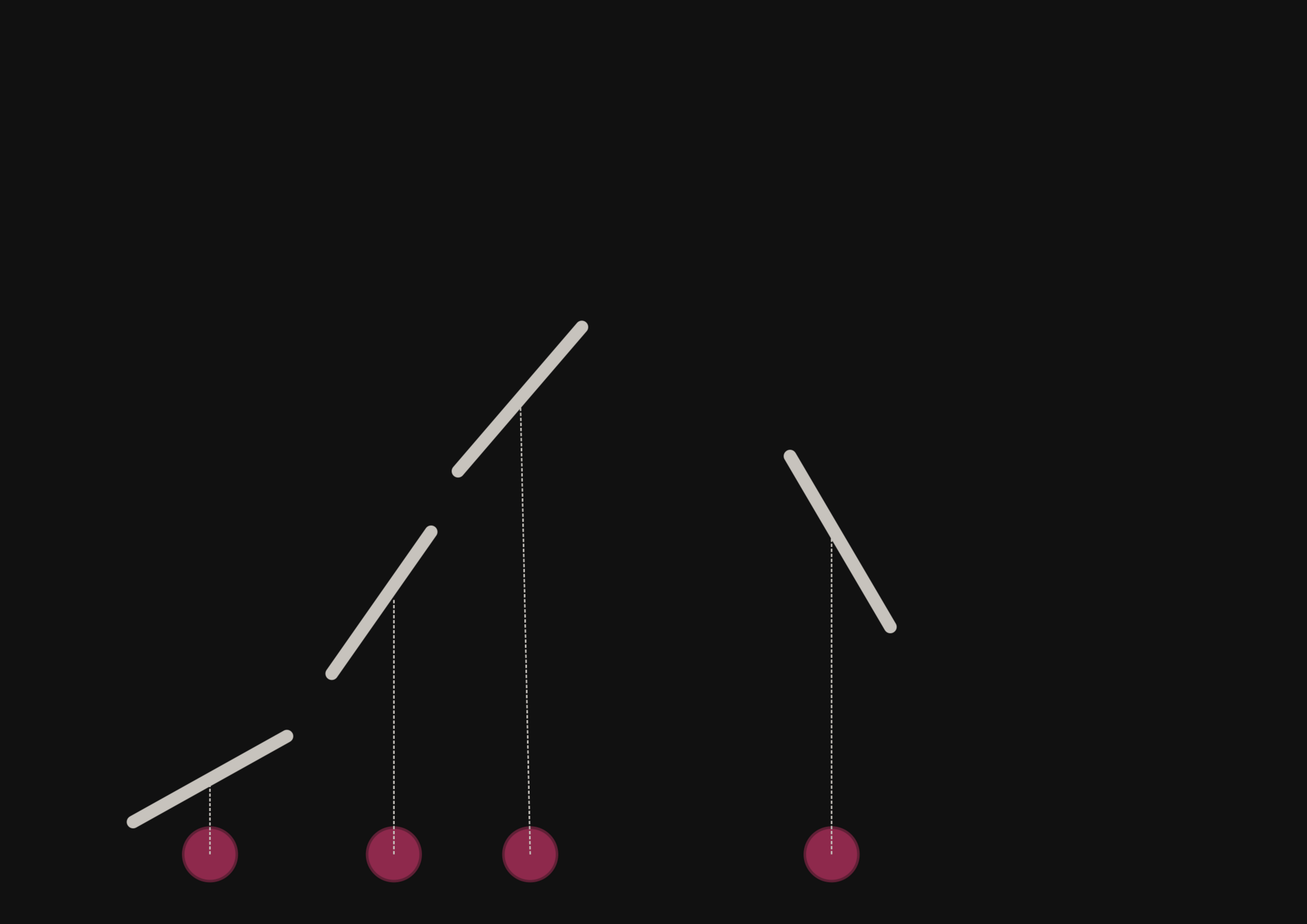
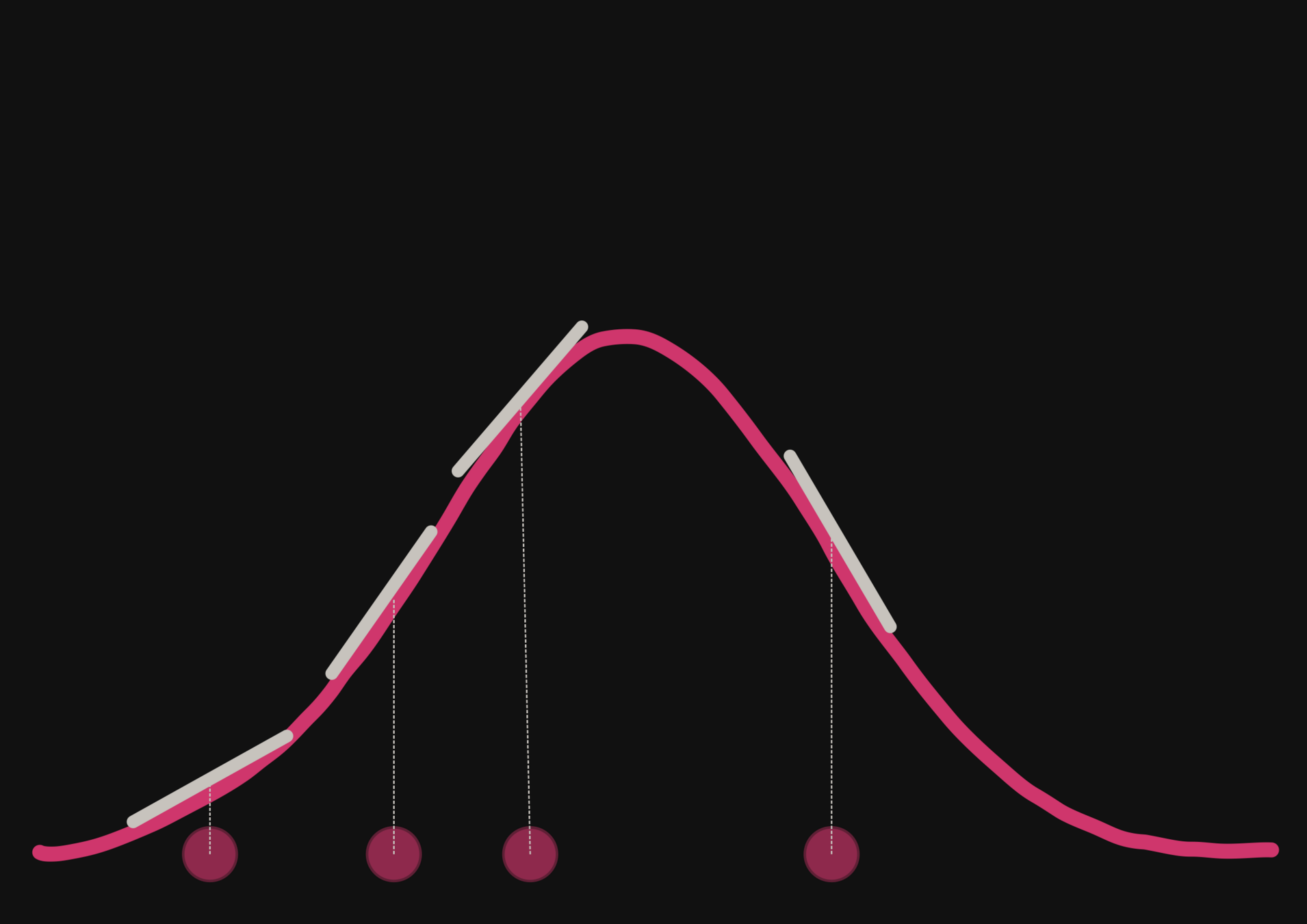
With a few simulations it's hard to approximate the posterior distribution.

→ we need more simulations

BUT if we have a few simulations

and the gradients

 

(also know as the score)

\nabla_{\theta} \log p(\theta | x)

then it's possible to have an idea of the shape of the distribution.

  • do gradients help implicit inference methods?

Normalizing flows are trained by minimizing the negative log likelihood:

  • do gradients help implicit inference methods?

- \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
- \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

Normalizing flows are trained by minimizing the negative log likelihood:

  • do gradients help implicit inference methods?

But to train the NF, we want to use both simulations and gradients

    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

    Normalizing flows are trained by minimizing the negative log likelihood:

    • do gradients help implicit inference methods?

    But to train the NF, we want to use both simulations and gradients

    + \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{\theta} \log p(\theta, z |x) - \underbrace{\nabla_{\theta} \log p^{\phi}(\theta |x)}\parallel_2^2 \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

    Normalizing flows are trained by minimizing the negative log likelihood:

    • do gradients help implicit inference methods?

    But to train the NF, we want to use both simulations and gradients

    + \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{\theta} \log p(\theta, z |x) - \underbrace{\nabla_{\theta} \log p^{\phi}(\theta |x)}\parallel_2^2 \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

    Normalizing flows are trained by minimizing the negative log likelihood:

    • do gradients help implicit inference methods?

    Problem: the gradient of current NFs lack expressivity

    But to train the NF, we want to use both simulations and gradients

    + \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{\theta} \log p(\theta, z |x) - \underbrace{\nabla_{\theta} \log p^{\phi}(\theta |x)}\parallel_2^2 \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

    Normalizing flows are trained by minimizing the negative log likelihood:

    • do gradients help implicit inference methods?

    Problem: the gradient of current NFs lack expressivity

    But to train the NF, we want to use both simulations and gradients

    + \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{\theta} \log p(\theta,z |x) - \underbrace{\nabla_{\theta} \log p^{\phi}(\theta |x)}\parallel_2^2 \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

    Normalizing flows are trained by minimizing the negative log likelihood:

    • do gradients help implicit inference methods?

    Problem: the gradient of current NFs lack expressivity

    But to train the NF, we want to use both simulations and gradients

    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
    + \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{\theta} \log p(\theta,z |x) - \underbrace{\nabla_{\theta} \log p^{\phi}(\theta |x)}\parallel_2^2 \right]

    Normalizing flows are trained by minimizing the negative log likelihood:

    • do gradients help implicit inference methods?

    Problem: the gradient of current NFs lack expressivity

    But to train the NF, we want to use both simulations and gradients

    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
    + \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{\theta} \log p(\theta,z |x) - \underbrace{\nabla_{\theta} \log p^{\phi}(\theta |x)}\parallel_2^2 \right]

    Normalizing flows are trained by minimizing the negative log likelihood:

    • do gradients help implicit inference methods?

    Problem: the gradient of current NFs lack expressivity

    But to train the NF, we want to use both simulations and gradients

    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
    - \mathbb{E}_{p(x)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]
    + \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{\theta} \log p(\theta,z |x) - \underbrace{\nabla_{\theta} \log p^{\phi}(\theta |x)}\parallel_2^2 \right]

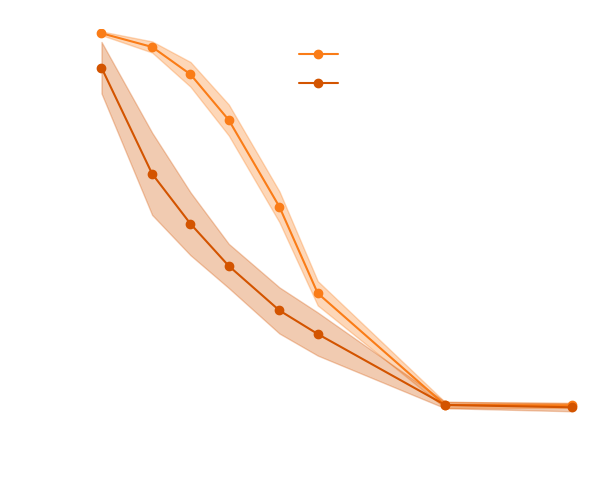
    → On our toy Lotka Volterra model, the gradients helps to constrain the distribution shape

    Zeghal, Lanusse, Boucaud et al., 2022

    • do gradients help implicit inference methods?

    \nabla_{\theta}\log p(x|\theta)
    \nabla_{\theta}\log p(x,z|\theta)

    (from the simulator)

    (requires a lot of additional simulations)

    →For this particular problem, the gradients from the simulator are too noisy to help.

    • do gradients help implicit inference methods?     ~ LSST Weak Lensing case

    • do gradients help implicit inference methods?

    In the case of weak lensing analysis,

    • which inference method requires the fewest simulations?

    sbi_lens

    Log-normal LSST Y10 like

    differentiable

    simulator

    For our benchmark

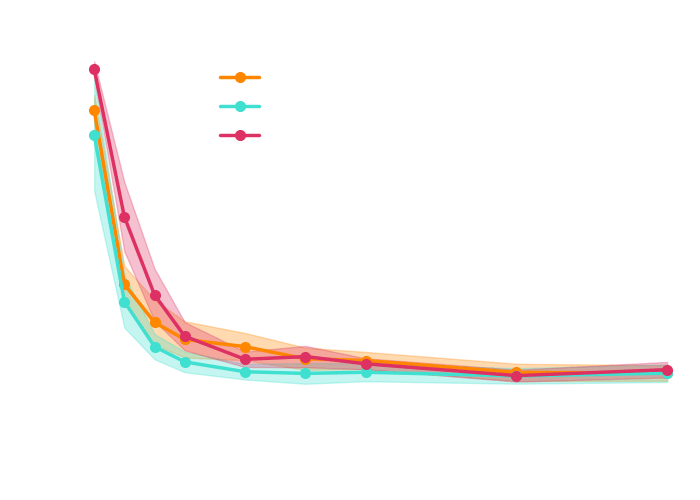
    • which inference method requires the fewest simulation?

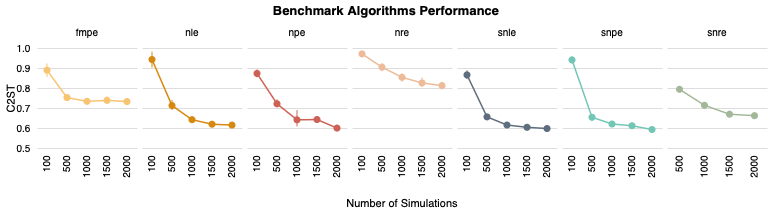
    Focus on implicit inference methods

    • which inference method requires the fewest simulation?

     simulations

     simulations

    10^6
    1000

    more than

    \theta
    f
    \mathcal{N}

     Simulator

    Summary statistics

    t = f_{\varphi}(x)
    x
    p_{\Phi}(\theta | f_{\varphi}(x))

    Thank your for your attention!

    contact: zeghal@apc.in2p3.fr
    slides at: https://slides.com/justinezgh