Kinematics of a Delta Robot in CGA

Hugo Hadfield

November 2019

hh409.user.srcf.net

Delta Robots

  • Very fast moving
  • Simple forward and inverse kinematics
  • Cheap and easy to build

History of the Delta Robot

  • Invented by Reymond Clavel at EPFL in 1985
  • A type of parallel manipulator

Model of a Delta Robot

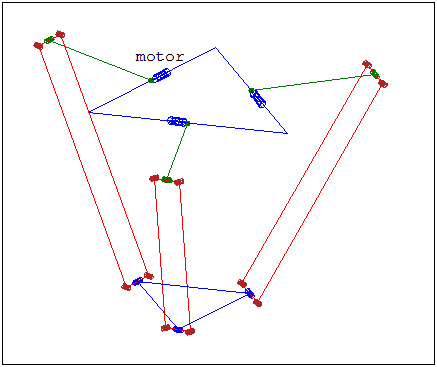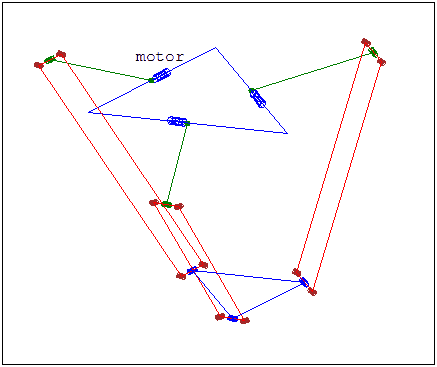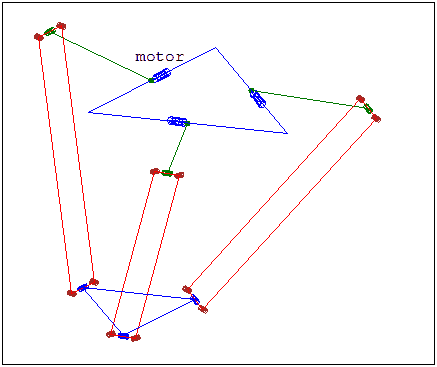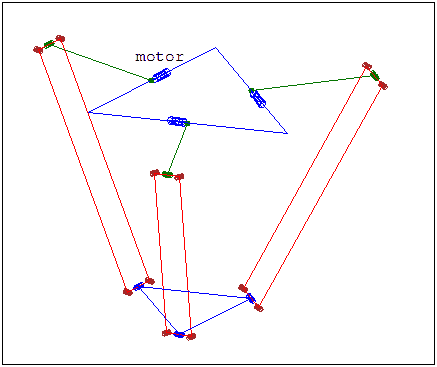
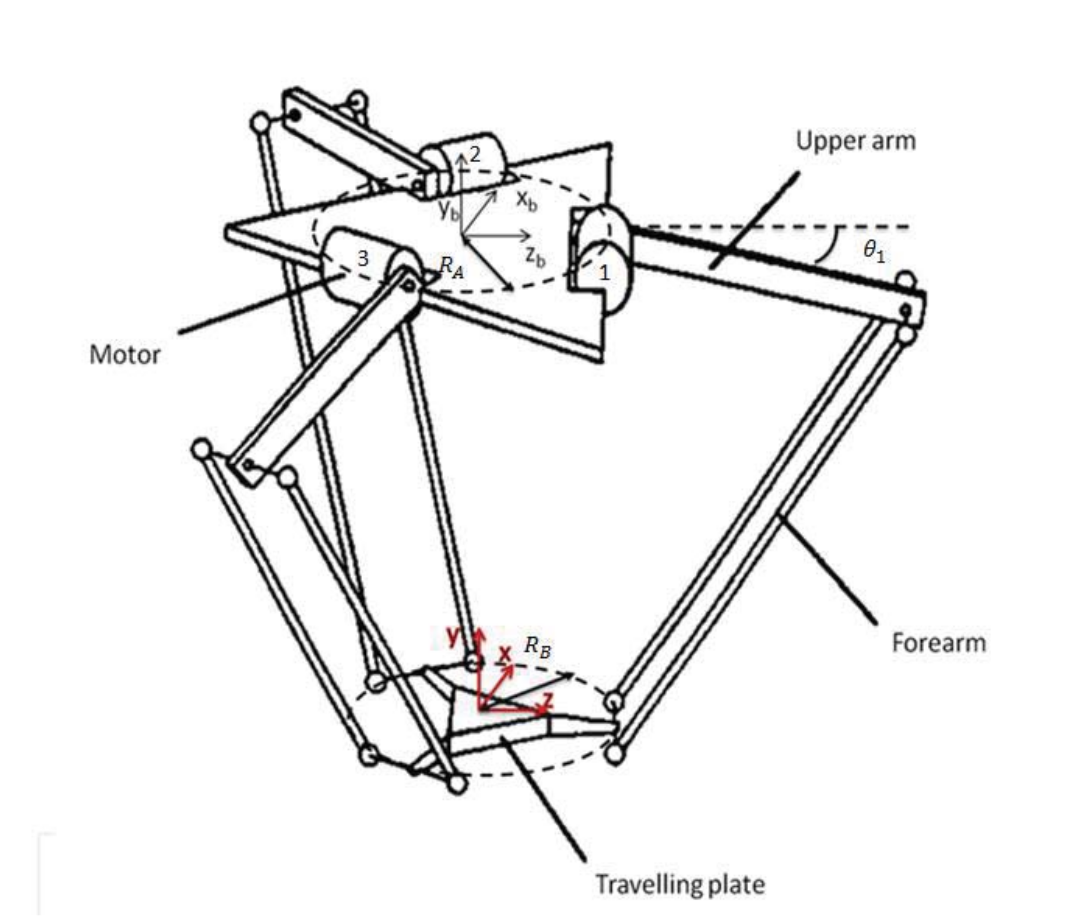
Forward Kinematics

\begin{aligned} a_i &= (r_b - r_e + l\cos(\theta_i))s_i + l\sin(\theta_i)e_3\\ A_i &= \frac{1}{2}a_i^2n_\infty + a_i - n_0\\ \Sigma_i &= A_i - \frac{1}{2}\rho^2n_\infty\\ T &= I_5\bigwedge_{i=0}^{i=2}\Sigma_i\\ P &= 1 + \frac{T}{\sqrt{T^2}}\\ Y &= -\tilde{P}(T\cdot n_\infty)P\\ y &= \frac{-\sum_{j=1}^{j=3}(Y\cdot e_j)e_j}{Y\cdot n_\infty} \end{aligned}
r_e
Y
A_i
r_b
l
\rho
\theta

Reachable Volume

Inverse Kinematics

\begin{aligned} C_i &= \left( \text{up}(r_bs_i) - \frac{1}{2}l^2n_\infty \right)\wedge(I_3s_i\wedge e_3) \\ \Sigma_i &= \text{up}(y + r_es_i) - \frac{1}{2}\rho^2n_\infty \\ T_i &= (C_i\wedge\Sigma_i)I_5\\ P_i &= \frac{1}{2}(1 + \frac{T_i}{\sqrt{T_i^2}})\\ A_i &= -\tilde{P_i}(T_i\cdot n_\infty)P_i\\ a_i &= -\frac{\sum_{j=1}^{j=3}(A_i\cdot e_j )e_j}{A_i\cdot n_\infty} \\ z_i &= a_i - r_bs_i \\ \theta_i &= \arctan{\frac{z_i\cdot e_3}{z_i\cdot s_i}} \end{aligned}

If \(T_i^2 < 0\) then the point is unreachable

Forward Jacobian

- Move only one motor

 

- This fixes two of the spheres, they intersect in a circle

 

- We are therefore interested in the differential of the end point of the point pair made from intersection of the circle and the moving sphere

- First we need to find how the center of the sphere changes as we move theta

\Sigma_i = A_i - \frac{1}{2}\rho^2n_\infty \\

- How does point pair move with the sphere?

= \frac{\partial \Sigma_i}{\partial \theta_i} = \frac{\partial A_i}{\partial \theta_i} = -(r_b - r_e)l\sin(\theta_i)n_\infty - l\sin(\theta_i)s_i + l\cos(\theta_i)e_3
= \left( \frac{\partial a_i}{ \partial \alpha}\cdot a_i \right)n_\infty + \frac{\partial a_i}{\partial \alpha}
\frac{\partial \Sigma_i}{\partial \alpha} = \frac{\partial A_i}{\partial \alpha} = \frac{1}{2}\frac{\partial a_i^2}{\partial \alpha}n_\infty + \frac{\partial a_i}{\partial \alpha} \\

Forward Jacobian (2)

T = \Sigma_i\wedge C\\ \frac{\partial T }{\partial \theta_i} = \frac{\partial \Sigma }{\partial \theta_i}\wedge C\\

- Now we need to know how the conformal endpoint of the point pair changes

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } P = \frac{1}{2}\left(1 + \frac{T}{\sqrt{T^2}}\right)\\ Y = -\tilde{P}(T\cdot n_\infty)P\\ \pdiff{P}{\theta_i} = \frac{1}{2T^2}\left(\sqrt{T^2}\pdiff{T}{\theta_i} - T\frac{\pdiff{T}{\theta_i}\cdot T}{\sqrt{T^2}}\right)\\ \pdiff{Y}{\theta_i} = -\tilde{\pdiff{P}{\theta_i}}(T\cdot n_\infty)P -\tilde{P}(\pdiff{T}{\theta_i}\cdot n_\infty)P -\tilde{P}(T\cdot n_\infty)\pdiff{P}{\theta_i}

- How does the 3D endpoint change with the conformal endpoint change? (derivative of 'down' function)

Forward Jacobian (3)

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \pdiff{y}{\theta_i} = \frac{ -\sum_{j=1}^{j=3}\left(\pdiff{Y}{\theta_i}\cdot e_{j}\right)e_j (Y\cdot\ninf) + \sum_{j=1}^{j=3}\left(Y\cdot e_{j}\right)e_j (\pdiff{Y}{\theta_i}\cdot\ninf) }{ (Y\cdot\ninf)^2 }
\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } y = \frac{-\sum_{j=1}^{j=3}(Y\cdot e_j)e_j}{Y\cdot n_\infty}

- We now have a closed form expression for the derivative of the endpoint wrt. theta and we didn't have to use maple once!

- We can use this for control and optimisation. Consider a cost function:

Forward Jacobian In Use

g(y) = (y-t)^2 \\ \frac{\partial g}{\partial \theta_i} = 2\frac{\partial y}{\partial \theta_i}\cdot(y-t)

- We therefore have a closed form for

and so can do gradient descent

\nabla g

- Given the forward jacobian we can simply invert the 3x3 matrix at each point to get the inverse jacobian

OR

- We can differentiate our inverse kinematic equations..

Inverse Jacobian

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \begin{aligned} \Sigma_i &= X_i - \frac{1}{2}\rho^2n_\infty \\ \frac{\partial \Sigma_i}{\partial \alpha} &= \frac{\partial X_i}{\partial \alpha} = \left(\pdiff{x_i}{\alpha}\cdot x_i\right) \ninf + \pdiff{x_i}{\alpha}\\ x_i &= y + r_es_i\\ \frac{\partial x_i}{\partial \alpha} &= \frac{\partial y}{\partial \alpha} \end{aligned}

Starting with Sigma_i

Differentiate wrt. a scalar param \alpha

the sphere centred at the meeting of the 4 bar mechanism and the end platform

- Now we need to know how the elbow positions vary with \alpha

Inverse Jacobian (2)

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \begin{aligned} C_i &= \left( B_i - \frac{1}{2}l^2n_\infty \right)\wedge(I_3s_i\wedge e_3)\\ T_i &= (\Sigma_i\wedge C_i)^*\\ \pdiff{T_i}{\alpha} &= (\pdiff{\Sigma_i}{\alpha}\wedge C_i)^* \end{aligned}

- Here A_i is the conformal elbow position

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \begin{aligned} \pdiff{A_i}{\alpha} &= -\tilde{\pdiff{P_i}{\alpha}}(T_i\cdot n_\infty)P_i -\tilde{P_i}(\pdiff{T_i}{\alpha}\cdot n_\infty)P_i -\tilde{P_i}(T_i\cdot n_\infty)\pdiff{P_i}{\alpha}\\ \pdiff{a_i}{\alpha} &= \frac{ -\sum_{j=1}^{j=3}\left(\pdiff{A_i}{\alpha}\cdot e_{j}\right)e_j (A_i\cdot\ninf) + \sum_{j=1}^{j=3}\left(A_i\cdot e_{j}\right)e_j (\pdiff{A_i}{\alpha}\cdot\ninf) }{ (A_i\cdot\ninf)^2 } \end{aligned}

- Finally we need to know how the joints vary with elbow position

Inverse Jacobian (3)

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \begin{aligned} z_i &= a_i - r_bs_i \\ \theta_i &= \arctan{\frac{z_i\cdot e_3}{z_i\cdot s_i}}\\ \frac{\partial \theta_i}{\partial \alpha} &= \frac{z_i\cdot s_i \frac{\partial z_i}{\partial \alpha}\cdot e_3 - z_i\cdot e_3 \frac{\partial z_i}{\partial \alpha}\cdot s_i}{z_i^2} \end{aligned}

- We are done (Once again no Maple!)

- The inverse jacobian allows us to map velocity of the endpoint to velocity of joints

Inverse Jacobian in Use

g(y) = (y - t)^2 \\ \frac{\partial g}{\partial y} = 2(y-t)\\

- In other words, to minimise cost at maximum rate drive the end point linearly at our target point (obviously)

- With the inverse jacobian we can do exactly that

\newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\nn}{\nonumber} \newcommand{\ninf}{n_{\infty}} \newcommand{\einf}{e_{\infty}} \newcommand{\no}{n_{0}} \newcommand{\eo}{e_{0}} \newcommand{\wdg}{\wedge} \newcommand{\pdiff}[2]{\frac{\partial #1}{\partial #2} } \begin{aligned} \pdiff{y}{\alpha_j} \propto (2(t-y))\cdot e_j \end{aligned}

- CGA provides a very neat framework for solving the forward and inverse kinematics of parallel robots

 

- We can easily simulate the dynamics of the robot with clifford and ganja.js

Summary

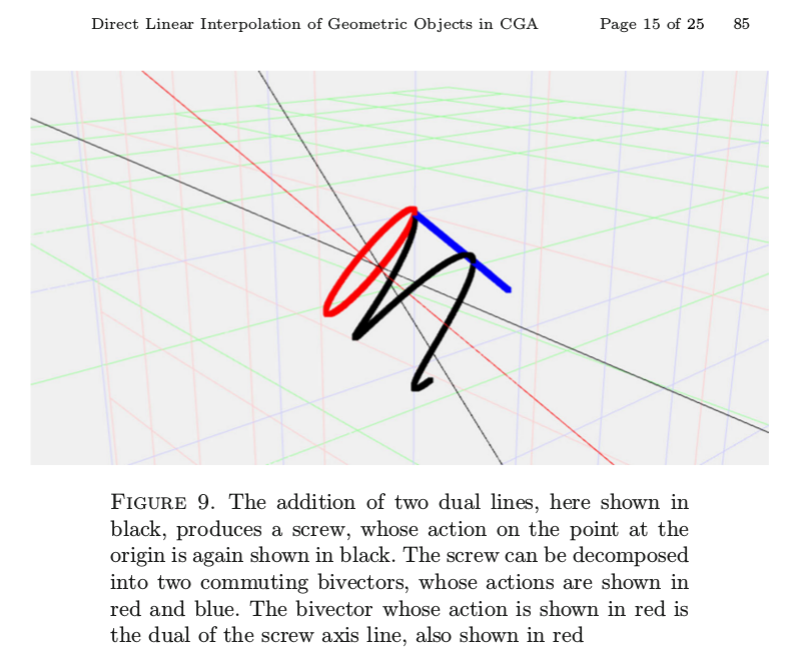
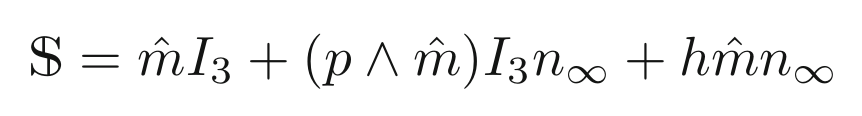
https://link.springer.com/article/10.1007/s00006-019-1003-y

- Trivectors in CGA represent lines and circles

 

- The direct interpolation of lines and circles results in trivectors interpretable as general screws

- Screw theory is widely used in robotics for analysis of kinematics and dynamics

 

- Lets bring screw theory and CGA (also PGA) together properly and analyse a whole load of systems

Future Work